Nicolas Bacaër
Institut de recherche pour le développement
32 avenue Henri Varagnat, 93143 Bondy cedex, France
nicolas.bacaer@ird.fr
Cet article présente le lien entre le choix d'une rotation culturale tenant compte de « l'effet précédent » et des modèles mathématiques relevant de la théorie des graphes. Dans un premier modèle, le revenu de l'année n dépend seulement des cultures des années n et n-1 . Dans un deuxième modèle, le revenu de l'année n dépend des cultures des années n, n-1 et n-2. Le problème est de choisir une rotation culturale qui optimise le revenu annuel moyen.
Des modèles mathématiques pour l'optimisation des systèmes de culture ont été introduits dans les années 1960 par des économistes. Ils ont formulé plusieurs problèmes traditionnels, par exemple le choix du pourcentage de la surface agricole à attribuer aux différentes cultures, comme des problèmes de « programmation linéaire », une théorie mathématique développée par Dantzig (1963). La théorie s'accompagne d'un algorithme appelé « méthode du simplexe » qui nécessite l'usage d'un ordinateur. Des applications agricoles se trouvent par exemple dans le livre de Boussard et Daudin (1988). Un logiciel destiné aux agriculteurs a été développé par le CEMAGREF (1992).
Dans ces références, le problème du choix de la rotation culturale est insuffisamment étudié. On présente donc dans cet article des modèles mathématiques pour l'optimisation de ces rotations culturales tenant compte essentiellement de « l'effet précédent ». Aux rotations culturales correspondent des cycles dans des graphes mathématiques. Jusqu'à présent, ils étaient étudiés en vue d'applications très différentes : problèmes de transport, problèmes d'automatique dans des chaînes de montage (Baccelli et coll. 1992), etc. Il existe un algorithme très efficace pour résoudre ces problèmes, appelé algorithme de Howard, qui est d'ailleurs implémenté dans un logiciel de l'INRIA.
Considérons un agriculteur qui veut cultiver une parcelle, et pour laquelle il peut choisir chaque année entre P cultures différentes : blé, orge, navet, jachère, etc. Supposons que le revenu de l'année n dépende seulement des cultures des années n et n-1 . \(\,x_n\,\) est la culture de l'année n. \(\,K(x_{n-1},x_n)\,\) est le revenu de l'année n. Considérons maintenant un graphe à P nœuds, chaque nœud correspondant à une culture, avec des arêtes orientées reliant tous les nœuds entre eux (y compris les arêtes reliant un nœud à lui-même). À la arête qui va du nœud i au nœud j est associé un poids : \(\,K(i,j)\). Une rotation culturale, c'est-à-dire une suite périodique de cultures, correspond alors à un cycle dans le graphe mathématique. La meilleure rotation culturale sera alors celle qui optimise le revenu annuel moyen \[ \frac{ K(x_0,x_1) + K(x_1,x_2) + \ldots + K(x_{L-1},x_0) }{L}. \] On se rend compte assez facilement qu'il suffit de se restreindre aux cycles élémentaires, c'est-à-dire à ceux qui ne passent pas deux fois par le même nœud. Les autres cycles sont en fait composés de cycles élémentaires et ne peuvent pas engendrer un revenu annuel moyen supérieur. Cette propriété montre déjà les limites de ce modèle, car en pratique, de nombreuses rotations culturales contiennent plusieurs fois la même culture. Dans la région du Noyonnais en France par exemple, une douzaine de rotations culturales différentes ont été recensées (Sébillotte, 1989). Certaines, telle la rotation culturale betterave - pomme de terre - blé, sont compatibles avec notre premier modèle. D'autres, telle la rotation culturale betterave - blé - blé, ne le sont pas. Cette critique sera levée dans le deuxième modèle.
Revenons au premier modèle. Une manière de trouver la rotation culturale optimale est de faire la liste de toutes les rotations culturales élémentaires. \(\,P(P-1)\ldots (P-L+1)/L\,\) rotations culturales sont de longueur L, avec 1≤L≤P. Pour P=3 cultures, il y a
ftp.inria.fr/INRIA/Projects/Meta2/Scilab/contrib/MAXPLUS.L'algorithme est utilisable au sein du logiciel scilab
http://www-rocq.inria.fr/scilab.La théorie montre que R ne peut prendre qu'une valeur bien déterminée, qui est en fait le revenu annuel moyen maximal. On choisit ensuite pour chaque \(\,i=1\ldots P\) un nombre \(j=c(i)\). Ce nombre donne le maximum dans le membre de gauche de l'équation numéro i ci-dessus. Pour obtenir une rotation culturale optimale, on choisit un quelconque \(\,x_0\,\), puis on prend par récurrence \(x_n=c(x_{n-1})\). La suite devient périodique au bout de quelques itérations, et la rotation culturale obtenue est optimale.
\(u(1)\), \(\ldots\), \(u(P)\,\) sont des nombres qui ont une interprétation. Ils forment un système de prix pour l'achat et la vente de la parcelle. Si la culture \(\,i\) a été cultivée juste avant la transaction, alors \(u(i)\,\) est le juste prix de cette transaction. On effet, ce système de prix assure que le revenu annuel moyen maximal reste le même d'un exploitant à l'autre. Autrement dit, le revenu sur n années tenant compte de l'achat \(\,-u(x_0)\) et de la vente \(+u(x_n)\), \[ \frac{ \max_{x_1, \ldots, x_n} \{ K(x_0,x_1) + K(x_1,x_2) +\ldots + K(x_{n-1},x_n) + u(x_n) \} - u(x_0) }{n},\] est indépendant de \(x_0\,\) et de n. Signalons enfin le lien avec le problème de l'assolement et la programmation linéaire. Supposons que la parcelle puisse être divisée pour accueillir différentes cultures. \(r_n(i,j)\,\) est le pourcentage de la surface cultivé avec j l'année n et avec i l'année n-1 . On suppose que \(\,x_0\), \(x_1\), \(\ldots\), \(x_{L-1}\,\) est une rotation culturale optimale. On peut montrer que le revenu annuel moyen maximal R peut aussi être obtenu en choisissant chaque année \(\,r_n(i,j)=r(i,j)=1/L\) si \(i=x_{k-1}\) et \(j=x_k\,\) pour une valeur de k (avec \(\,x_L=x_0\)), c'est-à-dire en découpant la parcelle en L plus petites parcelles de même surface accueillant les cultures de la rotation culturale optimale. Par conséquent, R est aussi la valeur du problème de programmation linéaire \[ \max \sum_{i,j} K(i,j) r(i,j)\] avec les contraintes \[r(i,j)\geq 0, \quad \sum_i \sum_j r(i,j)=1, \quad \sum_j r(j,i)=\sum_j r(i,j).\]
Supposons maintenant que le revenu de l'année n dépende des cultures des années n, n-1 et n-2 . \(K(x_{n-2},x_{n-1},x_n)\,\) est le revenu de l'année n. Considérons un graphe mathématique avec \(\,P^2\,\) nœuds. Chaque nœud correspond à deux cultures. Ce couple représente les cultures de deux années consécutives. Les arêtes ne relient que les nœuds tels que la seconde culture du nœud de départ soit la même que la première culture du nœud d'arrivée. Si la arête va de (i,j) à (j,k), alors son poids est \(\,K(i,j,k)\). Une rotation culturale, c'est-à-dire une suite périodique de cultures, correspond alors à un cycle dans le graphe mathématique. La meilleure rotation culturale sera alors celle qui optimise le revenu annuel moyen. On se rend compte comme dans le premier modèle qu'il suffit de se restreindre aux cycles élémentaires, c'est-à-dire à ceux qui ne passent pas deux fois par le même nœud.
Prenons par exemple P=2. Il y a 4 nœuds : (1,1), (1,2), (2,1), (2,2). Partant de (1,1), il y a 2 arêtes :
Contrairement au premier modèle, il est assez difficile de compter le nombre de cycles élémentaires. Avec P=2, il y en a 6, qui sont 1, 2, 1-2, 1-1-2, 1-2-2 et 1-1-2-2. Avec P=3, il y en a 148. Avec P=4, il y en a 120538. Ce nombre croît extrêmement vite. Nous avons utilisé un programme informatique basé sur l'algorithme de Tiernan (1970) pour les compter. Pour obtenir une rotation culturale optimale, on doit utiliser l'algorithme de Howard pour une équation du même type que l'équation (1), mais légèrement plus compliquée.
On prend P=2, avec 1 représentant la jachère et 2 représentant une céréale. Supposons que le revenu K puisse être décomposé en \[K(x_{n-2},x_{n-1},x_n) = b(x_{n-2})\, a(x_{n-1})\, Q(x_n).\] \(Q(x_n)\) représente une sorte de revenu maximum théorique associé à la culture \(x_n\). Les deux nombres \(\,a(x_{n-1})\) et \(b(x_{n-2})\,\) sont compris entre 0 et 1 et représentent l'effet précédent et l'effet avant-dernier.
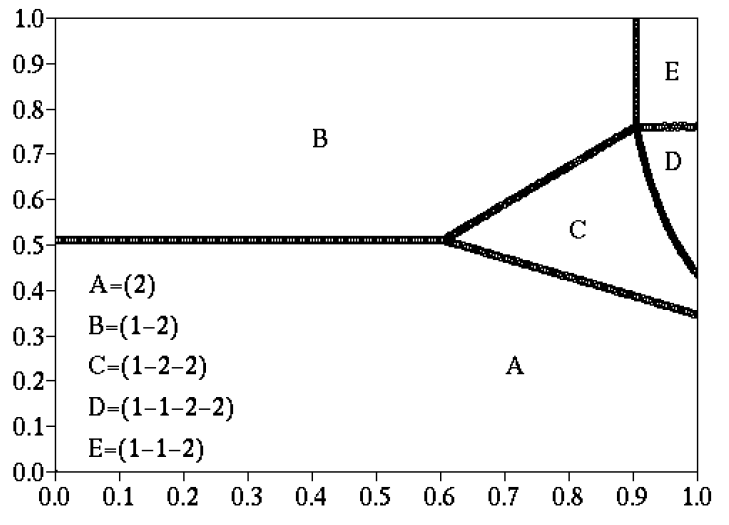
Comme exemple numérique, on a pris \(\,Q(1)=0\), comme il se doit pour une jachère, \(R(2)=20\) (l'unité importe peu ici), \(a(2)=\mbox{0,25}\) (la céréale épuise le sol) et \(b(2)=\mbox{0,6}\,\). Ces valeurs peuvent être critiquées. On laisse les deux paramètres \(\,a(1)\) et \(b(1)\,\) varier entre 0 et 1. En effet, la fertilité du sol après la jachère dépend beaucoup du travail de l'agriculteur. Dans l'antiquité et durant le moyen-âge (Mazoyer et coll. 1997), ce n'était que pendant la période de jachère que la fertilisation avec les excréments du bétail était possible. Si on augmente les deux paramètres, la solution optimale de l'antiquité (céréale-jachère) est remplacée par la solution optimale du moyen-âge (jachère-céréale-céréale). La figure montre le résultat des calculs. L'axe vertical représente \(\,a(1)\,\), l'axe horizontal \(b(1)\). Pour chaque valeur de \(a(1)\) et \(b(1)\,\) entre 0 et 1, on calcule la rotation culturale optimale avec l'algorithme de Howard. Pour de grandes zones dans le diagramme, cette rotation culturale est la même ; c'est pourquoi dans notre programme, on se contente de rechercher la limite de ces zones par une méthode de dichotomie.
On peut voir sur la figure que la transition de systèmes de culture au moyen-âge
correspond au passage de la zone B à la zone C. Dans le cadre de ce modèle et vu
la figure, il semble que la transition soit due à un accroissement de \(b(1)\) plus que de
\(a(1)\). Cela signifie que la contribution principale n'est pas l'effet précédent mais l'effet avant-dernier. D'ailleurs, remarquons que dans le cadre du premier modèle (qui ne
tient compte que de l'effet précédent), on ne peut pas expliquer la transition. En effet,
distinguons une céréale de printemps 2 et une céréale d'hiver 3, parce qu'il
faut au moins 3 cultures dans le premier modèle pour avoir une rotation culturale optimale
triennale. Il n'est pas possible qu'en augmentant \(\,K(1,2)\) et \(K(1,3)\), le revenu moyen
\((K(1,2)+K(2,3))/3\) devienne supérieur à \(K(1,2)/2\).
