Mathematical Population Studies 10 (2003) 1-20
Nicolas Bacaër
L'objectif de cet article est de discuter de l'influence de l'immigration dans un modèle mathématique pour l'évolution de la structure par âge de la population. Dans le cas sous-critique, la structure par âge converge vers un état stationnaire. On présente un programme qui simule le modèle et qui est utilisé pour des projections pour la population de la France. On insiste aussi sur le lien avec un modèle plus complexe.
Mots clés : démographie, structure de la population, immigration, équations aux dérivées partielles, transformation de LaplaceOn divise une population en K sous-populations (\(K\geq 1\)). Les variables x et t représentent l'âge et le temps.
Ces résultats sont démontrés dans la section 2. L'étude du comportement asymptotique de \(\,P(x,t)\) revient à celle d'une équation intégrale \[\Phi(t)=F(t)+\int_0^t G(x) \Phi(t-x)\, dx,\quad t > 0.\] \(F(t)\) et \(G(x)\,\) sont des fonctions connues. Ce problème a été étudié par Lotka (1939) dans le cas d'une équation (\(K=1\)). Pour un système d'équations (K>1), Bellman et Cooke (1963) ont étudié le cas où \(\,\int_0^\infty G(x)\, dx\,\) est une matrice irréductible (au sens de la théorie de Perron et Frobenius des matrices positives). Crump (1970 et 1971) a étudié le cas réductible. Ces études se sont focalisées sur le cas où \(\,F(t)\to 0\) si \(t \to \infty\). Dans notre modèle, le terme inhomogène de migration dans les équations de McKendrick implique que \(F(t)\) a une limite non nulle si \(t \to \infty\). Si l'on soustrait l'état stationnaire, le problème inhomogène se réduit à un problème homogène, pour lequel on peut appliquer les résultats sur l'existence et le comportement asymptotique. On propose néanmoins ci-dessous une démonstration pour obtenir le second résultat \(\,(P(x,t)\geq 0)\,\) et parce que la démonstration est assez simple avec l'hypothèse sous-critique ρ<1. On n'a pas besoin de distinguer les cas réductibles et irréductibles.
Dans la section 3, on présente trois exemples qui modélisent des populations humaines. Dans chaque exemple, \(M(x)\) représente l'immigration et \(d_k(x)\,\) la mortalité, qui pourrait aussi inclure le taux d'émigration. Dans le troisième exemple, \(\,\tau_{k,l}(x)\,\) représente le taux de changement de nationalité pour les étrangers. La section 4 présente un programme qui simule le modèle et son application aux trois exemples, en utilisant des données de France. Dans la section 5, on fait le lien avec un modèle plus complexe étudié par Arino et Smith (1998). Le modèle plus complexe représente mieux les populations réelles. Cependant, il fait intervenir des paramètres difficiles à estimer par manque de données pour les populations humaines des sections précédentes. La conclusion indique comment le modèle de base (1)-(2)-(3) pourrait s'appliquer à des populations animales. Les équations prennent alors un sens différent.
Pour finir, mentionnons quelques études sur la modélisation de l'immigration. Barbu, Iannelli et Martcheva (2001) ont étudié la contrôlabilité de la structure par âge d'une population par une immigration sélective sur l'âge. Dans le livre d'Alvarado et Creedy (1998), on trouve des modèles discrets.
Le système d'équations aux dérivées partielles linéaires du premier ordre se réduit à un système d'équations différentielles ordinaires linéaires du premier ordre le long des courbes caractéristiques. On a ainsi \begin{equation}\tag{5} P(x,t)=S(x-t,x) P^0(x-t)+\int_{x-t}^x S(u,x) M(u)\, du, \quad \forall x > t, \end{equation} \begin{equation}\tag{6} P(x,t)=S(0,x)P(0,t-x) + \int_0^x S(u,x) M(u)\, du, \quad \forall x < t. \end{equation} On définit \(\,\Phi(t)=P(0,t)\). On a \[\Phi(t)=\int_0^t B(x) P(x,t)\, dx + \int_t^\infty B(x) P(x,t)\, dx,\quad t > 0.\] Il résulte des formules obtenues pour x>t et x<t que \(\,\Phi(x,t)\) est solution d'une équation intégrale \begin{equation}\tag{7} \Phi(t)=F(t)+\int_0^t G(x) \Phi(t-x)\, dx,\quad t > 0. \end{equation} \(G(x)\) est la matrice \[G(x)=B(x) S(0,x).\] \(F(t)\) est le vecteur \begin{align} F(t)=&\int_0^t B(x) \int_0^x S(u,x) M(u)\, du\, dx +\int_t^\infty B(x) S(x-t,x) P^0(x-t)\, dx \nonumber\\ &+\int_t^\infty B(x) \int_{x-t}^x S(u,x) M(u)\, du\, dx. \tag{8} \end{align} L'équation (1) a une unique solution, comme on peut le voir avec la méthode des approximations successives (Bellman et Cooke, 1963). Donc l'équation aux dérivées partielles initiale a aussi une unique solution. Or les éléments sur la diagonale de Δ sont positifs ou nuls et ceux en dehors de la diagonale sont négatifs ou nuls. Ceci implique que si \(\,a\leq b\), \(S(a,b)\,\) est une matrice à coefficients positifs ou nuls (Berman et Plemmons, 1994 chap. 6 §3.12). On a donc \(\,F(t)\geq 0\) et \(G(x)\geq 0\ \forall \, x,t\geq 0\). D'après la méthode des approximations successives, \(\,\Phi(t)\geq 0\ \forall\, t\geq 0\). D'après (5) et (6), \(\,P(x,t)\geq 0\ \forall \, x,t\geq 0\). Ceci démontre les deux premiers résultats.
\(\xi_0(\Phi)\,\) est le plus petit nombre réel tel que l'intégrale vectorielle suivante soit absolument convergente \[\hat{\Phi}(z)=\int_0^\infty e^{-zt} \Phi(t)\, dt, \quad \forall z \in \mathbb{C},\ \mathrm{Re}(z) > \xi_0.\] C'est la transformée de Laplace de Φ. On définit \(\,\xi_0(F)\) et \(\xi_0(G)\) de la même manière. \(B(x)\) est une fonction dont le support est compact. \(G(x)\) est donc aussi une fonction avec un support compact et \(\xi_0(G)=-\infty\). On a donc \[ \hat{\Phi}(z)=\hat{F}(z)+\hat{G}(z) \hat{\Phi}(z), \quad \forall z \in \mathbb{C}, \ \mathrm{Re}(z) > \max \{\xi_0(\Phi),\xi_0(F)\}.\] \(I\,\) est la matrice identité de taille K. On a alors \[(I-\hat{G}(z))\hat{\Phi}(z)=\hat{F}(z).\] On prend \(z\in \mathbb{C}\) avec \(\xi=\mathrm{Re}(z) > 0\). On a \[|\hat{G}_{k,l}(z)| \leq \hat{G}_{k,l}(\xi) \leq \hat{G}_{k,l}(0),\quad \forall 1\leq k,l\leq K.\] D'après Horn et Johnson (1985, §8.1.18 et 8.1.19), on a pour les rayons spectraux correspondants \[\rho(\hat{G}(z)) \leq \rho(\hat{G}(\xi)) \leq \rho(\hat{G}(0)) < 1,\] et \(I- \hat{G}(z)\,\) est inversible. On a ainsi \[\hat{\Phi}(\lambda)=(I-\hat{G}(z))^{-1} \hat{F}(z),\quad \forall z \in \mathbb{C}, \ \mathrm{Re}(z) > \max \{\xi_0(\Phi),\xi_0(F)\}.\] On prend la transformée de Laplace inverse. On obtient pour tout nombre réel \(\,\xi > \max \{\xi_0(\Phi),\xi_0(F),0\}\) et \(\forall t > 0\), \begin{equation}\tag{9} \Phi(t)=\frac{1}{2\pi i} \lim_{\eta \to \infty} \int_{\xi-i\eta}^{\xi+i\eta} e^{zt} (I-\hat{G}(z))^{-1} \hat{F}(z)\, dz. \end{equation} On définit \(X=\sup\{x\geq 0;\ \exists k,l,\ B_{k,l}(x) > 0\}\). La formule (8) donne \[F(t)=L=\int_0^\infty B(x) \int_0^x S(u,x) M(u)\, du\, dx, \quad \forall \, t\geq X.\] Avec \(z \in \mathbb{C}\) et \(\mathrm{Re}(z) > 0\), \[\hat{F}(z)=\int_0^X e^{-zt} F(t)\, dt + \frac{e^{-zX}}{z}\, L\, .\]
Si L≠0, alors z=0 est le pôle de \(\,\hat{F}\,\) avec la partie réelle la plus grande, et L est le résidu en z=0. Ainsi z=0 est aussi le pôle de \(\,(I-\hat{G}(z))^{-1} \hat{F}(z)\) avec la partie réelle la plus grande et \(R=(I-\hat{G}(0))^{-1} L\,\) est le résidu en z=0. La formule des résidus appliquée à (9) donne \[\Phi(t) \mathop{\longrightarrow}_{t \to \infty} R.\] Ceci reste vrai si L=0, car alors tous les pôles de \(\,(I-\hat{G}(z))^{-1} \hat{F}(z)\,\) sont dans le demi-plan gauche du plan complexe. \(\Phi(t)\) converge donc vers 0 si \(t \to \infty\). Dans tous les cas, il résulte de (6) \begin{equation}\tag{10} P(x,t) \mathop{\longrightarrow}_{t \to \infty} S(0,x) R + \int_0^x S(u,x) M(u)\, du, \quad \forall \, x\geq 0. \end{equation} C'est le troisième résultat.
Les exemples dans cette section sont conçus pour représenter des populations humaines: \(M_k(x)\) est l'immigration et \(d_k(x)\,\) la mortalité. S'il y a de l'émigration, seul change \(\,d_k(x)\).
La population est divisée entre hommes (k=1) et femmes (k=2). On suppose \[\Delta= \left (\begin{array}{ll} d_1 & 0\\ 0 & d_2 \end{array} \right ),\quad B= \left (\begin{array}{ll} 0 & B_{1,2}\\ 0 & B_{2,2} \end{array} \right ),\quad M= \left (\begin{array}{l} M_1 \\ M_2 \end{array} \right ),\] ce qui signifie que le nombre de naissances dépend du nombre de femmes mais pas du nombre d'hommes. Pour simplifier les formules, supposons que \(\,B_{1,2}(x)=B_{2,2}(x)=b(x)\). Cette hypothèse signifie que les probabilités pour un nouveau-né d'être un garçon ou une fille sont égales (en pratique, c'est presque vrai).
Parce que B est une matrice triangulaire supérieure, \(\,\hat{G}(0)\,\) a la même structure. Donc le rayon spectral est \[\rho(\hat{G}(0))=\int_0^\infty b(x)\, e^{-\int_0^x d_2(u)\, du}\, dx.\] On suppose \(\rho(\hat{G}(0)) < 1\). Le vecteur R se calcule facilement: \[R_1=R_2=\frac{\int_0^\infty b(x) \int_0^x e^{-\int_u^x d_2(v)\, dv} M_2(u)\, du\, dx}{1-\int_0^\infty b(x)\, e^{-\int_0^x d_2(u)\, du} dx}\, .\] On a alors \(\, \forall x\geq 0\), \begin{align*} &P_1(x,t) \mathop{\longrightarrow}_{t \to \infty} e^{-\int_0^x d_1(u)\, du} R_1 + \int_0^x e^{-\int_u^x d_1(v)\, dv} M_1(u)\, du,\\ &P_2(x,t) \mathop{\longrightarrow}_{t \to \infty} e^{-\int_0^x d_2(u)\, du} R_2 + \int_0^x e^{-\int_u^x d_2(v)\, dv} M_2(u)\, du. \end{align*}
La population est divisée entre les hommes nés dans le pays (k=1), les femmes nées dans le pays (k=2) et les immigrés de première génération, hommes (k=3) ou femmes (k=4). On suppose \[\Delta= \left (\begin{array}{llll} d_1 & 0 & 0 & 0\\ 0 & d_2 & 0 & 0\\ 0 & 0 & d_3 & 0\\ 0 & 0 & 0 & d_4 \end{array} \right ),\quad B= \left (\begin{array}{llll} 0 & B_{1,2} & 0 & B_{1,4}\\ 0 & B_{2,2} & 0 & B_{2,4}\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 \end{array} \right ),\quad M= \left (\begin{array}{l} 0\\ 0\\ M_1 \\ M_2 \end{array} \right ),\] ce qui signifie que les femmes immigrées donnent naissance à des enfants du pays, avec un taux différent de celui des femmes nées dans le pays. Supposons aussi que \(\,B_{1,2}=B_{2,2}=b_2\) et \(B_{1,4}=B_{2,4}=b_4\). Parce que B et \(\,\hat{G}(0)\) sont des matrices triangulaires supérieures, \[\rho(\hat{G}(0))=\int_0^\infty b_2(x)\, e^{-\int_0^x d_2(u)\, du}\, dx.\] \(\rho(\hat{G}(0))\) ne dépend pas de \(b_4\). Dans ce modèle, un taux de fertilité élevé pour les immigrés ne peut changer une situation sous-critique en une situation surcritique (\(\rho(\hat{G}(0)) > 1\)). On suppose \(\,\rho(\hat{G}(0)) < 1\). Le vecteur R se calcule encore facilement: \[R_1=R_2= \frac{\int_0^\infty b_4(x) \int_0^x e^{-\int_u^x d_4(v)\, dv} M_4(u)\, du\, dx}{1-\int_0^\infty b_2(x)\, e^{-\int_0^x d_2(u)\, du} dx}\, ,\quad R_3=R_4=0.\] On a alors \(\, \forall x\geq 0\), \begin{align*} &P_1(x,t) \mathop{\longrightarrow}_{t \to \infty} e^{-\int_0^x d_1(u)\, du} R_1 ,\\ &P_2(x,t) \mathop{\longrightarrow}_{t \to \infty} e^{-\int_0^x d_2(u)\, du} R_2 \\ &P_3(x,t) \mathop{\longrightarrow}_{t \to \infty} \int_0^x e^{-\int_u^x d_3(v)\, dv} M_3(u)\, du,\\ &P_4(x,t) \mathop{\longrightarrow}_{t \to \infty} \int_0^x e^{-\int_u^x d_4(v)\, dv} M_4(u)\, du. \end{align*} Notez que ce deuxième exemple redonne le premier exemple si \(d_1=d_3\), \(d_2=d_4\) et \(b_2=b_4\,\), c'est-à-dire si les immigrés de première génération suivent immédiatement les taux de fertilité et de mortalité locaux. En effet, \(\,P_1+P_3\) remplace \(P_1\) et \(P_2+P_4\) remplace \(P_2\).
La population est divisée en nationaux, hommes (k=1) ou femmes (k=2), et étrangers, hommes (k=3) ou femmes (k=4). On suppose \[\Delta= \left (\begin{array}{llll} d_1 & 0 & -\tau_{1,3} & 0\\ 0 & d_2 & 0 & \tau_{2,4}\\ 0 & 0 & d_3+\tau_{1,3} & 0\\ 0 & 0 & 0 & d_4+\tau_{2,4} \end{array} \right ),\quad B= \left (\begin{array}{llll} 0 & B_{1,2} & 0 & 0\\ 0 & B_{2,2} & 0 & 0\\ 0 & 0 & 0 & B_{3,4}\\ 0 & 0 & 0 & B_{4,4} \end{array} \right ),\quad M= \left (\begin{array}{l} 0\\ 0\\ M_3 \\ M_4 \end{array} \right ),\] ce qui signifie que les femmes étrangères donnent naissance à des enfants étrangers, mais les étrangers peuvent changer de nationalité (ils sont transférés de la sous-population 3 ou 4 vers les sous-populations 1 ou 2). Pour simplifier, on suppose \(\,d_1=d_3\) et \(d_2=d_4\) : la mortalité des étrangers est la même que celle des nationaux. On suppose aussi \(\,B_{1,2}=B_{2,2}=b_2\) et \(B_{3,4}=B_{4,4}=b_4\). On a alors \[S(0,x)=\left (\begin{array}{cccc} S_{1,1}(0,x) & 0 & S_{1,3}(0,x) & 0\\ 0 & S_{2,2}(0,x) & 0 &S_{2,4}(0,x)\\ 0 & 0 & S_{3,3}(0,x) & 0\\ 0 & 0 & 0 & S_{4,4}(0,x) \end{array} \right ) \] avec \[ S_{1,1}(y,x)=e^{-\int_y^x d_1(u)\, du},\quad S_{2,2}(y,x)=e^{-\int_y^x d_2(u)\, du},\] \[ S_{3,3}(y,x)=e^{-\int_y^x [d_1(u)+\tau_{1,3}(u)]\, du},\quad S_{4,4}(y,x)=e^{-\int_y^x [d_2(u)+\tau_{2,4}(u)]\, du}, \] et \begin{align*} S_{1,3}(y,x)&=e^{-\int_y^x d_1(u)\, du} + \int_y^x \tau_{1,3}(z) \, e^{-\int_z^x d_1(u)\, du -\int_y^z [d_1(u)+\tau_{1,3}(u)] du} dz,\\ S_{2,4}(y,x)&=e^{-\int_y^x d_2(u)\, du} + \int_y^x \tau_{2,4}(z) \, e^{-\int_z^x d_2(u)\, du -\int_y^z [d_2(u)+\tau_{2,4}(u)] du} dz. \end{align*} On a ainsi \[\hat{G}(0)=\left (\begin{array}{cccc} 0 & \int_0^\infty b_2(x) \, S_{2,2}(x)\, dx& 0& \int_0^\infty b_2(x)\, S_{2,4}(x)\, dx\\ 0 & \int_0^\infty b_2(x) \, S_{2,2}(x)\, dx& 0& \int_0^\infty b_2(x) \, S_{2,4}(x)\, dx\\ 0 & 0& 0& \int_0^\infty b_4(x)\, S_{4,4}(x)\, dx\\ 0 & 0& 0& \int_0^\infty b_4(x)\, S_{4,4}(x)\, dx \end{array} \right )\] \(\hat{G}(0)\) est une matrice triangulaire supérieure, \[\rho(\hat{G}(0))=\max \left \{ \int_0^\infty b_2(x)\, e^{-\int_0^x d_2(u)\, du}\ ;\ \int_0^\infty b_4(x)\, e^{-\int_0^x [d_2(u)+\tau_{2,4}(u)]\, du} \right \}. \] On suppose \(\rho(\hat{G}(0)) < 1\). Le vecteur R se calcule encore aisément. On définit \begin{align*} L_2&=\int_0^\infty b_2(x) \int_0^x S_{2,4}(y,x) M_4(y)\, dy \, dx\\ L_4&=\int_0^\infty b_4(x) \int_0^x S_{4,4}(y,x) M_4(y)\, dy \, dx. \end{align*} On a \(L=(L_2,\, L_2,\, L_4,\, L_4)\) et \begin{align*} &R_1=R_2=\frac{L_2+\hat{G}_{2,4}(0)L_4/(1-\hat{G}_{4,4}(0))}{1-\hat{G}_{2,2}(0)},\quad R_3=R_4=\frac{L_4}{1-\hat{G}_{4,4}(0)}\, . \end{align*} Enfin, on a \(\, \forall x\geq 0\), \begin{align*} P_1(x,t) \mathop{\longrightarrow}_{t \to \infty} &S_{1,1}(0,x)R_1+S_{1,3}(0,x) R_3+\int_0^x S_{1,3}(u,x)\, M_3(u)\, du\\ P_2(x,t) \mathop{\longrightarrow}_{t \to \infty} &S_{2,2}(0,x)R_2+S_{2,4}(0,x) R_4+\int_0^x S_{2,4}(u,x)\, M_4(u)\, du\\ P_3(x,t) \mathop{\longrightarrow}_{t \to \infty} &S_{3,3}(0,x)R_3+\int_0^x S_{3,3}(u,x)\, M_3(u)\, du\\ P_4(x,t) \mathop{\longrightarrow}_{t \to \infty} &S_{4,4}(0,x)R_4+\int_0^x S_{4,4}(u,x)\, M_4(u)\, du. \end{align*} Notons que ce troisième exemple se réduit au premier exemple si \(\tau_{1,3}=\tau_{1,2}=0\,\), c'est-à-dire si les sous-populations {1,2} et {3,4} ne se mélangent pas.
Pour illustrer cette étude, on a écrit un programme qui tourne dans l'environnement Scilab, un logiciel libre de calcul numérique disponible à l'adresse www-rocq.inria.fr/scilab. Le programme, nommé census.sci, se trouve avec les fichiers qui contiennent les données pour la France à l'adresse www.ann.jussieu.fr/~bacaer/Prog/Immigration/immigration/immigration.html. Il résout le système d'équations aux dérivées partielles en utilisant la méthode des différences finies. On choisit \(\,\delta t > 0\) et \(\delta x > 0\). \(P_k^{i,j}\,\) est la valeur de \(\,P_k(x,t)\) si \(x=i\, \delta x\) et \(t=j\, \delta t\). On utilise des notations similaires pour \(\,\Delta_{k,l}\), \(M_k\), \(B_{k,l}\) et \(P_k^0\). On a alors \[P_k^{i,0}=(P_k^0)^i,\quad \forall i\geq 0,\] \[P_k^{0,j+1}=\sum_{l=1}^K \sum_{i=0}^\infty B_{k,l}^i P_l^{i,j},\quad \forall j\geq 0,\] \[\frac{P_{k}^{i,j+1}-P_k^{i,j}}{\delta t} + \frac{P_k^{i,j}-P_k^{i-1,j}}{\delta x} + \sum_{l=1}^K \Delta_{k,l}^i P_l^{i,j} = M_k^i,\quad \forall i\geq 1,\quad \forall j\geq 1.\] Notez les discrétisations, progressive par rapport au temps et rétrograde par rapport à l'âge. Les équations sont en fait des équations d'advection, donc on doit tenir compte de la direction des courbes caractéristiques pour avoir un schéma qui converge. La condition \(\,\delta t\leq \delta x\,\) doit aussi être respectée. Dans le programme, on a toujours pris \(\,\delta x\,\) égal à une année.
La syntaxe est la suivante:
\(\text{census(X,K,annees,gauche,droit,pfichiers,bindices,dindices,dfichiers,mindices,mfichiers)}\).Définitions:
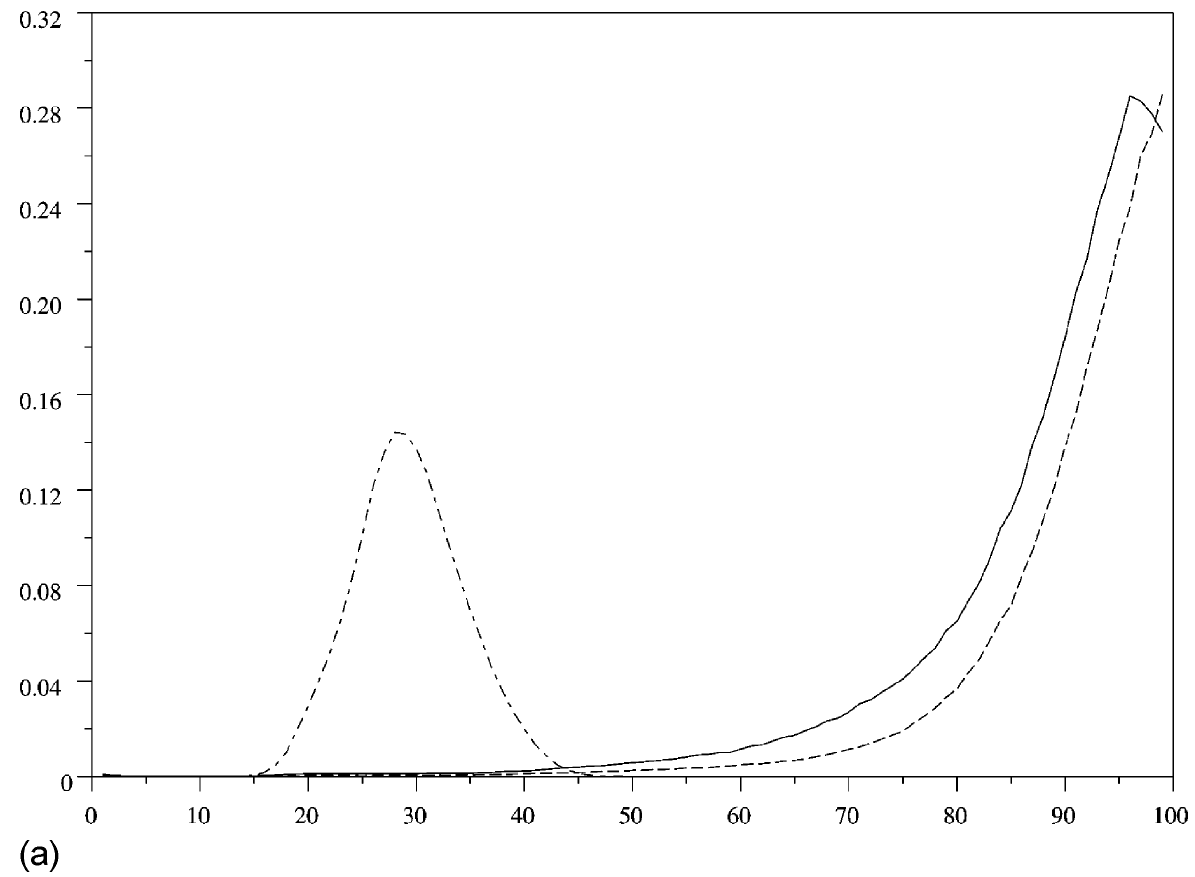
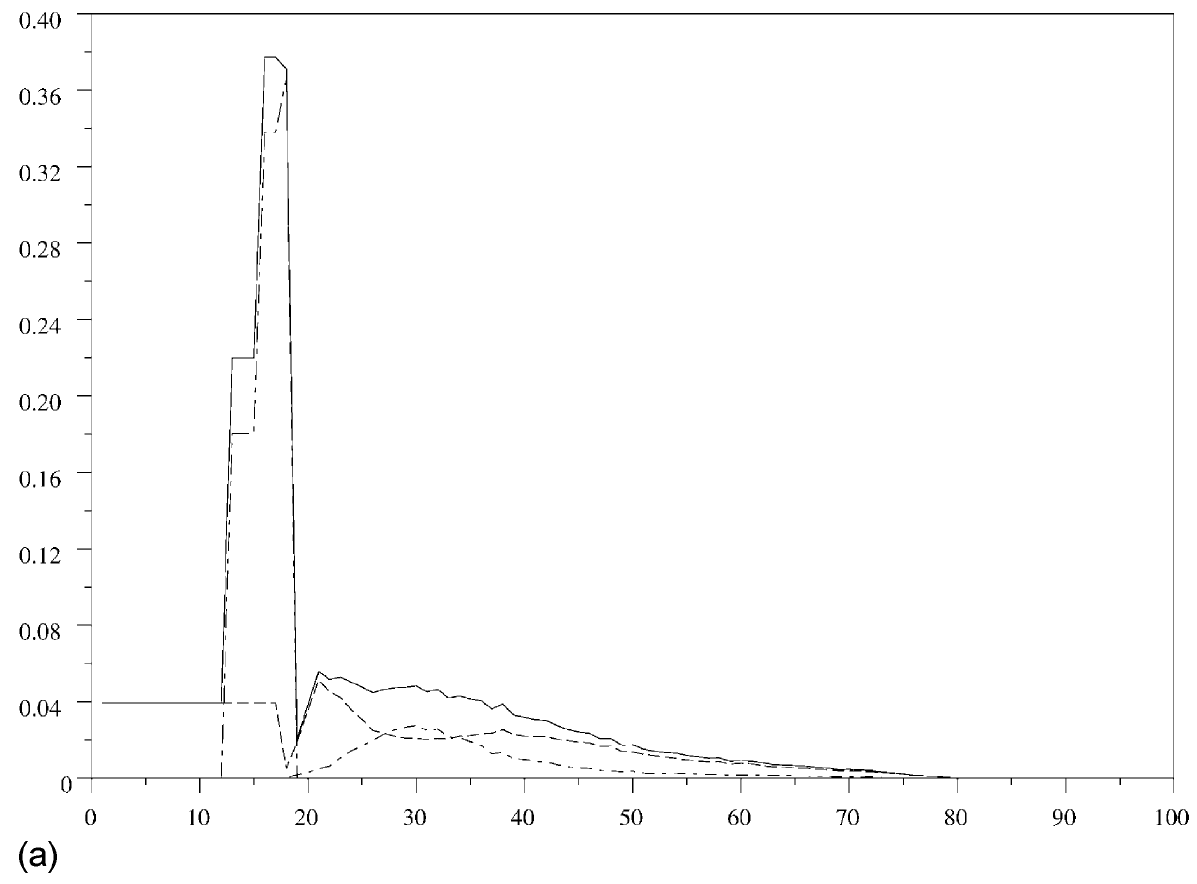
Comme données initiales pour les populations masculines et féminines, on prend les résultats du recensement de 1999 en France. Les taux de fertilité et de mortalité sont calculés avec les données de la même année (Beaumel, Doisneau et Vatan, 2001): voir la figure 1(a). Si l'immigration est nulle, alors
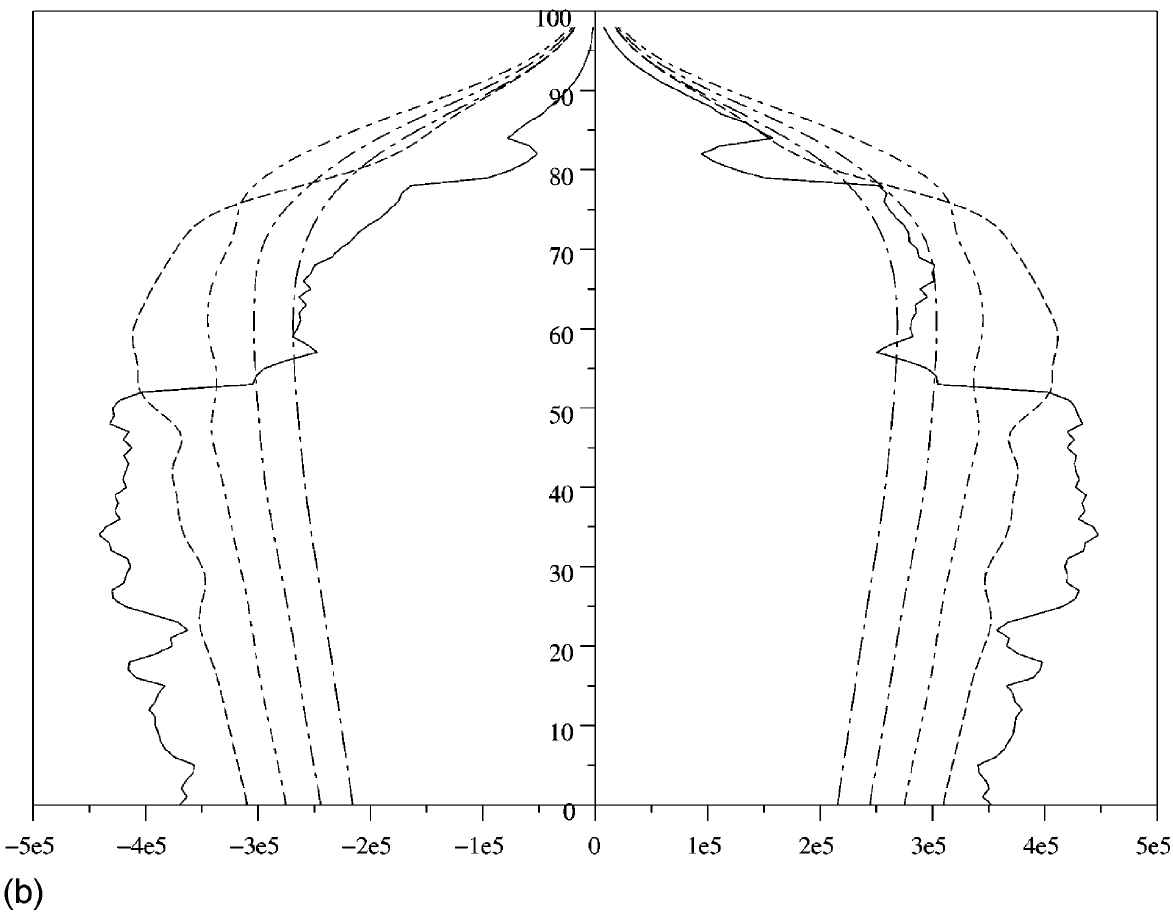
\(\text{census(99,2,[0 25 50 75 100],[1 0],[0 1],['male.dat' 'female.dat',[1 2;2 2],['malebirth.dat' 'femalebirth.dat'],}\) \(\text{[1 1; 2 2],['maledeath.dat', 'femaledeath.dat'],[],[])}\)donne la figure 1(b), où la population finit par converger vers 0, mais assez lentement.


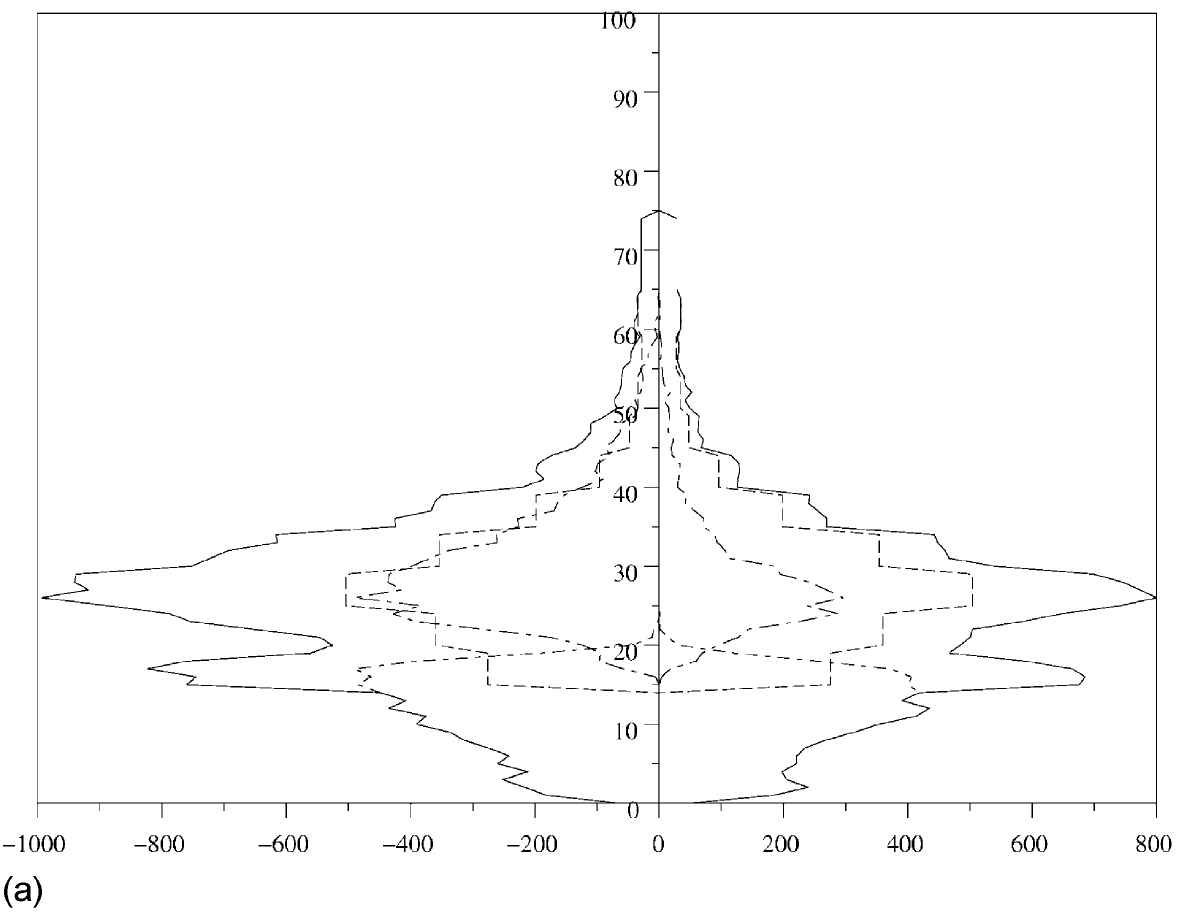
On inclut désormais l'immigration \(M(x)\). Dinh (1994) a calculé \(\,M(x)\,\) en utilisant les résultats de deux recensements consécutifs et les données sur les naissances et les morts entre ces deux recensements. La méthode a donné des résultats raisonnables jusqu'aux années 1980. Mais entre 1990 et 1999, l'immigration totale était du même ordre que les erreurs sur les recensements, de sorte que les calculs ne donnent pas de résultat raisonnable. Une autre méthode consiste à utiliser les données annuelles de l'Office des migrations internationales (1999), qui sont résumées dans la figure 2(a). L'immigration totale est la somme des travailleurs immigrés, des immigrés qui ont obtenu une carte de séjour, et des immigrés dans le cadre du regroupement familial. On a trouvé des données par âge pour les immigrés qui ont obtenu une carte de séjour (d'où la fonction en escalier dans la figure 2(a)), mais pas pour les adultes dans le cadre du regroupement familial. Pour les calculs, seules les courbes extérieures de la figure 2(a) sont utiles. Alors l'instruction
\(\text{census(99,2,[0 25 50 75 100],[1 0],[0 1],['male.dat' 'female.dat'],[1 2; 2 2],['malebirth.dat' 'femalebirth.dat'],}\) \(\text{[1 1; 2 2],['maledeath.dat' 'femaledeath.dat'],[1 2],['maleimmigrant.dat' 'femaleimmigrant.dat']);}\)produit la figure 2(b). La structure de la population converge lentement vers un état stationnaire avec une population totale petite (non représentée dans la figure).
Ce type de modèle (avec \(K=2\)) est semblable aux versions discrètes utilisées par l'INSEE (Brutel, 2001). Il est facile de critiquer ce modèle. D'un côté, on utilise des chiffres d'immigration assez faibles. D'un autre côté, on utilise les données actuelles pour calculer le taux de naissances. Actuellement, ce taux est assez élevé. C'est dû en partie au pourcentage élevé d'immigrés dans la population et au fait que les immigrés ont des taux de fertilité plus élevés que les Français. Ceci nous conduit aux deux modèles suivants.
Comme données initiales pour les populations masculines et féminines nées en France ou immigrées, on prend les résultats du recensement de 1999 (INSEE, 2001). On utilise le même profil d'immigration que dans le premier exemple. Pour estimer les taux de fertlité, on suppose qu'il existe un nombre \(\,\varepsilon > 0\) avec \(B_{1,4}(x)=(1+\varepsilon)B_{1,2}(x)\) et \(B_{2,4}(x)=(1+\varepsilon)B_{2,2}(x)\,\) pour tout x. On connaît le nombre total d'enfants nés de mère étrangère (qui forment plus ou moins un sous-ensemble des femmes immigrées) et aussi le nombre de femmes étrangères. On obtient \(\,\varepsilon=\mbox{0,6}\). Alors
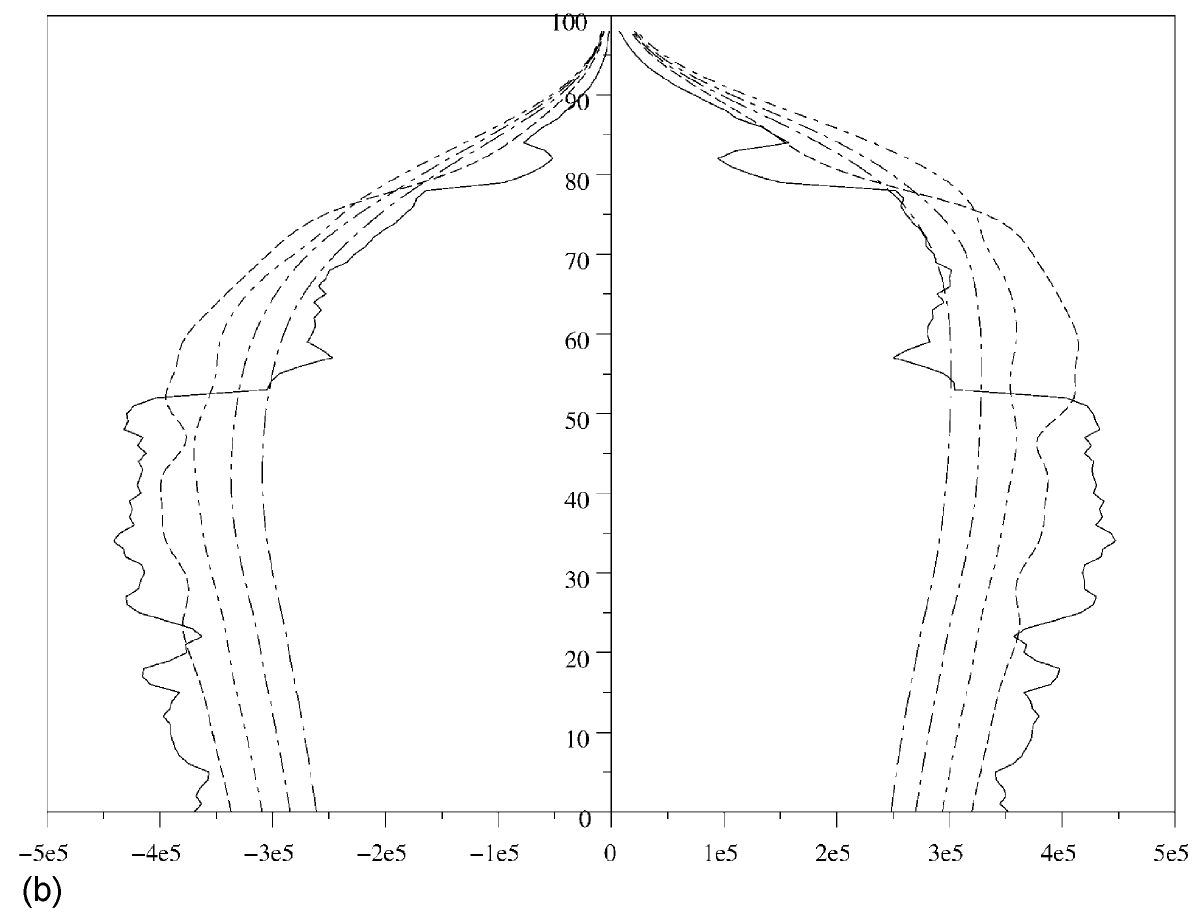
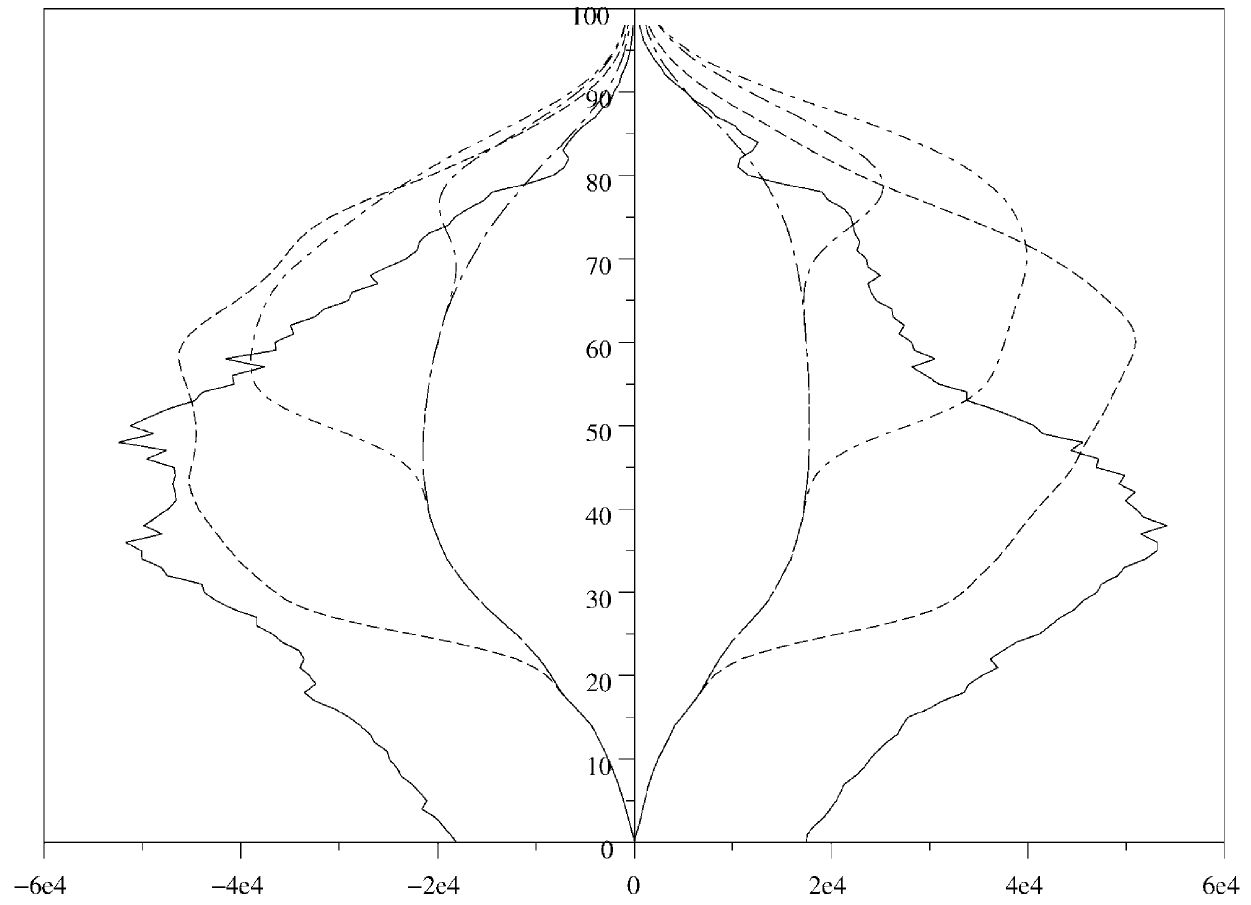
\(\text{census(99,4,[0 25 50 75 100],[0 0 1 0],[0 0 0 1],['malenative.dat' 'femalenative.dat' 'maleimmigrate.dat' 'femaleimmigrate.dat'],}\) \(\text{[1 2; 2 2; 1 4; 2 4],['malenativemother.dat' 'femalenativemother' 'maleimmigratemother.dat' 'femaleimmigratemother.dat'],}\) \(\text{[1 1; 2 2; 3 3; 4 4],['maledeath.dat' 'femaledeath.dat' 'maledeath.dat' 'femaledeath.dat'],}\) \(\text{[3 4],['maleimmigrant.dat' 'femaleimmigrant.dat']);}\)produit la figure 3 pour la pyramides des âges des immigrés. La pyramide converge rapidement (après 100 ans) vers un état stationnaire.
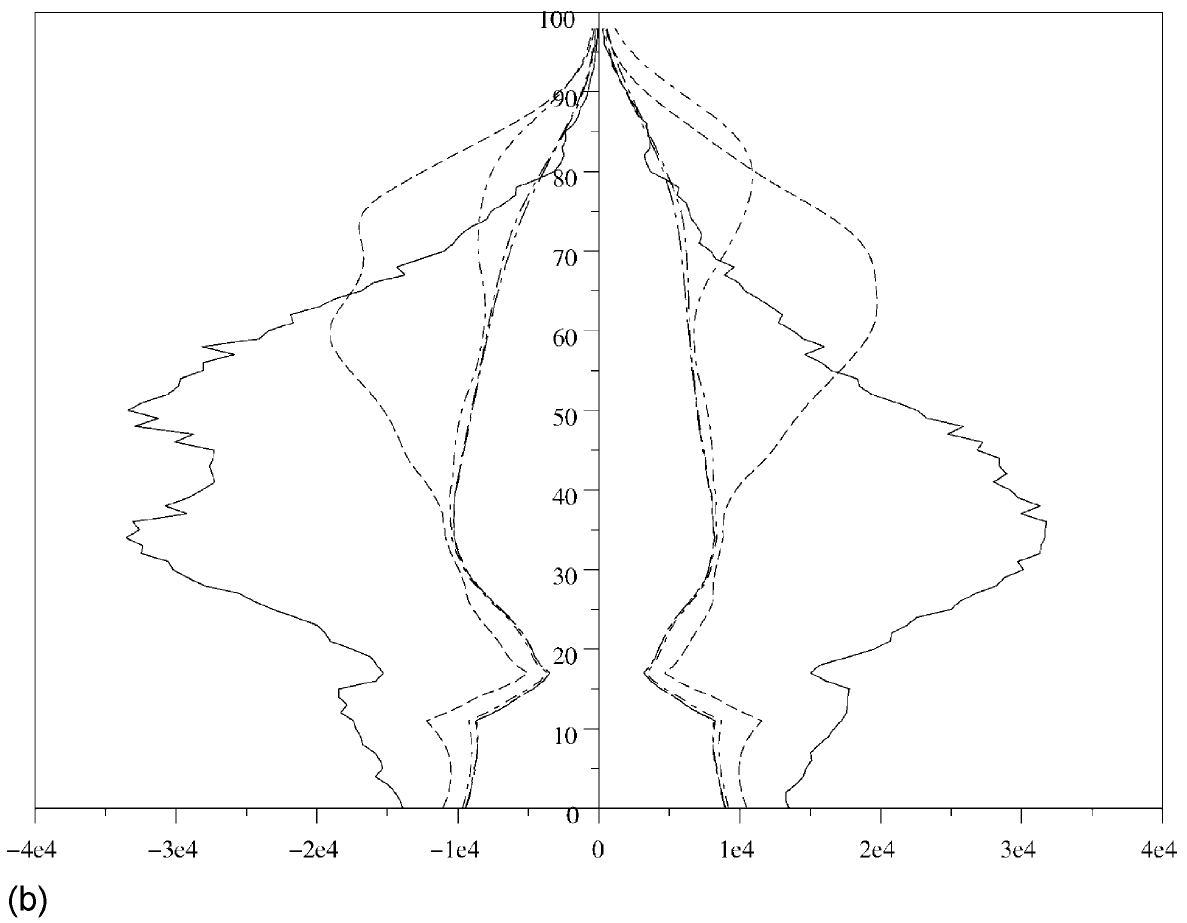
Comme donnée initiale pour la population masculine et féminine de nationalité française et celle étrangère, on prend les résultats du recensement de 1999 (INSEE, 2001). On utilise le même profil d'immigration que dans le premier exemple. Pour estimer les taux de fertlité, on suppose encore qu'il existe un nombre \(\,\varepsilon > 0\) avec \(B_{3,4}(x)=(1+\varepsilon)B_{1,2}(x)\) et \(B_{4,4}(x)=(1+\varepsilon)B_{2,2}(x)\,\) pour tout x. Connaissant le nombre total d'enfants nés de mère étrangère, on obtient \(\varepsilon=\mbox{0,56}\). Pour les taux de changement de nationalité, on suppose que \(\,\tau_{1,3}(x)=\tau_{2,4}(x)=\tau(x)\). Avec les données du Ministère de la justice (2001), on a une estimation de \(\,\tau(x)\). Voir figure 4(a). Cette estimation fait la somme des contributions de trois types de procédure, également représentées dans la figure 4(a): sans formalité ou par anticipation (enfants étrangers nés en France qui deviennent citoyens à 18 ans), par décret (étrangers ayant vécu longtemps en France et leurs enfants) et par déclaration (mariage avec un citoyen français). Dans tous les cas où la structure par âge n'est donnée que par groupe d'âges, on a utilisé des fonctions en escalier comme approximation. Alors l'instruction
\(\text{census(99,4,[0 25 50 75 100],[0 0 1 0],[0 0 0 1],['malefrench.dat' 'femalefrench.dat' 'maleforeign.dat' 'femaleforeign.dat'],}\) \(\text{[1 2; 2 2; 3 4; 4 4],['malefrenchmother.dat' 'femalefrenchmother.dat' 'maleforeignmother.dat' 'femaleforeignmother.dat'],}\) \(\text{[1 1; 1 3; 2 2; 2 4; 3 3; 4 4],['d11.dat' 'd13.dat' 'd22.dat' 'd24.dat' 'd33.dat' 'd44.dat'],[3 4],}\) \(\text{['maleimmigrant.dat' 'femaleimmigrant.dat']);}\)produit la figure 4(b) pour la pyramides des âges des étrangers. La pyramide converge après 100 ans vers un état stationnaire.
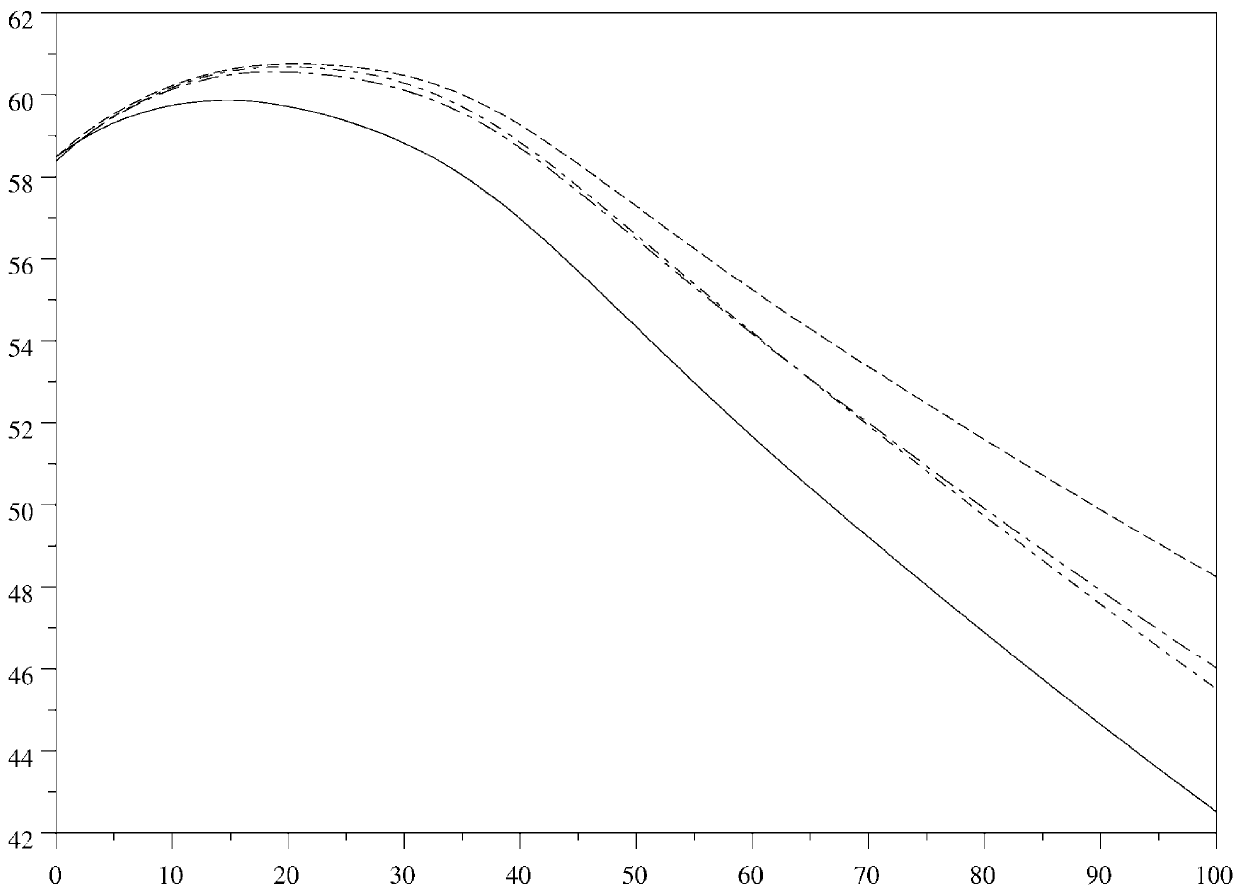
Pour comparer les différents modèles, la figure 5 montre les projections pour la population totale. La courbe la plus basse est celle sans immigration. La courbe la plus haute est celle avec immigration mais sans différence de fertilité (premier exemple). Les deux courbes très proches intermédiaires correspondent au deuxième et au troisième exemple, où les personnes nées en France (resp. les citoyens français) sont distinguées des immigrés (resp. des étrangers). La différence pour la population totale entre ces deux derniers modèles et le premier exemple avec immigration est d'environ 0,7 million après 50 ans et d'environ 2,5 millions après 100 ans.
Arino et Smith (1998) ont étudié un modèle plus complexe avec une variable de plus, qui se généralise de la manière suivante. Chacune des K sous-populations est divisée en deux:
Bien que le modèle suive correctement les processus d'évolution, il est difficile à mettre en œuvre car des données ne sont pas connues, comme par exemple \(R_k^0(x,y)\) pour 1≤k≤4. Ces données seraient peut-être accessibles à travers le méga-fichier du recensement de 1999, mais elles n'ont pas été publiées.
Une manière de contourner ce problème est de supposer que \(\Delta^R\), \(B^R\) et \(\tau^R\,\) ne dépendent pas de y. Mais cela réduit plus ou moins le modèle complexe à celui de la section 3.3. En effet, on définit \[S(x,t)=\int_0^x R(x,y,t)\, dy\quad ,\quad P(x,t)=\left (\begin{array}{c} Q(x,t) \\ S(x,t) \end{array} \right ).\] \(P(x,t)\) est l'unique solution du système (1)-(2)-(3) avec \[\Delta = \left (\begin{array}{c|c} \Delta^Q & 0 \\ \hline -\tau^Q & \Delta^R-\tau^R \end{array} \right ),\quad B=\left (\begin{array}{c|c} B^Q & B^R \\ \hline 0 & 0 \end{array} \right ),\quad M=\left (\begin{array}{c} 0 \\ m \end{array} \right ).\] Pour ce dernier modèle, les données sont disponibles pour faire les calculs. Le résultat ne serait pas très différent de celui de la figure 4.
Le modèle linéaire (1)-(2)-(3) pourrait être utile pour d'autres problèmes, par exemple pour les populations de poissons. Les sous-populations peuvent ne pas résider au même endroit. On peut imaginer des sous-populations en différents sites, avec des migrations comme dans Arino et Smith (1998). La fonction \(\,d_k(x)\,\) peuvent inclure la pêche. \(M_k(x)\) pourrait représenter la réintroduction des poissons d'une espèce menacée, comme le saumon en France.
On peut aussi élaborer des versions non linéaires ou non homogènes du modèle, comme chez Hoppensteadt (1975), Webb (1985) ou Cushing (1998).