Récolte de bois de feu au Niger et une généralisation de la formule de Faustmann

Résumé

Dans certaines forêts du Niger, où ont été établis des « marchés ruraux contrôlés », le bois de feu est récolté suivant une politique du type suivant : toutes les T années, couper les arbres morts et les arbres vivants d'un diamètre supérieur à D. Les arbres morts constituent en général la majeure partie de la récolte. Dans cet article, on présente un modèle simple en temps continu pour la gestion de ces parcelles forestières inéquiennes sujettes à un taux de mortalité α élevé, et l'on obtient une formule pour le cycle et le diamètre de coupe qui optimisent le revenu actualisé, avec un horizon infini. La formule classique de Faustmann pour les parcelles équiennes correspond à la limite \(\,\alpha\to 0\) et \(D= 0\) (coupe claire).

1.   Introduction

    Au Niger, le bois est toujours la source d'énergie la plus importante pour cuire la nourriture. À cause de la sécheresse, d'une population urbaine croissante et d'un accès en partie incontrôlé à la ressource, la pression sur les forêts autour de villes telles que Niamey est élevée. Depuis 1989, une nouvelle stratégie gouvernementale a conduit à la protection de certaines zones forestières, où la récolte est gérée de manière durable. La récolte est vendue exclusivement dans des marchés proches avec autorisation administrative. Un système différentiel de taxes encourage les négociants à acheter le bois de feu de ces structures plutôt que d'organiser la récolte incontrôlée des forêts [1].

    Deux systèmes de gestion ont été choisis. Dans les « marchés ruraux orientés », seuls les arbres morts sont récoltés. Dans les « marchés ruraux contrôlés », on coupe aussi certains arbres vivants et la coupe est organisée en cycle pour permettre une rotation spatiale. On fixe parfois une limite inférieure pour le diamètre des arbres vivants à couper. Cela peut prendre plusieurs cycles pour qu'un arbre atteigne ce diamètre, de sorte que les arbres morts forment en géneral la majorité de chaque récolte. La longueur du cycle est typiquement fixée entre 5 et 10 ans.

    La politique de récolte dans ces marchés ruraux contrôlés est donc assez semblable à la coupe sélective pratiquée sur des parcelles inéquiennes dans d'autres parties du monde. Mais l'importance des arbres morts est moins habituelle à cause de sa destination (le bois mort est meilleur que le bois vert pour la cuisson des aliments), l'absence de transformation et sa disponibilité (le climat sahélien provoque une forte mortalité des arbres).

    Malgré une littérature abondante qui traite d'extensions diverses de la formule classique de Faustmann [2,3] pour le problème de la rotation optimale ([4] et les 300 articles recensés dans [5]), aucune formule simple n'a été proposée pour le cycle optimal de coupe et le diamètre optimal de parcelles inéquiennes sujettes à une mortalité élevée, où les arbres morts forment la plus grande part de la récolte pour servir de bois de feu. Dans [6], une formule explicite est obtenue mais pour des forêts équiennes sujettes à une faible mortalité catastrophique telle que l'incendie. Le modèle utilisait une variable de temps continue, et la formule était obtenue en utilisant la théorie des processus de renouvellement avec récompense. Il faut insister sur ce qu'avec une forte mortalité naturelle, des arbres isolés meurent de temps en temps et il peut y avoir un délai avant qu'ils ne soient coupés lors de la récolte planifiée suivante. Au contraire, avec une mortalité catastrophique due aux incendies, la forêt entière est touchée presque instantanément et les arbres sont retirés peu de temps après. Dans le premier cas, une rotation spatiale simple peut être maintenue, tandis que c'est impossible dans le deuxième cas, comme le signale [6].

    On trouve dans [7] une formule qui généralise celle de Faustmann pour les parcelles inéquiennes, mais le modèle se concentrait sur la partie économique sans tenir compte d'un modèle de croissance biologique particulier. Cette formule a été utilisée dans [8] en combinaison avec un modèle matriciel en temps discret semblable à [9,10] pour la croissance; mais aucune formule simple pour le cycle optimal de coupe n'a été trouvée, de sorte que les résultats ne reposaient que sur des simulations. Plusieurs articles, tels que [11,12], insiste sur le fait que le modèle de Faustmann et nombre de ses généralisations sont des exemples particuliers de processus de décision markoviens, pour lesquels on peut utiliser des techniques de programmation dynamique. On se focalise alors plus sur les algorithmes numériques que sur des formules explicites. Dans toutes ces références, peu d'attention est accordée à la mortalité naturelle car dans un contexte européen ou nord-américain, elle est relativement négligeable comparée à plusieurs autres facteurs.

    L'objectif de cet article est donc de trouver, dans le cadre d'un modèle simple de parcelle inéquienne sujette à une mortalité élevée, une formule explicite pour le durée du cycle optimal et le diamètre de coupe optimal. Le critère d'optimisation est le même que dans le modèle de Fautmann, à savoir le revenu actualisé sur un horizon infini. L'intérêt est surtout théorique puisque à l'évidence, en dépit de [13], beaucoup de travail de terrain est encore nécessaire avant d'obtenir suffisamment de données pour calibrer le modèle aux forêts du Niger. Cependant, à mesure que de plus en plus de marchés ruraux contrôlés sont organisés au Niger et dans toute la zone sahélienne, plus de données seront disponibles et l'intérêt pourrait passer de comment gérer la forêt à comment optimiser la gestion. Le modèle peut aussi servir de base pour le développement de modèles plus complexes et plus réalistes, pour prendre en compte par exemple les fluctuations de prix rapportées dans [14].

    L'article est organisé de la façon suivante. Dans la section 2, on introduit les notations du modèle. Dans la section 3, on obtient une formule pour le cycle de coupe optimal et le diamètre optimal, puis on en discute en utilisant une expression mathématique simple pour la courbe de croissance des arbres. Dans la section 4, on montre que la formule classique de Faustmann correspond à la limite d'une mortalité négligeable (\(\alpha\to 0\)) et d'un diamètre de coupe \(D=0\,\) (coupe claire). On montre aussi que la formule pour le rendement moyen de parcelles équiennes sujettes à une mortalité faible mais catastrophique telle que les incendies, donnée dans [6], correspond à la limite d'un cycle de coupe \(T\to 0\) avec un taux d'actualisation \(\beta\to 0\). On présente aussi d'autres extensions de la formule: à une mortalité qui dépend de l'âge et à une possible différence de prix entre le bois mort et le bois vert récemment coupé. Elles peuvent servir dans d'autres contextes.

2.   Un modèle simple

    On suppose :

• une parcelle a un nombre fixé N d'emplacements pour que des arbres poussent. N est un grand nombre.
• \(V(x)\,\) est le volume d'un arbre d'âge x, \(V(0)=0\)
• le prix P par unité de volume de bois est constant
• \(c\) est le coût de préparation pour la croissance d'un nouvel arbre
• \(c'\) est un coût fixe par récolte
• α est la mortalité des arbres : pendant un petit intervalle de temps dt, \(\,\alpha\, dt\,\) est le pourcentage d'arbres qui meurent (si l'on pense au modèle comme étant déterministe), ou la probabilité qu'un arbre meure (si l'on pense au modèle comme étant stochastique). Pour le moment, on suppose que α est indépendant de l'âge, mais cette hypothèse sera abandonnée dans la section 4.
• la durée du cycle de coupe est T
• toutes les T années, la récolte consiste en tous les arbres morts et tous les arbres vivants dont le diamètre est supérieur à D
• X est l'âge auquel les arbres atteignent le diamètre D.

    On suppose que la régéneration est purement artificielle: les arbres qui ont été coupés sont remplacés sans délai par de nouveaux arbres d'âge 0, de sorte que le nombre total d'arbres reste constant. On suppose que la régénération naturelle est négligeable pendant une rotation. Enfin, soit β un facteur d'actualisation tel que le revenu au temps t=n T soit pondéré par un facteur \(\,e^{-\beta n T}\,\) dans le critère d'optimisation. Le problème est de choisir T et X pour optimiser l'espérance du revenu actualisé sur toutes les récoltes futures.

    Formellement,

• \(p(x,t)\,\) est l'espérance de la densité de population des arbres vivants d'âge x au temps t,
• \(q(x,t)\,\) est l'espérance de la densité de population des arbres morts d'âge x au temps t (lorsqu'ils meurent, les arbres arrêtent de vieillir),
• \(K_n\) est l'espérance du revenu de la récolte au temps \(t=n T\).

3.   Cycle de coupe et diamètre optimaux

    Indépendamment de la structure par âge de la condition initiale, les densités \(p(x,t)\) et \(q(x,t)\) convergent si \(t\to +\infty\) vers des solutions périodiques \(\widehat{p}(x,t)\) et \(\widehat{q}(x,t)\), avec \begin{align*} &\widehat{p}(x,nT^-)=N\, \frac{1-e^{-\alpha T}}{1-e^{-i\alpha T}} \sum_{k=1}^i e^{-k\alpha T}\, \delta_{x=kT}\\ &\widehat{q}(x,nT^-)=N\, \frac{1-e^{-\alpha T}}{1-e^{-i\alpha T}}\, \alpha\, e^{-\alpha x}\, 1_{x\in (0,iT)}\\ &\widehat{p}(x,nT^+)=N\, \frac{1-e^{-\alpha T}}{1-e^{-i\alpha T}} \sum_{k=0}^{i-1} e^{-k\alpha T}\, \delta_{x=kT} \end{align*} et \(\widehat{q}(x,nT^+)=0\). \(\,i=[X/T]+1\) (et \([X/T]\) est la partie entière de \(X/T\)). Noter que si \(X < T\) (de sorte que \(i=1\)), tous les arbres vivants qui atteignent \(t=nT^-\) ont le même âge (parcelle équienne) et sont récoltés à t=nT en même temps que les arbres morts (coupe claire). Au contraire, si \(\,X > T\) (de sorte que \(i\geq 2\)), les arbres vivants qui atteignent \(t=nT^-\) ont pour âge T, 2T, …, iT, (parcelle inéquienne) et seuls ceux âgés de iT sont récoltés à t=nT avec les arbres morts (sélection). Ainsi, le nombre entier \(\,i\,\) représente le nombre de cycles qu'un arbre peut continuer à croître avant d'être récolté, à moins de mourir, dans quel cas l'arbre est récolté pendant la première récolte suivant sa mort. Les arbres morts récoltés à t=nT donnent le revenu \[N\, \frac{1-e^{-\alpha T}}{1-e^{-i\alpha T}} \int_0^{iT} \alpha\, e^{-\alpha x}\, [P\, V(x)-c]\, dx\, .\] Les arbres vivants récoltés à t=nT sont ceux d'âge iT. Ils donnent le revenu \[N\, \frac{1-e^{-\alpha T}}{1-e^{-i\alpha T}}\, e^{-i\, \alpha\, T}\, [P\, V(iT)-c]\, .\] Le revenu total à t=nT est donc (après intégration par parties) \[K_n=N\, \frac{1-e^{-\alpha T}}{1-e^{-i\alpha T}}\, \Bigl [ P \int_0^{iT} e^{-\alpha x}\, V'(x)\, dx -c\Bigr ]\, -c'.\] Enfin, l'espérance du revenu total sur toutes les récoltes futures est \begin{equation} \frac{1}{e^{\beta T}-1}\Bigl \{ N\, \frac{1-e^{-\alpha T}}{1-e^{-i\alpha T}}\, \Bigl [P \int_0^{iT} e^{-\alpha x}\, V'(x)\, dx -c\Bigr ] - c'\Bigr \}\, , \end{equation} pour lequel on doit trouver le maximum, par rapport à T et X. De manière équivalente, le maximum doit être trouvé par rapport à T et l'entier \(i=[X/T]+1\). C'est la généralisation de la formule classique de Faustmann pour la gestion considérée (comme on le verra dans la section suivante). Pour réduire le nombre de paramètres de la discussion, écrivons la formule \[N P V_\infty\, \frac{1}{e^{\beta T}-1}\Bigl \{ \frac{1-e^{-\alpha T}}{1-e^{-i\alpha T}}\, \Bigl [ \int_0^{iT} e^{-\alpha x}\, \frac{V'(x)}{V_\infty}\, dx -\frac{c}{P V_\infty}\Bigr ] - \frac{c'}{N P V_\infty}\Bigr \}\, .\] \(V_\infty\) est le volume maximum qu'un arbre peut atteindre durant sa vie. Noter que

• \(c/(P V_\infty)\) est le rapport entre le coût de couper et replanter un arbre d'une part, la valeur maximale d'un arbre d'autre part
• \(c'/(N P V_\infty)\) est le rapport entre le coût fixe par récolte et la valeur maximale d'une parcelle.

    Pour discuter de cette formule, considérons une expression mathématique simple \(V(x)\) pour la courbe de croissance des arbres, ou de manière équivalente pour sa dérivée \(V'(x)\,\), par exemple \[V'(x)=V_\infty \, \frac{(\gamma/\tau)^{\gamma+1}}{\Gamma(\gamma+1)} \ x^\gamma\, e^{-\gamma\, x/\tau}\, ,\] où Γ est la fonction Gamma usuelle. Cette fonction, supposée représenter la vitesse de croissance, croît de 0 à un maximum qui est atteint en x=τ, puis décroît en convergeant vers 0 lorsque \(\,x\to \infty\). Donc \(V(x)=\int_0^x V'(\xi)\, d\xi\,\) est une fonction croissante qui est convexe pour x < τ et concave pour x > τ. La paramétrisation met en avant le volume maximum d'un arbre \(\,V_\infty=\lim_{x\to \infty} V(x)\).

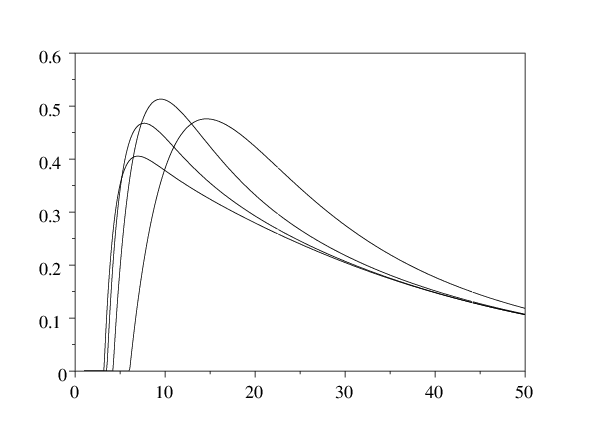
    La figure 1 illustre comment l'espérance du revenu actualisé peut varier en fonction de la longueur T du cycle de coupe pour différentes valeurs du diamètre de coupe, qui correspondent à i=1,…, 4. La courbe la plus à droite est celle avec \(\,i=1\,\) (coupe claire et parcelle équienne). La stratégie optimale est \(T^* \simeq \mbox{9,5}\) et \(i=2\), c'est-à-dire en coupant toutes les \(T^*\) années les arbres morts et les arbres vivants âgés de \(2\, T^*\) ou plus. Noter que toutes les courbes deviennent négatives quand T s'approche de 0 à cause du coût fixe non nul par récolte. Les valeurs des paramètres utilisées pour cette figure sont \(\, \alpha=\mbox{0,05}\) par année (l'espérance de vie des arbres est \(1/\alpha=20\) ans), \(\tau=10\) années (c'est l'âge auquel la croissance est la plus rapide) et \(\gamma=2\) pour la courbe de croissance, un facteur d'actualisation \(\beta=\mbox{0,03}\) par an, des coûts \(c/(P V_\infty)=0\) et \(c'/(N P V_\infty)=\mbox{0,1}\,\), et une valeur maximale de la parcelle normalisée \(NPV_\infty=1\).

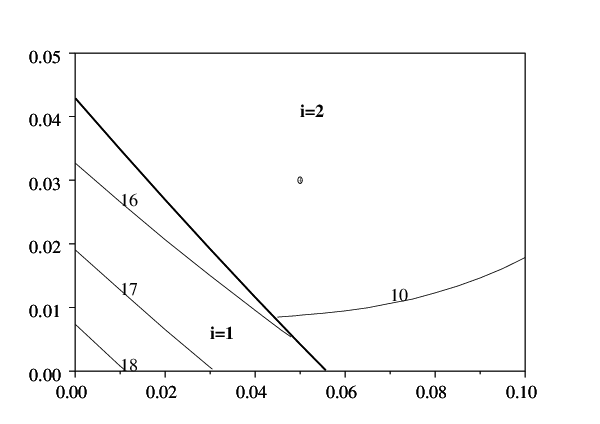
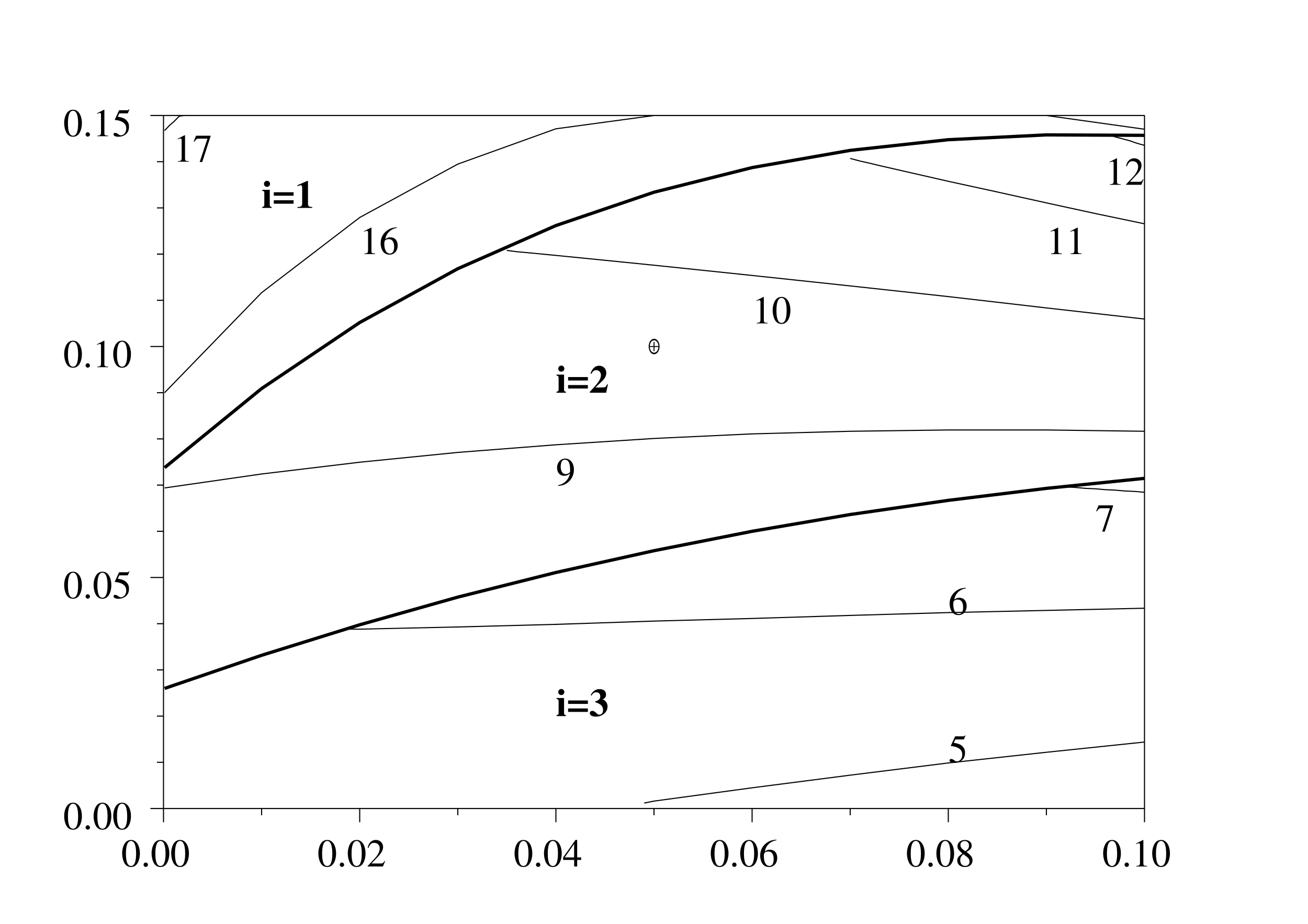
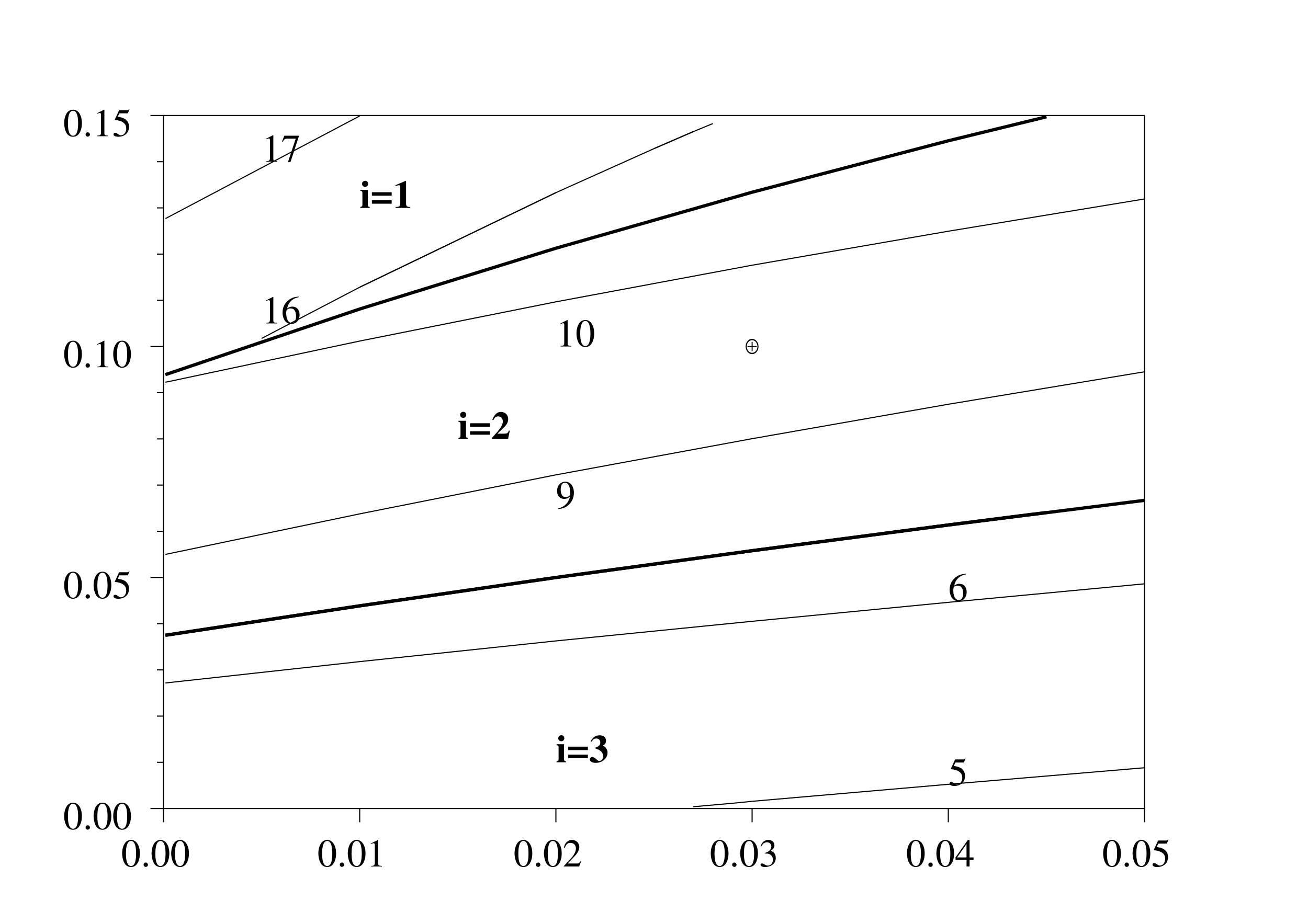
    La figure 2 illustre comment le cycle de coupe et le diamètre optimaux varient en fonction de la mortalité α , le taux d'actualisation β et le coût fixe par récolte. Les valeurs pour les paramètres fixes sont les mêmes que dans la figure 1. Comme attendu, des gestions inéquiennes avec un cycle de coupe court (représentées par les zones i=2 et i=3) sont plus profitables que des gestions équiennes (\(i=1\))

• lorsque la mortalité est élevée (figures en haut à gauche et en haut à droite),
• lorsque le facteur d'actualisation est élevé (figures en haut à gauche et en bas),
• ou lorsque le coût fixe par récolte est faible (en haut à droite et en bas).

    La figure 2 montre aussi les lignes de niveau de la longueur optimale du cycle de coupe. Noter qu'il n'y a pas de relation simple entre la longueur optimale du cycle de coupe et la mortalité: la première peut être une fonction croissante ou décroissante de la seconde, selon les valeurs des paramètres, comme dans la figure en haut à droite.

4.   Cas limites et extensions

    Si l'on fixe le diamètre critique D de coupe des arbres vivants à 0 (coupe claire), alors l'âge correspondant est X=0. Donc i=1 et la formule (1) se réduit à \[ \frac{1}{e^{\beta T}-1}\, \Bigl \{ N \Bigl [ P \int_0^{T} e^{-\alpha x}\, V'(x)\, dx -c \Bigr ] - c'\Bigr \}\, . \] Si de plus le coût fixe par récolte \(c'\) et la mortalité α sont négligeables, alors les formules se réduisent à celle de Faustmann [2,3] \[N\, \frac{P\, V(T)-c}{e^{\beta T}-1}\, .\]

    Un autre cas limite s'obtient si le facteur d'actualisation β et la longueur du cycle de coupe T convergent vers 0, ce qui correspond à regarder le revenu moyen avec une récolte continue des arbres morts et des arbres vivants dont l'âge est supérieur à X. Rappelons le lien entre le revenu moyen par an et le revenu actualisé sur toutes les récoltes futures: \[\lim_{\nu \to \infty} \frac{1}{\nu\, T} \sum_{n=1}^\nu K_n= \lim_{\beta\to 0} \beta \sum_{n=1}^\infty e^{-\beta n T}\, K_n\, .\] Gardons \(c'=0\). La formule (1) donne alors le revenu moyen \begin{equation} N\, \alpha \, \frac{P \int_0^X e^{-\alpha x}\, V'(x)\, dx -c}{1-e^{-\alpha X}}\, , \end{equation} et les densités \(p(x,t)\) et \(q(x,t)\) convergent vers les solutions stationnaires \[\widehat{p}(x)=N\, \frac{\alpha\, e^{-\alpha\, x}}{1-e^{-\alpha\, X}}\, 1_{x\in (0,X)}\] et \(\widehat{q}(x)=0\). La formule (2) est la même que celle dans [6] pour le revenu moyen dans les forêts sujettes à un risque d'incendie catastrophique. En effet, si \(\ T\to 0\), il n'y a pas de délai entre la mort de l'arbre et sa récolte, comme dans [6]. Il est donc normal que le revenu moyen soit le même. Cependant, la synchronisation des morts dans le cas de l'incendie conduit à une différence pour l'expression du revenu actualisé.

    Extensions. Supposons que la mortalité, au lieu d'être constante, dépende de l'âge. Définissons \[\Delta(x)=\exp(-\int_0^x \alpha(\xi)\, d\xi).\] Si Q est le prix du bois mort, si P est le prix du bois vert récemment coupé, l'espérance du revenu actualisé sur toutes les récoltes futures est alors \[\frac{1}{e^{\beta T}-1}\, \Bigl \{N\, \frac{\Delta(iT)\, [P\, V(iT)-c] - \int_0^{iT} \Delta'(x)\, [Q\, V(x)-c]\, dx}{\sum_{n=0}^{i-1} \Delta(nT)}-c' \Bigr \}\, ,\] avec \(\,i=[X/T]+1\). La formule (1) correspond à à Q=P et à α constant, de sorte que \(\Delta(x)=\exp(-\alpha\, x)\). Dans la limite où \(\beta\to 0\) et \(T\to 0\), cette formule (avec \(c'=0\)) conduit au revenu moyen \[N\, \frac{\Delta(X)\, [P\, V(X)-c]-\int_0^X \Delta'(x)\, [Q\, V(x)-c]\, dx}{\int_0^X \Delta(x)\, dx}\, ,\] une formule que l'on trouve dans [6] dans le contexte des forêts avec un risque d'incendie mais où une partie du bois brûlé peut être récupérée.

5.   Conclusion

    Dans le cadre d'un modèle simple, on a trouvé une formule pour la longueur du cycle de coupe et le diamètre optimaux lorsque la gestion consiste à couper toutes les T années les arbres morts et les arbres vivants avec un diamètre supérieur à D. Ce modèle a été conçu pour les forêts sujettes à une forte mortalité naturelle, où les arbres morts forment la part principale de la récolte et sont utilisés comme bois énergie. On a vu que la gestion inéquienne était plus favorable dans ces circonstances. Lorsque la mortalité naturelle est faible, le taux d'actualisation faible, ou le coût fixe par récolte élevé, la gestion équienne peut être plus profitable.

    La gestion des forêts au Niger et dans d'autres pays du Sahel est encore à ses débuts. La rotation n'a été introduite qu'il y a une décennie. Les données de terrain sont encore rares. Malgré les nombreuses recherches accumulées pendant plus de 150 ans sur le problème de la rotation optimale dans les pays développés, l'adaptation aux conditions locales est nécessaire. Dans cette étude, on ne se concentre que sur un seul aspect, à savoir la mortalité naturelle élevée. Éspérons que ce modèle microéconomique sera combiné avec des modèles macroéconomiques [17,18,19] pour fournir un outil de modélisation plus complet aux dédideurs publics.

Remerciements

    Le deuxième auteur remercie Édith Perrier (IRD), Alain Bertrand, Martine Antona, Christophe Le Page (CIRAD) et Aboubacar Ichaou (Ministère de l'environnement du Niger). Cet article est dédié à la mémoire d'Ovide Arino.

Références bibliographiques