Math. Biosci. Engin. 2 (2005) p. 227-238
Nicolas Bacaër
Institut de recherche pour le développement
32 avenue Henri Varagnat, 93143 Bondy Cedex, France
nicolas.bacaer@ird.fr
Laboratoire de Paludologie,
Institut de recherche pour le développement
B.P. 1386, Dakar, Sénégal
Cheikh.Sokhna@ird.sn
On développe un modèle mathématique représentant la diffusion de la résistance à un médicament antipaludique. La résistance ne peut se propager que si la reproductivité des parasites résistants est supérieure à la reproductivité des parasites sensibles, qui dépend de la fraction des personnes infectées qui sont traitées avec le médicament antipaludique. À la suite d'une étude linéarisée et de simulations numériques, on conjecture une expression pour la vitesse de propagation de la résistance. Elle dépend du rapport des deux reproductivités s, du coefficient de diffusion des moustiques, de la mortalité des moustiques infectés par les parasites résistants et du taux de guérison des personnes non immunisées infectées par les parasites résistants.
Le paludisme est une maladie parasitaire transmise à l'homme par la piqûre de moustiques. Il y a plusieurs centaines de millions de cas de paludisme chaque année, qui causent environ deux millions de décès. La mort peut être évitée par l'utilisation de médicaments antipaludiques, mais leur efficacité a beaucoup baissé au cours des dernières décennies. En effet, les parasites avec des gènes particuliers de résistance à un médicament survivent au traitement. À cause de de cet avantage sélectif et de la mobilité des hommes et des moustiques, les gènes peuvent se propager dans les populations sur de grandes zones. (Anderson et May, 1991, p. 608) montre ainsi une carte de la propagation de la résistance à la chloroquine, le médicament antipaludique le plus répandu, du début des années 1960 à la fin des années 1980 en Amérique du Sud, en Asie du Sud-Est et en Afrique. La montée de la résistance est responsable d'un accroissement considérable de la mortalité (Trape et coll., 1998). Dans certaines zones avec un pourcentage élevé de résistance à la chloroquine, des personnels de santé ont utilisé des médicaments de substitution tels que la sulphadoxine-pyriméthamine; mais de la résistance à ces nouveaux médicaments a également émergé (Bloland, 2001). Les dérivés de l'artémisinine, qui sont produits avec une plante chinoise traditionnelle, semblent actuellement être les seuls médicaments antipaludiques à être efficaces pour les prochaines années. Les autorités de santé publique doivent trouver de l'argent pour remplacer les médicaments inefficaces par des médicaments efficaces mais plus onéreux. Il faut aussi éviter ou au moins retarder l'apparition de nouvelles résistances.
D'un point de vue théorique, l'introduction de nouveaux médicaments antipaludiques peut être vue comme un problème de contrôle optimal d'un système dynamique complexe. Ce système inclut les hommes, les moustiques, les parasites sensibles et les parasites résistants. Il y a aussi les contraintes économiques comme les prix des médicaments et le budget pour la lutte contre le paludisme. Le contrôle peut être variable, par exemple le pourcentage de cas de paludisme traités avec le nouveau médicament. La modélisation de ces différents ingrédients peut aider les personnes qui conseillent les autorités de santé publique dans les pays où le paludisme est endémique. (Aneke, 2002 ; Koella et Antia, 2003) ont déjà développé des modèles épidémiologiques pour le paludisme résistant; (Laxminarayan, 2003) a étudié les contraintes économiques. Mais les modèles utilisés dans ces articles ne contenaient pas de dimension spatiale, ou seulement sous la forme de deux zones disjointes reliées par des migrations (Koella et Antia, 2003).
Cet article présente un modèle pour la propagation de la résistance dans des populations spatialement inhomogènes mais laisse les aspects économiques de côté. Le modèle commence avec quelques parasites résistants qui ont été introduits dans une zone par des hommes mais considère ensuite la zone comme fermée aux migrations; il se concentre sur la diffusion de la résistance due à la mobilité des moustiques, qui peuvent explorer quelques kilomètres carrés pendant leur vie. Puisque la plupart des piqûres se produisent la nuit, période d'activité des moustiques anophèles femelles qui sont le vecteur du paludisme, et puisque les personnes dorment en général au même endroit chaque nuit, on néglige la mobilité humaine en première approximation. Bien sûr, la propagation de la résistance fait intervenir plusieurs phénomènes. Certains se retrouvent dans le modèle. D'autres sont omis pour pouvoir analyser le modèle mathématiquement, par exemple la génétique de la reproduction sexuelle des parasites (Hastings, 2001) ou la variabilité génétique dans la population humaine (Feng et coll., 2004).
Le modèle est un système d'équations aux dérivées partielles. On suppose que le vol des moustiques suit un mouvement brownien de sorte qu'un terme classique de diffusion apparaît dans les équations qui gouvernent la densité de moustiques. Le modèle est non linéaire à cause des termes de « réaction » qui représentent la transmission de la maladie. Le modèle appartient ainsi à la famille des systèmes de réaction-diffusion. Ces systèmes ont été beaucoup étudiés dans le domaine des biomathématiques. Les premiers travaux remontent à Ronald A. Fisher (1937), qui s'intéressait déjà à l'onde de propagation d'un gène avantageux. Le sujet s'est beaucoup développé après ce travail pionnier avec des outils mathématiques plus sophistiqués (Smoller, 1981), avec des modèles plus complexes, et avec de nouveaux domaines d'application comme la morphogénèse ou la propagation géographique d'épidémies telles que la peste et la rage (Murray, 1989). Cependant, il semblerait que ce type de modèle n'ait pas encore été utilisé pour la propagation de la résistance à un médicament antipaludique. (Ruan et Xiao, 2004) étudie un système intégro-différentiel pour la propagation des épidémies de paludisme sans résistance.
Notre système d'équations de réaction-diffusion a des ondes progressives comme solutions, ce qui ressemble à la propagation géographique de la résistance à un médicament antipaludique (chloroquine, sulphadoxine-pyriméthamine ou autres). L'objectif principal de cet article est de trouver une expression pour la vitesse de propagation. On peut alors voir comment cette expression dépend des paramètres du modèle car certains d'entre eux peuvent être modifiés par décision, comme la fraction f de personnes traitées avec le médicament antipaludique. Le résultat donne une expression quantitative du fait qualitativement bien connu que la vitesse est une fonction croissante de f.
On espère que cette expression permettra de mieux comprendre le problème plus complexe de contrôle optimal, à savoir trouver le niveau de résistance au-dessus duquel des médicaments peu coûteux mais partiellement inefficaces doivent être remplacés par des médicaments plus coûteux mais efficaces. Cette question est d'un intérêt plus pratique et sujet à dispute (Attaran et coll., 2004).
La section 2 présente le modèle. On étudie les états d'équilibre et leur stabilité dans la section 3. Dans la section 4, on linéarise le système et l'on obtient une expression pour la vitesse des ondes progressives qui représentent la propagation de la résistance aux médicaments antipaludiques. Cette expression n'est valide que si la « conjecture linéaire » est correcte (Weinberger et coll., 2002 ; Lewis et coll., 2002). Des simulations numériques semblent confirmer la validité de cette conjecture pour notre modèle; les résultats sont discutés dans la section 5. D'un point de vue mathématique, le style reste informel et plus proche de celui utilisé dans (Murray, 1989). On peut espérer que des travaux futurs rempliront les trous dans la preuve.
Il y a deux variables indépendantes: le temps t et une variable spatiale unidimensionnelle x. La réduction à une dimension signifie que l'on s'intéresse à la propagation d'ondes planes le long d'une direction. Les inconnues sont:
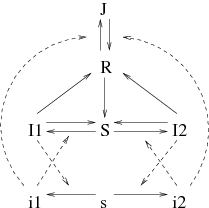
Le modèle est schématisé dans la figure 1. Il est très simplifié; de nombreux détails du cycle de transmission ont été omis. En particulier, on a omis les œufs et la période larvaire du cycle de vie des moustiques; à la place, on suppose que l'éclosion de nouveaux moustiques adultes compense la mortalité de sorte que la densité m des moustiques adultes est constante. Cependant, l'objectif ici est de garder le modèle assez simple pour pouvoir être analysé mathématiquement.

Pour simplifier les notations, \begin{align*} &a_1=k\, \pi_1\, \frac{m}{P}\, ,\quad a'_1=k \, \pi'_1\, ,\quad \bar{a}_1=k\, \bar{\pi}_1\, \frac{m}{P}\, ,\\ &a_2=k\, \pi_2\, \frac{m}{P}\, ,\quad a'_2=k\, \pi'_2\, ,\quad \bar{a}_2=k\, \bar{\pi}_2\, \frac{m}{P}\, . \end{align*} La formulation mathématique du modèle est un système d'équations aux dérivées partielles avec les hommes d'un côté, \begin{align} &\frac{\partial I_1}{\partial t}= a_1 \, S\, i_1 - b_1\, I_1\\ &\frac{\partial I_2}{\partial t}= a_2 \, S\, i_2 - b_2\, I_2\, , \tag{1}\\ &\frac{\partial R}{\partial t}= c\, I_1 + c\, I_2 - (e+\mu)\, R - \bar{a}_1\, R\, i_1 - \bar{a}_2\, R\, i_2 + \bar{b}\, J\, ,\\ &\frac{\partial J}{\partial t}= \bar{a}_1 \, R\, i_1+\bar{a}_2\, R\, i_2 - (\bar{b}+\mu)\, J\, , \end{align} et les moustiques de l'autre \begin{equation} \frac{\partial i_1}{\partial t}= a'_1 \, s\, I_1 - b'_1\, i_1 +d\, \frac{\partial^2 i_1}{\partial x^2}\, ,\quad \quad \frac{\partial i_2}{\partial t}= a'_2\, s\, I_2 - b'_2\, i_2 +d\, \frac{\partial^2 i_2}{\partial x^2}\, .\tag{2} \end{equation} Rappelons que \(S=1-I_1-I_2-R-J\) et \(s=1-i_1-i_2\).
Étudions tout d'abord les états d'équilibre qui ne dépendent pas de x. Il y a l'état d'équilibre trivial avec \[I_1=0, \quad I_2=0, \quad R=0, \quad J=0, \quad i_1=0,\quad i_2=0\, .\] Ceci correspond à la situation où le paludisme a été éradiqué. Sa stabilité dépend du signe des valeurs propres de la matrice obtenue en linéarisant le système près de (0,0,0,0,0,0), à savoir avec les inconnues dans l'ordre \(\,[i_1,I_1,R,J,i_2,I_2]\), \[\left ( \begin{array}{cccccc} -b'_1 & a'_1 & 0 & 0 & 0 & 0 \\ a_1 & -b_1 & 0 & 0 & 0 & 0\\ 0 & c & -(e+\mu) & \bar{b} & 0 & c \\ 0 & 0 & 0 & -(\bar{b}+\mu) & 0 & 0 \\ 0 & 0 & 0 & 0 & -b'_2 & a'_2 \\ 0 & 0 & 0 & 0 & a_2 & -b_2 \end{array} \right ).\] Les valeurs propres sont \(-(e+\mu)\), \(-(\bar{b}+\mu)\) et les valeurs propres des deux sous-matrices \[\left ( \begin{array}{cc} -b'_1 & a'_1\\ a_1 & -b_1 \end{array} \right ),\quad \left ( \begin{array}{cc} -b'_2 & a'_2 \\ a_2 & -b_2 \end{array} \right ) .\] Définissons la reproductivité des parasites sensibles et résistants par \[ \alpha_1=\frac{a_1\, a'_1}{b_1\, b'_1}\, ,\quad \alpha_2=\frac{a_2\, a'_2}{b_2\, b'_2}.\] L'état d'équilibre trivial est stable (toutes les valeurs propres sont négatives) si \(\alpha_1 < 1\) et \(\alpha_2 < 1\). L'état d'équilibre trivial est instable (au moins une valeur propre est positive) si \(\alpha_1 > 1\) ou si \(\alpha_2 > 1\).
Dans le cas \(\alpha_1 > 1\,\), il existe un autre état d'équilibre. On définit \[ \beta_1 = \frac{b'_1}{a'_1}\ ,\ \gamma_1 = \beta_1\, \frac{c}{e+\mu}\ ,\ \delta_1 = \gamma_1\, \frac{\bar{a}_1}{\bar{b}+\mu}\ ,\ \varepsilon_1 = \frac{\bar{a}_1}{\bar{b}+\mu} \, \frac{\mu}{e+\mu}\, . \] L'état d'équilibre est \[i_1=i_1^*, \quad I_1=I_1^*, \quad R=R_1^*, \quad J=J_1^*, \quad i_2=0, \quad I_2=0.\] \(\,i_1^*\) est la racine positive de \begin{equation} (\delta_1+\varepsilon_1+\beta_1\, \varepsilon_1)\, i_1^2 + \Bigl (1+\beta_1+\gamma_1+\varepsilon_1\, \bigl (\frac{1}{\alpha_1}-1\bigr )\Bigr )\, i_1 + \frac{1}{\alpha_1}-1 = 0\, , \end{equation} et \begin{equation} I_1^* = \beta_1\, \frac{i_1^*}{1-i_1^*}\, , \quad \quad R_1^*=\frac{\gamma_1\, I_1^*}{\beta_1\, (1+\varepsilon_1\, i_1^*)} \, ,\quad \quad J_1^*=\frac{\delta_1\, R_1^*\, i_1^*}{\gamma_1}\ . \end{equation} Cet état d'équilibre correspond à la situation où tous les parasites sont sensibles. Sa stabilité dépend du signe des valeurs propres de la matrice suivante, la linéarisation du système près de \((i_1^*,I_1^*,R_1^*,J_1^*,0,0)\), \[\left ( \begin{array}{cccccc} -(b'_1+a'_1\, I_1^*) & a'_1\, s_1^* & 0 & 0 & -a'_1\, I_1^* & 0 \\ a_1\, S_1^* & -(b_1+a_1\, i_1^*) & -a_1\, i_1^* & -a_1\, i_1^* & 0 & -a_1\, i_1^*\\ -\bar{a}_1\, R_1^* & c & -(e+\mu+\bar{a}_1\, i_1^*) & \bar{b} & -\bar{a}_2\, R_1^* & c \\ \bar{a}_1\, R_1^* & 0 & \bar{a}_1\, i_1^* & -(\bar{b}+\mu) & \bar{a}_2\, R_1^* & 0 \\ 0 & 0 & 0 & 0 & -b'_2 & a'_2\, s_1^* \\ 0 & 0 & 0 & 0 & a_2\, S_1^* & -b_2 \end{array} \right ),\] où par commodité \(s_1^*=1-i_1^*\) et \(S_1^*=1-I_1^*-J_1^*-R_1^*\). Les valeurs propres de la sous-matrice \(2\times 2\) \[\left ( \begin{array}{cc} -b'_2 & a'_2\, s_1^* \\ a_2\, S_1^* & -b_2 \end{array} \right ),\] qui sont aussi des valeurs propres de la matrice complète, sont \[-\frac{1}{2}\, (b_2+b'_2) \pm \frac{1}{2}\, \sqrt{(b_2+b'_2)^2-4\, [b_2\, b'_2 -a_2\, a'_2\, s_1^*\, S_1^*]}.\] Pour cet état d'équilibre, on voit facilement que \(s_1^*\, S_1^*=\frac{b_1\, b'_1}{a_1\, a'_1}\). Donc si \(\,\alpha_1 < \alpha_2\,\), une valeur propre de la sous-matrice \(2\times 2\) est positive, de sorte que l'état d'équilibre est instable.
De même, si \(\alpha_2 > 1\,\), il y a un autre état d'équilibre, défini par \(i_1=0\), \(I_1=0\), \(R=R_2^*\), \(J=J_2^*\), \(i_2=i_2^*\) et \(I_2=I_2^*\). Les formules sont les mêmes que ci-dessus, sauf que \(a'_1\) est remplacé par \(a'_2\), \(b'_1\) par \(b'_2\,\), et \(\bar{a}_1\) par \(\bar{a}_2\). \(\,\beta_1\), \(\gamma_1\), \(\delta_1\) et \(\varepsilon_1\) sont remplacés par \(\beta_2\), \(\gamma_2\), \(\delta_2\) et \(\varepsilon_2\,\). Cet état d'équilibre correspond à la situation où tous les parasites sont résistants. La linéarisation du système près de cet état d'équilibre montre qu'il est instable si \(\alpha_1 > \alpha_2\).
Ces résultats suggèrent que si \(\alpha_1 > 1\) et \(\alpha_2 > 1\), \((i_1^*,I_1^*,R_1^*,J_1^*,0,0)\) est stable si \(\alpha_1 > \alpha_2\,\), et \((0,0,R_2^*,J_2^*,i_2^*,I_2^*)\) est stable si \(\alpha_2 > \alpha_1\).
Remarque. Dans le modèle simplifié où l'immunité n'est pas prise en compte (\(c=0\), \(\bar{a}_1=0\)), on obtient \[i_1^*=\frac{1-1/\alpha_1}{1+\beta_1}\, ,\quad I_1^*=\frac{\alpha_1-1}{\alpha_1+1/\beta_1}\, .\] Ce sont les formules (14.5) et (14.6) dans (Anderson et May, 1991). \(\,1/\beta_1\,\) est « l'indice de stabilité de Macdonald ».
Lorsque des parasites résistants apparaissent quelque part, ils commencent à se propager à cause de la pression sélective du médicament. L'objectif de cette section est de calculer la vitesse de propagation en fonction des paramètres. On suppose que \(\alpha_2 > \alpha_1 > 1\). L'état d'équilibre trivial et l'état d'équilibre \((i_1^*,I_1^*,R_1^*,J_1^*,0,0)\) sont instables, tandis que l'état d'équilibre \((0,0,R_2^*,J_2^*,i_2^*,I_2^*)\,\) est stable. On étudie l'évolution d'une petite perturbation (à support compact) de l'équilibre homogène instable \(\,(i_1^*,I_1^*,R_1^*,J_1^*,0,0)\), de sorte que \(I_2(0,x) > 0\) (ou bien \(i_2(0,x) > 0\)) pour un certain x.
On s'attend à ce que cette petite perturbation se propage dans toutes les directions. Si l'on ne regarde qu'une direction de propagation, on observe une onde progressive. D'un point de vue mathématique, le système d'équations aux dérivées partielles (1)-(2) admet des solutions qui sont des ondes progressives s'il existe des fonctions positives d'une variable, encore appelées \(I_1\) \(I_2\), \(R\), \(J\), \(i_1\) et \(i_2\) avec un abus de notation, et \(v > 0\,\) dans le cas où l'onde se propage vers les x positifs, avec
| \(I_1(x,t)=I_1(x-v\, t)\), | \(I_2(x,t)=I_2(x-v\, t)\), | \(R(x,t)=R(x-v\, t)\), |
| \(J(x,t)=J(x-v\, t)\), | \(i_1(x,t)=i_1(x-v\,t)\), | \(i_2(x,t)=i_2(x-v\, t)\), |
avec les conditions au bord
| \(I_1(z) \to 0\), | \(I_2(z) \to I_2^*\), | \(R(z) \to R_2^*\), |
| \(J(z) \to J_2^*\), | \(i_1(z) \to 0\), | \(i_2(z) \to i_2^*\) |
si \(z\to -\infty\,\), et les conditions au bord
| \(I_1(z) \to I_1^*\), | \(I_2(z) \to 0\), | \(R(z) \to R_1^*\), |
| \(J(z) \to J_1^*\), | \(I_1(z) \to i_1^*\), | \(i_2(z) \to 0\) |
si \(z\to +\infty\). Remplaçons ces solutions d'onde progressive dans le système (1)-(2). On obtient \begin{eqnarray*} -v\, \frac{dI_1}{dz}&=& a_1\, (1-I_1-I_2-R-J)\, i_1 - b_1\, I_1,\\ -v\, \frac{dI_2}{dz}&=& a_2\, (1-I_1-I_2-R-J)\, i_2 - b_2\, I_2,\\ -v\, \frac{dR}{dz}&=& c\, I_1 + c\, I_2 - (e+\mu)\, R - \bar{a}_1\, R\, i_1 - \bar{a}_2\, R\, i_2 + \bar{b}\, J,\\ -v\, \frac{dJ}{dz}&=& \bar{a}_1 \, R\, i_1+ \bar{a}_2\, R\, i_2 - (\bar{b}+\mu)\, J, \end{eqnarray*} et \begin{eqnarray*} -v\, \frac{di_1}{dz}&=& a'_1\, (1-i_1-i_2)\, I_1 - b'_1\, i_1 +d\, \frac{d^2 i_1}{dz^2},\\ -v\, \frac{di_2}{dz}&=& a'_2\, (1-i_1-i_2)\, I_2 - b'_2\, i_2 +d\, \frac{d^2 i_2}{dz^2}. \end{eqnarray*} Ce système s'écrit aussi comme un système d'équations différentielles ordinaires du premier ordre si l'on définit \(j_1=\frac{di_1}{dz}\) et \(j_2=\frac{di_2}{dz}\). Les solutions qui sont des ondes progressives correspondent à des orbites positives de ce nouveau système qui relient les états d'équilibres [\(i_1=i_1^*\), \(j_1=0\), \(I_1=I_1^*\), \(R=R_1^*\), \(J=J_1^*\), \(i_2=0\), \(j_2=0\), \(I_2=0\)] et [\(i_1=0\), \(j_1=0\), \(I_1=0\), \(R=R_2^*\), \(J=J_2^*\), \(i_2=i_2^*\), \(j_2=0\), \(I_2=I_2^*\)]. On linéarise près de ce dernier état d'équilibre. On obtient la matrice \[ \left(\begin{array}{cccccccc} 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\ \frac{a'_1\, I_1^*+b'_1}{d} & \frac{-v}{d} & \frac{-a'_1\, s_1^*}{d} & 0 & 0 & \frac{a'_1\, I_1^*}{d} & 0 & 0 \\ \frac{-a_1\, S_1^*}{v} & 0 & \frac{a_1\, i_1^*+b_1}{v} & \frac{a_1\, i_1^*}{v} & \frac{a_1\, i_1^*}{v} & 0 & 0 & \frac{a_1\, i_1^*}{v} \\ \frac{\bar{a}_1\, R_1^*}{v} & 0 & \frac{-c}{v} & \frac{\bar{a}_1\, i_1^* + e+\mu}{v} & \frac{-\bar{b}}{v} & \frac{\bar{a}_2\, R_1^*}{v} & 0 & \frac{-c}{v}\\ \frac{-\bar{a}_1\, R_1^*}{v} &0 & 0 & \frac{-\bar{a}_1\, i_1^*}{v} & \frac{\bar{b}+\mu}{v} & \frac{-\bar{a}_2\, R_1^*}{v} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 0 & \frac{b'_2}{d} &\frac{-v}{d}& \frac{-a'_2\, s_1^*}{d}\\ 0 & 0 & 0 & 0 & 0& \frac{-a_2\, S_1^*}{v} & 0 & \frac{b_2}{v} \end{array} \right).\] Pour que les orbites soient positives près de cet état d'équilibre, il faut que les valeurs propres de la matrice soient toutes réelles. Considérons les valeurs propres de la sous-matrice \[ \left(\begin{array}{ccc} 0 & 1 & 0\\ \frac{b'_2}{d} &\frac{-v}{d}& \frac{-a'_2\, s_1^*}{d}\\ \frac{-a_2\, S_1^*}{v} & 0 & \frac{b_2}{v} \end{array} \right), \] qui sont aussi des valeurs propres de la matrice complète. Elles sont les racines du polynôme \(\chi(\lambda)=0\,\), avec \[\chi(\lambda)=-\lambda^3 + \Bigl (\frac{b_2}{v}-\frac{v}{d}\Bigr )\, \lambda^2 + \frac{b_2+b'_2}{d}\, \lambda + \frac{b_2\, b'_2}{v\, d}\, \Bigl (\frac{\alpha_2}{\alpha_1}-1\Bigr ).\]
Proposition 1. Il existe un unique \(\,v^* > 0\) pour lequel le polynôme \(\chi(\lambda)\) a une racine double lorsque \(v=v^*\). On définit \[y=\frac{b_2}{b'_2}\, ,\quad z=\frac{\alpha_2}{\alpha_1}-1.\] Le polynôme \begin{align*} F(X)=&\bigl [(1+y)^2 +4\, y\, z \bigr ] X^3+ 2 \bigl [ (1+y)^2\, (2+y) + 3\, (3+y)\, y\, z\bigr ] X^2 \\ &+ y^2\, \bigl [ (1+y)^2 -6\, z\, (3+y) - 27\, z^2\bigr ] X -4\, y^4\, z \end{align*} a une unique racine positive \(X^*\) et \[v^*=\sqrt{b'_2\, d\, X^*}.\]
Preuve. On définit \[\Lambda=\lambda-\frac{1}{3}\Bigl (\frac{b_2}{v}-\frac{v}{d}\Bigr ).\] On a alors \(\chi(\lambda)=-\chi_1(\Lambda)\), et \[\chi_1(\Lambda)=\Lambda^3+\mathcal{P}\, \Lambda + \mathcal{Q}\,,\] avec \(\mathcal{P}\) et \(\mathcal{Q}\,\) qui dépendent des paramètres et de v. Le polynôme \(\,\chi_1(\Lambda)\,\) a une racine double si et seulement si \(4 \mathcal{P}^3 + 27 \mathcal{Q}^2=0\). Réordonnons cette condition. On trouve qu'elle équivaut à \(F\Bigl (\frac{v^2}{b'_2\, d}\Bigr )=0\). \(\,F(X)\,\) a une unique racine positive. La preuve est donnée en appendice.
Dans le cas \(v < v^*\), le polynôme \(\chi(\lambda)\,\) a des valeurs propres complexes, de sorte que le système ne peut avoir d'onde progressive. Cette situation, comparée aux études sur les systèmes de réaction-diffusion dans lesquelles c'est la vitesse minimale qui est selectionnée par le système (Murray, 1989), suggère ceci:
Conjecture. La vitesse des ondes progressives est \(v^*\).
Une conjecture de ce genre est généralement appelée une « conjecture linéaire » pour les systèmes de réaction-diffusion, puisqu'on y aboutit en linéarisant le système non linéaire d'équations aux dérivées partielles près d'un équilibre. D'autres études (Hosono, 1998) ont montré que pour certains modèles, cette conjecture n'est correcte que dans une certaine plage de valeurs des paramètres. (Weinberger et coll., 2002) a donné des conditions suffisantes pour que la « conjecture linéaire » soit valable pour des systèmes coopératifs. Dans (Lewis et coll., 2002), ces conditions sont utilisées pour un système compétitif qui peut être transformé par un changement d'inconnues en un système coopératif. Bien que notre modèle de compétition puisse aussi être transformé en un système coopératif comme dans (Lewis et coll., 2002), les conditions suffisantes de (Weinberger et coll., 2002) appliquées ici deviennent très compliquées.
La figure 2 montre la vitesse sans dimension \(v^*/\sqrt{b'_2\, d}=\sqrt{X^*}\) en fonction de \(\alpha_2/\alpha_1\) pour différentes valeurs de \(y=b_2/b'_2\). La vitesse est calculée en cherchant numériquement les racines de l'équation polynomiale du troisième degré \(F(X)=0\), pour en tirer la seule racine positive. Noter que \(v^*/\sqrt{b'_2\, d}\) semble être une fonction croissante de \(\alpha_2/\alpha_1\). Avec \(\,y\ll 1\,\), on obtient l'expression approchée \[X^*\mathop{\sim}_{y\to 0} \frac{-1+18\, z +27\, z^2 + \sqrt{(-1+18\, z+27\, z^2)^2+64\, z}}{8}\, y^2\, .\] La figure montre aussi le résultat de simulations numériques du système non linéaire d'équations aux dérivées partielles. On tronque l'espace \(-L < x < L\). On démarre d'une condition initiale qui est une fonction en escalier
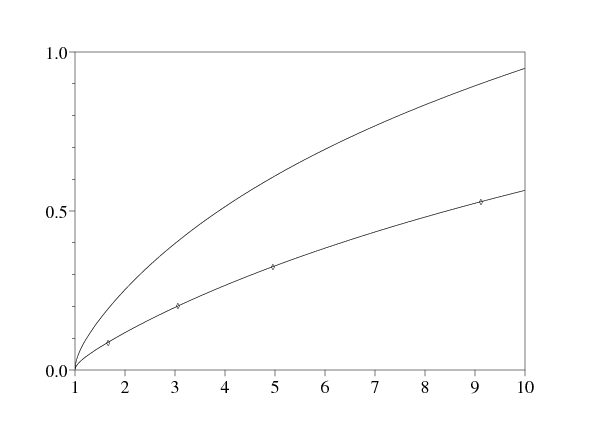
Ainsi les simulations tendent à confirmer la validité de la conjecture linéaire pour notre modèle ou au moins pour une certaine plage de valeurs des paramètres contenant les valeurs utilisées dans les simulations.
Les caractéristiques principales du modèle sont:
Le résultat qualitatif, qui dit que la résistance se propage plus vite dans les zones avec un meilleur accès aux médicaments, est conforme aux études de terrain. Au Sénégal par exemple, un pays avec une population d'environ dix millions d'habitants, il y a environ un million de cas de paludisme chaque année, qui provoquent 8000 décès. La résistance à la chloroquine est apparue en 1988 à Dakar, la capitale. Elle a augmenté et s'est propagée depuis (Sokhna et coll., 1997 ; Trape et coll., 2003). À Mlomp, où un programme de distribution de la chloroquine a été conduit pendant de nombreuses années (\(f\simeq 100\%\)), l'émergence de la résistance à la chloroquine a été particulièrement rapide: pas de résistance en 1989, 10% en 1990, 51% en 1991, 71% en 1997. Sans programme de ce genre, l'émergence a été plus lente à Bandafassi : premiers cas en 1993, 12% en 1994, 16% en 1995.
Ces données peuvent servir de comparaison avec notre modèle. Le tableau 1 montre des ordres de grandeur des paramètres nécessaires pour calculer la vitesse (la mortalité a été négligée). Noter que l'infectiosité apparaît plus tôt (\(T_2 < T_1\)) chez les hommes infectés par les parasites résistants, comme suggéré dans les expériences résumées dans (Koella, 1998). Pour que \(\alpha_2/\alpha_1 < 1\) si f=0, les moustiques infectés par des parasites résistants doivent avoir une mortalité supérieure (\(b'_2 > b'_1\)). La mortalité des moustiques infectés est aussi supérieure à celle des moustiques non infectés (\(\simeq \mbox{0,1}\) jour\(^{-1}\)) tirée de (Anderson et May, 1991). On estime le coefficient de diffusion par la formule \(\,d=L^2/t\), où L≈ 1 km est le rayon de la zone qu'un moustique peut explorer pendant une journée.
| paramètre | symbole | estimation |
| mortalité des moustiques \(i_1\) | \(b'_1\) | 0,12 jour\(^{-1}\) |
| mortalité des moustiques \(i_2\) | \(b'_2\) | 0,2 jour\(^{-1}\) |
| taux de guérison des non immunisés | \(b\) | 0,005 jour\(^{-1}\) |
| taux de guérison avec le médicament | \(\hat{b}\) | 0,1 jour\(^{-1}\) |
| taux d'acquisition de l'immunité | \(c\) | 0,003 jour\(^{-1}\) |
| période de latence dans les moustiques | \(T'_1\), \(T'_2\) | 10 jours |
| période de latence chez les hommes \(I_1\) | \(T_1\) | 10 jours |
| période de latence chez les hommes \(I_2\) | \(T_2\) | 8 jours |
| diffusion des moustiques | \(d\) | 1 km\(^2\)/jour |
Avec les estimations du tableau 1, on a \(y=b_2/b'_2 = \mbox{0,04}\). Si f=100%, alors \(\alpha_2/\alpha_1 \simeq \mbox{9,1}\) et \(v^*\simeq 86\,\) km/an. Si f=30% (une estimation moyenne pour le Sénégal (OMS et UNICEF, 2003)), alors \(\alpha_2/\alpha_1 \simeq \mbox{1,66}\) et \(v^*\simeq 14\,\) km/an. Ainsi, avec ces choix de paramètres, la résistance se propage six fois plus vite dans une zone avec f=100% que dans une zone avec f=30%. Le seuil \(f^*\), qui correspond à \(\alpha_1=\alpha_2\), au-dessus duquel la résistance peut se propager est 17,6%, une estimation plus raisonnable que les 89% de (Koella et Antia, 2003, figure 3).
Enfin il faut insister sur le fait que notre modèle n'est qu'un pas dans le développement de modèles spatiaux réalistes de la diffusion de la résistance aux médicaments antipaludiques. On doit regarder les valeurs numériques précises sans oublier les nombreuses hypothèses simplificatrices du modèle; certaines pourraient être relâchées dans un travail à venir. Une autre direction serait d'inclure des inhomogénéités spatiales entre les villes et les campagnes, ou des changements temporels de la population humaine totale et des densités de moustiques. Pour la densité de moustiques en particulier, on n'a pas tenu compte des variations saisonnières, un facteur important au Sénégal, où la densité de moustiques dépend beaucoup de la pluviométrie.
\(F(X)=0\,\) a une unique racine positive. Cela découle d'un calcul élémentaire, en utilisant \(y > 0\) et \(z > 0\) (cette dernière inégalité équivaut à \(\alpha_2 > \alpha_1\)). En effet, si \[F(X) = c_3 X^3 + c_2 X^2 + c_1 X+c_0,\] on a alors \(c_3 > 0\), \(c_2 > 0\), \(c_0 < 0\,\) et \[F'(X)=3\, c_3\, X^2 + 2\, c_2\, X + c_1.\] De simples inégalités montrent, en utilisant que \(y > 0\) et \(z > 0\), que le discriminant \(c_2^2-3\, c_1\, c_3\) de \(F'(X)\) est positif. \(\,X_1\) et \(X_2\) sont les racines de \(F'(X)\). On a alors \[X_1+X_2=-2\, c_2/(3\, c_3) < 0,\quad X_1\, X_2= c_1/(3\, c_3).\]
Dans le cas \(\,c_1\geq 0\,\), on a \(X_1\, X_2\geq 0\,\). On a donc \(\,X_1 < 0\) et \(X_2\leq 0\). Dans ce cas, \(\,F(X)\) est monotone pour \(X > 0\) avec \(F(0)=c_0 < 0\), \(F'(0)=c_1\geq 0\) et \(F(X)\to +\infty\) si \(X\to +\infty\). Ainsi il y a une unique racine positive de \(F(X)\).
Dans le cas \(\,c_1 < 0\,\), on a \(X_1\, X_2 < 0\,\). On a donc \(\,X_1 < 0\) et \(X_2 > 0\). \(\,F'(X)\) change de signe seulement une fois quand \(X > 0\). Mais \(\,F(0)=c_0 < 0\), \(F'(0)=c_1 < 0\) et \(F(X)\to +\infty\) si \(X\to +\infty\). Donc il y a une unique racine positive de \(\,F(X)\) dans ce cas aussi.
Nicolas Bacaër remercie le département de mathématiques de l'université Cheikh Anta Diop à Dakar, où une partie de ce travail a été effectuée.