Bull. Math. Biol. 68 (2006) 525-550
Nicolas Bacaër
Institut de recherche pour le développement
Bondy, France
nicolas.bacaer@ird.fr
Xamxinur Abdurahman
Département de mathématiques et sciences des systèmes
Université du Xinjiang, Urumqi, Chine
Jianli Ye
Centre pour la surveillance de la santé publique, CCDC, Pékin, Chine
Cet article présente un modèle mathématique de l'épidémie de VIH/SIDA à Kunming, la capitale provinciale du Yunnan, en Chine. La population est divisée en plusieurs groupes, avec des individus qui peuvent changer de groupe. On considère deux modes de transmission du VIH: le partage des seringues entre utilisateurs de drogue et la transmission sexuelle entre les travailleuses du sexe et leurs clients. Le modèle inclut des utilisateurs de drogue qui sont aussi des clients et des utilisatrices de drogue qui sont des travailleuses du sexe. Les groupes sont scindés en deux sous-groupes, à risque ou protégé, suivant l'utilisation de préservatifs et le partage de seringues. On formule un système d'équations aux dérivées partielles pour décrire la propagation de la maladie. Pour les simulations, on ajuste les paramètres autant que possible aux données disponibles sur Kunming. On présente certaines propriétés mathématiques du modèle, en particulier le seuil épidémique \(R_0\,\) qui détermine l'objectif des interventions de santé publique. Quoique le modèle combine deux modes de transmission du VIH, l'approximation suivante semble assez bonne : \(\,R_0\simeq \max \{R_0^{\mathrm{drogue}},R_0^{\mathrm{sexe}}\}\,\), avec des formules explicites pour \(R_0^{\mathrm{drogue}}\) et \(R_0^{\mathrm{sexe}}\). Les niveaux critiques d'utilisation des seringues propres et des préservatifs, nécessaires pour arrêter à la fois la transmission parmi les utilisateurs de drogue et la transmission sexuelle, peuvent donc être déterminés indépendamment l'un de l'autre.
L'épidémie de VIH/SIDA s'est développée assez vite au cours des dernières années en Chine. À la fin de l'année 2003, on estimait que le nombre cumulé de personnes infectées par le VIH était d'environ 840000 [44]. À l'échelle nationale, l'utilisation de drogue, la collecte de sang non sécurisée et la transmission sexuelle étaient par ordre décroissant les principales voies de transmission. Mais il y a des différences entre les provinces. Pour la transmission du VIH entre utilisateurs de drogue, c'est la province du Yunnan qui semble la plus touchée. Le Yunnan est proche du Myanmar, un pays producteur d'héroïne. Certaines estimations suggèrent que 100000 personnes sont actuellement infectées dans cette province [1]. L'épidémie parmi les utilisateurs de drogue se propage vers d'autres groupes à risque tels que les travailleuses du sexe et leurs clients, puisque certains utilisateurs de drogue sont aussi des clients ou des travailleuses du sexe. Dans le présent article, on essaye de reproduire la dynamique de l'épidémie à Kunming, la capitale provinciale du Yunnan. On développe un modèle épidémique couplant la transmission du VIH par le partage de seringues et par les rapports sexuels commerciaux.
La première étape a consisté à rassembler les données disponibles relatives à l'épidémie de VIH/SIDA à Kunming. Voici ce que l'on a trouvé de plus utile:
| année | nouveaux cas | total des cas | prévalence chez les drogués (%) | prévalence chez les travailleuses du sexe (%) | prévalence chez les clients (%) |
| 1990 | 4\(^g\) | 4\(^g\) | 0,6\(^g\) | 0\(^g\) | 0\(^g\) |
| 1991 | 5\(^g\) | 9\(^g\) | 0,1\(^g\) | 0,1\(^g\) | 0,1\(^g\) |
| 1992 | 5\(^g\) | 14\(^g\) | 0\(^h\); 0,1\(^g\) | 0,1\(^g\) | 0,1\(^g\) |
| 1993 | 6\(^g\) | 20\(^g\) | 0\(^h\); 0,2\(^g\) | 0,1\(^g\) | 0,1\(^g\) |
| 1994 | 4\(^g\) | 24\(^g\) | 0\(^{a-g-h}\) | 0\(^c\); 0,3\(^g\) | 0,1\(^g\) |
| 1995 | 24\(^g\) | 48\(^g\) | 0,7\(^{a-i}\); 0,8\(^h\); 1,4\(^g\) | 0,3\(^g\); 0,5\(^{a-c}\); 0,7\(^i\) | 0\(^c\); 0,2\(^i\) |
| 1996 | 189\(^g\) | 237\(^g\) | 9,3\(^{a-h}\); 14,0\(^g\) | 0,8\(^{a-g}\); 1,5\(^c\) | 0\(^c\); 0,1\(^g\) |
| 1997 | 26,7\(^g\); 27,5\(^h\) | 1,5\(^c\); 1,9\(^g\) | 0\(^c\); 1,6\(^g\) | ||
| 1998 | 23,4\(^{b-h}\) | 2,4\(^c\) | 0,3\(^c\) | ||
| 1999 | 384\(^f\) | 1251\(^f\) | 24,4\(^b\); 24,7\(^f\) | 2,2\(^{b-c}\); 2,9\(^f\) | 1,1\(^c\); 1,3\(^f\) |
| 2000 | 2,9\(^c\) | ||||
| 2001 | 165\(^e\) | 30,0\(^e\) | 2,0\(^{c-e}\) | 1,8\(^{c-e}\) | |
| 2002 | 1433\(^g\) | 1,3\(^c\) | 0,3\(^c\) | ||
| 2003 | 226\(^d\) | 18,6\(^d\) | 2,5\(^{c-d}\) | 0,8\(^{c-d}\) |
| année | 1993 | 1995 | 1998 | 1999 | 2000 | 2002 |
| population (millions) | 1,608 | 1,645 | 1,731 | 2,063 | 2,108 | 2,200 |
La seconde étape a consisté à développer un modèle mathématique de la structure de la population et de la transmission du VIH à Kunming, avec deux objectifs contradictoires :
Parmi les études similaires qui se sont focalisées sur les simulations, quatre sont d'un intérêt particulier. Les deux premières [48, 7] ont essayé de prédire le futur de l'épidémie au Yunnan. La troisième [32] a essayé la même chose mais pour l'ensemble de la Chine. La quatrième [8] a utilisé un modèle avec des données de différentes villes du sud-est asiatique telles que Jakarta. La première étude utilise un modèle linéaire très simple, qui ne peut prédire que la croissance exponentielle. La seconde utilise le logiciel EPP développé par ONUSIDA pour simuler les épidémies à transmission sexuelle généralisée. Noter cependant que l'épidémie dans le Yunnan est encore concentrée dans les groupes à risque tels que les utilisateurs de drogue. La troisième étude utilise un modèle plus sophistiqué, mais toujours sans partage des seringues, et l'applique avec des données moyennes nationales.
Pour ces trois premières études, les niveaux géographiques auxquels ils opèrent cachent de nombreuses hétérogénéités, soit entre les provinces de Chine [44], soit même d'une ville à l'autre à l'intérieur de la même province. Au Yunnan, la distance à la frontière du Myanmar et aux routes où passe le trafic de drogue est un élément clé. C'est ce qui nous a conduit à ne considérer que la ville de Kunming et non une zone plus large.
Notre étude est en plusieurs points plus proche de la quatrième étude [8], bien que l'on considère moins de voies de transmission du VIH. En particulier, on a gardé l'idée que dans les modèles de population avec plusieurs groupes, les individus doivent pouvoir changer de groupe. Par exemple, les travailleuses du sexe travaillent souvent pour une période de temps bien plus courte que la période moyenne d'incubation du SIDA. Il faut d'ailleurs mentionner le débat autour de toutes ces simulations, notamment au sujet de leur capacité prédictive [43, 14, 16, 34]. Un autre inconvénient de ces simulations est qu'elles donnent souvent peu d'indication sur le seuil épidémique et sur le comportement à long terme du modèle, le type d'information nécessaire pour fixer des objectifs de santé publique.
Parmi les études mathématiques, on a restreint notre attention à celles avec les caractéritiques suivantes, proches de [28] :
Dans notre article, on n'étudie pas les propriétés mathématiques du modèle aussi précisément que dans certains travaux cités ci-dessus; on limite notre attention à la reproductivité et à quelques autres propriétés élémentaires. On accorde cependant plus d'attention à l'estimation des paramètres à partir des données. En résumé, comparé à l'un des modèles les plus utilisés pour les épidemies de VIH/SIDA concentrées dans les groupes à risque en Asie, le modèle de [8], notre modèle présente l'avantage de conduire à une expression pour la reproductivité tout en gardant un certain réalisme.
Dans le § 2, on introduit le modèle mathématique pour un nombre arbitraire de groupes et avec des paramètres qui peuvent dépendre du temps. Le § 3 discute de certaines propriétés mathématiques du modèle lorsque les paramètres ne dépendent pas du temps, ou de manière plus réaliste lorsque les paramètres se stabilisent après un certain temps (c'est bien sûr une abstraction mathématique puisqu'on ne ne peut guère dire que la société chinoise est à l'équilibre de nos jours, même dans une province périphérique telle que le Yunnan). On montre que la reproductivité, qui détermine les objectifs des interventions de santé publique, est telle que \(\,R_0\geq \max \{R_0^{\mathrm{drogue}},\, R_0^{\mathrm{sexe}}\}\). \(\,R_0^{\mathrm{drogue}}\) et \(R_0^{\mathrm{sexe}}\,\) sont les reproductivités facilement calculables associées au partage des seringues et à la transmission sexuelle. Ces reproductivités sont données par le rayon spectral de matrices de rang 1 ou 2. Le § 4 spécialise le modèle au cas de dix-huit groupes et discute des matrices de contact et de changement de groupe. Le § 5 calcule les reproductivités \(\,R_0^{\mathrm{drogue}}\) et \(R_0^{\mathrm{sexe}}\,\) pour ce modèle particulier. Enfin le § 6 estime les paramètres avec les données disponibles pour Kunming et montre une simulation de l'année 1994 jusqu'à la fin de 2004. La conclusion analyse numériquement la dépendance de la reproductivité par rapport au pourcentage d'utilisation de préservatifs et au taux de partage des seringues pour les utilisateurs de drogue. L'approximation suivante semble assez bonne \[R_0\simeq \max \{R_0^{\mathrm{drogue}},\, R_0^{\mathrm{sexe}}\}.\] Les niveaux critiques d'utilisation des seringues propres et des préservatifs, nécessaires pour arrêter à la fois la transmission parmi les utilisateurs de drogue et la transmission sexuelle, peuvent ainsi être déterminés indépendamment.
On définit
Pour les termes qui représentent la transmission hétérosexuelle, considérons un homme sain du groupe i. Supposons que le mélange soit proportionnel. La probabilité de rencontrer une travailleuse du sexe du groupe j est \(\,a_j\, N_j / \sum_k a_k\, N_k\). Dans ce cas, la probabilité de ne pas utiliser de préservatif est \(1-c_{ij}\). La probabilité que la femme soit déjà infectée est \(\,I_j/N_j\). La probabilité que la transmission du VIH ait lieu de la femme vers l'homme est \(\,\pi_2\). Donc la probabilité d'infection sexuelle par unité de temps d'un homme sain du groupe i est le produit de tous ces facteurs, comme dans (1) et (2).
Considérons maintenant une femme saine du groupe i. Cela peut être une travailleuse du sexe ou une femme droguée se prostituant à l'occasion pour s'acheter de la drogue. Avec un mélange proportionnel, le nombre de clients qu'elle aura par jour est le quotient de la demande des hommes et de l'offre des travailleuses du sexe \[\frac{\sum_k A_k\, N_k}{\sum_k a_k\, N_k}\, .\] La probabilité qu'un client appartienne au groupe j est \(\,A_j\, N_j / \sum_k A_k\, N_k\). Dans ce cas, la probabilité de ne pas utiliser de préservatif est \(\,1-c_{ji}\). La probabilité que le client soit déjà infecté est \(\,I_j/N_j\). La probabilité pour que la transmission du HIV se fasse de l'homme vers la femme est \(\pi_1\). Donc la probabilité d'infection sexuelle par unité de temps d'une femme saine du groupe i est le produit de tous ces facteurs, comme dans (1) et (2).
On a supposé que tous les parameters dépendent a priori du temps pour refléter de possibles changements de comportements ou un accès accru aux médicaments antirétroviraux. \(\pi_1\) et \(\pi_2\,\) peuvent aussi dépendre du temps si l'on veut prendre en compte l'augmentation d'autres infections sexuellement transmissibles, qui favorisent la transmission du VIH. La dépendance temporelle de π peut refléter par exemple un accroissement de l'usage de seringues propres parmi les utilisateurs de drogue.
Considérons le modèle de la section 2, mais avec des paramètres indépendants du temps. Introduisons du vocabulaire qui simplifiera les énoncés. Considérons les n groupes comme les noœuds d'un graphe mathématique avec deux types d'arêtes:
\((H_1)\,\) \(\, \forall i=1\ldots n\), \(\Lambda_i > 0\) ou il existe un chemin d'arêtes de migration \((j_0,\ldots,j_{p})\) avec \(\Lambda_{j_0} > 0\) et \(j_p=i\).Techniquement, la seconde partie peut s'écrire: \[\exists \, p\geq 1, \quad \exists (j_0,\ldots,j_{p}), \quad \forall q=1\ldots p, \,\alpha_{j_q\gets j_{q-1}} > 0, \quad \Lambda_{j_0} > 0,\quad j_p=i.\] L'hypothèse (\(H_1\)) signifie simplement que les individus du groupe i « viennent de quelque part »: soit ils sont entrés dans la population directement dans le groupe i, ou ils sont entrés dans un groupe \(\,j_0\) et sont passés par les groupes \(j_1,\ldots,j_{p-1}\) avant d'atteindre le groupe \(j_p=i\).
Proposition 1 L'équilibre sans maladie est donné par \(S^0=\mathbb{A}^{-1} \Lambda\) et \(I^0=0\). De plus, on a \(\,S^0_i > 0\,\forall i=1\ldots n\).
Preuve. Noter tout d'abord que la matrice \(\,\mathbb{A}\,\) est à diagonale strictement dominante avec des éléments hors diagonale positifs ou nuls. Donc elle est inversible et son inverse est une matrice à coefficients ≥0 [6]. Avec \(\,\Lambda\geq 0\) (c'est-à-dire \(\Lambda_i\geq 0\,\forall i\)), on a \(\,S^0=\mathbb{A}^{-1} \Lambda\geq 0\). On choisit i et \((j_0,\ldots,j_{p-1})\) comme dans l'hypothèse (\(H_1\)). L'équation (2) avec \(\,I=0\) conduit à \[0=\Lambda_k - \Bigl (\alpha_k+\sum_{j\neq k} \alpha_{j\gets k} \Bigr )\, S^0_k + \sum_{j\neq k} \alpha_{k\gets j}\, S^0_j, \quad \forall \, k=1\ldots n .\] On suppose par l'absurde \(\,S_i^0=0\). Avec l'équation ci-dessus où k=i, on obtient \(\Lambda_i=0\) et \(S^0_{j_{p-1}}=0\). Par itération, on prend \(k=j_{p-1},\ldots ,k=j_0\), on arrive finalement à \(\Lambda_{j_0}=0\) et \(S^0_{j_0}=0\). Ceci contredit \(\,\Lambda_{j_0} > 0\).
Avant de présenter la conjecture principale concernant les états d'équilibre, étudions la stabilité de l'équilibre sans maladie. On définit \(\,S=S^0 + s\) et \(I=i\). Linéarisons les équations (3)-(4). On obtient \[ \frac{\partial i}{\partial t}+\frac{\partial i}{\partial x} = -\mathbb{A}\, i(t,x) -\gamma(x)\, i(t,x)\, ,\quad i(t,0)\simeq \mathrm{diag}(S^0)\, \mathbb{B}(S^0) \int_0^\infty i(t,x)\, dx. \] \(\mathrm{diag}(S^0)\) est la matrice diagonale construite avec les éléments du vecteur \(S^0\). Pour un tel système (voir par exemple [5]), on sait que la stabilité dépend du rayon spectral \(R_0\) de la matrice \begin{equation} \Omega=\mathrm{diag}(S^0)\,\mathbb{B}(S^0) \int_0^\infty e^{-\mathbb{A} t}\, e^{- \int_0^t \gamma(x)\, dx}\, dt \tag{5} \end{equation} selon que \(R_0 < 1\) ou \(R_0 > 1\). Cela s'interprète de la façon suivante. \(P_{ij}(t)\,\) est la probabilité pour un individu d'être dans le groupe i au temps t sachant qu'il a été infecté au temps t=0 et qu'il appartenait alors au groupe j. La matrice \(\,P(t)\) est la solution de \begin{equation}\tag{6} \frac{dP}{dt} = -\mathbb{A}\, P(t) - \gamma(t)\, P(t)\, ,\quad P(0)=\mathbf{1}\, . \end{equation} \(\mathbf{1}\,\) est la matrice identité de taille n. Noter que \[P(t)=e^{-\mathbb{A}t} \, e^{-\int_0^t \gamma(x)\, dx}.\] On définit \(\,T_{ij}\,\) l'espérance du temps qu'un porteur du VIH passera dans le groupe i sachant qu'il appartenait au groupe j au moment de l'infection. On a alors \[T=\int_0^\infty P(t)\, dt.\] On voit donc que \[\Omega_{ij}=S_i^0 \sum_{k=1}^n \mathbb{B}_{ik}(S^0)\, T_{kj}.\] Mais \(\,S_i^0\, \mathbb{B}_{ik}(S^0)\,\) est le nombre d'individus dans le groupe i infectés par unité de temps par un individu infecté dans le groupe k juste après son introduction dans la population sans maladie à l'équilibre. \(\,\Omega_{ij}\,\) est donc l'espérance du nombre d'individus dans le groupe i au moment de l'infection qu'un individu qui appartenait au groupe j au moment de l'infection infectera au cours de sa vie, en supposant que la population reste proche de son état d'équilibre sans maladie. Autrement dit, Ω est la « matrice de prochaine génération » de [17, p.74].
Présentons maintenant une conjecture inspirée du travail de [38] pour le cas particulier d'une matrice diagonale \(\mathbb{A}\). La preuve présentée dans cette référence peut sans doute être généralisée au cadre présent, mais un travail supplémentaire est nécessaire pour le vérifier. Dans tout ce qui suit, on suppose que l'ensemble des groupes essentiels est connexe.
Conjecture. Si le rayon spectral de la matrice Ω est tel que \(R_0 < 1\), alors l'état d'équilibre sans maladie \((S^0,I^0)\,\) est le seul état d'équilibre et c'est un attracteur global. Il y a deux états d'équilibre si \(\,R_0 > 1\,\): l'état d'équilibre sans maladie et un équilibre endémique \((S^*,I^*)\) avec \(I^*\neq 0\). Dans ce deuxième cas, l'état d'équilibre endémique est un attracteur global pour toute condition initiale avec \(\,I_k\neq 0\,\) pour au moins un groupe k qui est une source ou un groupe essentiel. L'état d'équilibre sans maladie reste un attracteur pour toutes les autres conditions initiales.
Les propositions suivantes donnent quelques informations sur l'état d'équilibre endémique:
Proposition 2. Pour l'état d'équilibre endémique \(\,(S^*,I^*)\), on a \[I^*(x)=e^{-\mathbb{A} x}\,e^{- \int_0^x \gamma(t)\, dt}\, I^*(0).\] Les vecteurs \(S^*\) et \(I^*(0)\) sont des solutions \(\geq 0\) et \(\neq 0\) du système \begin{eqnarray} S^*&=&\mathbb{A}^{-1}(\Lambda-I^*(0))\, ,\tag{7}\\ I^*(0)&=&S^* \odot \Biggl [\mathbb{B}(N^*) \int_0^\infty e^{-\mathbb{A} t}\, e^{- \int_0^t \gamma(x)\, dx}\, dt \,I^*(0)\Biggr ]\, ,\tag{8} \end{eqnarray} avec \(N^*=S^*+\int_0^\infty I^*(x)\, dx\).
Ces équations s'obtiennent par simple intégration et substitution dans le système (2)-(3)-(4). Démontrer l'existence et l'unicité de l'état d'équilibre endémique dans cette conjecture équivaut à démontrer l'existence et l'unicité d'une solution \(\,(S^*,I^*(0))\) ≥0 et ≠0 du système (7)-(8).
Proposition 3. \(\forall \, i=1,\ldots,n,\quad S_i^* > 0\).
Preuve. On choisit i et \(\,(j_0,\ldots,j_{p-1})\) comme dans l'hypothèse (\(H_1\)). On a \(\, \forall\, k=1,\ldots,n\), \begin{eqnarray} &&0=\Lambda_k - \Bigl (\alpha_k+\sum_{j\neq k} \alpha_{j\gets k} \Bigr )\, S_k^* + \sum_{j\neq k} \alpha_{k\gets j}\, S_j^* - I_k^*(0)\, ,\tag{9}\\ &&I_k^*(0)=S_k^* \sum_j \mathbb{B}_{kj}(N^*) \int_0^\infty I_j^*(x)\, dx\, .\tag{10} \end{eqnarray} On suppose par l'absurde \(\,S_i^*=0\). Avec (10) où k=i, on a \(I_i^*(0)=0\). Avec (9) où k=i, on obtient \(\Lambda_i=0\) et \(S^*_{j_{p-1}}=0\). Par itération, en prenant successivement \(k=j_{p-1},\ldots, k=j_0\), on arrive finalement à \(\Lambda_{j_0}=0\) et \(S_{j_0}=0\). Ceci contredit \(\Lambda_{j_0} > 0\).
Proposition 4 Si le groupe i est un groupe essentiel, alors \(\,I^*_i(x) > 0\,\) pour tout x. Si le groupe i est un groupe puits, alors \(\,I^*_i\neq 0\) mais \(I^*_i(0)=0\). Si le groupe i est ni un groupe essentiel ni un puits, alors \(I^*_i(x)= 0\,\) pour tout x.
Preuve. Si le groupe i n'est pas un groupe essentiel, alors \(B_{ij}(N^*)=0\,\) pour tout j. On a donc \(\,I^*_i(0)=0\,\) à cause de (10) avec \(k=i\). On a \[I^*(x)=e^{-\mathbb{A}\, x}\, e^{-\int_0^x \gamma(t)\, dt}\, I^*(0)\] et \(I^*\neq 0\). Donc il existe un groupe essentiel j avec \(\,I^*_j(0) > 0\). Pour un autre groupe essentiel i, considérons différentes situations:
Considérons un groupe i qui est un puits. Il y a un groupe essentiel j et un chemin d'arêtes de migration \(i_1,\ldots,i_p\) avec \(i_1=i\) et \(i_p=j\). On utilise (11) avec i remplacé successivement par \(i_{p-1},\ldots,i_1\) et \(I^*_j(x) > 0\,\) pour tout x. On obtient \(\,I_i^*\neq 0\).
On suppose maintenant que les numéros des groupes sont ordonnés
Proposition 5 On définit \[\Omega^{\mathrm{drogue}}=\mathrm{diag}(S^0)\,\mathbb{B}^{\mathrm{drogue}}(S^0) \int_0^\infty e^{-\mathbb{A} t}\, e^{- \int_0^t \gamma(x)\, dx}\, dt\] et \[\Omega^{\mathrm{sexe}}=\mathrm{diag}(S^0)\,\mathbb{B}^{\mathrm{sexe}}(S^0) \int_0^\infty e^{-\mathbb{A} t}\, e^{- \int_0^t \gamma(x)\, dx}\, dt.\] \(R_0^{\mathrm{drogue}}\) est le rayon spectral de la matrice \(\Omega^{\mathrm{drogue}}\). \(R_0^{\mathrm{sexe}}\) est le rayon spectral de la matrice \(\Omega^{\mathrm{sexe}}\). On a alors \[R_0\geq \max \{R_0^{\mathrm{drogue}}, R_0^{\mathrm{sexe}}\}.\]
Preuve. Rappelons que si deux matrices \(\,M\) et \(M'\) à coefficients ≥0 sont telles que \(M\leq M'\), c'est-à-dire \(M_{ij}\leq M_{ij}'\,\) pour tout i et j, alors les rayons spectraux sont tels que \(\,R_0(M)\leq R_0(M')\) [23, § 8.1.18]. \(\,e^{-\mathbb{A} x}\,\) est une matrice à coefficients ≥0. \(\Omega^{\mathrm{drogue}}\) et \(\Omega^{\mathrm{sexe}}\,\) sont donc aussi des matrices à coefficients ≥0. Avec \(\,\Omega=\Omega^{\mathrm{sexe}}+\Omega^{\mathrm{drogue}}\), on a \(\Omega \geq \Omega^{\mathrm{sexe}}\) et \(\Omega \geq \Omega^{\mathrm{drogue}}\,\), d'où la conclusion.
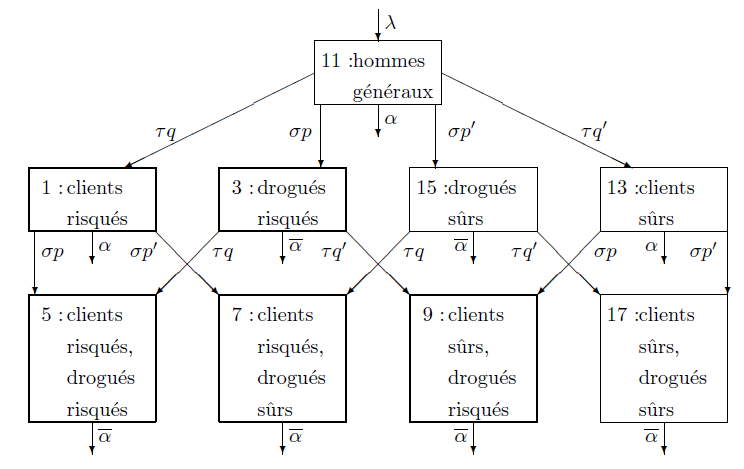
Retournons au modèle avec des paramètres qui peuvent dépendre du temps. On a déjà en tête la situation de Kunming et le type de données disponibles pour faire quelques simplifications. La population considérée comprend des hommes et des femmes entre 18 et 50 ans. On appelle \(1/32\) année\(^{-1}\) le taux de vieillissement de la population (\(32=50-18\)). Supposons que cette population soit divisée en dix-huit groupes, avec neuf groupes d'hommes (figure 1) et neuf groupes de femmes (figure 2).
Les travailleuses du sexe et les clients sont à risque s'ils n'utilisent pas toujours des préservatifs, et en sécurié s'ils utilisent toujours des préservatifs. De même, les drogués sont à risque s'ils réutilisent parfois des seringues, et en sécurité s'ils ne font jamais cela.

Considérons le diagrammes pour les hommes (figure 1). On définit
On suppose aussi que les drogués continuent à s'injecter de la drogue toute leur vie et qu'ils restent à risque ou sûrs. Cette simplification néglige l'impact des centres de désintoxication volontaires, des centres de réhabilitation obligatoires, des centres de rééducation par le travail et des programmes pilotes de réduction des risques pour la période de temps où l'on utilise le modèle dans le paragraphe 6, c'est-à-dire de 1994 à 2004. En effet, un tel centre de réhabilitation a été créé à Kunming en 1989, mais une enquête a montré que 80% des drogués qui y sont passés récidivaient avant deux années [31]. Avec des résultats légèrement meilleurs, un centre pilote de désintoxication volontaire, qui a sept cliniques dans Kunming [39], a offert un traitement à base de méthadone depuis 1996 pour les drogués qui pouvaient se le payer mais avec un taux de récidive de 70% [15]. Ces taux élevés, qui justifient d'une certaine manière notre modèle simplifié, sont peut-être dûs à la proximité des zones de production de l'héroïne, notamment le Myanmar qui amène de l'héroïne particulièrement pure à Kunming. Ceci cause une addiction plus forte et plus durable [31].
Considérons maintenant le diagramme pour les femmes (figure 2). On définit
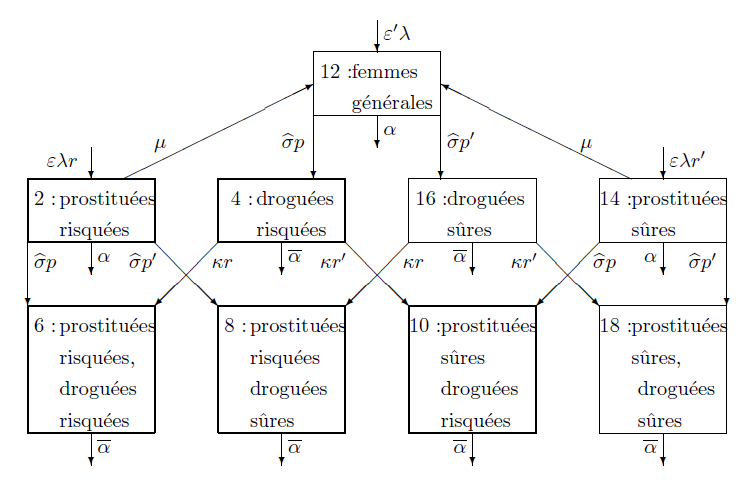
Ce modèle ne tient pas compte de la transmission du VIH par la collecte non sécurisée de sang, par les relations sexuelles non commerciales, par la mère à l'enfant et par les homosexuels. Il est centré autour du point où le VIH commence à se propager des utilisateurs de drogue aux travailleuses du sexe et à leurs clients à cause de l'existence des groupes 5 et 6 : drogués à risque qui sont aussi des clients à risque, travailleuses du sexe qui sont à risque. Les composantes du vecteur \(\,\Lambda(t)\) et de la matrice \(\mathbb{A}(t)\) qui sont non nulles se déduisent des figures 1 et 2. Par exemple, \(\Lambda_2=\varepsilon\, \lambda\, r\), \(\mathbb{A}_{1,1}=\alpha+\sigma\) et \(\mathbb{A}_{1,11}=-\tau\, q\).
Tournons-nous vers la forme des contacts:
Enfin, dans le cas où \(\gamma(t,x)\,\) ne dépend pas de t (c'est-à-dire avant l'introduction des traitements antirétroviraux), alors il y a une loi de probabilité fixe \(\,T_I\,\) pour la période d'incubation du SIDA. \(\exp(-\int_0^x \gamma(t)\, dt)\,\) est la probabilité qu'une personne infectée par le VIH n'ait pas le SIDA après x années d'infection. On a \[1-\int_0^x T_I(t)\, dt= \exp \left (-\int_0^x \gamma(t)\, dt \right ).\] Ainsi, avec une formule pour \(\,T_I(x)\), \(\,\gamma(x)\,\) se calcule avec la formule \[\gamma(x)=T_I(x)/\left (1-\int_0^x T_I(t)\, dt \right ).\]
Dans cette section, on discute du seuil épidémique pour le modèle avec 18 groupes et des paramètres indépendants du temps et l'on calcule la matrice de prochaine génération Ω donnée par (5). Noter que les groupes 1 à 10 sont des groupes essentiels, qu'ils sont reliés, que les groupes 12 et 16 sont à la fois des sources et des puits, que les groupes 11, 13, 14 et 15 sont des sources et que le groupe 18 est un puits. Le groupe 17 n'est ni un groupe essentiel, ni une source, ni un puits. On voit tout d'abord que l'état d'équilibre sans maladie pour la population masculine est donné par \begin{eqnarray*} S_{11}^0&=&\frac{\lambda}{\alpha+\sigma+\tau}\, , \quad S_1^0=\frac{\tau\, q}{\alpha+\sigma}\, S_{11}^0\, ,\quad S_{13}^0= \frac{\tau\, q'}{\alpha+\sigma}\, S_{11}^0\, ,\\ S_3^0&=&\frac{\sigma\, p}{\overline{\alpha}+\tau}\, S_{11}^0\, ,\quad S_{15}^0=\frac{\sigma\, p'}{\overline{\alpha}+\tau}\, S_{11}^0\, ,\\ S_5^0&=&\frac{\sigma\, p\, \tau\, q}{\overline{\alpha}} \Bigl (\frac{1}{\alpha+\sigma} + \frac{1}{\overline{\alpha}+\tau}\Bigr ) S_{11}^0\, ,\quad S_7^0=\frac{\sigma\, p'\, \tau\, q}{\overline{\alpha}} \Bigl (\frac{1}{\alpha+\sigma} + \frac{1}{\overline{\alpha}+\tau}\Bigr ) S_{11}^0\, ,\\ S_9^0&=&\frac{\sigma\, p\, \tau\, q'}{\overline{\alpha}} \Bigl (\frac{1}{\alpha+\sigma} + \frac{1}{\overline{\alpha}+\tau}\Bigr ) S_{11}^0\, ,\quad S_{17}^0=\frac{\sigma\, p'\, \tau\, q'}{\overline{\alpha}} \Bigl (\frac{1}{\alpha+\sigma} + \frac{1}{\overline{\alpha}+\tau}\Bigr ) S_{11}^0\, . \end{eqnarray*} Pour la population féminine, l'état d'équilibre sans maladie est donné par \begin{eqnarray*} S_2^0&=&\frac{\varepsilon\, \lambda\, r}{\alpha+\widehat{\sigma}+\mu}\, ,\quad S_{14}^0=\frac{\varepsilon\, \lambda\, r'}{\alpha+\widehat{\sigma}+\mu}\, ,\quad S_{12}^0=\frac{\varepsilon'\, \lambda + \mu (S_2^0 + S_{14}^0)}{\alpha+\widehat{\sigma}}\\ S_4^0&=&\frac{\widehat{\sigma}\, p\, S_{12}^0}{\overline{\alpha}+\kappa}\, ,\quad S_{16}^0=\frac{\widehat{\sigma}\, p'\, S_{12}^0}{\overline{\alpha}+\kappa}\, ,\\ S_6^0&=&\frac{\widehat{\sigma}\, p\, S_2^0+\kappa\, r\, S_4^0}{\overline{\alpha}}\, ,\quad S_8^0=\frac{\widehat{\sigma}\, p'\, S_2^0 +\kappa\, r\, S_{16}^0}{\overline{\alpha}}\, ,\\ S_{10}^0&=&\frac{\widehat{\sigma}\, p\, S_{14}^0 + \kappa\, r'\, S_4^0}{\overline{\alpha}}\, ,\quad S_{18}^0=\frac{\widehat{\sigma}\, p'\, S_{14}^0+\kappa\, r'\, S_{16}^0}{\overline{\alpha}}\, . \end{eqnarray*} Les seuls coefficients non nuls de la matrice \(\mathbb{B}^{\mathrm{drogue}}(N)\) sont \[ \mathbb{B}^{\mathrm{drogue}}_{i,j}(N)= \frac{B\, \pi}{N_{\mathrm{drogu\acute{e}s\,\grave{a}\,risque}}} \quad i,j=3,4,5,6,9,10, \] avec \(N_{\mathrm{drogu\acute{e}s\,\grave{a}\,risque}}=N_3+N_4+N_5+N_6+N_9+N_{10}\). On définit \[\beta_0=\int_0^\infty e^{-\alpha\, t - \int_0^t \gamma(x)\, dx}\, dt\, ,\] avec des expressions similaires pour \(\beta_\sigma\), \(\beta_{\hat{\sigma}}\), \(\beta_{\sigma+\tau}\) et \(\beta_{\hat{\sigma}+\mu}\). On remplace α par α+σ, \(\,\alpha+\widehat{\sigma}\), α+σ+τ et \(\alpha+\widehat{\sigma}+\mu\). On définit de même \(\overline{\beta}_0\), \(\overline{\beta}_\tau\) et \(\overline{\beta}_\kappa\,\), avec \(\overline{\alpha}\) qui remplace \(\alpha\). On obient pour la matrice de la proposition 5 : \begin{equation}\tag{12} \frac{\Omega^{\mathrm{drogue}}_{i,j}\, S^0_{\mathrm{drogu\acute{e}\, \grave{a}\,risque}}}{B\, \pi\, S_i^0}= \sum_{k=3,5,9} T_{k,j} + \sum_{k=4,6,10} T_{k,j} \end{equation} avec \(i=3,4,5,6,9,10\) et \(j=1\ldots 18\,\), alors que \(\Omega^{\mathrm{drogue}}_{i,j}=0\,\) pour les autres indices. Rappelons que la définition de \(\,T_{i,j}\,\) se trouve juste après (6). Noter que le côté droit de (12) est l'espérance du temps qu'une personne séropositive passera infectée dans un groupe de drogués à risque, si elle appartenait au groupe j lors de son infection. En utilisant (6), on arrive à \[ \sum_{k=3,5,9} T_{k,j} + \sum_{k=4,6,10} T_{k,j}= \left\{\begin{array}{ll} \overline{\beta}_0 &j=3,4,5,6,9,10,\\ p\,\sigma\, \frac{\overline{\beta}_0-\beta_\sigma}{\alpha+\sigma-\overline{\alpha}} \, &j=1,11,13,\\ p\,\widehat{\sigma}\, \frac{\overline{\beta}_0-\beta_{\hat{\sigma}}}{\alpha+\hat{\sigma}-\overline{\alpha}} \, & j=2,12,14,\\ \end{array} \right. \] et 0 pour \(j=7,8,15,16,17,18\). \(\Omega^{\mathrm{drogue}}\,\) a un rayon spectral \[R_0^{\mathrm{drogue}}= B\, \pi\, \overline{\beta}_0.\] En effet, écrivons l'équation caractéristique pour les valeurs propres de \(\,\Omega^{\mathrm{drogue}}\,\) comme un déterminant et développons le déterminant selon les lignes pleines de zéros. Le problème se réduit à trouver les valeurs propres d'une matrice de rang 1 de la forme \[(S_3\,S_4\,S_5\,S_6\,S_9\,S_{10})^T\,(1\,1\,1\,1\,1\,1)\,B\, \pi\,\overline{\beta}_0 / S^0_{\mathrm{drogu\acute{e}s\,\grave{a}\,risque}}.\] \(^T\,\) désigne la transposition des vecteurs. Mais le rayon spectral des matrices de la forme \[(y_1\,\ldots\,y_k)^T (z_1\,\ldots\,z_k)\] est donné par \[\sum_{i=1}^k y_i\, z_i,\] comme on le vérifie facilement, sinon voir [17, p. 80].
Les seuls coefficients non nuls de la matrice \(\mathbb{B}^{\mathrm{sexe}}(N)\) sont \[ \mathbb{B}^{\mathrm{sexe}}_{i,j}(N)=\left \{\begin{array}{lll} \frac{A\, \pi_2}{N_{\mathrm{prostitu\acute{e}es}}} &\quad &i=1,5,7;\,j=2,6,8,\\ \frac{A\, \pi_1}{N_{\mathrm{prostitu\acute{e}es}}}&\quad & i=2,6,8;\,j=1,5,7, \end{array} \right.\] avec \(\,N_{\mathrm{prostitu\acute{e}es}}=N_2+N_6+N_8+N_{10}+N_{14}+N_{18}\). On obtient pour la matrice \(\,\Omega^{\mathrm{sexe}}\) \[ \frac{\Omega^{\mathrm{sexe}}_{i,j} \, S^0_{\mathrm{prostitu\acute{e}es}}}{A\, S_i^0} = \left\{\begin{array}{lll} \pi_2 \sum_{k=2,6,8} T_{k,j},& &i=1,5,7,\,j=2j'\, ,\\ \pi_1 \sum_{k=1,5,7} T_{k,j},& &i=2,6,8,\,j=2j'+1\, ,\\ \end{array} \right. \] et \(\Omega^{\mathrm{sexe}}_{i,j}=0\,\) sinon. Noter que \(\,\sum_{k=2,6,8} T_{k,j}\) (resp. \(\sum_{k=1,5,7} T_{k,j}\)) est l'espérance du temps qu'une personne séropositive passera infectée dans un groupe de travailleuses du sexe à risque (resp. de clients à risque), si elle appartenait au groupe j lors de son infection. En utilisant (6), on arrive à \begin{eqnarray*} \sum_{i=2,6,8} T_{i,12} &=&\frac{\kappa\, r\, \widehat{\sigma}}{\alpha+\widehat{\sigma}-\overline{\alpha}-\kappa} \Biggl [\frac{\overline{\beta}_0-\overline{\beta}_\kappa}{\kappa} - \frac{\overline{\beta}_0-\beta_{\hat{\sigma}}}{\alpha+\widehat{\sigma}-\overline{\alpha}} \Biggr ]\\ \sum_{i=2,6,8} T_{i,14} &=& \sum_{i=2,6,8} T_{i,12} - \frac{\kappa\, r\, \widehat{\sigma}}{\alpha+\widehat{\sigma}+\mu-\overline{\alpha}-\kappa} \Biggl [\frac{\overline{\beta}_0-\overline{\beta}_\kappa}{\kappa} - \frac{\overline{\beta}_0-\beta_{\hat{\sigma}+\mu}}{\alpha+\widehat{\sigma}+\mu-\overline{\alpha}} \Biggr ]\\ \sum_{i=2,6,8} T_{i,2} &=& \sum_{i=2,6,8} T_{i,14} + \beta_{\hat{\sigma}+\mu}+\widehat{\sigma}\, \frac{\overline{\beta}_0-\beta_{\hat{\sigma}+\mu}}{\alpha+\hat{\sigma}+\mu-\overline{\alpha}}\, ,\\ \sum_{i=2,6,8} T_{i,4} &=& \sum_{i=2,6,8} T_{i,16} =r (\overline{\beta}_0 - \overline{\beta}_\kappa)\, , \\ \sum_{i=2,6,8} T_{i,6} &=&\sum_{i=2,6,8} T_{i,8} = \sum_{i=1,5,7} T_{i,5} = \sum_{i=1,5,7} T_{i,7} =\overline{\beta}_0\, ,\\ \sum_{i=1,5,7} T_{i,1}&=&\beta_\sigma + \sigma\, \frac{\overline{\beta}_0-\beta_\sigma}{\alpha+\sigma-\overline{\alpha}}\, ,\\ \sum_{i=1,5,7} T_{i,3}&=& \sum_{i=1,5,7} T_{i,15} = q (\overline{\beta}_0-\overline{\beta}_\tau)\, ,\\ \sum_{i=1,5,7} T_{i,11}&=& \sigma\, q \Biggl [ \frac{\overline{\beta}_0 - \beta_\sigma }{\alpha+\sigma-\overline{\alpha}} - \frac{\overline{\beta}_0 - \beta_{\sigma+\tau} }{\alpha+\sigma+\tau-\overline{\alpha}} \Biggr ] \\ &&\quad + \frac{\tau\, q\, \sigma}{\alpha+\sigma-\overline{\alpha}} \Biggl [ \frac{\overline{\beta}_0 - \overline{\beta}_\tau}{\tau} - \frac{\overline{\beta}_0 - \beta_{\sigma+\tau} }{\alpha+\sigma+\tau-\overline{\alpha}} \Biggr ]\, ,\\ \sum_{i=1,5,7} T_{i,9}&=& \sum_{i=1,5,7} T_{i,13} = \sum_{i=1,5,7} T_{i,17} = \sum_{i=2,6,8} T_{i,10} = \sum_{i=2,6,8} T_{i,18} = 0\, . \end{eqnarray*}
\(\Omega^{\mathrm{sexe}}\,\) a un rayon spectral \begin{equation} R_0^{\mathrm{sexe}}=\frac{A}{S^0_{\mathrm{prostitu\acute{e}es}}} \Biggl \{\pi_1\, \pi_2 \Biggl [ \sum_{j=1,5,7} \Biggl (\sum_{i=1,5,7} T_{i,j} \Biggr ) S_j^0 \Biggr ]\\ \Biggl [\sum_{j=2,6,8} \Biggl (\sum_{i=2,6,8} T_{i,j} \Biggr ) S_j^0 \Biggr ] \Biggr \}^{1/2}. \end{equation} En effet, on écrit comme un déterminant l'équation caractéristique pour les valeurs propres de \(\Omega^{\mathrm{sexe}}\). On développe le déterminant le long des lignes pleines de zéros. On prend les lignes dans l'ordre 1-5-7-2-6-8. Le problème revient à trouver les valeurs propres d'une matrice de rang 2 de la forme \[ M=\left(\begin{array}{c|c}0 & M_2\\ \hline M_1 & 0\end{array}\right ) . \] \(M_1\) et \(M_2\) sont des matrices \(3\times 3\) données par \begin{eqnarray*} M_1&=& \pi_1\,\mathrm{colonne}(S_i)_{i=2,6,8}\,\mathrm{ligne}\Biggl (\sum_{i=1,5,7} T_{i,j}\Biggr )_{j=1,5,7},\\ M_2&=& \pi_2\,\mathrm{colonne}(S_i)_{i=1,5,7}\,\mathrm{ligne}\Biggl (\sum_{i=2,6,8} T_{i,j}\Biggr )_{j=2,6,8}. \end{eqnarray*} ξ est une valeur propre non nulle de M si et seulement si \(\,\xi^2\) est une valeur propre non nulle de la matrice \(M_1\, M_2\). Le rayon spectral se calcule comme ci-dessus puisque c'est une matrice de rang un. Voir par exemple [42, p. 415].
Considérons le cas où la loi de probabilité de l'incubation du SIDA est une loi Gamma \[T_I(x)=\omega^\nu x^{\nu-1}\, e^{-\omega\, x} / \Gamma(\nu).\] ω et ν sont liés à la moyenne \(M_I\) et à la variance \(V_I\) de \(T_I\) par les relations \(\omega=M_I/V_I\) et \(\nu=(M_I)^2/V_I\). En intégrant par parties, on obtient \[\beta_0=\int_0^\infty e^{-\alpha x}\, \Bigl (1-\int_0^x T_I(t)\, dt\Bigr )\, dx =\frac{1}{\alpha} \Bigl (1-\int_0^\infty e^{-\alpha x}\, T_I(x)\, dx \Bigr ) =\frac{1- (1+\alpha/\omega)^{-\nu}}{\alpha}\] et des expressions similaires pour \(\beta_\sigma\), \(\beta_{\hat{\sigma}}\), \(\beta_{\hat{\sigma}+\mu}\), \(\beta_{\sigma+\tau}\), \(\overline{\beta}_0\), \(\overline{\beta}_\tau\) et \(\overline{\beta}_\kappa\).
Il semble difficile de calculer explicitement le rayon spectral de la matrice complète Ω. On peut bien sûr calculer ce rayon spectral numériquement pour toutes valeurs des paramètres avec les formules précédentes. On rappelle que \(R_0 \geq \max \{R_0^{\mathrm{sexe}},\, R_0^{\mathrm{drogue}}\}\). Cette section donne des formules explicites pour \(\,R_0^{\mathrm{sexe}}\) et \(R_0^{\mathrm{drogue}}\).
Pour la simulation, on a pris les valeurs des paramètres du tableau 3.
| période | 1994-2004 | |
| \(\alpha\) | taux de vieillissement | 1/32 an\(^{-1}\) |
| \(\overline{\alpha}\) | taux de sortie des drogués | 1/18 an\(^{-1}\) | \(1/\delta\) | espérance de vie avec le SIDA | 1 an |
| \(M_I\) | durée moyenne de l'incubation | 12,6 ans |
| \(\sqrt{V_I}\) | écart type de la période d'incubation | 9,4 ans |
| \(\lambda\) | flux d'entrée | 27 000 an\(^{-1}\) |
| \(\sigma\) | taux masculin de démarrage de la drogue | \(9\times 10^{-4}\) an\(^{-1}\) |
| \(\widehat{\sigma}\) | taux féminin de démarrage de la drogue | \(3\times 10^{-4}\) an\(^{-1}\) |
| \(\tau\) | taux pour devenir client | \(\mbox{1,2}\times 10^{-2}\) an\(^{-1}\) |
| \(A\) | visites des clients | 2,4 mois\(^{-1}\) |
| \(1/\mu\) | durée du travail | 2,5 ans |
| \(\varepsilon\) | jeunes femmes devenant travailleuses du sexe | 30% |
| p | nouveaux drogués à risque | 25% \(\nearrow\) 50% |
| q | nouveaux clients à risque | 70% \(\searrow\) 10% |
| r | nouvelles travailleuses du sexe à risque | 70% \(\searrow\) 10% |
| \(\pi_1\) | probabilité de transmission de l'homme à la femme | 0,7% |
| \(\pi_2\) | probabilité de transmission de la femme à l'homme | 1,4% |
| \(B\, \pi\) | taux d'échange de seringues \(\times\) probabilité de transmission | 4 an\(^{-1}\) |
| \(\kappa\) | femmes droguées se prostituant | 0,1 an\(^{-1}\) |
Quelques commentaires sont nécessaires:
 |
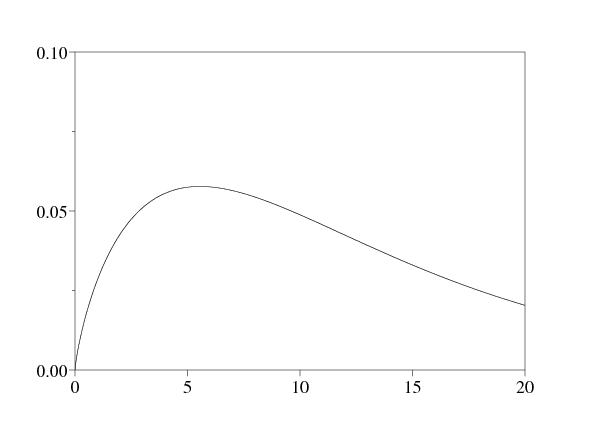 |
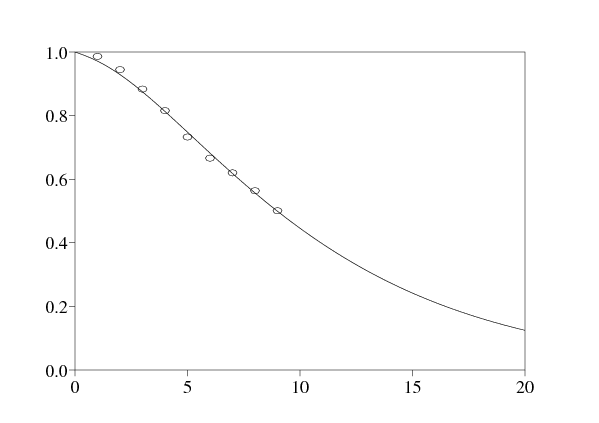
La figure 4 est le résultat de la simulation du modèle avec les valeurs des paramètres comme ci-dessus; elle montre le nombre total de personnes séropositives et le nombre total de personnes vivant avec le SIDA.
De nombreux cas ne sont pas identifiés car les personnes craignent les discriminations en cas de test du VIH positif; il est donc difficile d'avoir des estimations du nombre total de cas à Kunming. On sait qu'en septembre 2003, 13948 cas de VIH et 841 cas de SIDA avaient été rapportés au Yunnan [1] et qu'en septembre 2004, ces nombres avaient atteint 17390 et 1118 [2]. Les estimations pour le nombre total de cas de VIH en 2004 tournent autour de 100000 pour toute la province [1].
La présente simulation donne environ 4200 personnes avec le VIH ou le SIDA à la fin 2004 dans la ville de Kunming parmi les personnes âgées de 18 à 50 ans, ce qui inclut la grande majorité des infections. Étant donné que la population du Yunnan est d'environ 43 millions en 2004 (42,88 millions au recensement de l'an 2000), la prévalence calculée pour toute la population de Kunming (\(4\,200/2\,290\,000 \simeq \mbox{0,18}\%\)) est proche de celle estimée pour tout le Yunnan (\(100\,000/43\,000\,000 \simeq \mbox{0,23}\%\)). Les zones proches de la frontière du Myanmar ont plus d'infections, tandis que les zones rurales isolées en ont moins.
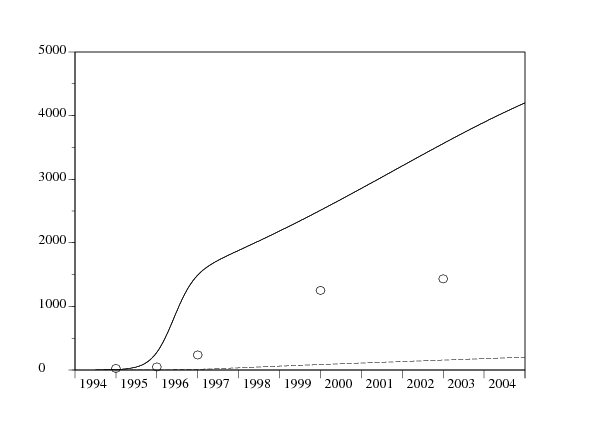
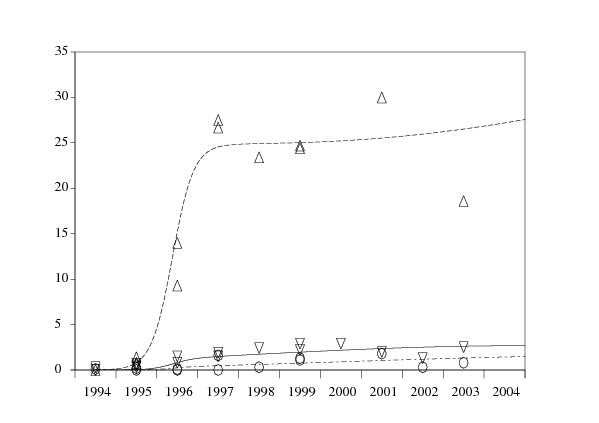
Comme la plupart des modèles épidémiques, les courbes sont assez sensibles aux variations des paramètres. Ce serait sûrement un problème si l'on voulait faire des prévisions pour le futur de l'épidémie, mais c'est plus un avantage lors de l'ajustement aux données. Une analyse de sensibilité des paramètres estimés est cependant difficile du fait que 19 paramètres interviennent dans le modèle (tableau 3).
Une autre raison de ne pas continuer la simulation pour faire des prédictions est que plusieurs mesures importantes ont été récemment adoptées à Kunming et au Yunnan, qui peuvent profondément changer la transmission:
Les nombres \(R_0\), \(R_0^{\mathrm{drogue}}\) et \(R_0^{\mathrm{sexe}}\,\) n'ont été définis que quand les paramètres du modèle sont constants. Mais p, q et r varient dans la simulation de la section précédente. Néanmoins, en utilisant les paramètres du tableau 3, on obtient que \(\,R_0^{\mathrm{drogue}}= B\, \pi\, \overline{\beta}_0 \simeq 32\). Ainsi le produit du taux d'échange des seringues B et de la probabilité de transmission par seringue π devrait être divisé par au moins 32 pour arrêter l'épidémie chez les utilisateurs de drogue. Des programmes d'échange des seringues peuvent réduire B, tandis qu'une campagne expliquant comment nettoyer les seringues peut réduire π. Ces mesures devraient atteindre \(1-1/32\simeq 97\%\,\) des utilisateurs de drogue. Un des buts fixés par le plan d'action pour l'arrêt, la prévention et le contrôle du VIH/SIDA (2001-2005) pour la fin 2005 était déjà que
« 95% de la population dans les centres de désintoxication, les centres de rééducation et les prisons aient une connaissance de base de la prévention du VIH ».Même si ce but était atteint dans ces institutions, certains utilisateurs de drogue ne passent pas par ces institutions. Donc atteindre 97% des personnes à risque semble assez difficile.
Avec les paramètres du tableau 3, on obtient aussi que \(R_0^{\mathrm{sexe}}\simeq \mbox{4,25} \sqrt{q\, r}\). On a ainsi \(\,R_0^{\mathrm{sexe}} < 1\) dès que la moyenne géométrique des comportements à risque chez les clients et les travailleuses du sexe est telle que \(\sqrt{q\, r} < 23\%\). Rappelons qu'en 2001, 46% des clients et 35% des travailleuses du sexe étaient à risque, donc \(\,\sqrt{\mbox{0,46}\times \mbox{0,35}}\simeq40\%\). Ainsi, il suffirait de diviser les comportements à risque par deux pour arrêter l'épidémie sexuelle.
Le raisonnement ci-dessus considère les deux voies de transmission séparément. On peut se demander si c'est correct puisque le modèle couple les deux voies. Choisissons par exemple q=r et faisons varier B. On obtient la figure 6, qui montre les lignes de niveau de \(\,R_0\,\) calculées avec les formules de la Section 5. Au lieu de mettre q=r et B sur les axes, on a mis \(R_0^{\mathrm{sexe}}\) et \(R_0^{\mathrm{drogue}}\) qui leur sont proportionnels.
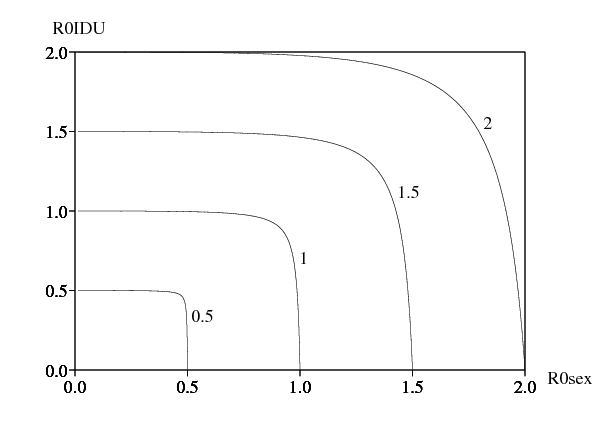
Ce qui est remarquable, c'est que l'approximation \(R_0 \simeq \max \bigl \{R_0^{\mathrm{sexe}},R_0^{\mathrm{drogue}} \bigr \}\) semble assez bonne, au moins près du seuil \(R_0=1\). Ceci justifie d'une certaine manière le fait de considérer les deux voies de transmission séparément dans la discussion du seuil épidémique.
On a \(\,R_0 ^{\mathrm{sexe}}\ll R_0^{\mathrm{drogue}}\). Parmi les mesures nouvelles adoptées à Kunming et au Yunnan, celles visant les utilisateurs de drogue sont plus urgentes que celles visant la transmission sexuelle. Cependant le groupe impliqué dans la transmission sexuelle (les travailleuses du sexe et leurs clients) est bien plus grand que le groupe impliqué dans la transmission par injection de drogue. De plus le modèle ne prend pas en compte la transmission sexuelle non commerciale, qui peut impliquer un groupe encore plus grand mais qui peut être réduite si par exemple les clients et les (anciennes) travailleuses du sexe utilisent aussi des préservatifs pour leurs relations non commerciales. Une discussion précise de l'efficacité des différentes formes de prévention requiert plus d'information sur les coûts. Cela sort du cadre du présent article, mais on espère pouvoir y travailler à l'avenir.
Des parties de cet article ont été rédigées pendant que N. Bacaër visitait le Laboratoire d'Informatique, Automatique et Mathématiques Appliquées (LIAMA) à Pékin, et pendant que X. Abdurahman visitait l'Institut de Recherche pour le Développement à Bondy en France.