J. Math. Biol. 53 (2006) p. 421-436
Nicolas Bacaër
Institut de recherche pour le développement,
Bondy, France
nicolas.bacaer@ird.fr
Laboratoire d'écologie animale terrestre, Faculté des sciences Semlalia, Marrakech, Maroc
La leishmaniose cutanée est une maladie à vecteurs transmise aux humains par des phlébotomes. On développe dans cet article un modèle mathématique qui tient compte de la saisonnalité de la population de vecteurs et de la distribution de la période de latence entre l'infection et les symptômes chez les humains. On ajuste les paramètres à des données de la province de Chichaoua au Maroc. On propose aussi une généralisation de la définition de la reproductivité aux environnements périodiques. Pour l'épidémie à Chichaoua, on estime que \(R_0\simeq \mbox{1,94}\). L'épidémie s'arrêterait si la population de vecteurs était divisée par le carré de ce nombre : \((R_0)^2\simeq \mbox{3,76}\).
La leishmaniose est un complexe de maladies vectorielles causées par des protozoaires du genre Leishmania. Le parasite est transmis aux humains par des piqûres de phlébotomes femelles (Diptera: Psychodidae: Phlebotominae). La maladie est endémique dans de nombreuses régions d'Afrique, d'Amérique du Sud, d'Amérique centrale, du sud de l'Europe, d'Asie et du Moyen-Orient. La leishmaniose comprend quatre entités principales d'un point de vue éco-épidémiologique: leishmaniose viscérale zoonotique ou anthroponotique, et leishmaniose cutanée zoonotique ou anthroponotique. Dans les formes anthroponotiques, les humains sont la seule source d'infection pour les phlébotomes vecteurs. Dans les cycles de transmission zoonotiques, les animaux sont des réservoirs qui maintiennent et propagent les parasites. Il y a chaque année environ 500000 nouveaux cas humains de leishmaniose viscérale et de 1 à 1,5 million de cas de leishmaniose cutanée dans le monde (Desjeux, 2004). La leishmaniose viscérale est fatale si elle n'est pas traitée. La leishmaniose cutanée guérit en général toute seule mais peut laisser des cicatrices défigurantes.
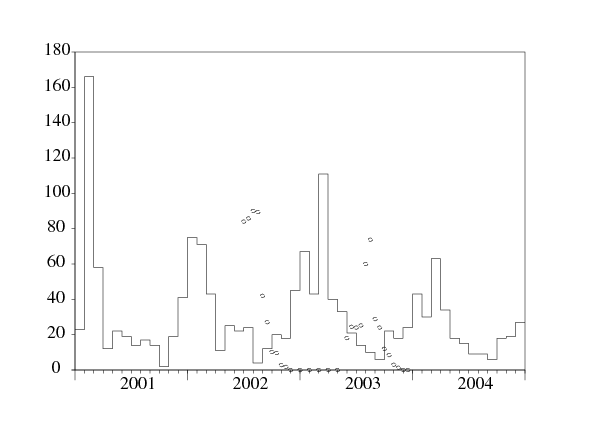
D'après le Ministère marocain de la santé publique (2001), la leishmaniose cutanée anthroponotique due à Leishmania tropica est une maladie émergente dans la province de Chichaoua: entre le début de l'année 2000 et la fin de l'année 2004, 1877 cas ont été rapportés officiellement. La figure 1 montre l'évolution mensuelle du nombre de cas rapportés dans la ville d'Imintanoute, qui représente environ 80% des cas de la province, entre le début de l'année 2001 et la fin de l'année 2004. Quelques cas (43 au total) ont déjà été observés pendant l'année 2000, mais le rapport mensuel détaillé n'est pas disponible.

Une étude sur le terrain (Guernaoui et coll., 2005) a montré que les phlébotomes de l'espèce Phlebotomus sergenti sont responsables de la transmission et que la transmission est anthroponotique. Aucun réservoir animal tel que des chiens n'a été détecté pour cette épidémie particulière. La figure 1 montre aussi des estimations de la population de Phlebotomus sergenti obtenues avec des pièges une ou deux fois par mois de juin 2002 à décembre 2003 (thèse de doctorat de S. Guernaoui). Noter que la population de vecteurs tombe à zéro entre décembre et mai. C'est dû au cycle de vie particulier des phlébotomes dans cette région: pendant ces mois, seuls les œufs et les larves survivent cachés dans le sol. Quand la température augmente au début de chaque été, les larves se métamorphosent en adultes qui volent. La métamorphose s'arrête quand la saison froide réapparaît.
L'objectif de ce travail est de développer un modèle mathématique de cette épidémie, d'estimer certains paramètres du cycle de transmission et d'estimer la reproductivité, qui mesure l'effort nécessaire pour arrêter l'épidémie. Il est intéressant de constater que cette étude particulière nous a conduit à une nouvelle définition générale de la reproductivité dans un environnement périodique.
(Bensalah et coll., 1994 ; Burattini et coll., 1998 ; Chaves et Hernandez, 2004 ; Hasibeder et coll., 1992 ; Kerr et coll., 1997 ; Rabinovich et Feliciangeli, 2004) ont déjà développé divers modèles mathématiques pour la leishmaniose. Seul (Bensalah et coll., 1994) simule une population fluctuante de vecteurs mais sans analyse mathématique et sans données de terrain.
Pour notre modèle, on insiste sur deux points. Premièrement, il y a des fluctuations saisonnières très marquées de la population de vecteurs. On obtient les modèles les plus simples en supposant que la population de vecteurs est périodique avec une période égale à un an. Deuxièmement, il y a un retard de plusieurs mois entre l'infection, qui a lieu en été ou en automne lorsque la population de vecteurs est non nulle, et l'apparition de cas symptomatiques, qui est au plus haut en hiver et au printemps. Voir la figure 1.
Les plus anciens modèles mathématiques pour des maladies à vecteurs remontent à Ronald Ross (1911), qui étudiait le paludisme. Notre modèle est en quelque sorte une extension de son second modèle (Lotka, 1923). La population de vecteurs est partagée entre vecteurs sains et vecteurs infectés. Les humains sont partagés entre sains, infectés et immunisés.
De plus, on suppose que la population de vecteurs fluctue de manière périodique. (Anderson et May, 1991, p. 404) a étudié numériquement l'influence de la saisonnalité sur les maladies à vecteurs. (Heesterbeek et Roberts, 1995a et 1995b) et (Diekmann et Heesterbeek, 2000, p. 148) donnent des résultats mathématiques en relation avec la théorie de Floquet pour les équations différentielles périodiques. Dans (Heesterbeek et Roberts, 1995b, §2.3), la définition du seuil épidémique censée remplacer la reproductivité, lorsque la population de vecteurs est périodique, est un peu étrange. Dans le cas particulier où la population de vecteurs est constante, la définition est le rayon spectral d'une matrice semblable (au sens de la théorie des matrices) mais non égale à la matrice de prochaine génération.
Par ailleurs, ces travaux ne contiennent pas de retard entre l'infection et les symptômes chez les humains autre qu'un retard distribué exponentiellement. On voit sur la figure 1 qu'un retard fixe donnerait un mauvais ajustement aux données pour l'épidémie de leishmaniose cutanée à Imintanoute. La population de vecteurs est non nulle pendant six mois de l'année. Mais les cas humains se rencontrent tout au long de l'année. Un retard distribué est nécessaire. Les premiers modèles en épidémiologie avec un retard distribué remontent à Kermack et McKendrick (1927) et font intervenir des équations aux dérivées partielles. Peu de travaux combinent ces retards distribués avec une influence périodique dans le contexte de l'épidémiologie. C'est le cas de (Williams et Dye, 1997). Mais la discussion porte principalement sur les distributions exponentielles. Cependant plusieurs travaux discutent de distributions générales dans d'autres domaines de la dynamique des populations:
En résumé, du point de vue général de la dynamique des populations, notre contribution est de rendre plus explicite la définition du seuil épidémique pour les maladies à vecteurs avec une population périodique de vecteurs. La définition semble nouvelle même dans le cas où la période d'incubation est distribuée exponentiellement de sorte que le modèle se réduit à un système d'équations différentielles ordinaires. De plus on donne un algorithme pour le calcul de la reproductivité dans le cas général. Du point de vue de l'épidémiologie, notre contribution est d'estimer certains paramètres dans la transmission de la leishmaniose cutanée lors d'une épidémie au Maroc. On estime le temps entre l'infection et les symptômes par une distribution Gamma avec une moyenne de 6 mois et un écart type de 1,5 mois. On a \(R_0\simeq \mbox{1,94}\). Le modèle suggère que l'épidémie s'arrêterait si la population de vecteurs était divisée par le carré de ce nombre : \((R_0)^2\simeq \mbox{3,76}\).
Le plan de l'article est le suivant. La section 2 présente le système d'équations différentielles utilisé pour modéliser l'épidémie. La section 3 analyse le modèle, en particulier la stabilité de la situation sans infection. La section 4 présente une simulation avec des paramètres ajustés aux données épidémiques de la ville d'Imintanoute. On estime ensuite le seuil épidémique pour cette épidémie particulière. La section 5 introduit une définition générale de la reproductivité dans un environnement périodique et discute de son lien avec des travaux antérieurs.
On définit
On suppose que \(\Lambda(t)\) est une fonction périodique de période \(T\). Alors le système (1)-(2) a une solution périodique sans maladie donnée par \(s(t)=p(t)\), \(i(t)=0\), \(S(t)=P\) et \(I(t)=R(t)=0\). \(p(t)\) est l'unique solution périodique de \(p'(t)=\Lambda(t)-\mu\, p(t)\). La stabilité s'étudie en linéarisant le système. On a \begin{eqnarray} &&\tilde{i}'(t) =\beta\, \widehat{\pi}\, p(t)\, \frac{\tilde{I}(t)}{P} -\mu\, \tilde{i}(t)\, ,\\ &&\tilde{I}(t,0)=\beta\, \pi\, \tilde{i}(t)\, ,\quad \frac{\partial \tilde{I}}{\partial t}(t,\tau)+\frac{\partial \tilde{I}}{\partial \tau}(t,\tau)=-\alpha(\tau)\, \tilde{I}(t,\tau)\, , \end{eqnarray} avec la condition initiale \(\tilde{i}(0,\tau)=\tilde{i}_0(\tau)\) et \(\tilde{I}(0,\tau)=\tilde{I}_0(\tau)\). Ce système comprend à la fois une équation différentielle ordinaire linéaire et une équation aux dérivées partielles linéaire. Pour que la discussion soit plus symétrique, on définit
\(\mathcal{E}\) est l'ensemble des fonctions continues périodiques de période T à valeurs dans \(\mathbb{R}^2\). Muni de la norme du supremum, c'est un espace de Banach. Thieme (1984) a étudié le comportement asymptotique des équations telles que (4): \(u(t) \sim e^{\lambda^* t}\, v(t)\). \( \,\lambda^* \) est un nombre réel et \(v \in \mathcal{E}\) est une fonction positive, non identiquement nulle et telle que \begin{equation}\tag{5} v(t)=\int_0^\infty e^{-\lambda^* \tau} A(t,\tau)\, v(t-\tau)\, d \tau.\end{equation} Plus précisément, il existe un unique nombre réel \(\lambda^*\) pour lequel on puisse trouver \(v \in \mathcal{E}\) qui soit positif et non identiquement nul (Thieme, 1984 ; Jagers et Nerman, 1985).
Définissons \(R_0\) comme le rayon spectral de l'opérateur linéaire qui à \(w \in \mathcal{E}\) associe la fonction \(t\mapsto \int_0^\infty A(t,\tau)\, w(t-\tau)\, d \tau\), aussi dans \(\mathcal{E}\). Cet opérateur linéaire est positif. \(R_0\) se caractérise par l'existence de \(w \in \mathcal{E}\) positif et non identiquement nul avec \begin{equation} \int_0^\infty A(t,\tau)\, w(t-\tau)\, d \tau = R_0 \, w(t).\tag{6} \end{equation} \(R_0\) a les propriétés d'un seuil épidémique: \(\lambda^* > 0\) si \(R_0 > 1\), tandis que \(\lambda^* < 0\) si \(R_0 < 1\).
En effet, pour tout nombre réel \(\lambda\), on définit \begin{eqnarray*} \mathcal{A}_\lambda : \mathcal{E} &\longrightarrow& \mathcal{E} \\ v &\longmapsto& \left (t \mapsto \int_0^\infty e^{-\lambda \tau} A(t,\tau)\, v(t-\tau)\, d \tau\right ). \end{eqnarray*} Le rayon spectral de \(\mathcal{A}_\lambda\) est noté \(R_\lambda\) . Noter que cette définition coïncide bien quand \(\lambda=0\) avec celle de \(R_0\). Pour tout λ, l'opérateur linéaire \(\mathcal{A}_\lambda\) est positif. De plus, \(\lambda_1 \leq \lambda_2\) implique que \(\mathcal{A}_{\lambda_1}\geq \mathcal{A}_{\lambda_2}\). Les propriétés du rayon spectral impliquent que \(\lambda \mapsto R_\lambda\) de \(\mathbb{R}\to \mathbb{R}\) est une fonction décroissante. Mais \(R_{\lambda^*}=1\) d'après l'équation (5). On a donc \(\lambda^* > 0\) si \(R_0 > 1\), et \(\lambda^* < 0\) si \(R_0 < 1\).
Si la fonction \(p(t)\) est une constante p, alors \(A(t,\tau)\) ne dépend pas de t. Dans ce cas, considérons la fonction constante \(w(t)\) égale à un vecteur propre positif de la matrice positive \(\int_0^\infty A(\tau)\, d\tau\). \(R_0\) est le rayon spectral de cette matrice, appelée matrice de prochaine génération (Diekmann et Heesterbeek, 2000, p. 74). Plus précisément, on obtient \begin{equation}\tag{7} R_0=\sqrt{\frac{\beta^2\, \pi\, \widehat{\pi}}{P} \times \frac{p}{\mu} \int_0^\infty g(\tau)\, d \tau}. \end{equation} On voit le produit du nombre moyen d'humains infectés par un phlébotome infecté \(\frac{\beta \pi}{\mu}\) avec le nombre moyen de phlébotomes infectés par un humain infecté \(\frac{\beta \widehat{\pi} p}{P} \int_0^\infty g(\tau)\, d\tau\).
Si la fonction \(p(t)\) n'est pas constante mais périodique, écrivons \(w=(w_1\, ,\, w_2)\). Alors (6) s'écrit \begin{eqnarray*} \frac{\beta\, \widehat{\pi}\, p(t)}{P} \int_0^\infty g(\tau)\, w_2(t-\tau)\, d \tau &=& R_0 \, w_1(t) \\ \beta\, \pi \int_0^\infty e^{-\mu \tau}\, w_1(t-\tau)\, d \tau &=& R_0 \, w_2(t). \end{eqnarray*} Insérons la seconde équation dans la première. Si le nombre \(r_0\) et une fonction positive, périodique de période T, non identiquement nulle \(w_1(t)\) sont solutions de \begin{equation}\tag{8} p(t) \int_0^\infty g(\tau) \int_0^\infty e^{-\mu \sigma} \, w_1(t-\tau-\sigma)\, d \sigma \, d \tau = r_0\, w_1(t), \end{equation} on a alors \begin{equation}\tag{9} R_0=\sqrt{\frac{\beta^2\, \pi\, \widehat{\pi}}{P}\times r_0}. \end{equation} La formule (9) géneralise la formule classique (7) pour les maladies à vecteurs avec une population de vecteurs saisonnière périodique. Noter que \(r_0\) est une fonction compliquée de \(p(t)\), \(g(x)\) et μ. Visiblement, \(r_0\) est une fonction décroissante de μ. Si la fonction \(p(t)\) est remplacé par \(\varepsilon\, p(t)\), alors \(r_0\) est remplacé par \(\varepsilon\, r_0\). Donc la conclusion classique selon laquelle une maladie à vecteurs peut être éradiquée si la population de vecteurs est divisée par le carré de la reproductivité, qui n'est valide a priori que pour une population constante de vecteurs, demeure vraie si la population de vecteurs est périodique.
Certains auteurs utilisent la notation \(R_0\) pour ce qui ici est \((R_0)^2\). (Heesterbeek et Roberts, 1995b, § 2.1) discute brièvement de ce point.
Estimons les paramètres du modèle. La population totale d'Imintanoute est d'environ 5000 habitants. Cependant certaines parties de la ville sont plus concernées que d'autres parce que les phlébotomes préfèrent les endroits où ils peuvent pondre leurs œufs, par exemple près de dépôts d'ordures. Il n'y a qu'un groupe homogène dans notre modèle. Une manière de traiter ce problème est de considérer que la population P, qui est initialement saine, est inconnue mais avec la contrainte P≤5000, et doit être déterminée lors de l'ajustement de la courbe épidémique aux données.
L'espérance de vie \(1/\mu\) d'un phlébotome adulte est, d'après les connaissances actuelles, d'environ 10 jours. On choisit donc \(\mu=3\) par mois.
Les données de la figure 1 montrent les fluctuations saisonnières de la population de vecteurs à une constante multiplicative près entre juin 2002 et décembre 2003. On prend comme base pour la population périodique de notre modèle les données entre janvier et décembre 2003. La population de vecteurs n'était pas strictement la même entre juin et décembre 2002 qu'entre juin et décembre 2003. La température mensuelle moyenne par exemple peut être un peu différente d'une année à l'autre. On définit
On supposons qu'au temps t=0, au début de l'année 2000, un humain importe l'infection dans la population saine. À cet instant, la population de vecteurs est nulle. La condition initiale est: \(s(0)=0\), \(i(0)=0\), \(S(0)=P-1\), \(I(0,\tau)=\delta_{\tau=0}\) (masse de Dirac à \(\tau=0\)) et \(R(0)=0\).
On suppose que la distribution de probabilité \(f(\tau)\) du temps écoulé entre l'infection et les symptômes chez les humains est une distribution Gamma: \begin{equation} f(\tau)=a^\nu\, \tau^{\nu-1}\, e^{-a\, \tau} / \Gamma(\nu). \end{equation} Pour les calculs numériques, noter que \[\alpha(\tau)=\frac{f(\tau)}{1-\int_0^\tau f(\sigma)\, d \sigma} \simeq -\frac{f'(\tau)}{f(\tau)} = a - \frac{\nu-1}{\tau},\quad \tau \to +\infty.\]
Considérons le système (1)-(2). Divisons les deux premières équations par \(p_{\max}\). On a \begin{eqnarray} &&\bar{s}'(t)=\bar{\Lambda}(t) - \mu\, \bar{s}(t) - \beta\, \widehat{\pi}\, \bar{s}(t)\, \frac{I(t)}{P}\, ,\quad \bar{i}'(t)=\beta\, \widehat{\pi}\, \bar{s}(t)\, \frac{I(t)}{P} - \mu\, \bar{i}(t)\, ,\tag{11}\\ &&S'(t)=-\beta\, \pi\, p_{\max} \, \bar{i}(t)\, \frac{S(t)}{P} + \gamma\, R(t)\, ,\\ &&I(t,0)=\beta\, \pi\, p_{\max} \, \bar{i}(t)\, \frac{S(t)}{P}\, ,\quad \frac{\partial I}{\partial t}(t,\tau)+\frac{\partial I}{\partial \tau}(t,\tau)=-\alpha(\tau)\, I(t,\tau)\, , \\ &&R'(t)=\int_0^\infty \alpha(\tau)\, I(t,\tau)\, d \tau - \gamma \, R(t)\, .\tag{12} \end{eqnarray} \(\bar{\Lambda}(t)\) et μ sont connus. Les seuls paramètres inconnus sont : \(P\), le produit \(\beta \, \widehat{\pi}\), le produit \(\beta \, \pi\, p_{\max}\), \(\gamma\) et les deux paramètres \(a\) et \(\nu\) qui définissent \(\alpha(\tau)\). Rappelons que pour la distribution Gamma, \(\nu/a\) est la moyenne et \(\sqrt{\nu}/a\) l'écart type.
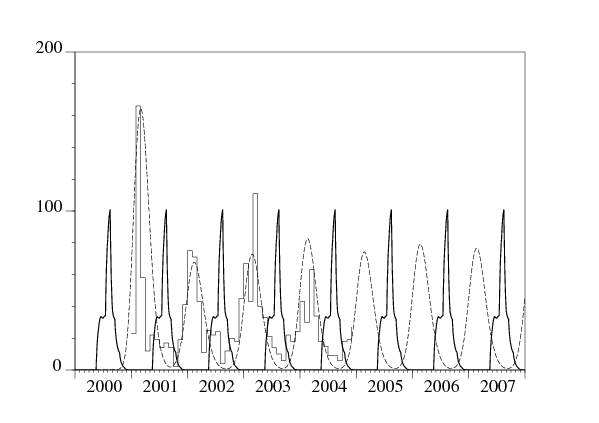
On a simulé le système (11)-(12) avec différentes valeurs de paramètres. On obtient un bon ajustement au nombre de cas rapportés chaque mois entre janvier 2001 et décembre 2004, c'est-à-dire aux données de la figure 1, avec \(P=800\), \(\beta\, \widehat{\pi}=\mbox{1,1}\) par mois, \(\beta\, \pi\, p_{\max}=16\,230\) par mois, \(1/\gamma=\mbox{1,2}\) année, \(\nu/a=6\) mois et \(\sqrt{\nu}/a=\mbox{1,5}\) mois (voir la figure 3).
En utilisant ces valeurs de paramètres, on peut calculer numériquement la reproductivité, définie dans la section précédente. Premièrement, pour simplifier l'équation (8), on utilise le changement de variable \(\theta=\tau+\sigma\). On a \[p(t) \int_0^\infty g(\tau)\, e^{\mu \tau} \int_\tau^\infty e^{-\mu \theta} w_1(t-\theta)\, d\theta\, d \tau = r_0\, w_1(t)\, .\] On intègre par parties et on remarque que le terme intégré disparaît. On arrive à \begin{equation}\tag{13} p(t) \int_0^\infty h(\tau)\, w_1(t-\tau)\, d \tau = r_0\, w_1(t)\, , \end{equation} avec \begin{equation}\tag{14} h(\tau)=e^{-\mu \tau} \int_0^\tau e^{\mu \sigma}\, g(\sigma)\, d \sigma\, . \end{equation} \(w_1(t)\) est une fonction périodique de période T. On a donc \begin{align*} \int_0^\infty h(\tau)\, &w_1(t-\tau)\, d \tau = \int_{-\infty}^t h(t-\theta)\, w_1(\theta)\, d \theta\\ &=\int_0^t h(t-\theta)\, w_1(t-\theta)\, d \theta + \sum_{n=0}^\infty \int_{0}^{T} h(t+(n+1)T-\theta)\, w_1(\theta)\, d \theta\\ &=\int_0^t H(t-\theta)\, w_1(\theta)\, d \theta + \int_t^T H(t-\theta+T)\, w_1(\theta)\, d \theta \, , \end{align*} avec \begin{equation}\tag{15} H(\tau)=\sum_{n=0}^\infty h(\tau+nT)\, . \end{equation} Donc le problème de valeur propre (13) est équivalent à \begin{equation} p(t) \Bigl \{ \int_0^t H(t-\theta)\, w_1(\theta)\, d \theta + \int_t^T H(t-\theta+T)\, w_1(\theta)\, d \theta \Bigr \} = r_0\, w_1(t)\, . \end{equation} Cette équation ne fait intervenir que les valeurs de \(w_1(t)\) sur l'intervalle \((0,T)\). On prend un entier N qui est grand. On prend \(t_i=(i-1)T/N\), \(i=1\ldots N\). On définit \(\bar{\rho}_0\), le rayon spectral du problème de valeur propre matriciel \begin{equation}\tag{16} \bar{p}(t_i)\, \frac{T}{N} \Biggl \{ \sum_{j=1}^{i-1} H(t_i-t_j)\, W_j + \sum_{j=i}^N H(t_i-t_j+T)\, W_j \Biggr \} = \bar{\rho}_0\, W_i\, . \end{equation} Ce problème est de la forme \(\mathcal{A}\, W = \bar{\rho}_0\, W\). \(\mathcal{A}\) est une matrice de taille N à coefficients positifs ou nuls et \(W=(W_1,\ldots,W_N)\). Considérons la relation (9) entre \(R_0\) et \(r_0\). On en conclut que \[\sqrt{ (\beta\, \widehat{\pi}) \times (\beta\, \pi\, p_{\max}) \times \bar{\rho}_0 / P} \mathop{\longrightarrow}_{N\to +\infty} R_0\, .\] Les résultats sont présentés dans la tableau 1.
| \(N\) | 25 | 50 | 100 | 200 | 400 |
|---|---|---|---|---|---|
| \(R_0\) | \(\mbox{1,901}\) | \(\mbox{1,926}\) | \(\mbox{1,938}\) | \(\mbox{1,940}\) | \(\mbox{1,940}\) |
En pratique, on calcule les termes de (16) de la matière suivante:
Il n'y a actuellement pas de médicament prophylactique ou de vaccin utilisables pour prévenir la leishmaniose. Les sites d'éclosion des phlébotomes sont en général inconnus. Les efforts de contrôle qui ne se concentrent que sur les stades immatures ne sont en général pas faisables (Feliciageli, 2004). Le contrôle de la leishmaniose repose donc sur les mesures prises pour réduire la densité de phlébotomes. On peut atteindre une réduction de ce genre en utilisant des insecticides. Mais la province de Chichaoua est une région rurale pauvre et cette solution nécessite probablement trop d'argent et d'effort comparé aux ressources locales. Néanmoins sa position géographique, à mi-chemin entre deux zones touristiques importantes du Maroc, Marrakech et Agadir, justifierait certainement une intervention de ce type même d'un point de vue purement économique au niveau national.
La définition de la reproductivité présentée dans ce travail se généralise de la manière suivante. On suppose que \(A(t,\tau)\) est une matrice de taille n à coefficients positifs ou nuls, qui est une fonction continue. \(A_{i,j}(t,\tau)\) représente l'espérance du nombre d'individus de type i infectés par unité de temps au temps t par un individu de type j infecté au temps t−τ. On suppose que \[A(t+T,\tau)=A(t,\tau),\quad \int_0^\infty A(t,\tau)\, d \tau < +\infty\quad \forall t.\] Avec des hypothèses convenables de positivité pour la fonction matricielle \(A(t,\tau)\), il existe un unique nombre réel \(R_0\) tel qu'il existe une fonction continue vectorielle positive, non identiquement nulle, périodique de période T, notée \(w(t)\), avec \[\int_0^\infty A(t,\tau)\, w(t-\tau)\, d\tau = R_0\, w(t)\, .\] De plus, si \(\bar{u}(t)\) est une fonction vectorielle donnée et \begin{equation}\tag{17} u(t)=\int_0^t A(t,\tau)\, u(t-\tau)\, d \tau + \bar{u}(t)\, , \end{equation} on a alors \[u(t) \sim e^{\lambda^* t}\, v(t),\quad t\to +\infty.\] \(v(t)\) est une fonction vectorielle positive, périodique de période T avec \begin{equation}\tag{18} \int_0^\infty e^{-\lambda^* \tau}\, A(t,\tau)\, v(t-\tau)\, d \tau = v(t)\, . \end{equation} Enfin, \(\lambda^* > 0\) si \(R_0 > 1\) et \(\lambda^* < 0\) si \(R_0 < 1\). Cette définition de la reproductivité peut aussi être utilisée dans d'autres champs de la dynamique des populations, par exemple la démographie où le verbe « donner naissance » remplace le verbe « infecter ».
Si on a \(A(t,\tau)=A(\tau)\), alors on prend pour \(w(t)\) un vecteur propre de la matrice \(\int_0^\infty A(\tau)\, d \tau\). \(R_0\) est donc le rayon spectral de cette matrice. Par ailleurs, \(\lambda^*\) est l'unique nombre réel pour lequel le rayon spectral de la matrice suivante est égal à 1 \[\int_0^\infty e^{-\lambda^* \tau} A(\tau)\, d \tau.\] N'importe quel vecteur propre de cette matrice associé à la valeur propre 1 peut être choisi pour \(v(t)\), de sorte que celui-ci soit solution de (18).
Il y a un autre cas particulier où la reproductivité se calcule facilement. C'est le cas où \(n=1\) et \begin{equation}\tag{19} A(t,\tau)=p(t)\, e^{-\int_{t-\tau}^t \phi(\sigma) d \sigma} \end{equation} avec des fonctions \(p(t)\) et \(\phi(t)\) qui sont périodique de période T. En effet, le problème de valeur propre sécrit \begin{equation}\tag{20} p(t) \int_0^\infty e^{-\int_{t-\tau}^t \phi(\tau) d \tau}\, w(t-\tau)\, d \tau = R_0\, w(t)\, . \end{equation} En dérivant cette équation et en intégrant par parties, on obtient \begin{align*} R_0\, w'(t) =& p'(t) \int_0^\infty e^{-\int_{t-\tau}^t \phi(\sigma) d \sigma}\, w(t-\tau)\, d \tau + p(t) \int_0^\infty e^{-\int_{t-\tau}^t \phi(\sigma) d \sigma }\, w'(t-\tau)\, d \tau \\ & + p(t) \int_0^\infty e^{-\int_{t-\tau}^t \phi(\sigma) d \sigma }\, \bigl [\phi(t-\tau) - \phi(t) \bigr ] \, w(t-\tau)\, d \tau \\ =&p'(t)\, \frac{R_0\, w(t)}{p(t)} - p(t) \int_0^\infty \phi(t-\tau)\, e^{-\int_{t-\tau}^t \phi(\sigma) d \sigma }\, w(t-\tau)\, d \tau \\ &- p(t)\, \Bigl [ e^{- \int_{t-\tau}^t \phi(\sigma) d \sigma} \, w(t-\tau) \Bigr ]_0^\infty \\ &+ p(t) \int_0^\infty e^{-\int_{t-\tau}^t \phi(\sigma) d \sigma }\, \bigl [\phi(t-\tau) - \phi(t) \bigr ] \, w(t-\tau)\, d \tau \\ =&\frac{p'(t)}{p(t)}\, R_0\, w(t) - \phi(t)\, R_0\, w(t) + p(t)\, w(t) \end{align*} Cette équation s'écrit aussi \[\frac{w'(t)}{w(t)} = \frac{p'(t)}{p(t)} - \phi(t) + \frac{p(t)}{R_0}\, .\] On a donc \begin{equation}\tag{21} w(t)=K\, p(t)\, e^{-\int_0^t \phi(\tau) d \tau + \frac{1}{R_0} \int_0^t p(\tau)\, d \tau}\, . \end{equation} K est une constante positive. \(w(t)\) est une fonction périodique si \(w(t+T)=w(t)\) pour tout t. Mais les fonctions \(p(t)\) et \(\phi(t)\) sont périodiques. \(w(t+T)=w(t)\) si et seulement si \begin{equation}\tag{22} R_0 = \frac{\int_0^T p(\tau)\, d \tau}{\int_0^T \phi(\tau)\, d \tau}\, . \end{equation} Inversement, (21) avec (22) est solution de l'équation (20). La formule (22) apparaît dans (Ma et Ma, 2006, § 3.1) pour un modèle épidémique SIR avec un taux de contact et une mortalité périodiques. L'analyse de sa stabilité linéaire se met sous la forme (17) avec \(A(t,\tau)\) de la forme (19). Mais les auteurs hésitent à utiliser la notation \(R_0\) pour le côté droit de (22). Ils utilisent \(\bar{\mathcal{R}}\), parce qu'ils n'ont pas de définition générale de la reproductivité. Cette expression n'apparaît qu'à la fin de leur analyse.
Le même calcul (dérivation, intégration par parties, etc.) en partant de (18) montre que \[v(t)= K \, p(t)\, e^{-\lambda^*\, t - \int_0^t \phi(\tau)\, d \tau + \int_0^t p(\tau)\, d \tau}\, .\] Cette fonction est périodique si et seulement si \begin{equation}\tag{23} \lambda^* = \frac{1}{T} \int_0^T p(\tau)\, d \tau - \frac{1}{T} \int_0^T \phi(\tau)\, d \tau \, . \end{equation} Le seuil épidémique (\(R_0 > 1\), ou encore \(\lambda^* > 0\)) dépend dans ce cas seulement des valeurs moyennes des coefficients. Dans le cas encore plus particulier où \(\phi(t)\) est constant, la formule (23) est le résultat « démontré » dans (Williams et Dye, 1997) en utilisant des séries de Fourier et des séries divergentes!
Mentionnons aussi que la stabilité linéaire du modèle épidémique SEIR avec un taux de contact périodique (Ma et Ma, 2006, § 2) peut se mettre sous la forme (17) avec une matrice \(A(t,\tau)\) de taille 2 semblable à celle de la section 3. Comme dans le présent article, on ne peut espérer de formule explicite pour la reproductivité mais des estimations numériques sont possibles.
Du point de vue des applications, la définition de la reproductivité que nous proposons pourrait être utilisée pour estimer le risque que des maladies à vecteurs apparaissent dans des régions non infectées jusqu'à présent. Il faut suffisamment d'information sur la population de vecteurs et sur la maladie. C'est devenu un sujet très populaire en épidémiologie car de nombreuses personnes pensent que le climat se réchauffe et que les maladies tropicales du « Sud » pourraient apparaître ou réapparaître dans le « Nord ». On mentionne en particulier le projet EDEN, « Emerging Diseases in a changing European eNvironment » (www.eden-fp6project.net).
On remercie le Dr A. Laamrani Elidrissi (Département des maladies parasitaires, Ministère de la santé publique, Rabat, Maroc) pour les données concernant les cas rapportés de leishmaniose cutanée. Une partie de ce travail a été effectué pendant que le premier auteur visitait le Laboratoire des processus stochastiques et des systèmes dynamiques de l'Université Cadi Ayyad de Marrakech au Maroc. On remercie aussi un rapporteur anonyme pour avoir signalé les références (Williams et Dye, 1997 ; Ma et Ma, 2006), qui nous ont aidés pour la section 5.