Approximation de \(R_0\) pour les maladies à vecteurs avec une population périodique de vecteurs

Résumé

1.   Introduction

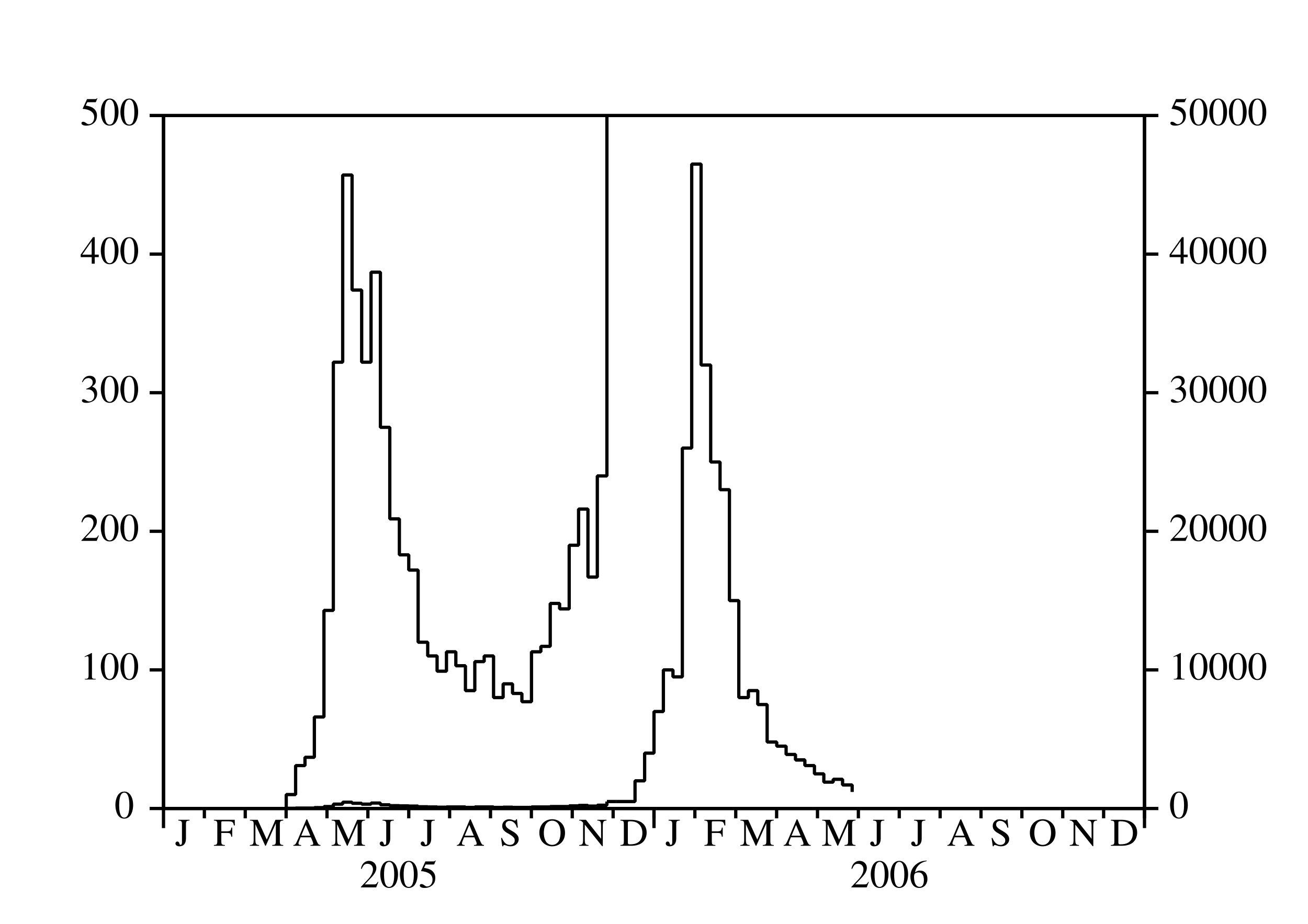
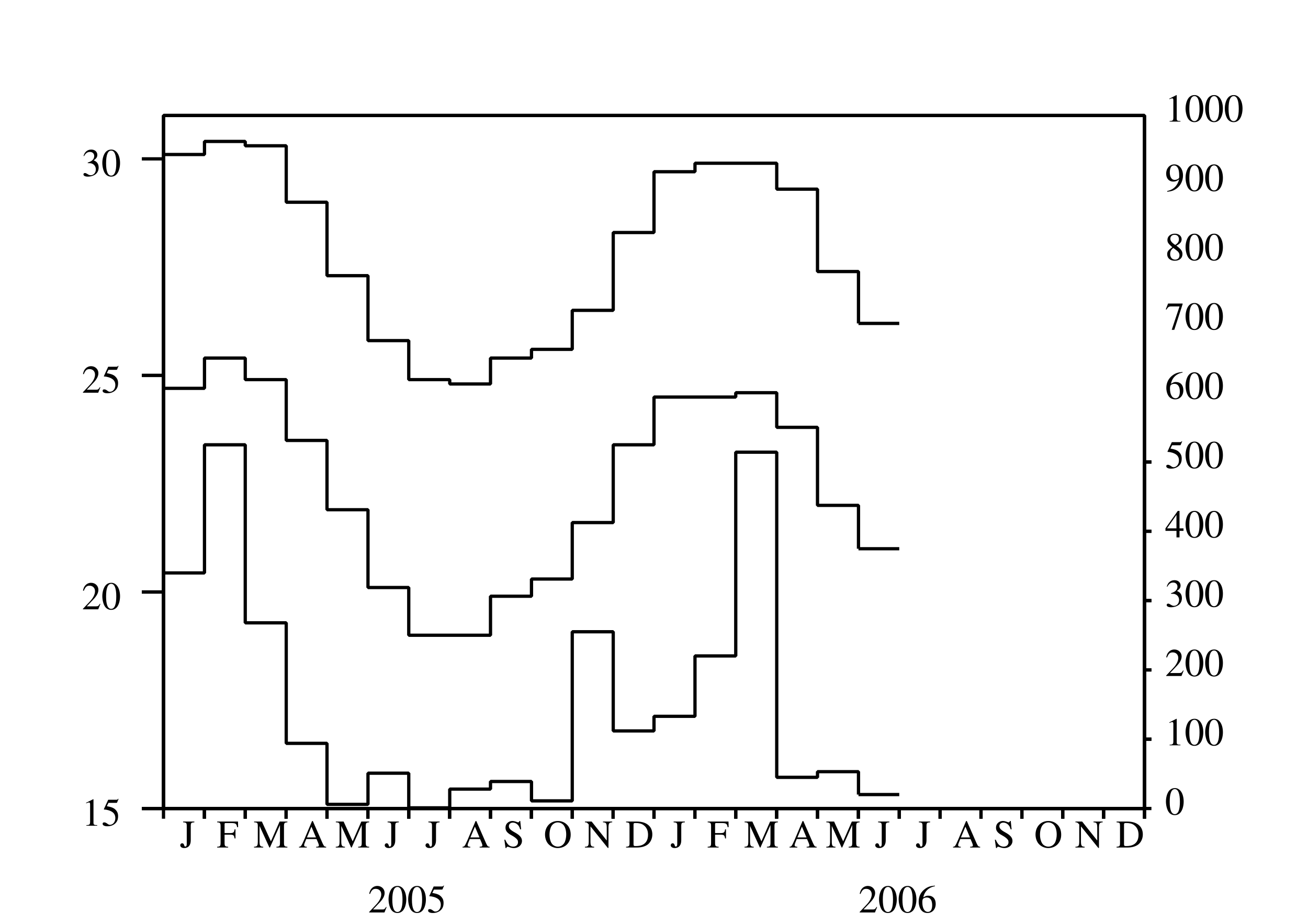
    Depuis mars 2005, une épidémie de chikungunya frappe pour la première fois l'île de La Réunion, un département français d'outre-mer situé dans l'océan Indien. Après un premier pic avec plus de 400 nouveaux cas humains par semaine en mai 2005, l'épidémie a ralenti (figure 1a). C'est à cause de l'hiver austral, qui est plus frais et moins pluvieux (figure 1b) et donc moins favorable à la prolifération d'Aedes albopictus, le moustique qui transmet le virus du chikungunya aux humains. Noter que La Réunion est dans l'hémisphère sud.

    Aedes albopictus  a été aussi responsable d'une petite épidémie de dengue qui a duré d'avril à juillet 2004, c'est-à-dire jusqu'au début de l'hiver austral (Pierre et coll., 2005). Ceci a probablement conduit les épidémiologistes locaux à croire que le scénario de l'épidémie de dengue se répéterait avec le chikungunya. Le contrôle vectoriel de petite ampleur, associé à la recherche active de cas humains, serait suffisant pour arrêter l'épidémie avant la fin de l'hiver. Cela n'a pas été le cas. Après avoir atteint un minimum inférieur à 100 nouveaux cas par semaine en septembre 2005, l'épidémie de chikungunya a recommencé à croître et a atteint un pic étonnant de 40000 nouveaux cas par semaine en février 2006. L'épidémie était alors devenue un sujet de controverse.

    Pourquoi les épidémiologistes n'avaient-ils pas été capables de prédire l'épidémie? Pourquoi le ministère de la Santé n'avait-il pas déclenché une campagne de contrôle vectoriel de grande ampleur suffisamment tôt? À présent (juillet 2006), plus de 260000 personnes ont attrapé la maladie depuis le début de l'épidémie, soit environ un tiers de la population de l'île. Environ 200 certificats de décès ont mentionné le chikungunya comme l'une des causes du décès. Par ailleurs, l'épidémie a eu un effet important sur l'économie de l'île, en particulier sur le tourisme, qui est l'une des principales industries. L'effet combiné de l'hiver et du contrôle vectoriel ont ramené à présent le nombre de nouveaux cas par semaine en dessous de mille.

    Une question importante mais difficile est de savoir si l'épidémie traversera l'hiver une nouvelle fois et causera un nouveau pic important l'été prochain. Les scientifiques ont l'habitude de penser de manière simplifiée à ce genre de question. Ils s'intéressent à un paramètre clé associé avec l'épidémie, la reproductivité, définie de manière vague comme le nombre moyen de cas secondaires causés par un premier cas au début de l'épidémie. L'épidémie se développe si  \(R_0 > 1\). L'épidémie s'arrête si \(R_0 < 1\). À la suite des travaux de Ronald Ross (1911) sur le paludisme, on a obtenu la formule suivante pour la reproductivité dans le cas des maladies à vecteurs: \begin{equation}\tag{1} R_0=\frac{\beta^2\, q\, q'\, p}{\alpha\, \mu\, P}\, . \end{equation}

•  \(\beta\) est la fréquence avec laquelle les vecteurs piquent
•  \(q\) et \(q'\) sont les probabilités de transmission pendant une piqûre du vecteur à l'humain et de l'humain au vecteur
•  \(p\) est la population de vecteurs
•  \(P\) est la population humaine
•  \(1/\alpha\) est la durée d'infection moyenne chez les humains
•  \(1/\mu\) est l'espérance de vie des vecteurs adultes.

    Dans cet article, on se concentre sur la partie plus théorique du problème, à savoir l'estimation de la reproductivité. Un aspect frappant de l'épidémie de chikungunya est sa saisonnalité. La formule (1) suppose que la population de vecteurs est constante tout au long de l'année. Plusieurs questions se posent: comment définir la reproductivité si l'on prend en compte la saisonnalité, par exemple si l'on suppose que la population de vecteurs est une fonction périodique du temps ? Comment calculer cette reproductivité ? Y-a-t-il des cas particuliers où l'on peut obtenir une formule simple semblable à (1)?

    Ces questions ne sont évidemment pas spécifiques au chikungunya. Elles se posent par exemple pour d'autres maladies à vecteurs. Plus généralement, ces questions se posent pour les problèmes de dynamique des populations avec de la saisonnalité, comme en épidémiologie (Altizer et coll., 2006), en écologie, en démographie, en immunologie, et en génétique des populations.

    Un travail récent (Bacaër et Guernaoui, 2006) a commencé à répondre à quelques unes de ces questions. Il contient une définition de la reproductivité dans un environnement périodique comme rayon spectral d'un opérateur linéaire intégral sur un espace de fonctions périodiques. La définition est inspirée par des travaux antérieurs sur la dynamique des populations structurées par âge avec coefficients périodiques (Coale, 1972 ; Thieme, 1984 ; Jagers et Nerman, 1985 ; Anita et coll., 1998) et par le livre de Diekmann et Heesterbeek (2000), qui met en avant la notion de « matrice de prochaine génération » et d'« opérateur de prochaine génération » pour définir la reproductivité. (Bacaër et Guernaoui, 2006) contient aussi un algorithme basé sur la discrétisation de l'opérateur intégral. On a utilisé cet algorithme pour estimer la reproductivité lors d'une épidémie de leishmaniose au Maroc. On connaissait avec précision les fluctuations de la population de vecteurs grâce à des enquêtes de terrain.

    Notre article s'organise de la manière suivante. Dans la section 2, on introduit une petite modification de la définition de la reproductivité donnée par (Bacaër et Guernaoui, 2006, §5). On nomme ici \(r_0\) le rayon spectral de « l'opérateur de prochaine génération », tandis que \(R_0=r_0^n\). n est le nombre de compartiments infectés du modèle. (Heesterbeek et Roberts, 1995b, §2.1) a déjà discuté brièvement de ce point dans le cas des « matrices de prochaine génération ». On montre aussi pour une certaine classe de modèles, que l'on nomme « cycliques », que le problème intégral de valeur propre en dimension n se réduit à un problème unidimensionnel. Par la suite, on s'intéresse au cas particulier où le noyau du problème réduit est  \(K(x,t)=f(t)\, G(x)\).  \(f(t)\) est une fonction périodique. Ce cas inclut déjà de nombreux modèles de maladies à vecteurs et de maladies transmises directement.

    Dans la section 3, on présente quatre méthodes numériques pour le calcul de la reproductivité dans des problèmes intégraux de valeur propre unidimensionnels. La première méthode est celle déjà présentée dans (Bacaër et Guernaoui, 2006, §4): c'est une simple discrétisation de l'opérateur intégral. La seconde méthode utilise les séries de Fourier et s'inspire de (Williams et Dye, 1997), qui étudie le paramètre malthusien et non la reproductivité . Ces deux méthodes marchent pour une fonction générale \(G(x)\) et une fonction périodique \(f(t)\). La troisième méthode ne concerne que le cas particulier où  \(f(t)=1+\varepsilon \cos(\omega t - \phi)\). Cette méthode combine des séries de Fourier avec une méthode de perturbation. Elle ressemble à celle de (Coale, 1972, chapitre 6), qui s'intéresse également au paramètre malthusien et non à la reproductivité . La quatrième méthode marche pour les opérateurs de prochaine génération cycliques associés aux systèmes linéaires d'équations différentielles ordinaires à coefficients périodiques. La méthode utilise la théorie de Floquet comme dans (Heesterbeek et Roberts, 1995a, 1995b) mais d'une manière différente.

    Dans la section 4, on considère des maladies à vecteurs et l'on suppose que la population de vecteurs est donnée par la formule suivante \begin{equation}\tag{2} p(t) = p_0 \bigl [1 +\varepsilon \cos\bigl (\omega t-\phi \bigr ) \bigr ]\, . \end{equation} En utilisant tout d'abord un modèle simple pour le paludisme et les résultats de la section 3.3, on montre qu'avec les mêmes notations que dans (1), la reproductivité est donnée par \begin{equation}\tag{3} R_0 \simeq \frac{\beta^2\, q\, q' \, p_0}{\alpha\, \mu\, P} \Bigl ( 1 - \frac{\alpha \mu}{\omega^2 + (\alpha+\mu)^2}\ \frac{\varepsilon^2}{2} \Bigr ), \quad \varepsilon\to 0. \end{equation} Cette formule apparemment nouvelle généralise la formule (1). Le premier terme est semblable au cas d'une population constante de vecteurs mais avec la population remplacé par sa moyenne. La correction relative maximale due au second terme est \(\varepsilon^2/8\) et tend toujours à diminuer la reproductivité. On se tourne ensuite vers l'épidémie de chikungunya en utilisant un modèle légèrement plus compliqué. La forme simplifiée (2) pour la population de vecteurs ne semble pas trop déraisonnable quand on regarde les courbes de température et de précipitations à La Réunion (figure 1b). Les deux n'ont qu'un maximum chaque année vers février. Après avoir estimé les paramètres de ce modèle, on compare les quatre méthodes numériques de la section 3 pour le calcul de la reproductivité. Cependant on ne devrait pas trop prendre au sérieux la valeur numérique ainsi obtenue pour la reproductivité de l'épidémie de chikungunya. Les valeurs des paramètres ne sont pas connues précisément. L'hypothèse (2) est simpliste. On peut voir cela comme un exercice pour tester les différentes méthodes numériques. C'est une source d'inspiration pour développer la théorie. C'est une première tentative de modélisation en attendant des études de terrain sur les fluctuations de la population de moustiques.

    La dernière section discute de l'applicabilité de la méthode de la section 3.3 pour obtenir des formules approchées pour la reproductivité dans le cadre d'autres modèles mathématiques de maladies infectieuses avec coefficients périodiques, en particulier pour le modèle SIR avec un taux périodique de contacts et une période infectieuse fixe, et aussi pour le modèle SEIR avec un taux périodique de contacts et des périodes de latence et d'infectiosité distribuées exponentiellement. On présente aussi des indications préliminaires sur la signification de la reproductivité dans les modèles épidémiques stochastiques avec saisonnalité.

2.   Définition de \(R_0\)

    Avec \(t \in \mathbb{R}\) et \(x\geq 0\), on suppose que \(K(t,x)\) est une matrice de taille n à coefficients positifs ou nuls. On supposons que \(K(t+\theta,x)=K(t,x)\) si \(x\geq 0\).

    L'idée derrière la fonction \(K(t,x)\) est celle d'un modèle épidémique avec n compartiments infectés  \((I_1,I_2,\ldots,I_n)\). Ces compartiments peuvent être infectieux ou latents.  \(K_{i,j}(t,x)\) représente l'espérance du nombre d'individus de type i qu'un individu de type j infecte au début d'une épidémie par unité de temps au temps t, s'il est de type j depuis x unités de temps. Cela couvre le cas où des individus de type j infectent des individus qui se retrouvent de type i mais aussi le cas où des individus de type j changent simplement de compartiment pour se retrouver de type i. L'hypothèse de périodicité pour le noyau K représente un environnement périodique.

    Considérons l'opérateur linéaire intégral  \(\mathcal{K}\) défini par \begin{equation}\tag{4} (\mathcal{K}v)(t)=\int_0^\infty K(t,x)\, v(t-x)\, dx \end{equation} sur un espace de fonctions périodiques de période θ à valeurs dans \(\mathbb{R}^n\). Pour être plus précis, on remarque qu'avec les hypothèses de périodicité sur le noyau K et la fonction v, l'équation (4) peut s'écrire \[(\mathcal{K}v)(t)=\int_0^\theta \widehat{K}(t,s)\, v(s)\, ds\] avec \[\widehat{K}(t,s)=\left \{\begin{array}{ll} \sum_{k=0}^{+\infty} K(t,t-s+k\, \theta), & \quad s < t,\\ \sum_{k=1}^{+\infty} K(t,t-s+k\, \theta), & \quad s > t. \end{array} \right.\] On supposons  \(\widehat{K}\in L^2((0,\theta) \times (0,\theta),\mathbb{R}^{n\times n})\). Une simple extension de (Hochstadt, 1973, théorème 7, p. 51) montre que \(\mathcal{K}\) est un opérateur linéaire compact de \(L^2( (0,\theta),\mathbb{R}^n)\to L^2( (0,\theta),\mathbb{R}^n)\). Comme dans (Diekmann et Heesterbeek, 2000, p. 77), on peut le nommer l'opérateur linéaire de prochaine génération. \(K(t,x)\) est le noyau associé.  \(r_0\) est le rayon spectral de  \(\mathcal{K}\). On définit la reproductivité par la formule \(R_0=r_0^n\). Voir (Heesterbeek et Roberts, 1995b, §2.1) pour une discussion de pourquoi il est parfois plus commode de prendre  \(R_0=r_0^n\) que \(R_0=r_0\). Voir aussi (Bacaër et Guernaoui, 2006, §5) pour une discussion de pourquoi cette définition de la reproductivité généralise la définition habituelle sans saisonnalité avec la matrice de prochaine génération (Diekmann et Heesterbeek, 2000, p. 74).

    L'opérateur linéaire \(\mathcal{K}\) est positif. Dans le cas \(r_0 > 0\), le théorème de \(\text{Krein}\) et Rutman (Krasnosel'skij et coll., 1980, théorème 9.2, p. 87) montre que  \(r_0\) est une valeur propre de \(\mathcal{K}\) et qu'il existe une fonction propre positive \(v\in L^2((0,\theta),\mathbb{R}^n)\) associée à \(r_0\). En étendant v par périodicité à  \(\mathbb{R}\), on peut écrire \begin{equation}\tag{5} \int_0^\infty K(t,x)\, v(t-x)\, dx = r_0\, v(t)\, . \end{equation} (Krasnosel'skij et coll., 1980) et (Schaefer, 1974, p. 377) donnent des conditions qui assurent que \(r_0 > 0\).

    Dans le reste de cet article, on considère des modèles « cycliques » qui ont la forme particulière suivante (figure 2): tous les éléments \(K_{i,j}(t,x)\) du noyau sont nuls sauf \(K_{1,n}(t,x)\) et \(K_{j+1,j}(t,x)\) avec  \(1\leq j\leq n-1\).

    Ceci inclut en particulier le cas général unidimensionnel n=1 avec un noyau arbitraire K. Avec \(v(t)=(v_1(t),\ldots,v_n(t))\), le problème intégral (5) s'écrit \begin{eqnarray*} \int_0^\infty K_{1,n}(t,x)\, v_n(t-x)\, dx &=& r_0\, v_1(t),\\ \int_0^\infty K_{j+1,j}(t,x)\, v_j(t-x)\, dx &=& r_0\, v_{j+1}(t),\quad 1\leq j \leq n-1. \end{eqnarray*} On remplace successivement l'équation avec  \(j=n-1\), \(j=n-2\), \(\ldots\) \(j=1\) dans la première équation. Avec \(R_0=r_0^n\), on a \begin{align*} \int_0^\infty\!\!\!\!\!\cdots \int_0^\infty &K_{1,n}(t,x_1)\, K_{n,n-1}(t-x_1,x_2) \cdots\, K_{2,1}(t-x_1-\cdots-x_{n-1},x_n)\\ &v_1(t-x_1-\cdots - x_n)\, dx_1\cdots dx_n = R_0\, v_1(t). \end{align*} Il faut noter une propriété importante: si un élément non nul de K est multiplié par une certaine constante, alors la reprodctivité est aussi multipliée par la même constante. Le changement de variable \((x_1=x_1,\ldots,x_{n-1}=x_{n-1},x=x_1+\cdots+x_n)\) conduit à \begin{equation}\tag{6} \int_0^\infty \widetilde{K}(t,x)\, v_1(t-x)\, dx = R_0\, v_1(t). \end{equation}  \(\widetilde{K}(t,x)\) est l'intégrale d'hypersurface \[\widetilde{K}(t,x) = \int_{\sigma_x^n} \!\!\!K_{1,n}(t,x_1)\, K_{n,n-1}(t-x_1,x_2) \cdots\, K_{2,1}(t-x_1-\cdots-x_{n-1},x_n)\, d\sigma_x^n\] et \(\sigma_x^n=\{(x_1,\ldots,x_n) \in \mathbb{R}^n; x_1+\cdots+x_n = x, x_1\geq 0, \ldots, x_n \geq 0\}\). Ainsi on a réduit le problème intégral (5) de valeur propre de dimension n à un problème unidimensionnel (6).

    Dans le reste de l'article sauf dans la section 3.4, on considère le cas particulier où \begin{equation}\tag{7} K_{1,n}(t,x)=f(t)\, g_n(x),\quad K_{j+1,j}(t,x)=g_j(x),\ 1\leq j\leq n-1. \end{equation} L'équation (6) devient \begin{equation}\tag{8} f(t) \int_0^\infty G(x)\, v_1(t-x)\, dx = R_0\, v_1(t), \end{equation} avec \begin{equation}\tag{9} G(x)=\int_{\sigma_x^n} g_1(x_1) \cdots g_n(x_n)\, d\sigma_x. \end{equation} Noter que si n=1, le noyau se réduit à  \(K(t,x)=f(t)\, g_1(x)\) et  \(G(x)=g_1(x)\). Noter aussi que si \begin{equation}\tag{10} g_j(x)=a_j\, e^{-b_j\, x}, \quad 1\leq j\leq n, \end{equation} on peut montrer (voir appendice) en partant de (9) que \begin{equation}\tag{11} G(x)=a_1 \cdots a_n \sum_{j=1}^n \frac{e^{-b_j\, x}}{\prod_{k\neq j} (b_k-b_j)}\, . \end{equation} Cette formula reste valable pour \(n=1\) avec la convention usuelle que le produit sur un ensemble vide est égal à 1.

3.   Méthodes numériques pour calculer la reproductivité

3.1   Discrétisation du problème intégral de valeur propre

    Cette méthode consiste à discrétiser le problème intégral (8). Elle est présentée dans (Bacaër et Guernaoui, 2006, §4); on ne la rappelle donc que brièvement. On prend un entier N très grand et  \(t_k=(k-1)\, \theta /N\), avec  \(k=1,2,\ldots,N\). On définit \begin{equation}\tag{12} \widehat{G}(x)=\sum_{k=0}^{+\infty} G(x+k\, \theta). \end{equation} \(\mathcal{R}_0\) est le rayon spectral de la matrice du problème de valeur propre \begin{equation}\tag{13} f(t_k)\, \frac{\theta}{N} \Bigl [\sum_{j=1}^{k-1} \widehat{G}(t_k-t_j)\, \mathcal{V}_j + \sum_{j=k}^{N} \widehat{G}(t_k-t_j+\theta)\, \mathcal{V}_j \Bigr ] = \mathcal{R}_0\, \mathcal{V}_k\ . \end{equation}  \(\mathcal{V}_i\) est un vecteur propre. On a alors  \(\mathcal{R}_0\to R_0\) si \(N\to +\infty\). Le calcul numérique de \(\mathcal{R}_0\) peut se faire avec Scilab (www.scilab.org), un logiciel libre semblable à Matlab. Noter que si  \(g_j(x)=a_j\, e^{-b_j\, x}\),  \(1\leq j\leq n\), il résulte de (11) que \begin{equation}\tag{14} \widehat{G}(x)=a_1 \cdots a_n \sum_{j=1}^n \frac{e^{-b_j\, x}}{(1-e^{-b_j\, \theta})\, \prod_{i\neq j} (b_i-b_j)}\, . \end{equation}

3.2   Séries de Fourier : cas général périodique

    La décomposition de Fourier d'une fonction périodique donne \begin{equation}\tag{15} f(t)=\sum_{j\in \mathbb{Z}} f_j\, e^{j i \omega t},\quad f_j=\frac{1}{\theta} \int_0^\theta f(t)\, e^{-j i \omega t}\, dt\, , \quad \omega=2\pi/\theta. \end{equation} \(\mathbb{Z}\) est l'ensemble des entiers (positifs ou négatifs) et \(i^2=-1\).  \(f_j\) est un nombre complexe avec \(f_{-j}=f_j^*\). \(^*\) désigne le nombre complexe conjugué. On cherche une solution de (8) qui est une fonction réelle et même positive \begin{equation}\tag{16} v_1(t)=\sum_{j \in \mathbb{Z}} c_j\, e^{j i \omega t}. \end{equation}  \(c_j\) est aussi un nombre complexe avec \(c_{-j}=c_j^*\). On remplace (15) et (16) dans (8): \begin{equation}\tag{17} \Bigl (\sum_{j \in \mathbb{Z}} f_j\, e^{j i\omega t}\Bigr ) \Bigl ( \sum_{j \in \mathbb{Z}} G_j \, c_j \, e^{j i \omega t} \Bigr )= R_0 \sum_{j \in \mathbb{Z}} c_j\, e^{j i \omega t}\, , \end{equation} avec \begin{equation}\tag{18} G_j=\int_0^\infty G(x)\, e^{- j i \omega x}\, dx\, . \end{equation} Il résulte de (9) que \begin{equation}\tag{19} G_j= \Bigl (\int_0^\infty g_1(x)\, e^{-j i \omega x}\, dx \Bigr ) \cdots \Bigl (\int_0^\infty g_n(x)\, e^{-j i \omega x}\, dx \Bigr ). \end{equation} Dans le cas \(g_j(x)=a_j\, e^{-b_j\, x}\) si  \(1\leq j\leq n\), on a alors \begin{equation}\tag{20} G_j = \frac{a_1 \cdots a_n}{(b_1+j i \omega) \cdots (b_n + j i \omega)}, \quad \forall j\in \mathbb{Z}. \end{equation} L'équation (17) peut s'écrire \[ \sum_{j \in \mathbb{Z}} \Bigl ( \sum_{k \in \mathbb{Z}} f_{j-k}\, G_k\, c_k \Bigr ) e^{j i \omega t} = R_0 \sum_{j \in \mathbb{Z}} c_j\, e^{j i \omega t} .\] Cette égalité est vraie si et seulement si \begin{equation}\tag{21} \sum_{k \in \mathbb{Z}} f_{j-k}\, G_k\, c_k = R_0\, c_j , \quad \forall j\in \mathbb{Z}. \end{equation} C'est un problème de valeur propre pour une matrice infinie. Noter que \(f_k \to 0\) et \(G_k \to 0\) si \(k \to \pm \infty\). Donc si on laisse N grandir et si  \(\mathcal{R}_0\) est le rayon spectral de la matrice carrée tronquée  \((f_{j-k}\, G_k)_{-N\leq j,k \leq N}\), on a alors \(\mathcal{R}_0\to R_0\) si \(N\to +\infty\).

3.3   Séries de Fourier : le cas sinusoïdal

    On suppose que \begin{equation}\tag{22} f(t)=1+\varepsilon \cos \bigl (\omega t-\phi \bigr ), \quad 0\leq \varepsilon \leq 1, \quad 0\leq \phi < 2\pi. \end{equation} C'est ce que l'on appelle une fonction sinusoïdale. Pour le problème de valeur propre (8), un décalage dans le temps de la fonction f ne change pas la reproductivité. En effet, si \(R_0\) est le rayon spectral pour la fonction f avec la fonction propre  \(v_1(t)\),  \(R_0\) est encore le rayon spectral pour la fonction \(\hat{f}(t)=f(t-h)\) avec la fonction propre  \(\hat{v}_1(t)=v_1(t-h)\). Pour le calcul de la reproductivité, on peut donc supposer  \(\phi=0\) et \[ f(t)=1 + \frac{\varepsilon}{2}\, e^{i\omega t} + \frac{\varepsilon}{2}\, e^{-i\omega t}. \] De manière évidente, on a \[f_0=1,\quad f_1=f_{-1}=\frac{\varepsilon}{2},\quad f_k=0\quad \forall \, |k| > 1.\] Le système (21) devient \begin{equation}\tag{23} \frac{\varepsilon}{2} \, G_{j-1}\, c_{j-1} + G_j\, c_j + \frac{\varepsilon}{2}\, G_{j+1}\, c_{j+1} = R_0\, c_j , \quad \forall j\in \mathbb{Z}. \end{equation} \(G_{-j}=G_j^*\) parce que la fonction \(G(x)\) est à valeurs réelles. L'équation (23) avec \(c_{-j}\) dans le côté droit est simplement le complexe conjugué de l'équation (23) avec  \(c_j\) dans le côté droit. On peut donc oublier l'équation (23) pour j<0. On a \(c_{-1}=c_1^*\) et \(G_{-1}=G_1^*\). Le problème de valeur propre (23) avec  \(j\in \mathbb{Z}\) se réduit au système suivant \begin{equation}\left \{\begin{array}{ccccccl} \frac{\varepsilon}{2}\, G_1^*\, c_1^* &+& G_0\, c_0 &+& \frac{\varepsilon}{2}\, G_1\, c_1 &= &R_0 \, c_0\, ,\\ \frac{\varepsilon}{2}\, G_{j-1}\, c_{j-1} &+& G_j\, c_j &+& \frac{\varepsilon}{2}\, G_{j+1}\, c_{j+1} &=& R_0\, c_j\, ,\ (j\geq 1). \end{array}\right. \tag{24} \end{equation} La fonction  \(v_1(t)\) peut être normalisée de sorte que \(c_0=1\). C'est possible parce que \(v_1(t)\) est strictement positif et  \(c_0=\frac{1}{\theta} \int_0^\theta v_1(t)\, dt > 0\). Cherchons une solution du système (24) de la forme \begin{equation}\tag{25} R_0=\sum_{k\geq 0} \rho_{k}\, \varepsilon^k,\quad c_j=\sum_{k\geq 0} c_{j,k}\, \varepsilon^k, \end{equation} dont on attend qu'elle soit valable au moins pour de petites valeurs de ε. Avec \(c_0=1\), on a \(c_{0,0}=1\) et \(c_{0,k}=0\) si k≥1. On insère (25) dans la première équation de (24) et l'on sépare les puissances de \(\varepsilon^k\). On obtient  \(G_0 = \rho_{0}\) et \begin{equation}\tag{26} \frac{G_1^*}{2}\, c_{1,k-1}^* + \frac{G_1}{2}\, c_{1,k-1} = \rho_{k},\quad \forall k\geq 1. \end{equation} De même, en insérant (25) dans la seconde équation de (24), on arrive à \[G_j\, c_{j,0} = \rho_{0}\, c_{j,0},\quad \forall j\geq 1\] et \begin{equation}\tag{27} \frac{G_{j-1}}{2}\, c_{j-1,k-1} + G_j\, c_{j,k} + \frac{G_{j+1}}{2}\, c_{j+1,k-1} = \sum_{l=0}^k \rho_{l}\, c_{j,k-l},\quad \forall j\geq 1,\ \forall k\geq 1. \end{equation} On a  \((G_0-G_j)\, c_{j,0} =0,\ \forall j\geq 1\). On a donc  \(c_{j,0}=0\) parce que \(G(x)\) est positif et non identiquement nul de sorte que  \(G_0-G_j=\int_0^\infty (1-e^{-ji\omega x})\, G(x)\, dx\neq 0\). Avec \[\rho_{0}= G_0,\quad c_{j,0}=0\ (j\geq 1),\quad c_{0,0}=1,\quad c_{0,k}=0\ (k\geq 1),\] on voit avec (26) et (27) que les coefficients \(\rho_{k}\) et \(c_{j,k}\) se calculent récursivement: \begin{eqnarray} \rho_{k} &=& \Re ( G_1\, c_{1,k-1})\, \quad \forall k\geq 1,\tag{28}\\ c_{j,k} &=& \frac{1}{G_0-G_j} \Bigl [ \frac{G_{j-1}}{2}\, c_{j-1,k-1} + \frac{G_{j+1}}{2}\, c_{j+1,k-1} - \sum_{l=1}^{k-1} \rho_{l}\, c_{j,k-l} \Bigr ], \quad \forall j\geq 1,\ \forall k\geq 1.\tag{29} \end{eqnarray} \(\Re(z)\) désigne la partie réelle du nombre complexe z. Plus précisément, si les coefficients \(\rho_l\) et \(c_{j,l}\) sont calculés pour  \(l\leq k-1\) et \(j\geq 1\), alors les formules donnent une expression pour \(\rho_k\) et \(c_{j,k}\) avec \(j\geq 1\). Cet algorithme peut démarrer parce que \(\rho_0\) et les coefficients \(c_{j,0}\) sont connus. En utilisant (28)-(29), on a

•  \(c_{j,k}=0\) pour tout j>k,
•  \(\rho_k=0\) pour tout nombre impair k,
•  \(c_{j,k}=0\) si  \(j\geq 1\) est un nombre impair alors que \(k\geq 1\) est un nombre pair.

    En pratique, fixons un entier \(\kappa > 1\) et considérons le vecteur \((\rho_k)_{0\leq k\leq \kappa}\) et la matrice rectangulaire  \((c_{j,k})_{0\leq j\leq \kappa+1,\, 0\leq k\leq \kappa}\). On met \(\rho_0= G_0\), \(c_{0,0}=1\), \(c_{j,k}=0\) avec \(j > k\) dans la matrice, et  \(c_{0,k}=0\) si \(1\leq k\leq \kappa\). L'algorithme fonctionne ainsi:

    De cette manière, on voit facilement que \begin{equation}\tag{30} \rho_1=0,\quad c_{1,1}=\frac{G_0}{2(G_0-G_1)},\quad \rho_2=\frac{1}{2}\, \Re \Bigl (\frac{G_0\, G_1}{G_0-G_1} \Bigr ), \end{equation} Finalement on trouve \begin{equation}\tag{31} R_0 \simeq G_0 + \frac{\varepsilon^2}{2}\, \Re \Bigl (\frac{G_0\, G_1}{G_0-G_1} \Bigr ),\quad \varepsilon \to 0. \end{equation} C'est la correction d'ordre le plus bas à la reproductivité lorsque des variations saisonnières de petite amplitude sont prises en compte. Faisons quelques remarques additionnelles:

• On a \[1 -\varepsilon \cos \bigl ( \omega t-\phi \bigr ) = 1 +\varepsilon \cos \bigl ( \omega (t+ \theta/2) - \phi \bigr ) .\] Ainsi, changer ε en −ε correspond à un décalage temporel de \(f(t)\). Donc d'après la remarque faite au début de la section 3.3, la reproductivité doit rester inchangé. Ceci explique pourquoi les coefficients impairs \(\rho_{2k+1}\) dans le développement en série de la reproductivité sont nuls.
• La fonction sinusoïdale (22) n'est pas aussi particulière qu'il semblerait à première vue. En effet, pour toute fonction positive périodique f, avec par exemple une moyenne égale à 1, les premiers termes du développement de Fourier sont \[1 + f_1 \cos (\omega t) + f_1' \sin (\omega t)=1+\varepsilon \cos (\omega t - \phi)\] avec  \(\varepsilon = \sqrt{(f_1)^2+(f'_1)^2}\) et \(\phi = \arctan (f'_1/f_1)\).
• Il semble difficile de déterminer les rayons de convergence de (25). Des théorèmes généraux sur les perturbations analytiques des opérateurs linéaires (Kato, 1984) montrent que ces rayons de convergence sont strictement positifs, parce que \(r_0\) est une valeur propre simple et isolée. (Kato, 1984) a aussi développé des méthodes non triviales pour obtenir des bornes inférieures pour ces rayons: un travail supplémentaire est nécessaire pour essayer de les appliquer dans le cas présent. En pratique, l'algorithme de cette section donne facilement \(\rho_k\) pour k≤20 ou k≤50. Si l'on observe que  \(\rho_k\) converge vers 0 quand \(k\to +\infty\), alors il y a de bonnes chances que le rayon de convergence de la série pour la reproductivité soit supérieur ou égal à 1.
• La méthode de perturbation formelle utilisée dans cette section peut être considérée du point de vue de la théorie mathématique générale développée par (Kato, 1984). Considérons par exemple le côté gauche de (8), avec la fonction f donné par (22), comme un opérateur linéaire  \(\mathcal{L}_\varepsilon\) sur l'espace de Hilbert des fonctions réelles périodiques, dont le carré est intégrable. Le produit scalaire est \[\langle \psi_1,\psi_2\rangle = \int_0^\theta \psi_1(t)\, \psi_2(t)\, dt.\] Considérons le problème de valeur propre non perturbé \(\mathcal{L}_0\, \psi = \lambda\, \psi\), c'est-à-dire \[ \int_0^\infty G(x)\, \psi(t-x)\, dx = \lambda\, \psi(t)\, .\] On cherche une solution \[\psi(t)=\sum_{k\in \mathbb{Z}} a_k\, e^{k i \omega t}.\] On obtient \[(\lambda- G_k)\, a_k=0,\, \forall k.\] Donc les valeurs propres sont données par \(\lambda_k=G_k,\quad \forall \, k\in \mathbb{Z}\). Le sous-espace associé est engendré par \[\psi_k(t)=e^{k i \omega t}.\] Les fonctions \(\psi_k\) forment une base. Considérons la base duale \[\widehat{\psi}_k(t)=\frac{e^{-k i \omega t}}{\theta},\quad k\in \mathbb{Z},\] avec \(\langle \psi_j, \widehat{\psi}_k \rangle = 1\) si j=k et 0 si j≠k. On a \[\mathcal{L}_\varepsilon = \mathcal{L}_0 + \varepsilon \, \mathcal{L}',\] \[(\mathcal{L}'\psi)(t) = \cos(\omega t -\phi)\int_0^\infty G(x)\, \psi(t-x)\, dx\, .\] On s'intéresse à la perturbation \(R_0=\rho_0+\varepsilon\, \rho_{1} + \varepsilon^2\, \rho_{2} + \cdots\) pour la valeur propre \(\lambda_0=\rho_0=G_0\), dont la fonction propre associée  \(\psi_0=1\) est positive. On utilise les formules données par (Kato, 1984, p. 81) en dimension finie. Ces formules restent valides en dimension infinie et sont bien connues en mécanique quantique pour les opérateurs autoadjoints (Cohen-Tannoudji et coll., 1986, chapitre XI). On obtient \[ \rho_{1}=\langle \mathcal{L}' \psi_0,\widehat{\psi}_0\rangle = \frac{G_0}{\theta} \int_0^\theta \cos(\omega t - \phi)\, dt = 0\, , \] et \begin{align*} \rho_{2}&=\sum_{k\neq 0} \frac{ \langle \mathcal{L}' \psi_0,\widehat{\psi}_k\rangle \langle \mathcal{L}' \psi_k,\widehat{\psi}_0\rangle }{\lambda_0-\lambda_k} \\ &=\frac{1}{\theta^2} \sum_{k\neq 0} \frac{G_0\, G_k}{G_0-G_k}\, \Bigl | \int_0^\theta \cos(\omega t - \phi) e^{k i \omega t}\, dt\Bigr |^2 =\frac{1}{2}\, \Re \Bigl (\frac{G_0\, G_1}{G_0-G_1} \Bigr ), \end{align*} qui est identique à (30). Les expressions pour les corrections d'ordre supérieur sont plus compliquées: la méthode et l'algorithme ad hoc que l'on a utilisés pour calculer  \(\rho_k\) semblent plus pratiques.

3.4   Application de la théorie de Floquet

    Dans cette section, on considère le système linéaire d'équations différentielles ordinaires \begin{align} \frac{dI_1}{dt} &= -\alpha_1(t)\, I_1(t) + \beta_n(t)\, I_n(t),\tag{32}\\ \frac{dI_{j+1}}{dt} &= -\alpha_{j+1}(t)\, I_{j+1}(t)+ \beta_{j}\, I_{j}(t),\quad 1\leq j\leq n-1, \tag{33} \end{align} où toutes les fonctions \(\alpha_j(t)\) et \(\beta_j(t)\) sont périodiques avec la même période θ. Ce système peut venir de la linéarisation près de l'équilibre sans maladie d'un modèle épidémique non linéaire. Le noyau de l'opérateur de prochaine génération associé est donné par \begin{align*} K_{1,n}(t,x)&=\beta_n(t)\, e^{-\int_{t-x}^t \alpha_n(s)\, ds},\\ K_{j+1,j}(t,x)&=\beta_j(t)\, e^{-\int_{t-x}^t \alpha_{j+1}(s)\, dx},\quad 1\leq j \leq n-1, \end{align*} et \(K_{i,j}(t,x)=0\) pour tous les autres indices. C'est donc un modèle « cyclique » au sens de la section 2. Une remarque dans cette section montre que si par exemple \(\beta_n(t)\) est multiplié par une certaine constante, alors la reproductivité est multiplié par la même constante.

    La théorie de Floquet appliquée au système (32)-(33) montre que l'équilibre nul est instable si et seulement si le rayon spectral de la « matrice de prochaine année », aussi appelée matrice de monodromie, est supérieur à 1.

    La reproductivité est donc aussi l'unique nombre réel positif, pour lequel  \(\rho(X(\theta))=1\).  \(\rho\) est le rayon spectral de la matrice et \[\frac{dX}{dt}(t)=\left (\begin{array}{ccccc} -\alpha_1(t) & 0 & \cdots & 0 & \frac{\beta_n(t)}{R_0} \\ \beta_1(t) & \ddots & \ddots & & 0\\ 0 & \ddots & \ddots & \ddots & \vdots \\ \vdots & \ddots & \ddots & \ddots & 0\\ 0 & \cdots & 0 & \beta_{n-1}(t) & -\alpha_n(t) \end{array}\right ) X(t)\] avec la condition initiale  \(X(0)=1_n\) (la matrice identité de taille n).  \(R_0\) se calcule avec une méthode de dichotomie. On utilise un logiciel tel que Scilab pour résoudre numériquement les équations différentielles ordinaires.

4.   Les maladies à vecteurs

4.1   Le paludisme

    On considère dans cette section un modèle très simple pour le paludisme, à savoir une variation sur l'un des premiers modèles proposés par Ronald Ross (1911) avec une population périodique de vecteurs. Introduisons les notations suivantes:

•  \(S(t)\) est la population humaine saine
•  \(I(t)\) est la population humaine infectée
•  \(P=S(t)+I(t)\) est la population humaine totale
•  \(s(t)\) est la population vectorielle saine
•  \(i(t)\) est la population vectorielle infectée
•  \(p(t)=s(t)+i(t)\) est la population vectorielle totale.

•  \(\alpha\) est la vitesse de guérison des humains
•  \(\beta\) est la fréquence à laquelle les vecteurs piquent
•  \(q\) (ou \(q'\)) est la probabilité de transmission par piqûre du vecteur à l'humain (ou de l'humain au vecteur)
•  \(\lambda(t)\) est le nombre de nouveaux vecteurs adultes qui émergent par unité de temps. C'est une fonction périodique de période θ.
•  \(\mu\) est la mortalité des vecteurs.

Le premier terme dans la formule pour \(R_0\) est le même que pour le cas d'une population p constante de vecteurs mais avec p remplacé par la population vectorielle moyenne. La correction relative maximale due au second terme est \(\varepsilon^2/8\) et tend toujours à diminuer la reproductivité. Donc il est légèrement plus difficile pour une maladie à vecteurs d'envahir une population avec des fluctuations.

• une épidémie peut se développer si et seulement si \(R_0 > 1\)
• une épidémie peut être évitée si la population de vecteurs est uniformément divisée par la reproductivité tout au long de l'année.

4.2   L'épidémie de chikungunya à La Réunion

    La chikungunya est une maladie virale qui semble conduire à une immunité durable. Si de plus on veut prendre en compte la période d'incubation chez les humains et les vecteurs, le modèle suivant semble convenir: \begin{align} \frac{ds}{dt}&= \lambda(t) - \beta\, s(t)\, \frac{I(t)}{P} - \mu\, s(t),\tag{42}\\ \frac{de}{dt} &= \beta\, s(t)\, \frac{I(t)}{P} - (\gamma + \mu)\, e(t),\quad \frac{di}{dt} = \gamma\, e(t) -\mu\, i(t) ,\tag{43}\\ \frac{dS}{dt} &= -\beta\, i(t)\, \frac{S(t)}{P} \, ,\\ \frac{dE}{dt} &= \beta\, i(t)\, \frac{S(t)}{P} - \delta\, E(t)\, ,\quad \frac{dI}{dt} = \delta\, E(t) -\alpha\, I(t)\, ,\tag{44}\\ \frac{dR}{dt} &= \alpha\, I(t)\, .\tag{45} \end{align}

•  \(e(t)\) est la population de vecteurs infectée mais non infectieuse
•  \(E(t)\) est la population humaine infectée mais non infectieuse
•  \(1/\gamma\) est la période d'incubation moyenne chez les vecteurs
•  \(1/\delta\) est la période d'incubation moyenne chez les humains
•  \(R(t)\) est la population humaine immunisée.

    On utilise ce modèle pour essayer d'estimer la reproductivité pour l'épidémie de chikungunya de 2005 et 2006 à La Réunion. Comme les fluctuations de la population de vecteurs sont inconnues, on prend la forme simple \[p(t)=p_0 (1+\varepsilon\, \cos(\omega t - \phi)).\] Ce n'est pas trop déraisonnable quand on observe les courbes de température et de précipitations à La Réunion (figure 1b), les deux ayant un seul maximum annuel vers février et un minimum vers juillet. On a ainsi  \(\theta=\frac{2\pi}{\omega}=1\) an, et on peut prendre \(\phi=\frac{2\pi}{12}\). La fonction \(s(t)\) peut être éliminée du système (42)-(45) puisque  \(s(t)=p(t)-e(t)-i(t)\). Les autres valeurs des paramètres utilisées pour la simulation sont résumées dans le tableau 1. Noter par exemple que (chikungunya.net, #83) réfère à la question 83 dans la liste des questions souvent posées du site chikungunya.net. Ce site internet, rédigé par des épidémiologistes, est dédié à l'épidémie de chikungunya à La Réunion.

    On estime que l'incubation chez les humains dure entre 3 et 7 jours (Duhamel et coll., 2006, p. 6) ou entre 4 et 7 jours (chikungunya.net, #101). Mais d'après (#156), les humains peuvent commencer à être infectieux 2 ou 3 jours avant les symptômes. On a donc choisi 4 jours pour la période d'incubation. On estime que la période infectieuse après les symptômes chez les humains est d'environ 5 jours (Duhamel et coll., 2006, p. 7) ou entre 5 et 7 jours (#49,52). Vue la remarque précédente, on prend une valeur de 7 jours pour toute la période infectieuse.

    On estime que la période d'incubation chez les vecteurs est comprise entre 9 et 14 jours (chikungunya.net, #83), entre 4 et 5 jours (#253), ou entre une et deux semaines (#395). On a choisi 7 jours. Une fois infectés, il semblerait que les vecteurs le restent jusqu'à ce qu'ils meurent (#83). On estime que la durée de vie d'un vecteur adulte est comprise entre 4 et 10 semaines (#83) ou « plusieurs » semaines (#404). On a choisi un mois. Le vecteur peut piquer 5 ou 6 fois pendant sa vie (#404): on a choisi une moyenne d'une piqûre tous les 4 jours. On ignore si le vecteur infecté peut transmettre le virus à ses œufs (#83/385/442) : notre modèle ne prend pas en considération cette possibilité.

    L'infection chez les humains conduit à un état d'immunité (#10/385), qui dure probablement au moins plusieurs années puisque personne ne semble avoir souffert deux fois du chikungunya durant l'épidémie à La Réunion. Les cas asymptomatiques représentent entre 10 et 15% des cas d'après (#385) mais ne semblent pas inclus dans l'estimation du nombre de cas dans la figure 1; on n'en tient pas compte dans le modèle.

    Le premier cas de chikungunya à La Réunion a été détecté le 22 février 2005. Il a vraisemblablement été importé des Comores, où plusieurs milliers de personnes avaient déjà été infectées. En tenant compte de la période d'incubation et de la durée d'infection, on suppose pour la simulation qu'un humain dans le compartiment E s'introduit dans la population de La Réunion au début de la cinquième semaine de 2005. On poursuit la simulation du modèle jusqu'au début de février 2006, c'est-à-dire jusqu'à la mise en place d'un contrôle vectoriel de grande ampleur suite au pic élevé; ce contrôle n'est pas inclus dans le modèle. On suppose que le contrôle vectoriel avant cette date est négligeable dans le modèle.

     \(p_0\) et \(\varepsilon\) sont des paramètres inconnus qui doivent être estimés en utilisant la courbe épidémique (figure 1). On définit  \(p_{\max}=p_0 (1+\varepsilon)\) et \(p_{\min}=p_0 (1-\varepsilon)\). En utilisant une méthode rudimentaire par tâtonnements, on trouve un ajustement correct à la courbe épidémique, vue la simplicité du modèle, avec un nombre maximum de piqûres reçues par un humain par semaine égal à  \(\beta\, p_{\max}/P=\mbox{1,2}\) et un nombre minimum de piqûres par humain et par semaine égal à 6% de ce maximum, c'est-à-dire  \(p_{\min}/p_{\max}=6\%\) (figure 3). On tire de ceci  \(p_{\max}\), \(p_{\min}\), \(p_0=(p_{\max}+p_{\min})/2\) et  \(\varepsilon=(p_{\max}-p_{\min})/(p_{\max}+p_{\min})\). Numériquement, \(\varepsilon \simeq \mbox{0,887}\). On vérifie facilement que  \(\lambda(t)=dp/dt+\mu\, p(t)\) reste positif car  \(\varepsilon \leq 1/\sqrt{1+(\omega/\mu)^2}\).

    Maintenant que tous les paramètres de ce modèle sont fixés, on se tourne vers l'estimation de la reproductivité. En linéarisant les équations (43) et (44) près de l'équilibre sans maladie, on obtient \begin{align*} \frac{de_*}{dt} &= \beta\, p(t)\, \frac{I_*(t)}{P} - (\gamma + \mu)\, e_*(t),\quad \frac{di_*}{dt} = \gamma\, e_*(t) -\mu\, i_*(t) ,\\ \frac{dE_*}{dt} &= \beta\, i_*(t) - \delta\, E_*(t)\, ,\quad \frac{dI_*}{dt} = \delta\, E_*(t) -\alpha\, I_*(t)\, . \end{align*} Le noyau de l'opérateur de prochaine génération associé est \begin{equation} K(t,x)=\left (\begin{array}{cccc} 0 & 0 & 0 & \frac{\beta p(t)}{P}\, e^{-\alpha x}\\ \gamma\, e^{-(\gamma+\mu)x} & 0 & 0 & 0 \\ 0 & \beta\, e^{-\mu x} & 0 & 0\\ 0 & 0 & \delta\, e^{-\delta x} & 0 \end{array}\right )\, . \end{equation} Il est « cyclique » et de la forme particulière (7) avec \(f(t)=1+\varepsilon \cos (\omega t - \phi)\), tandis que les fonctions \(g_j(x)\) (\(1\leq j\leq 4\)) sont de la forme (10).  \(G(x)\) est donné par (11), \(\widehat{G}(x)\) par (14) et \(G_k\) par (20).

    Avec les valeurs numériques des paramètres comme ci-dessus, et avec n'importe laquelle des quatre méthodes de la section 3, on obtient \(R_0\simeq \mbox{3,4}\). Le programme peut être téléchargé à partir du site internet suivant

www.ummisco.ird.fr/perso/bacaer/chikungunya.sci.

    Répétons: la valeur numérique obtenue pour la reproductivité du chikungunya ne doit pas être prise trop au sérieux. Les valeurs des paramètres sont imprécises. L'hypothèse (2) est trop simple. On peut voir cela comme un exercice pour tester les différentes méthodes numériques, comme une source d'inspiration pour développer la théorie, ou comme une première tentative de modélisation en attendant des enquêtes de terrain concernant les fluctuations de la population d'Aedes albopictus.

5.   Remarques de conclusion

5.1   Autres applications

Modèles épidémiques avec  \(n=1\)

    Considérons un modèle épidémique avec un compartiment infecté et un noyau de la forme suivante \begin{equation}\tag{46} K(t,x)=[1+\varepsilon\, \cos(\omega t-\phi)]\, g(x). \end{equation} On a alors \(G(x)=g(x)\) comme déjà noté dans la section 2.  \(R_0\) peut être approximé par la formule (31). Le noyau (46) apparaît par exemple dans les modèles épidémiques SIS/SIR/SIRS avec un taux de contact sinusoïdal.

    Si la période infectieuse est distribuée exponentiellement comme dans (Dietz, 1976 ; Grossman et coll., 1977 ; Kuznetsov et Piccardi, 1994), on a alors \(G(x)=a\, e^{-b x}\). On vérifie facilement que \(G_0=a/b\) et que le coefficient de  \(\varepsilon^2\) dans (31) s'annule, de sorte que \(R_0\simeq a/b\). Avec la même définition de la reproductivité que celle de l'article présent, Bacaër et Guernaoui (2006, §5) ont démontré dans ce cas la formule exacte  \(R_0=a/b\). Bien sûr ce résultat a déjà été remarqué depuis longtemps, puisque le noyau (46) apparaît en connexion avec l'équation \[\frac{dI}{dt} = a (1+\varepsilon\, \cos(\omega t-\phi))\, I(t) - b\, I(t).\] On peut résoudre explicitement. On montre facilement que l'état d'équilibre nul est instable si et seulement si  \(a/b > 1\). Par analogie avec le cas trivial où ε=0, plusieurs auteurs ont posé  \(R_0=a/b\) comme définition. Ils ont remarqué que \(R_0\) était la moyenne temporelle de la fonction \(\mathcal{R}_0(t)= a (1+\varepsilon\, \cos(\omega t-\phi))/b\). Ils ont cru que cette propriété de moyennisation restait valable pour des modèles plus compliqués. Ce n'est pas le cas.

    Si la période infectieuse est une constante τ fixée comme dans (Cooke et Kaplan, 1976 ; Smith, 1977 ; Nussbaum, 1977 ; Nussbaum, 1978 ; Grossman, 1980), on a \[G(x)=a\quad \forall x < \tau,\quad \quad G(x)=0\quad \forall x > \tau.\] On a alors \(G_0=a\, \tau\), \(G_1=a \, \frac{1-e^{-i\omega \tau}}{i\omega}\), et (31) donne \begin{equation}\tag{47} R_0\simeq a\, \tau + \varepsilon^2\, \frac{2\, a\, \tau\, \sin^2(\omega \tau/2)}{[\omega \tau - \sin(\omega \tau)]^2 + [1-\cos(\omega \tau)]^2 } \Bigl [\frac{\omega \tau/2}{\tan(\omega \tau/2)}-1 \Bigr ] \, . \end{equation} Contrairement au cas du modèle pour le paludisme de la section 4.1, la saisonnalité peut augmenter ou diminuer la reproductivité. Cela dépend de la valeur numérique de ωτ. Noter que pour le cas exceptionnel où \(\omega=2\pi\) et \(a=1\) considéré par (Cooke et Kaplan, 1976 ; Smith, 1977 ; Nussbaum, 1977 ; Nussbaum, 1978), la formule (47) dit que  \(R_0=1+o(\varepsilon^2)\) si τ=1. On s'attend à avoir la formule exacte  \(R_0=1\) pour tout ε si τ=1, puisque (Smith, 1977 ; Nussbaum, 1977) ont montré que des solutions périodiques du modèle épidémique non linéaire complet existent si et seulement si \(\tau > 1\) .

Les modèles épidémiques avec  \(n=2\)

    Considérons un modèle épidémique avec deux compartiments infectés qui, après linéarisation près de l'équilibre sans maladie, est \[\frac{dI_1}{dt}\simeq -b_1\, I_1(t) + a_2\, [1+\varepsilon\, \cos (\omega t - \phi)]\, I_2(t),\quad \frac{dI_2}{dt} \simeq a_1\, I_1(t) - b_2\, I_2(t).\] Remarquer que le système (38) était de cette forme. Le noyau de l'opérateur de prochaine génération associé est \begin{equation}\tag{48} K(t,x)=\left (\begin{array}{cc} 0 & [1+\varepsilon\, \cos(\omega t-\phi)]\, a_2\, e^{-b_2\, x}\\ a_1\, e^{-b_1 x} & 0 \end{array}\right ). \end{equation} La formule (31) donne \begin{equation}\tag{49} R_0 \simeq \frac{a_1\, a_2}{b_1\, b_2} \Bigl (1 - \frac{b_1\, b_2}{\omega^2 + (b_1+b_2)^2} \, \frac{\varepsilon^2}{2} \Bigr )\, . \end{equation}

    Un exemple de ce type est le modèle pour le paludisme de (Anderson et May, 1991, p. 404). Les valeurs numériques utilisées dans cette référence sont: \(\omega=2\pi\), \(\varepsilon=15/25\), \(a_1=20\) par année, \(a_2=20\times 25\) par année, \(b_1=50\) par année et \(b_2=4\) par année. Les quatre méthodes numériques de la section 3, de même que la formule approchée (49), donnent \(R_0\simeq \mbox{49,4}\). Noter que le terme d'ordre le plus bas est \(\rho_0=50\).

    Un autre exemple est le modèle épidémique SEIR ou SEIRS avec un taux de contact sinusoïdal considéré par exemple dans (Schwartz et Smith, 1983 ; Aron et Schwartz, 1984 ; Kuznetsov et Piccardi, 1994 ; Altizer et coll., 2006, encadré 1 ; Ma et Ma, 2006, §4). Les valeurs numériques utilisées par (Ma et Ma, 2006, §4) sont: \(\omega=1\), \(\varepsilon=\mbox{0,8}\), \(a_1=\mbox{0,3}\), \(a_2=1\), \(b_1=\mbox{0,3}\), et  \(b_2=\mbox{0,99}\) (unités non spécifiées). Une simulation numérique a montré qu'aucune épidémie de peut s'établir dans ce cas. Mais avec  \(\varepsilon=0\), les auteurs ont remarqué que  \(\rho_0=(a_1\, a_2)/(b_1\, b_2)=1/\mbox{0,99} > 1\). La conclusion était que la moyennisation du taux de contact n'est pas la manière correcte de déterminer le seuil épidémique. En effet, les quatre méthodes numériques de la section 3 donnent  \(R_0\simeq \mbox{0,973} < 1\) si ε=0,8. La formule approchée (49) donne \(R_0\simeq \mbox{0,974}\).

    Un autre exemple est le modèle pour le choléra avec un taux de contact ou un taux de contamination de l'eau qui est sinusoïdal (Codeço, 2001). Cette référence considère aussi le cas où le coefficient \(b_2\), qui représente le taux de disparition de Vibrio cholerae dans l'eau, est une fonction sinusoïdale du temps. Le présent article ne fournit pas de formule approchée pour la reproductivité dans ce dernier cas, mais \(R_0\) peut toujours être calculé numériquement en utilisant par exemple la méthode de la section 3.4.

    On mentionne aussi la conjecture de (Moneim et Greenhalgh, 2005), qui suggère que la reproductivité (avec un seuil à 1) pour un modèle SEIRS avec une vaccination et un taux de contact périodiques se calcule en moyennant les coefficients périodiques. Cette référence de donne pas d'exemple numérique. Mais si l'on suppose que le taux de contact est constant et que la population saine dans la situation sans maladie est sinusoïdale, alors \(K(t,x)\) est exactement de la forme (48) et \(R_0\) est donné par (49). Si la moyennisation était correcte, le résultat ne devrait pas dépendre de ε. Donc la conjecture semble fausse.

5.3   Le cas stochastique

    Il serait utile pour l'épidémie de chikungunya à La Réunion d'avoir une estimation de la probabilité que l'épidémie s'éteigne à cause de l'hiver sachant la taille de la population humaine infectée au début de l'hiver. Pour répondre à cette question, on a évidemment besoin d'un modèle stochastique. Mais les modèles stochastiques pour les maladies à vecteurs avec saisonnalité sont difficiles à analyser. Dans cette section, on montre le lien qui existe entre la probabilité d'extinction au temps t et la reproductivité en utilisant un modèle épidémique très simple avec saisonnalité.

    Considérons le processus de naissance et de mort avec des coefficients \(a(t)\) et \(b(t)\) qui sont des fonctions périodiques de période θ \[\frac{dW_k}{dt} = a(t)\, (k-1)\, W_{k-1}(t) - [a(t)+b(t)]\, k\, W_k(t) + b(t)\, (k+1)\, W_{k+1}(t),\quad k\geq 1\] et \(dW_0/dt = b(t)\, W_1(t)\).  \(W_k(t)\) est la probabilité d'avoir k personnes infectées au temps t. Si Z personnes infectées sont introduites ou présentes au temps T, alors \[\,W_Z(T)=1,\quad \quad W_k(T)=0\quad \forall k\neq Z.\] La probabilité d'extinction au temps t se calcule en résolvant l'équation aux dérivées partielles du premier ordre vérifiée par la fonction génératrice \[g(t,x)=\sum_{k\geq 0} W_k(t) x^k.\] Le résultat, donné par (Bartlett, 1960), reste valide même si les coefficients ne sont pas périodiques: \[W_0(t)=\left [1-\frac{ e^{-\int_T^t (b(\tau)-a(\tau))\, d\tau}}{1+ \int_T^t a(\tau)\, e^{-\int_{\tau}^t (b(\sigma)-a(\sigma))\, d\sigma} d\tau}\right ]^Z . \] L'espérance du nombre de personnes infectées au temps t est donnée par \[I(t)=\sum_{k\geq 1} k\, W_k(t),\quad \frac{dI}{dt}=a(t)\, I(t)-b(t)\, I(t).\] Comme on peut le deviner avec cette équation différentielle, et comme le montre (Bacaër et Guernaoui, 2006, §5) pour des fonctions \(a(t)\) et \(b(t)\) qui sont périodiques, la reproductivité définie dans la section 2 est donnée par \[R_0=\frac{\int_0^\theta a(\tau)\, d\tau }{\int_0^\theta b(\tau)\, d\tau} \, .\] Remarquer que si \(R_0 < 1\), on a alors \[W_0(t)\mathop{\longrightarrow}_{t\to +\infty} 1.\] L'épidémie s'éteint. Si au contraire \(R_0 > 1\), on a alors \[W_0(t)\mathop{\longrightarrow}_{t\to +\infty} \Bigl [1 - 1/\int_T^\infty a(\tau)\, e^{\int_T^\tau (b(\sigma)-a(\sigma))\, d\sigma}\, d\tau\Bigr ]^Z.\] Il existe une certaine probabilité que l'épidémie persiste.

    Ainsi la reproductivité sert aussi de seuil entre deux situations :

• l'épidémie s'éteint avec une probabilité égale à 1 quel que soit le temps initial d'introduction du premier cas infecté
• l'épidémie s'éteint avec une probabilité strictement comprise entre 0 et 1 et dépendante du temps initial.

    Cette section évite l'introduction d'une reproductivité dépendante du temps,  \(R_0(t)\), définie par exemple pour le cas des maladies à vecteurs par la formule (1) avec p remplacé par p(t). Cette expression semble être un bon candidat pour discuter de l'invasion en fonction du temps d'introduction du pathogène. Mais l'exemple de (Hale, 1980, p. 121) mentionné dans (Diekmann et Heesterbeek, 2000, p. 149) suggère déjà que les cas suivants peuvent bien arriver simultanément :

•  \(R_0(t) < 1\) pour tout t
• l'équilibre sans maladie est instable :  \(R_0 > 1\) avec \(R_0\) défini comme dans l'article présent.

Calcul annexe

    En partant de la définition (9) de  \(G(x)\) et en supposant (10), on montre (11) par récurrence. Bien sûr, on ne perd pas en généralité à supposer que  \(a_j=1\ \forall\, j\). Pour n=2, un calcul simple montre que \[G(x) =\int_0^x e^{-\lambda_1\, x_1 -\lambda_2\, (x-x_1)}\, dx_1 =\frac{e^{-\lambda_1\, x}}{\lambda_2-\lambda_1} + \frac{e^{-\lambda_2\, x}}{\lambda_1-\lambda_2}\, .\] Supposons que (11) soit vrai pour un certain entier n. On a alors \begin{align*} G(x)&=\int_{\sigma_x^{n+1}} e^{-\lambda_1\, x_1 - \cdots - \lambda_n\, x_n - \lambda_{n+1}\, x_{n+1}}\, d\sigma_x^{n+1}\\ &=\int_0^x \Biggl ( \int_{\sigma_{x-x_{n+1}}^n}\!\!\!\!\!\! e^{-\lambda_1\, x_1 - \cdots - \lambda_n\, x_n}\, d\sigma_{x-x_{n+1}}^{n}\Biggr ) e^{-\lambda_{n+1}\, x_{n+1}}\, dx_{n+1}\\ &=\int_0^x \Biggl ( \sum_{j=1}^n \frac{e^{-\lambda_j\, (x-x_{n+1})}}{\prod_{\substack{k\neq j\\ k\leq n}} (\lambda_k - \lambda_j)} \Biggr ) e^{-\lambda_{n+1}\, x_{n+1}}\, dx_{n+1}\\ &=\sum_{j=1}^n \frac{e^{-\lambda_j\, x}}{\prod_{\substack{k\neq j\\ k\leq n}} (\lambda_k - \lambda_j)} \int_0^x e^{(\lambda_j-\lambda_{n+1}) x_{n+1}} dx_{n+1}\\ &=\sum_{j=1}^n \frac{e^{-\lambda_j\, x}}{\prod_{\begin{subarray}{l} k\neq j\\ k\leq n+1 \end{subarray}} (\lambda_k - \lambda_j)} + e^{-\lambda_{n+1} x} \sum_{j=1}^n \frac{1}{(\lambda_j-\lambda_{n+1}) \prod_{\substack{k\neq j\\ k\leq n}} (\lambda_k - \lambda_j)}\, . \end{align*} La deuxième somme de la dernière ligne est la décomposition en éléments simples de la fraction rationnelle suivante \[\frac{1}{\prod_{1\leq j \leq n} (\lambda_j-\lambda_{n+1})}\, .\] On a donc \[G(x)=\sum_{j=1}^{n+1} \frac{e^{-\lambda_j\, x}}{\prod_{\begin{subarray}{l} k\neq j\\ k\leq n+1 \end{subarray}} (\lambda_k - \lambda_j)},\] et la formule (11) est vraie pour \(n+1\).

Références bibliographiques