La reproductivité \(R_0\) dans les modèles d'activité sexuelle pour les épidémies de VIH/SIDA : exemple du Yunnan en Chine

Résumé

L'hétérogénéité dans les comportements sexuels joue un rôle important dans la propagation du VIH. Un modèle mathématique avec des équations différentielles ordinaires a été proposé en 1986 pour prendre en compte la distribution de l'activité sexuelle. On suppose un mélange proportionnel. Si M est la moyenne et V la variance de la distribution, alors la reproductivité qui fixe le seuil épidémique est proportionnelle à \(\,M+V/M\). On remarque ici que cette distribution théorique est différente de celle que l'on obtient dans les enquêtes de comportements au sujet du nombre de partenaires sexuels pendant une durée τ. Cette dernière est une loi mixte de Poisson dont la moyenne m et la variance v sont telles que \(M=m/\tau\) et \(V=(v-m)/\tau^2\). On a donc \(M+V/M=(m+v/m-1)/\tau\). De cette manière, on renforce le lien entre la théorie et les données dans les modèles d'activité sexuelle pour les épidémies de VIH/SIDA. Comme exemple, on considère les données concernant des travailleuses du sexe et leurs clients dans le Yunnan, en Chine. On trouve une borne supérieure pour la moyenne géometrique des probabilités de transmission dans ce contexte.

1.   Introduction

    En 2002, des études comportementales ont été menées sur huit cents hommes âgés de 18 à 50 ans et huit cents travailleuses du sexe dans le Yunnan et le Sichuan, deux provinces du sud-est de la Chine. Ces études faisaient partie d'un projet sino-britannique de prévention contre le VIH. Parmi de nombreuses autres questions, on a demandé aux hommes le nombre de travailleuses du sexe qu'ils avaient fréquentées au cours des douze derniers mois [11, Tableau 148-149]. On a demandé aussi aux travailleuses du sexe le nombre de clients qu'elles avaient eus pendant la semaine avant l'entretien [12, Tableau 78]. Le tableau 1 montre les résultats détaillés pour les 407 hommes du Yunnan. Les échantillons des différentes villes ont été pondérés selon la population de ces villes [11, Table 201]. Le tableau 1 ne montre donc pas des multiples entiers de la fraction 1/407. La première ligne du tableau 2 montre la moyenne et l'écart type, c'est-à-dire la racine carrée de la variance. Pour les 403 travailleuses du sexe du Yunnan qui ont participé à l'étude, seuls la moyenne, l'écart type, le minimum et le maximum ont été publiés (seconde ligne du tableau 2).

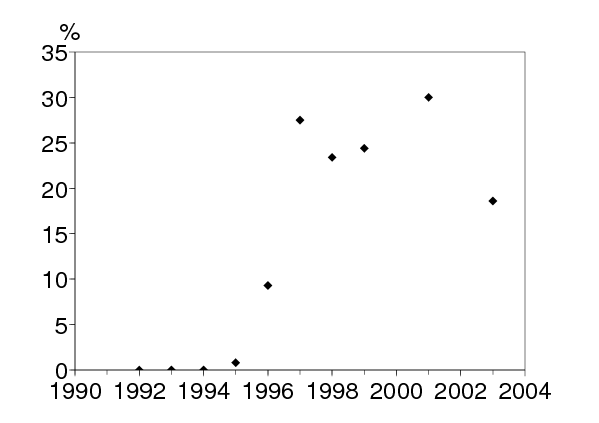
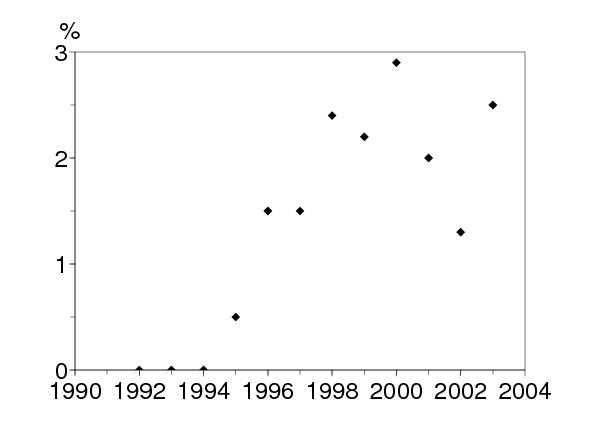
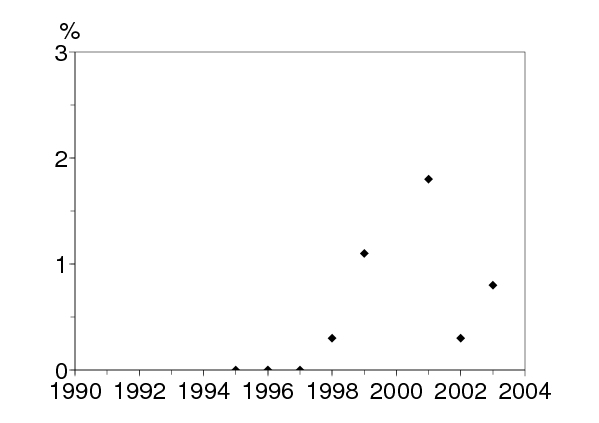
    À Kunming, la capitale de la province du Yunnan, l'épidémie de VIH est devenue importante parmi les usagers de drogue en 1996-1997 (figure 1a). Depuis, il semblerait que la prévalence du VIH dans ce groupe à risque se soit stabilisée entre 20% et 30%, un niveau probablement déterminé par le pourcentage des usagers de drogue qui partagent les seringues. La transmission sexuelle du VIH semble assez limitée lorsqu'on la compare à ce qui est arrivé il y a quelques années dans d'autres régions de l'Asie du sud-est telles que la Thaïlande. La prévalence du VIH est restée relativement faible parmi les travailleuses du sexe et leurs clients (figure 1b, c). Noter que le petit accroissement après 1996 est probablement dû au fait que certaines travailleuses du sexe et certains clients sont aussi des usagers de drogue. Mais il n'y a pas d'indication d'une croissance exponentielle de la transmission sexuelle. La situation dans d'autres parties du Yunnan a été résumée récemment [18].

    L'absence de croissance exponentielle de la prévalence du VIH parmi les travailleuses du sexe suggère que la reproductivité pour la transmission sexuelle du VIH entre les travailleuses du sexe et leurs clients reste inférieure à 1. C'est un peu surprenant. Est-il possible de comprendre cela avec les données sur les comportements sexuels?

    Dans cet article, on utilise un modèle mathématique pour les épidémies de VIH qui prend en compte la distribution de l'activité sexuelle. Les premiers modèles de ce type se focalisaient sur les hommes homosexuels et divisaient cette population suivant le nombre k de partenaires sexuels par an ([1, 2, 15] et [4, chapitre 11]). Le compartiment k était appelé le « groupe d'activité sexuelle k », k étant un nombre entier ≥0. Avec un mélange proportionnel, le seuil épidémique ne dépend pas seulement de la moyenne (notée M) mais aussi de la variance V de la distribution. Plus précisément, la reproductivité est proportionnelle à \(\,M+V/M\) et l'épidémie ne se produit que si \(R_0 > 1\). Pour une population homogène, la variance V est nulle et la reproductivité est simplement proportionnelle à l'activité sexuelle moyenne M. Ce modèle peut être modifié pour prendre en compte des distributions continues et non discrètes pour le taux d'acquisition de nouveaux partenaires sexuels [1, 2]. La reproductivité est alors toujours proportionnelle à \(M+V/M\,\) [6, p. 81].

    Le modèle a aussi été étendu aux populations hétérosexuelles ([15], [4, § 11.3.9]): si M et V sont la moyenne et la variance de l'activité sexuelle des hommes, si \(\,\widehat{M et \(\widehat{V sont la moyenne et la variance pour celle des femmes, alors la reproductivité est proportionnelle à \[\sqrt{(M+V/M) (\widehat{M}+\widehat{V}/\widehat{M})}\, .\] La variante avec des distributions continues et non discrètes pour le taux d'acquisition de nouveaux partenaires sexuels donne le même résultat pour la reproductivité [6, p. 83] (on peut remarquer dans cette référence que la formule pour la reproductivité est obtenue en considérant directement l'opérateur de prochaine génération, c'est-à-dire sans écrire explicitement les équations du modèle).

    A priori, il semblerait que la moyenne et la variance du tableau 2 puissent être utilisées directement dans la formule pour la reproductivité. Dans le présent article, on explique que ce n'est pas le cas. Supposons par exemple que le taux d'acquisition de nouveaux partenaires sexuels soit donné par une distribution continue. Les personnes dans le groupe d'activité sexuelle x ont un nouveau partenaire sexuel durant une durée infinitésimale dt avec une probabilité x×dt. x≥0 est un nombre réel. Donc si l'on demande aux personnes dans ce groupe combien de nouveaux partenaires elles ont eus pendant une durée τ avant l'entretien, on s'attend à ce que la réponse suive une distribution de Poisson de moyenne x×τ. Ainsi, la distribution dans la population du nombre de partenaires sexuels sur une période donnée est une « loi mixte de Poisson » [8, chapitre 2]. Des distributions de ce type sont utilisées par les compagnies d'assurance pour modéliser le nombre de demandes d'une certaine catégorie, par exemple celles enregistrées après un accident de la circulation ou après une maladie, au cours d'une période donnée [8, chapitre 9]). M est la moyenne, V  est la variance de la distribution de l'activité sexuelle, qui est une distribution de probabilité sur la demi-droite x≥0. \(m(\tau)\) est la moyenne, \(v(\tau)\,\) est la variance de la distribution du nombre de partenaires sexuels pendant une durée τ d'après une enquête comportementale. Cette distribution de probabilité est sur l'ensemble des nombre entiers ≥0. On peut montrer que \[M=m(\tau)/\tau,\quad V=(v(\tau)-m(\tau))/\tau^2.\] On a donc \begin{equation}\tag{1} M+\frac{V}{M}=\frac{1}{\tau} \Bigl (m(\tau)+\frac{v(\tau)}{m(\tau)}-1\Bigr )\, . \end{equation} En particulier, \(\,V\leq v(\tau)/\tau^2\). La variance dans l'enquête est toujours supérieure à la variance de la distribution de l'activité sexuelle.

    Pour une population homogène, par exemple, une population ne comprenant d'un seul groupe d'activité sexuelle x, la distribution rapportée serait une distribution de Poisson. Dans ce cas, \(\,v(\tau)=m(\tau)\). Alors le côté droit de (1) est égal à \(\,m(\tau)/\tau\) et la reproductivité est simplement proportionnelle à la moyenne rapportée du nombre de partenaires, comme on pourrait s'y attendre.

    Dans le cas \(\tau\to +\infty\), on a \(1/\tau \to 0\) et \[\frac{1}{\tau} \Bigl (m(\tau)+\frac{v(\tau)}{m(\tau)}-1\Bigr ) \simeq \frac{1}{\tau} \Bigl (m(\tau)+\frac{v(\tau)}{m(\tau)}\Bigr )\, .\] Donc le −1 dans (1) n'est important que quand τ est petit. Mais dans une enquête telle que celle faite dans le Yunnan, τ doit être petit parce que la personne que l'on interroge doit pouvoir se souvenir et compter tous ses partenaires sexuels pendant une durée τ. Cette question devient plus difficile à mesure que τ croît. Les concepteurs de l'enquête du Yunnan ont estimé que τ=1 an était une durée raisonnable pour les clients, de même que τ=1 semaine pour les travailleuses du sexe. C'est la méthode pratique pour résoudre une difficulté: estimer directement pour un client ou une travailleuse du sexe son groupe d'activité sexuelle x et construire la distribution d'activité sexuelle dans la population.

    Enfin, on peut remarquer qu'une expression semblable au côté droit de l'équation (1) se trouve dans la théorie des graphes aléatoires lorsqu'on étudie la plus grande composante connexe ([16] et [6, p. 170]).

    L'article est organisé de la manière suivante. Dans la section 2, on présente un modèle pour des hétérosexuels avec des équations différentielles ordinaires. L'activité sexuelle est une variable continue. Le modèle tient compte du renouvellement des hommes et des travailleuses du sexe car la durée moyenne de « travail » dans le Yunnan est 2,5 années [12, tableau 63]). Comme les données pour le Yunnan contiennent deux unités de temps, l'année pour les hommes et la semaine pour les travailleuses du sexe, un modèle avec une structure continue pour l'activité sexuelle est bien plus adapté qu'un modèle avec une structure discrète. On fait aussi attention à l'équilibre nécessaire entre le nombre de relations sexuelles comptées du point de vue des hommes avec celui du point de vue des travailleuses du sexe. On trouve la reproductivité pour le modèle par une méthode d'agrégation semblable à celle de [1, 2, 15] et de [4, chapitre 11]. Dans la section 3, on démontre la formule (1) et on l'utilise avec les données du tableau 2. De cette manière, on peut obtenir une borne supérieure pour la moyenne géometrique des probabilités de transmission dans le contexte de Kunming. Dans la section 4, on insiste sur la dépendance de la moyenne rapportée \(\,m(\tau)\) et de la variance rapportée \(v(\tau)\) par rapport à la durée τ sur laquelle les partenaires sexuels sont comptés. Notre analyse fait douter de la loi de puissance trouvée dans [3], qui relie \(\,m(\tau)\) et \(v(\tau)\). Cette loi est indépendante de τ. La conclusion résume les objectifs de l'article.

2.   Le modèle

    Les compartiments du modèle utilisé dans cet article sont les suivants, la variable x étant réelle et positive:

• \(S_0(t)\): nombre d'hommes sains au temps t qui n'ont jamais de relation avec des travailleuses du sexe;
• \(S(t,x)\): densité de clients sains au temps t qui appartiennent au « groupe d'activité sexuelle x ». La probabilité d'avoir un nouveau contact avec une travailleuse du sexe est x×dt pendant une durée infinitésimale dt.
• \(I(t,x)\) : densité de clients infectés dans le groupe d'activité sexuelle x ;
• \(\widehat{S}(t,x)\) : densité de travailleuses du sexe saines dans le groupe d'activité sexuelle x. La probabilité d'un nouveau contact avec un client est à x×dt pendant une durée infinitésimale dt.
• \(\widehat{I}(t,x)\) : densité de travailleuses du sexe infectées dans le groupe d'activité sexuelle x.

• \(A\), \(\widehat{A}(t)\) : nombre de nouveaux hommes et de nouvelles travailleuses du sexe entrant dans la population adulte par unité de temps; noter que l'arrivée de nouvelles travailleuses du sexe est supposée dépendre du temps;
• \(\varepsilon\) : fraction d'hommes qui n'ont jamais de contact avec des travailleuses du sexe (\(0 < \varepsilon < 1\))
• \(F(x)\), \(\widehat{F}(x)\) : densité de probabilité selon laquelle les hommes et les travailleuses du sexe entrent dans le groupe d'activité sexuelle x ; on suppose que \(\int_{0^+}^\infty F(x)\, dx=1-\varepsilon\) et que \(\int_0^\infty \widehat{F}(x)\, dx=1\). La distribution d'activité sexuelle des hommes adultes est donc composée d'une masse de Dirac en x=0 de masse ε, tandis que la fraction restante 1−ε est distribuée sur la demi-droite x>0. Toutes les travailleuses du sexe sont actives (x>0) par définition.
• \(B\), \(\widehat{B : probabilité de transmission du VIH par relation des femmes aux hommes et des hommes aux femmes; ce sont des moyennes qui ignorent l'hétérogénéité de la charge virale et la présence ou l'absence d'autres infections sexuellement transmissibles (ces deux aspects sont écartés dans le modèle parce que les données nécessaires ne sont pas disponibles); les personnes avec différents niveaux d'activité sexuelle pourraient aussi avoir différentes probabilités d'utiliser des préservatifs (\(B\) et \(\widehat{B}\,\) seraient alors aussi des fonctions de x) mais il y a peu d'information à ce sujet dans le rapport concernant le Yunnan [11, tableau 184];
• \(C\) : taux auquel les hommes adultes quittent la population en question à cause du vieillissement;
• \(\widehat{C : taux auquel les travailleuses du sexe arrêtent leur travail;
• \(D=\widehat{D : taux auquel les personnes infectées développement le SIDA; on suppose que les personnes avec le SIDA sortent de la population.

    Si l'on suppose aussi que \(\widehat{C} > C+D\), alors le système (5)-(7) avec \(\widehat{A}(t)\) défini par (10) est bien posé, et \(\widehat{A}(t)\geq 0\). Ceci veut dire que la rotation des travailleuses du sexe doit être assez rapide pour s'adapter aux variations de l'offre et de la demande causées par la mortalité du SIDA. On verra dans la pochaine section que les données pour le Yunnan vérifient la condition \(\,\widehat{C} > C+D\). Insistons sur les principales hypothèses du présent modèle:

• La durée des contacts n'est pas prise en compte. C'est l'hypothèse habituelle pour la modélisation des relations entre clients et travailleuses du sexe. Pour être plus précis, on considère les données sur la fréquence moyenne des contacts avec une travailleuse du sexe au cours des 30 derniers jours pour les hommes qui ont eu un contact au cours de l'année. Ce sont 21,4% de tous les hommes d'après le tableau 1 ci-dessus. La fréquence moyenne est 2,4 fois par mois [11, tableau 174]. Le nombre moyen de travailleuses du sexe rencontrées par les hommes est 1,0 par an (tableau 2 ci-dessus). On peut estimer le nombre moyen μ de travailleuses du sexe rencontrées au cours d'une année par les hommes actifs. On a \[\mbox{1,0}=0\times \mbox{78,6}\% + \mu \times \mbox{21,4}\%.\] On obtient \(\,\mu=\mbox{1,0}/\mbox{0,214}\simeq \mbox{4,67. Le nombre moyen de contacts pour ces clients sur un an s'estime en multipliant le nombre mensuel par le nombre de mois dans une année: \(\,\mbox{2,4}\times 12=\mbox{28,8. Donc on obtient une moyenne de \(\mbox{28,8}/\mbox{4,67}\simeq \mbox{6,2 contacts avec la même travailleuse du sexe et une durée moyenne du « contact » égale à \(\mbox{6,2}/\mbox{2,4}\simeq \mbox{2,6}\,\) mois (avec une moyenne de 2,4 « liaisons » par an). Cette échelle de temps est beaucoup plus courte que par exemple la durée moyenne de travail des travailleuses du sexe (\(1/C'=\)2,5 années d'après [12, tableau 63]). L'hypothèse initiale est donc quelque peu justifiée.
• On suppose que le mélange entre les groupes d'activité sexuelle est proportionnel car on n'a pas de meilleure information dans l'enquête.
• À mesure que l'épidémie se développe, on suppose que le recrutement des travailleuses du sexe s'adapte pour équilibrer l'offre et la demande. Il y a plusieurs autres possibilités. Par exemple, les hommes pourraient fréquenter les travailleuses du sexe moins souvent. Ces hypothèses n'entrent de toute façon pas dans le calcul de la reproductivité, qui est le point principal de cet article. Celui-ci ne dépend que du début de l'épidémie.

    L'état d'équilibre sans maladie du système (5)-(7) et (10) est donné par \begin{equation}\tag{13} S_*(x)=A\, F(x)/C, \quad \widehat{S}_*(x)=A\, M\, \widehat{F}(x)/(C\, \widehat{M}), \end{equation} \(I(x)=0\), \(\widehat{I}(x)=0\ \forall \, x > 0\). Linéarisons les équations (6) et (7) près de cet équilibre sans maladie et utilisons des lettres minuscules pour éviter toute confusion. On obtient \begin{align} \frac{\partial i}{\partial t}(t,x) &= B\, x\, S_*(x)\, \frac{\int_0^\infty y\, \widehat{i}(t,y)\, dy}{\int_0^\infty y\, \widehat{S}_*(y)\, dy} - (C+D)\, i(t,x) \tag{14}\\ \frac{\partial \widehat{i}}{\partial t}(t,x) &= \widehat{B}\, x\, \widehat{S}_*(x)\, \frac{\int_0^\infty y\, i(t,y)\, dy}{\int_0^\infty y\, S_*(y)\, dy} - (\widehat{C}+\widehat{D})\, \widehat{i}(t,x)\, . \tag{15} \end{align} Suivant la même méthode que celle de [4, § 11.3.9] pour un modèle avec une distribution discrète de l'activité sexuelle, on introduit les variables agrégées \[ J(t)=\int_0^\infty x\, i(t,x)\, dx,\quad \widehat{J}(t)=\int_0^\infty x\, \widehat{i}(t,x)\, dx\, . \] Il résulte de (14)-(15) que \begin{align*} &\frac{dJ}{dt}(t) = B \frac{\int_0^\infty x^2\, S_*(x)\, dx}{\int_0^\infty x\, \widehat{S}_*(x)\, dx}\, \widehat{J}(t) - (C+D)\, J(t)\\ &\frac{d\widehat{J}}{dt}(t) = \widehat{B} \frac{\int_0^\infty x^2\, \widehat{S}_*(x)\, dx}{\int_0^\infty x\, S_*(x)\, dx}\, J(t) - (\widehat{C}+\widehat{D})\, \widehat{J}(t) \, . \end{align*} Avec (2)-(3) et (13), ce système peut s'écrire \begin{align} &\frac{dJ}{dt}(t) = B\, \frac{V+M^2}{M}\, \widehat{J}(t) - (C+D)\, J(t)\tag{16}\\ &\frac{d\widehat{J}}{dt}(t) = \widehat{B}\, \frac{\widehat{V}+\widehat{M}^2}{\widehat{M}}\, J(t) - (\widehat{C}+\widehat{D})\, \widehat{J}(t)\, .\tag{17} \end{align} On peut alors facilement montrer que l'équilibre nul de ce dernier système est linéairement stable si et seulement si \begin{equation}\tag{18} R_0=\sqrt{\frac{B\, \widehat{B} (M+V/M) (\widehat{M}+\widehat{V}/\widehat{M}) }{(C+D)\, (\widehat{C}+\widehat{D})}} < 1\, . \end{equation} Commentons cette formule. On aurait pu arriver au même résultat en n'incluant pas dans le modèle les hommes qui n'ont jamais de contact avec les travailleuses du sexe, c'est-à-dire en restreignant notre attention aux clients des travailleuses du sexe. En effet, la distribution de l'activité sexuelle pour ces clients est \(\,\widetilde{F}(x)=F(x)/(1-\varepsilon)\) et l'activité sexuelle moyenne est \(\widetilde{M}=M/(1-\varepsilon)\). Noter que \(\widetilde{M} > M\). Mais si \(\,\widetilde{V est la variance correspondante, alors \[M+\frac{V}{M}=\frac{\int_0^\infty x^2 F(x)\, dx}{\int_0^\infty x\, F(x)\, dx} = \frac{\int_0^\infty x^2 \widetilde{F}(x)\, dx}{\int_0^\infty x\, \widetilde{F}(x)\, dx}=\widetilde{M}+\frac{\widetilde{V}}{\widetilde{M}}\, .\] Donc on obtient exactement le même \(R_0\).

3.   Lien avec les données

    Les personnes dans le groupe d'activité sexuelle x ont un nombre de partenaires sur une période de durée τ qui est distribué selon une loi de Poisson avec une moyenne x×τ [7, § XVII.2]. Donc leur probabilité d'avoir j partenaires sur une période de durée τ est \[e^{-x\tau}\, (x\tau)^j/j!\] Par conséquent, la fraction des hommes qui déclarent j partenaires sur une période de durée τ dans une enquête est \begin{equation}\tag{19} f_j(\tau)=\int_0^\infty e^{-x \tau}\, \frac{(x \tau)^j}{j!}\, dG(x) =\left \{\begin{array}{lll} \varepsilon + \int_{0^+}^\infty e^{-x \tau}\, F(x)\, dx & & j=0, \\ \int_0^\infty e^{-x \tau}\, \frac{(x \tau)^j}{j!}\, F(x)\, dx & & j\geq 1. \end{array}\right. \end{equation} Autrement dit, \((f_j(\tau))_{j\geq 0}\,\) est une loi mixte de Poisson [8, chapitre 2]. La moyenne rapportée \(\,m(\tau)\) et la variance \(v(\tau)\) sont données par \begin{equation}\tag{20} m(\tau)=\sum_{j\geq 1} j\, f_j(\tau)\, ,\quad v(\tau)=\sum_{j\geq 1} j^2\, f_j(\tau) - m(\tau)^2\, . \end{equation} Il résulte de (2), (19) et (20) que la moyenne rapportée \(m(\tau)=\tau M\) (voir aussi [8, proposition 2.1(i)]): \begin{equation}\tag{21} m(\tau) = \int_0^\infty \! e^{-x \tau} \sum_{j\geq 1} \frac{(x \tau)^j}{(j-1)!}\, dG(x) = \tau \int_0^\infty \! x\, dG(x) = \tau M\, . \end{equation} Par ailleurs, il résulte de (19) que \begin{equation}\tag{22} \sum_{j\geq 1} j (j-1) f_j(\tau) = \int_0^\infty e^{-x\tau} \sum_{j\geq 2} \frac{(x \tau)^j}{(j-2)!}\, dG(x)=\tau^2 \int_0^\infty x^2\, dG(x) \, . \end{equation} Combinons l'expression (3) de la variance V avec (20)-(21)-(22). On a \begin{align} V &=\frac{1}{\tau^2} \sum_{j\geq 1} j(j-1) f_j(\tau) - \Bigl (\frac{m(\tau)}{\tau}\Bigr )^2\nonumber\\ &= \frac{1}{\tau^2} \sum_{j\geq 1} j^2\, f_j(\tau) - \frac{1}{\tau^2} \sum_{j\geq 1} j\, f_j(\tau) - \frac{m(\tau)^2}{\tau^2}= \frac{v(\tau)-m(\tau)}{\tau^2} \, \tag{23} \end{align} (voir aussi [8, proposition 2.1(ii)]). Parce que \(\,m(\tau)\geq 0\) et \(V\geq 0\,\), toute loi mixte de Poisson a deux propriétés importantes:

• \(v(\tau)\geq m(\tau)\) (l'inégalité est stricte si \(V > 0\))
• \(v(\tau)\geq \tau^2\, V\) (l'inégalité est stricte si \(m(\tau) > 0\,\), c'est-à-dire si \(M > 0\)).

• Avec les expressions (2)-(3) pour M et V, on voit que la dimension physique (ou unité) de x est l'inverse d'un temps (\(T^{-1). L'unité de M est \(\,T^{-1. L'unité de V est \(\,T^{-2}\,\). L'unité de τ est \(\,T\). Mais m et v sont sans dimension (ce sont des nombres rapportés). On peut vérifier que les deux côtés de la formule (24) ont la même dimension.
• Dans le cas où \(\widehat{F}(x)\) est une distribution Gamma comme dans [1, 2], la distribution discrète associée est une loi binomiale négative \[\widehat{f}_j(\widehat{\tau})=\int_0^\infty e^{-x \widehat{\tau}}\, \frac{(x \widehat{\tau})^j}{j!}\, \widehat{F}(x)\, dx\, ,\] [8, p. 17]. Ce point, déjà noté dans [10], ne semble pas avoir été remarqué dans la littérature sur les modèles d'activité sexuelle pour le VIH/SIDA.

    Des problèmes proviennent cependant de l'incertitude concernant les probabilités de transmission par relation B et \(\,\widehat{B. On a estimé dans la section 2 qu'une relation dans le présent contexte signifie en moyenne 6 contacts sexuels. D'après une étude sur les travailleuses du sexe et leurs clients en Thaïlande [14], la probabilité de transmission par contact sexuel, de la femme à l'homme, peut atteindre 3%. C'est à cause de la prévalence des autres infections sexuellement transmissibles. D'autres études ont trouvé des probabilités de transmission par contact bien moindres, par exemple 0,11% pour des couples sérodiscordants en Ouganda [9]. Il est difficile de dire quelle estimation entre ces deux valeurs extrêmes conviendrait pour Kunming. En plus, l'utilisation de préservatifs est incluse en moyenne dans le paramètre B.

    Étant données toutes ces difficultés, on retourne la question de la manière suivante: sachant que l'on ne voit pas encore de croissance exponentielle de la transmission sexuelle du VIH, que peut-on en déduire pour les paramètres inconnus du modèle? Avec \(\,R_0 < 1\) et avec (18), (24) et (25), on obtient une borne supérieure pour la moyenne géometrique de ces probabilités de transmission : \begin{align*} \sqrt{B\, \widehat{B}}& < \sqrt{\frac{\tau\, \widehat{\tau}\, (C+D)\, (\widehat{C}+\widehat{D})}{(m+\frac{v}{m}-1) (\widehat{m}+\frac{\widehat{v}}{\widehat{m}}-1)}}\\ &=\sqrt{\frac{1 \times (7/365) \times (\mbox{0,4}+\mbox{0,1}) \times (1/32+\mbox{0,1})}{(\mbox{1,0}+\frac{\mbox{2,2}^2}{\mbox{1,0}}-1) (\mbox{3,0}+\frac{\mbox{4,1}^2}{\mbox{3,0}}-1)}} \simeq \mbox{0,58}\%\, . \end{align*} Avec l'hypothèse simplificatrice supplémentaire \(B=\widehat{B et en considérant (voir la section 2) qu'une relation représente en moyenne 6 contacts sexuels, on peut obtenir une borne supérieure pour la probabilité de transmission par contact sexuel : \(b < \mbox{0,1}\%\). En effet, \(\,1-(1-\mbox{0,1}\%)^6\simeq \mbox{0,6}\%\). Donc notre résultat est plus proche de l'estimation inférieure pour la probabilité de transmission par contact sexuel, mais ceci est peut-être dû au niveau élevé d'utilisation des préservatifs. Dans l'enquête comportementale de 2002 au Yunnan, 73,5% des clients ont déclaré avoir utilisé un préservatif lors de leur dernier rapport sexuel avec une travailleuse du sexe [11, tableau 177].

    Si l'on observait une croissance exponentielle de la transmission sexuelle, on pourrait estimer la moyenne géométrique \(\sqrt{B\, \widehat{B} parce que le taux de croissance \(\lambda\) du modèle est la plus grande valeur propre de la matrice du côté droit du système (16)-(17) \[\lambda=\frac{-(C+\widehat{C}+D+\widehat{D})+\sqrt{(C-\widehat{C})^2+4B\widehat{B} (M+V/M)(\widehat{M}+\widehat{V}/\widehat{M})}}{2}\, .\] Le temps de doublement est \(\,\log 2/\lambda\). Le point principal ici est que M et V ne peuvent être lus directement sur les données; on doit utiliser \(m(\tau)\) et \(v(\tau)\) avec le −1 additionnel dans les formules (24)-(25).

4.   Lien entre la moyenne et la variance

    Dans [3], on peut lire:

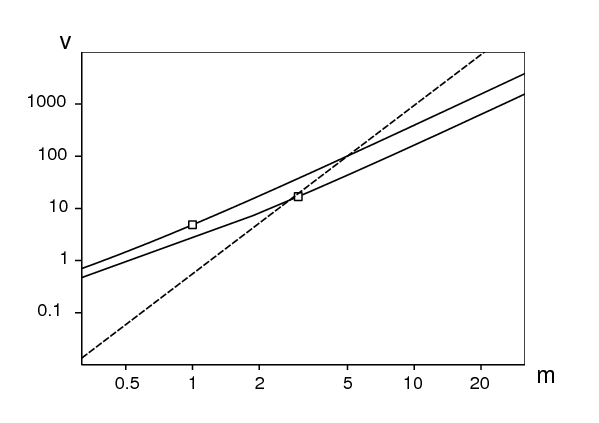
« a wide range of surveys of different populations employing different sampling methods and various time intervals for recall, reveal a remarkably consistent trend in the relationship between the mean and variance in the rate of acquisition of new partners. The summary statistics are related by a power law \(\,v=a\, m^b\,\), where a and b are constants. »

5.   Conclusion

    L'influence des modèles mathématiques a été analysée dans [17] de la manière suivante. L'auteur est vice-président de Futures Group. Cela peut expliquer pourquoi l'enquête menée au Yunnan et au Sichuan par Futures Group Europe rapporte à la fois la moyenne et la variance pour la distribution du nombre de partenaires sexuels :

The results of several modeling efforts, especially those of Roy Anderson and colleagues [...] have shown that the rate of partner change is one of the key factors influencing the speed and size of the epidemic [...] Although there is little evidence that this understanding has influenced program design to any great extent, it has certainly influenced research and evaluation efforts. Several of the key prevention indicators developed by GPA (Global Program on AIDS), UNAIDS, and USAID are designed to measure rates of partner change and concurrent partnerships. If these indicators are seriously applied, they will eventually influence program decisions by showing which interventions improve these indicators and which do not affect them.

• les paramètres théoriques \(\,(M,V)\)
• la moyenne \(m(\tau)\) et la variance \(v(\tau)\) pour une période de temps τ.

Remerciements

    Les auteurs ont reçu le soutien du Programme de Recherches Avancées de Coopérations Franco-Chinoises (PRA SI05-01, Modélisation de l'épidémie de VIH/SIDA dans les provinces du Yunnan et du Xinjiang).

Références bibliographiques