J. Math. Biol. 57 (2008) p. 649-673
Nicolas Bacaër
Institut de recherche pour le développement
32 avenue Henri Varagnat, 93143 Bondy, France
nicolas.bacaer@ird.fr
Xamxinur Abdurahman
Département de mathématiques et sciences des systèmes, Université du Xinjiang, Urumqi, Chine
Il y a eu de nombreuses études sur la résonance entre la période naturelle d'une maladie endémique et un taux de contact saisonnier périodique. Cet article ne se focalise pas sur la résonance pour des maladies endémiques mais sur la résonance pour des maladies émergentes. La périodicité peut avoir une grande influence sur le taux de croissance initial et donc sur le seuil épidémique. Il y a résonance quand l'équation d'Euler-Lotka a une racine complexe dont la partie imaginaire (c'est-à-dire la fréquence naturelle) est proche de la pulsation du taux de contact et dont la partie réelle n'est pas trop éloignée du paramètre malthusien. C'est une sorte d'analogue en temps continu des travaux de Tuljapurkar sur les modèles de population en temps discret. On illustre ce phénomène de résonance sur plusieurs modèles simples d'épidemies avec des contacts qui varient périodiquement de manière hebdomadaire. On explique les différences surprenantes entre un modèle SEIR périodique avec une période de latence distribuée exponentiellement et le même modèle avec une période de latence fixe.
Depuis au moins le travail de 1932 de Kermack et McKendrick, on sait que les maladies infectieuses peuvent présenter des oscillations amorties près d'un état d'équilibre endémique. En effet, en utilisant un modèle simple formé d'un système d'équations différentielles ordinaires, ils montrèrent que les valeurs propres de la matrice jacobienne en ce point d'équilibre peuvent être complexes. Ces valeurs propres déterminent une période naturelle d'oscillation. Depuis les années 1970 et en particulier depuis l'essor de la « théorie du chaos », de nombreux travaux ont montré que la résonance entre cette période naturelle et un taux de contact saisonnier périodique ou un autre facteur périodique pouvait induire un comportement dynamique inattendu.
Ceci se produit même pour des modèles mathématiques non linéaires très simples (Dietz, 1974 et 1976 ; Grossman et coll., 1977 ; Grossman, 1980 ; Smith, 1983a et 1983b ; Schwartz et Smith, 1983 ; Aron et Schwartz, 1984 ; Schwartz, 1985 ; Schaffer, 1985 ; Hethcote et Levin, 1989 ; Olsen et Schaffer, 1990 ; Rand et Wilson, 1991 ; Grenfell, 1992 ; Bolker et Grenfell, 1993 ; Kuznetsov et Piccardi, 1994 ; Grenfell et coll., 1995 ; Glendinning et Perry, 1997 ; Earn et coll., 2000 ; Keeling et coll., 2001 ; Keeling et Grenfell, 2002 ; Billings et Schwartz, 2002 ; Kamo et Sasaki, 2002 ; Dushoff et coll., 2004 ; Greenman et coll., 2004 ; Ireland et coll., 2004 ; Zeng et coll., 2005 ; Altizer et coll., 2006 ; Choisy et coll., 2006 ; Grassly et Fraser, 2006 ; Ireland et coll., 2007 ; Moneim, 2007a et 2007b).
Premièrement, si les équations linéarisées près de l'équilibre endémique ont une valeur propre complexe avec une partie imaginaire y proche de la pulsation ω du taux de contact et avec une partie réelle x proche de 0, alors des oscillations relativement petites du taux de contact peuvent causer de grandes oscillations de la prévalence. Deuxièmement, quand \(y/\omega\) est proche d'un nombre rationnel \(p/q\neq 1\) avec p et q petits, et pour des amplitudes d'oscillations suffisamment grandes du taux de contact, la prévalence peut osciller à une fréquence sous-harmonique. Du chaos peut également apparaître pour certaines plages des valeurs des paramètres. De cette manière, la théorie explique les séries temporelles pour l'incidence de certaines maladies telles que la rougeole, qui fut à une époque endémique mais avec des pics épidémiques à peu près tous les deux ans dans certaines villes (Soper, 1929), et dont on pensait par conséquent que la « période naturelle » d'oscillation près de son équilibre endémique était proche de deux ans. En écologie, il y a également des phénomènes de résonance similaires entre un environnement fluctuant et une période naturelle d'oscillation près d'un état d'équilibre non nul (Gurney et Nisbet, 1980 ; Nisbet et Gurney, 1982, chapitre 3).
D'après (Lotka, 1939a, p. 73 ; Lotka, 1939b), l'équation caractéristique (ou équation d'Euler-Lotka) pour les modèles démographiques linéaires en temps continu a aussi des racines complexes, qui provoquent des ondes de population. Lotka pensait qu'il y a toujours une infinité de telles racines et que l'une d'entre elle a en général une période naturelle associée proche d'une génération, soit deux ou trois décennies pour des populations humaines. A. J. Coale a étudié le cas d'une fertilité périodique et a remarqué un accroissement significatif du taux de croissance du modèle lorsque la période de la fertilité est proche d'une génération, un phénomène qu'il a aussi appelé résonance (Coale, 1972, figure 6.8). (Kim et Schoen, 1996 ; Schoen et Kim, 1997 ; Schoen, 2006) ont également étudié la résonance de l'amplitude des oscillations, mais pas la résonance du taux de croissance, dans les modèles linéaires en temps continu. (Tuljapurkar, 1985 et 1990), (Caswell, 2001, § 13.3.2) et (Keyfitz et Caswell, 2005, § 7.3.2) ont étudié la résonance dans les modèles matriciels linéaires en temps discret: étant donnée la transformation exponentielle qui relie les modèles en temps discret et ceux en temps continu, la résonance se produit quand la matrice qui décrit la croissance dans un environnement constant a une valeur propre complexe \(x+\mathrm{i}\, y\) avec \(\arctan(y/x)\) proche de ω et avec un module proche du rayon spectral de la matrice. À nouveau, (Tuljapurkar, 1985) se concentre sur la résonance de l'amplitude des oscillations mais pas sur la résonance du taux de croissance.
Les modèles mathématiques que l'on obtient par linéarisation de modèles épidémiques non linéaires près de l'équilibre sans maladie (et non l'équilibre endémique) sont très semblables aux modèles de population linéaires mentionnés dans le paragraphe précédent; la variable âge est remplacée par le temps écoulé depuis l'infection. Par conséquent, on s'attend à ce que la résonance du taux de croissance initial puisse aussi se produire dans un environnement périodique, ce qui change considérablement le seuil épidémique. Cela peut avoir des conséquences importantes pour les maladies émergentes. Noter cependant que pour beaucoup de maladies transmises par voie aérienne, le temps moyen entre deux générations d'infectés est de l'ordre d'une ou deux semaines; cela dépend de la période de latence. Ainsi la résonance n'est probable que si le taux de contact varie avec une période du même ordre de grandeur, typiquement s'il varie de manière hebdomadaire. Pour les enfants scolarisés, les contacts diminuent pendant les week-ends. On peut aussi imaginer une maladie infectieuse pour des animaux vendus une fois par semaine sur un marché.
La section 2 rappelle comment calculer le taux de croissance dans les modèles de population qui sont linéaires, périodiques et continus en temps. On donne une formule générale pour la perturbation du premier ordre; elle fait intervenir la notion de valeur reproductive dans un environnement périodique. Mais pour une petite perturbation périodique d'un modèle avec des coefficients qui ne dépendent pas du temps, cette formule montre qu'il est nécessaire d'inclure un terme de second ordre pour étudier la résonance du taux de croissance.
La section 3 présente trois méthodes différentes pour étudier la résonance. Les deux premières méthodes, l'une purement numérique, l'autre en partie analytique, reposent sur nos travaux antérieurs (Bacaër et Guernaoui, 2006 ; Bacaër, 2007 ; Bacaër et Ouifki, 2007). La troisième méthode suggère, comme on peut s'y attendre, que la résonance du taux de croissance se produit si
La section 4 applique les trois méthodes à cinq modèles épidémiques classiques avec des taux de contact périodiques pour montrer comment des modèles avec seulement de légères différences peuvent avoir des propriétés bien différentes:
En résumé, la règle a priori raisonnable d'un point de vue biologique, selon laquelle la résonance du seuil épidémique est importante lorsque la fréquence de l'environnement est proche d'une fréquence naturelle de la maladie, ne marche pas toujours. De manière surprenante, elle ne marche pas pour le modèles les plus simples, les modèles SIR et SEIR avec des période de latence et d'infectiosité distribuées exponentiellement. Cette règle doit être remplacée par une étude plus précise des racines complexes de l'équation d'Euler-Lotka. Un phénomène de résonance similaire peut se produire pour la reproductivité \(R_0\) (Bacaër et Ouifki, 2007, figure 1). On devrait donc revoir les estimations de la reproductivité pour les maladies se propageant dans un environnement périodique tel que l'école.
Le premier appendice contient une preuve de la croissance de la valeur reproductive totale d'une population dans un environnement périodique. Voir aussi (Michel et coll., 2005). C'est un corollaire de notre étude et une généralisation d'un résultat classique de R.A. Fisher pour les modèles de population autonomes (Fisher, 1930, chapitre 2). Le second appendice explique pourquoi la définition que l'on propose pour la valeur reproductive dans un environnement périodique semble avoir de meilleures propriétés que la définition utilisée par Ediev (2001, 2007).
Lorsqu'on étudie la stabilité de l'équilibre sans maladie d'un modèle épidémique, la première chose à faire est de linéariser le modèle près de cet équilibre. Le système linéaire qui en résulte peut en général s'écrire comme une équation intégrale de renouvellement \begin{equation}\tag{1} J(t)=\int_0^\infty \Phi(t,x)\, J(t-x)\, \mathrm{d}x\, . \end{equation}
Pour simplifier, on ne considérera que le cas \(n=1\) puisque c'est suffisant pour les exemples que nous avons à l'esprit. Ce cas intervient par exemple (mais pas seulement) lorsqu'on considère une population unique de personnes infectées avec
\(v(t,x)\) est la valeur reproductive d'un individu infecté depuis x unités de temps au temps t. Noter que dans les modèles démographiques, \(\beta(t,x)\) serait la fécondité et \(\mu(t,x)\) la mortalité. Sauf pour la normalisation, \(v(t,x)\) est la généralisation pour le modèle avec des coefficients périodiques de la définition de Fisher pour la valeur reproductive dans les modèles autonomes (Fisher, 1927 et 1930 ; Lotka et Fisher, 1927). Noter aussi que (Michel et coll., 2005) ne mentionne pas le lien avec la notion de valeur reproductive. (Grafen, 2006) a présenté récemment des généralisations dans d'autres directions.
Avec la présente définition de \(v(t,x)\,\), on peut facilement généraliser un théorème dû à Fisher (1930, chapitre 2) : \begin{equation}\tag{9} V(t)=\int_0^\infty \!\!\!i(t,x)\, v(t,x)\, \mathrm{d}x = V(0)\, e^{rt}\, , \end{equation} (voir l'appendice 1). C'est la raison principale pour laquelle la définition que nous utilisons pour la valeur reproductive dans un environnement périodique semble plus appropriée que celle de (Ediev, 2001 et 2007) (voir l'appendice 2).
Considérons d'abord le cas où \[\mu(t,x)=\mu_0(t,x)+\varepsilon\, \mu_1(t,x),\] avec deux fonctions \(\mu_0(t,x)\) et \(\mu_1(t,x)\) qui sont périodiques par rapport à \(t\). On écrit la première équation de (5) sous la forme \[\mathcal{L}_\varepsilon u=r \, u.\] \(\mathcal{L}_\varepsilon\) est un opérateur différentiel linéaire sur un espace de fonctions périodiques de période T (par rapport à la variable t) qui satisfont la contrainte donnée par la seconde équation de (5). Alors \[\mathcal{L}_\varepsilon=\mathcal{L}_0+\varepsilon\, \mathcal{M}, \quad (\mathcal{M}u)(t,x)=-\mu_1(t,x)\, u(t,x).\] \((r_0,u_0,v_0)\) est le triplet associé avec \(\mathcal{L}_0\). La théorie perturbative des opérateurs linéaires (Kato, 1984) dit que la valeur propre principale \(r_\varepsilon\) associée à \(\mathcal{L}_\varepsilon\) est donnée par \[r_\varepsilon= r_0+\varepsilon\, \rho+o(\varepsilon),\quad \varepsilon\to 0\] (notations de Landau), avec \begin{equation} \rho=\langle \mathcal{M}u_0,v_0\rangle = -\frac{1}{T}\int_0^T \!\!\!\int_0^\infty \!\!\!\mu_1(t,x)\, u_0(t,x)\, v_0(t,x)\, \mathrm{d}x\ \mathrm{d}t\, .\tag{10} \end{equation} Noter que \(\rho < 0\) si \(\mu_1 > 0\), comme il se doit.
De même, on peut considérer le cas où \[\beta(t,x)=\beta_0(t,x)+\varepsilon'\, \beta_1(t,x),\] avec deux fonctions \(\beta_0(t,x)\) et \(\beta_1(t,x)\) qui sont périodiques par rapport à t. Écrivons (7) \[\mathcal{L}'_\varepsilon v=r\, v, \quad \mathcal{L}'_\varepsilon=\mathcal{L}_0'+\varepsilon'\, \mathcal{N}, \quad (\mathcal{N}v)(t,x)=\beta_1(t,x)\, v(t,0).\] Noter que \((r_0,v_0,u_0)\) est le triplet associé à \(\mathcal{L}_0'\). La même théorie perturbative dit que la valeur propre principale \(r_\varepsilon\) associée à \(\mathcal{L}'_\varepsilon\) est donnée par \[r_\varepsilon= r_0+\varepsilon'\, \rho'+o(\varepsilon'), \quad \varepsilon'\to 0\] avec \begin{equation} \rho'=\langle \mathcal{N}v_0,u_0\rangle = \frac{1}{T}\int_0^T \!\!\! v_0(t,0) \int_0^\infty \!\!\!\beta_1(t,x)\, u_0(t,x)\, \mathrm{d}x\ \mathrm{d}t\, .\tag{11} \end{equation} Noter que \(\rho' > 0\) si \(\beta_1 > 0\), comme il se doit.
Coefficients indépendants du temps. Avec \(\mu(t,x)=\mu(x)\) et \(\beta(t,x)=\beta(x)\,\), (4) montre que le taux de croissance initial \(r\) est l'unique solution réelle de l'équation d'Euler-Lotka \begin{equation}\tag{12} 1=\int_0^\infty e^{-r\, x}\, \Phi(x)\, \mathrm{d}x\quad ,\quad \Phi(x)=\ell(x)\, \beta(x)\quad ,\quad \ell(x)=\exp\Bigl (-\int_0^x \mu(y)\, dy\Bigr ). \end{equation} Les solutions de (5)-(6) et (7)-(8) sont les formules bien connues dues à Lotka et Fisher pour la pyramide par âge et pour la valeur reproductive: \begin{align}\tag{13} u(x)&=\frac{e^{-r x}\, \ell(x)}{\int_0^\infty e^{-r y}\, \ell(y)\, dy}\, ,\quad v(x)= v(0) \int_x^\infty \!\!\!e^{-r (y-x)} \frac{\ell(y)}{\ell(x)}\, \beta(y)\, dy\, . \end{align} Avec \(\mu(x)=\mu_0(x)+\varepsilon \mu_1(x)\) ou \(\beta(x)=\beta_0(x)+\varepsilon'\, \beta_1(x)\,\), alors (10) et (11) deviennent \begin{equation} \rho=-\frac{\int_0^\infty \mu_1(x) \int_x^\infty e^{-r_0 y}\, \ell_0(y)\, \beta_0(y)\, dy\ \mathrm{d}x}{\int_0^\infty x\, e^{-r_0 x}\, \ell_0(x)\, \beta_0(x)\, \mathrm{d}x}\ ,\quad \rho'=\frac{\int_0^\infty e^{-r_0 x}\, \ell_0(x)\, \beta_1(x)\, \mathrm{d}x}{\int_0^\infty x\, e^{-r_0 x}\, \ell_0(x)\, \beta_0(x)\, \mathrm{d}x}\ . \end{equation} Aux notations près, ces formules sont dues à W.D. Hamilton (1966, équations (9) et (25)). Pour les modèles en temps discret, (Caswell, 2001 ; Demetrius, 1969 ; Goodman, 1971 ; Caswell, 1978) présentent des formules similaires.
Coefficients indépendants de x. Avec\(\,\mu(t,x)=\mu(t)\) et \(\beta(t,x)=\beta(t)\,\), on peut montrer, comme dans (Bacaër et Guernaoui, 2006, §5) pour r et \(u(t,x)\), que les solutions de (4), (5)-(6) et (7)-(8) sont \[ r=\frac{1}{T} \int_0^T\!\! (\beta(t)-\mu(t))\, \mathrm{d}t\ ,\] \[ u(t,x)=\frac{\beta(t-x)\ e^{-\int_{t-x}^t \beta(\tau)\, \mathrm{d}\tau}\ \psi(t)}{\frac{1}{T} \int_0^T\! \psi(\tau)\, \mathrm{d}\tau}\ ,\quad v(t,x)=\frac{\frac{1}{T} \int_0^T\!\! \psi(\tau)\, \mathrm{d}\tau}{\psi(t)}\ , \] avec \(\psi(t)=e^{-rt+\int_0^t (\beta(\tau)-\mu(\tau))\, \mathrm{d}\tau}\). Noter que la valeur reproductive \(v(t,x)\) est indépendante de x. Avec \(\mu(t)=\mu_0(t)+\varepsilon \mu_1(t)\) ou \(\beta(t)=\beta_0(t)+\varepsilon'\, \beta_1(t)\,\), alors (10) et (11) deviennent \[\rho=-\frac{1}{T} \int_0^T\!\! \mu_1(t)\, \mathrm{d}t\ ,\quad \rho'=\frac{1}{T} \int_0^T\!\! \beta_1(t)\, \mathrm{d}t\ ,\] comme il se doit avec l'expression de r.
Considérons maintenant le cas d'une petite perturbation périodique d'une situation autonome de la forme \begin{equation}\tag{14} \mu(t,x)=\mu_0(x)\, ,\quad \beta(t,x)=(1+\varepsilon \cos \omega t) \beta_0(x)\, \end{equation} avec \(|\varepsilon|\leq 1\). La sinusoïde est le facteur périodique le plus utilisé dans la littérature. Dans ce cas, l'équation (3) prend la forme \begin{equation}\tag{15} \Phi(t,x)=(1+\varepsilon \cos \omega t) \phi(x)\, , \end{equation} avec \(\phi(x)=\ell_0(x)\, \beta_0(x)\). Les fonctions \(u_0(t,x)\) et \(v_0(t,x)\) sont toujours indépendantes de t et données par (13). Parce que la moyenne temporelle de \(\beta_1(t,x)=\cos(\omega t) \beta_0(x)\) est 0, l'équation (11) donne \(\rho'=0\). Donc \(r_\varepsilon=r_0+o(\varepsilon)\). À cause de cela, on doit étudier le terme quadratique pour voir comment la résonance du taux de croissance peut se produire.
Il faut insister sur le fait que pas toutes les situations intéressantes sont de la forme (14). Par exemple, si l'on étudie l'influence d'un petit changement climatique sur une maladie à vecteurs, alors \(\mu_0(t,x)\) et \(\beta_0(t,x)\) seront des fonctions périodiques du temps à cause de la saisonnalité de la population de vecteurs. Dans un pareil cas, le changement du premier ordre dans le taux de croissance donné par l'équation (11) sera vraisemblablement différent de zéro.
Dans le reste de cet article (sauf dans les deux appendices), on se focalisera sur les modèles linéarisés qui s'écrivent sous la forme d'une équation de renouvellement (1) avec un noyau \(\Phi(t,x)\) de la forme (15), même si certains de ces modèles ne peuvent s'écrire sous la forme de l'équation aux dérivées partielles (2).
(Bacaër et Ouifki, 2007) a développé une méthode numérique spéciale pour calculer le taux de croissance \(r_\varepsilon\) lorsque le noyau \(\Phi(t,x)\) est de la forme (15). Noter cependant que les méthodes de (Bacaër, 2007 ; Bacaër et Ouifki, 2007) pouvaient gérer un facteur périodique arbitraire, en particulier le cas d'une fonction périodique en escalier. C'est plus réaliste non seulement pour la différence annuelle entre la période scolaire et les vacances, mais aussi pour la différence hebdomadaire entre les jours de la semaine et les week-ends.
On dira de manière peu précise qu'il y a « résonance » si \(r_\varepsilon\) est significativement plus grand que \(r_0\) si \(\varepsilon\neq 0\) pour certaines valeurs spéciales de la pulsation ω, c'est-à-dire si certaines fréquences spéciales favorisent la croissance. Les questions sont alors: la résonance peut-elle se produire et si oui, pour quelles valeurs des paramètres?
La première méthode, et la plus évidente, pour répondre à ces questions est de calculer \(r_\varepsilon\) numériquement et de le comparer avec \(r_0\). (Bacaër et Ouifki, 2007) a montré que le taux de croissance \(r_\varepsilon\) défini par (4) et (15) est la racine réelle la plus grande de l'équation suivante, qui fait intervenir une fraction continue, \begin{equation}\tag{16} 1/\widehat{\phi}_0(r)-1=2\, \mathrm{Re}\ \cfrac{\varepsilon^2/4}{1/\widehat{\phi}_1(r)-1-\cfrac{\varepsilon^2/4}{1/\widehat{\phi}_2(r)-1-\cfrac{\varepsilon^4/4}{\cdots}}}\ . \end{equation} \(\mathrm{Re}\) désigne la partie réelle. Par définition \begin{equation}\tag{17} \widehat{\phi}_n(r)=\int_0^\infty \phi(x)\, e^{-r\, x-n\mathrm{i}\omega x}\, \mathrm{d}x \end{equation} est la transformée de Laplace de \(\phi(x)\) calculée en \(z=r+n\mathrm{i}\omega\). Noter que lorsque \(\varepsilon=0\), (16) se réduit à \(\widehat{\phi}_0(r)=1\,\). C'est l'équation d'Euler-Lotka (12).
Il y a une deuxième méthode pour détecter la résonance. (Coale, 1972 ; Bacaër et Ouifki, 2007) ont obtenu une formule approchée du second ordre pour \(r_\varepsilon\) défini par (4) et (15) lorsque \(\varepsilon\) est petit: \begin{equation}\tag{18} r_\varepsilon = r_0 + \alpha\, \varepsilon^2 + o(\varepsilon^2) \quad ,\quad \alpha= -\frac{1}{2\, \widehat{\phi}'_0(r_0)}\, \mathrm{Re} \Big (\frac{1}{1/\widehat{\phi}_1(r_0)-1}\Bigr )\, . \end{equation} De cette manière, on voit que la résonance se produit si \(\alpha > 0\) et si \(\alpha\) n'est pas très petit comparé à \(r_0\). On peut facilement vérifier ces conditions numériquement. Pour les modèles avec un temps discret, Tuljapurkar (1985) a étudié la résonance de l'amplitude des oscillations de la population. Mais il n'a pas étudié la résonance pour le taux de croissance, après cependant avoir remarqué que \(r_\varepsilon=r_0+O(\varepsilon^2)\).
Il y a enfin une troisième méthode, peut-être la plus intéressante, pour détecter la résonance. Elle s'inspire des idées de (Tuljapurkar, 1985 et 1990) pour les modèles en temps discret mais aussi de l'abondante littérature mentionnée dans l'introduction sur la résonance près d'un équilibre endémique dans les modèles avec un temps continu. On s'attend à ce que la résonance se produise lorsque l'équation d' Euler-Lotka (12) a une paire de racines complexes conjuguées \(r=x\pm \mathrm{i} y\) avec y proche de ω et x proche du paramètre malthusien \(r_0\). En effet, si \(r=\xi+\mathrm{i} \omega\) est une racine exacte de (12), \[\widehat{\phi}_1(\xi)=\int_0^\infty \phi(x)\, e^{-\xi\, x -\mathrm{i} \omega x}\, \mathrm{d}x=1\, .\] Si la partie réelle ξ est proche de \(r_0\,\), plus précisément si \((r_0-\xi)/\omega\) est petit, on a très approximativement \[\widehat{\phi}_1(r_0)\simeq \widehat{\phi}_1(\xi)+(r_0-\xi) \widehat{\phi}_1'(\xi) = 1+(r_0-\xi) \widehat{\phi}_1'(\xi)\, .\] Remplaçons cette approximation dans la formule (18) pour α et considerons à nouveau que \(r_0-\xi\) est petit. On obtient \begin{equation}\tag{19} \alpha \simeq \frac{1}{2\, \widehat{\phi}_0'(r_0)\, (r_0-\xi)}\, \mathrm{Re} \Bigl (\frac{1}{\widehat{\phi}_1'(\xi)}\Bigr ) \, . \end{equation} Pour toute racine \(r=\xi+\mathrm{i} \omega\) de (12), on a \(\xi < r_0\). Noter aussi que \[\widehat{\phi}_0'(r_0)=-\int_0^\infty x\, \phi(x)\, e^{-r_0 x}\, \mathrm{d}x < 0\, .\] Par ailleurs, pour tout nombre complexe \(z=x+\mathrm{i} y\), on a \(\mathrm{Re}(1/z)=x/(x^2+y^2)\). Le signe de \(\mathrm{Re}(1/z)\) est le même que le signe de \(\mathrm{Re}(z)\). Donc pour (19), il suffit de déterminer le signe de \(\mathrm{Re}(\widehat{\phi}_1'(\xi))\). Le dénominateur \(r_0-\xi\) est petit. \(\alpha\) est positif si \[\mathrm{Re}(\widehat{\phi}_1'(\xi)) < 0.\] Autrement dit, \(r_\varepsilon\) sera significativement plus grand que \(r_0\) : il y a résonance. Le degré de résonance se mesure d'une certaine manière par la distance \(r_0-\xi\). Plus elle est petite, plus la résonance est importante. Rappelons aussi que \(r_0-\xi\) est lié à la vitesse avec laquelle la population converge vers sa forme stable (au sens de Lotka, avec la durée d'infection x qui remplace l'âge). Dans les modèles épidémiques, cette notion n'est pas très importante car les termes non linéaires dominent rapidement la dynamique.
On n'a pas réussi à démontrer que la condition \(\mathrm{Re}(\widehat{\phi}_1'(\xi)) < 0\) résultait de nos hypothèses. Donc pour le moment, elle doit être considérée comme une condition technique supplémentaire pour que la résonance se produise.
Pour cette troisième méthode, un point important est que l'équation d'Euler-Lotka peut ne pas avoir de racine complexe autre que la racine réelle, comme (Feller, 1941) l'a remarqué. C'est ce qui distingue les modèles où la résonance peut se produire et ceux où elle ne se produit pas. Bien qu'il soit possible de calculer le temps de génération moyen dans chaque modèle, cela ne veut pas dire qu'il y a toujours une racine complexe de l'équation d'Euler-Lotka avec une partie imaginaire proche de ce temps de génération. C'est ce que Lotka (1939a, p. 76-77) laissait croire.
Dans la prochaine section, on va étudier ces trois méthodes pour plusieurs modèles épidémiques simples avec un taux de contact périodique, pour montrer comment des modèles a priori peu différents peuvent avoir des propriétés bien différentes en ce qui concerne la résonance du taux de croissance initial.
On définit
L'état d'équilibre sans maladie est \((S,I,R)=(1,0,0)\). On linéarise le système près de cet état d'équilibre et l'on pose \(J(t)=a(t)\, I(t)\). C'est le nombre de nouvelles infections par unité de temps dans cette approximation. \(J(t)\) est solution d'une équation de la forme (1) avec (15). En utilisant (12), (17) et (18), on trouve facilement que \[\phi(x)=\bar{a}\, e^{-b\, x}\, ,\quad \widehat{\phi}_n(r)=\bar{a}/(b+r+n \mathrm{i} \omega)\, ,\quad r_0=\bar{a} - b\, ,\quad \alpha=0\, .\]
La première méthode pour détecter la résonance consiste à calculer \(r_\varepsilon\) numériquement. Pour le présent modèle, (Bacaër et Ouifki, 2007) a déjà remarqué que \(r=\bar{a} - b=r_0\) est une racine de (16) pour tout \(|\varepsilon|\leq 1\), mais a priori peut-être pas la plus grande. Donc on peut suspecter que \(r_\varepsilon=r_0\). Et en effet, une autre méthode, partant de la définition (4) de \(r_\varepsilon\), montre que \(r_\varepsilon=r_0\) (Bacaër et Guernaoui, 2006, §5). Il n'y a pas de résonance, quelles que soient les valeurs des paramètres.
La seconde méthode se focalise sur \(\alpha\). Ici α est nul, ce qui tend à confirmer qu'il n'y a pas de résonance. Quant à la troisième méthode, on note que \(r_0\) est la seule racine dans tout le plan complexe de l'équation d'Euler-Lotka (12). Donc il n'y a pas de résonance. Tout ceci est trivial car on arrive aux mêmes conclusions en calculant analytiquement la solution de l'équation différentielle linéarisée. C'est ce qui est fait d'habitude dans la littérature. Cependant il est tout de même intéressant de voir comment la méthode générale marche sur un exemple trivial.
L'indépendance de \(r_\varepsilon\) par rapport à \(\varepsilon\) dans ce modèle fait penser à l'idée que la distribution de probabilité \(\phi(x)/\int_0^\infty \phi(x)\, \mathrm{d}x=b\, e^{-bx}\) est, parmi les distributions de probabilité sur la demi-droite \([0,\infty)\) avec la même moyenne \(1/b\), celle d'entropie maximale et donc la plus « résistante aux perturbations environnementales », représentées ici par le facteur périodique (Demetrius, 1977). Demetrius (1977) insiste sur le lien entre l'entropie et les racines complexes de l'équation d'Euler-Lotka.
Considérons le modèle \begin{align*} S'(t)&= - a(t)\, S(t)\, I(t) \, ,\quad I'(t)\, =\, a(t)\, S(t)\, I(t) - a(t-\tau)\, S(t-\tau)\, I(t-\tau)\, ,\\ R'(t)&= a(t-\tau)\, S(t-\tau)\, I(t-\tau)\, , \end{align*} avec \(S+I+R=1\) et \(a(t)=\bar{a} (1+\varepsilon \cos \omega t)\). Le paramètre τ est la durée de la période infectieuse. Grossman (1980), Keeling et Grenfell (2002) ont étudié ce modèle avec des naissances et des morts. Cooke et Kaplan (1976), Smith (1977) et Nussbaum (1977,1978) l'ont étudié avec des personnes infectées qui retournent directement dans le compartiment sain. Cette dernière variante ne change pas le seuil épidémique.
L'état d'équilibre sans maladie est \((S,I,R)=(1,0,0)\). Le nombre de nouvelles infections par unité de temps dans le modèle linéarisé, \(J(t)=a(t)\, I(t)\,\), est solution d'une équation de la forme (1) avec (15). Ici \begin{equation}\tag{20} \phi(x)=\left \{\begin{array}{lll} \bar{a} & &\forall x < \tau,\\ 0 & & \forall x > \tau, \end{array}\right.\quad \quad \quad \widehat{\phi}_n(r)=\left\{\begin{array}{ll} \bar{a}\, \tau & \quad (r+n\mathrm{i}\omega=0)\\ \bar{a}\ \frac{1-e^{-r \tau -n \mathrm{i}\omega \tau}}{r+n \mathrm{i}\omega} & \quad (r+n\mathrm{i}\omega \neq 0) \end{array}\right.\, ,\quad \quad 1=\bar{a}\ \frac{1-e^{-r_0 \tau}}{r_0}\, . \end{equation} \(r_0\) est une fonction implicite de \(\tau\) \begin{equation}\tag{21} \tau=-\frac{1}{r_0} \log \Bigl (1-\frac{r_0}{\bar{a}}\Bigr )\, . \end{equation} De plus
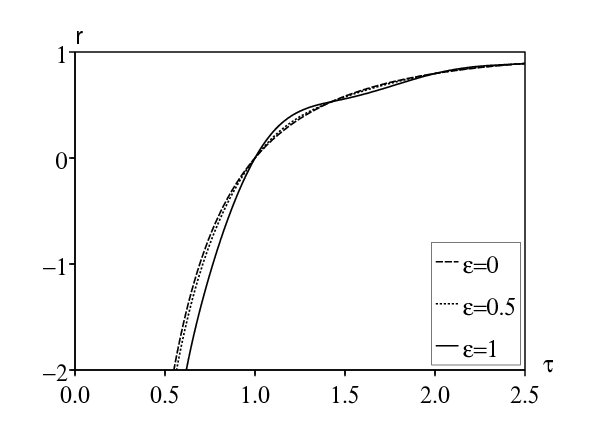
Avec la première méthode, la figure 1a montre comment le taux de croissance dépend de la période infectieuse τ. On a pris \(0 < \tau < \mbox{2,5}\) et diverses valeurs de \(\varepsilon\). Un zoom sur la figure montrerait que \(r_\varepsilon > r_0\) si \(\varepsilon\neq 0\) et \(1 < \tau < \mbox{1,43}\) ou alors \(2 < \tau < \mbox{2,44}\) (approximativement). Néanmoins la différence n'est pas significative. Il n'y a qu'une faible résonance.


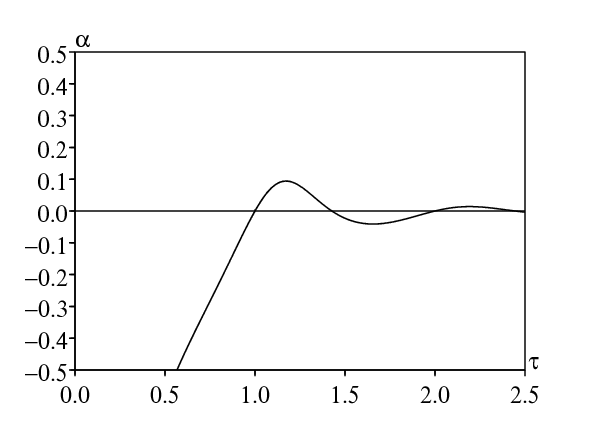
Avec la deuxième méthode, la figure 1b montre comment α dépend de la période infectieuse τ dans la même plage de valeurs. Numériquement, on a \(\alpha > 0\) si \(1 < \tau < \mbox{1,43}\) ou bien \(2 < \tau < \mbox{2,44}\), comme il se doit. Le maximum de \(\alpha/r_0\), qui est atteint lorsque \(\tau\simeq \mbox{1,174}\,\), est d'environ 9,4%. Cela confirme la faiblesse de la résonance.
Avec la troisième méthode, rappelons tout d'abord qu'il y a toujours une unique racine \(r_0\in \mathbb{R}\) de l'équation d'Euler-Lotka (20). Mais cette équation a aussi une infinité de paires de racines complexes conjuguées. C'est le cas plus généralement pour les modèles où \(\phi(x)\) a un support compact. Voir par exemple (Lopez, 1961, p. 15) ou (Gyllenberg, 1985, p. 323-324). Parmi ces racines complexes, certaines peuvent avoir une partie imaginaire égale à ω pour certaines valeurs particulières de τ. Pour trouver ces valeurs, noter que la dernière équation de (20), avec \(r=x+\mathrm{i} y\) à la place de \(r_0\), équivaut (si l'on exclut \(x=y=0\)) au système réel \[x=\bar{a} (1-e^{-x\tau} \cos(y\tau) )\ ,\quad y=\bar{a}\, e^{-x\tau}\, \sin(y\tau)\, .\] On prend \(y=\omega\) et on élimine x de la deuxième équation. On obtient une seule équation pour τ : \begin{equation}\tag{22} \frac{1}{\omega \tau} \log \Bigl [\frac{\omega}{\bar{a} \sin(\omega \tau)}\Bigr ] - \frac{1}{\tan(\omega\tau)} + \frac{\bar{a}}{\omega}=0\, . \end{equation} Le côté gauche
Avec \(\tau=\tau_1\,\), les racines complexes conjuguées de (20) avec la partie réelle la plus grande sont \(x_1\pm \mathrm{i} \omega\) avec \(x_1\simeq -\mbox{1,615}\,\), tandis que \(r_0\simeq \mbox{0,303}\). Donc bien que \(\ \mathrm{Re}(\widehat{\phi}_1'(x_1))\simeq -\mbox{1,19} < 0\) , la différence entre \(x_1\) et \(r_0\) est trop grande pour qu'une résonance significative se produise: \((r_0-x_1)/\omega \simeq \mbox{0,30}\). De même lorsque \( \tau=\tau_2\, \), les racines complexes conjuguées de (20) avec la seconde partie réelle la plus grande sont \(x_2\pm \mathrm{i} \omega\) avec \(x_2\simeq -\mbox{0,853}\,\), tandis que \(r_0\simeq \mbox{0,845}\). Donc bien que \(\ \mathrm{Re}(\widehat{\phi}_1'(x_2))\simeq -\mbox{2,23} < 0\,\), la différence entre \(x_2\) et \(r_0\) est à nouveau trop grande pour qu'une résonance significative se produise: \((r_0-x_2)/\omega \simeq \mbox{0,27}\). La même conclusion vaut pour les autres racines complexes avec une partie imaginaire égale à ω pour \(\tau=\tau_n\).
Supposons maintenant qu'il y ait une proportion \(E(t)\) de la population qui soit infectée mais pas encore infectieuse, c'est-à-dire qui soit dans la phase latente. Considérons le modèle \[ S'(t)=- a(t)\, S\, I\, ,\quad E'(t)=a(t)\, S\, I -c\, E,\quad I'(t)=c\, E - b\, I\, ,\quad R'(t)=b\, I\, , \] avec \(S+E+I+R=1\) et \(a(t)=\bar{a} (1+\varepsilon \cos \omega t)\). Le nouveau paramètre c est le taux auquel les personnes infectées deviennent infectieuses. (Dietz, 1976 ; Schwartz et Smith, 1983 ; Aron et Schwartz, 1984 ; Schwartz, 1985 ; Rand et Wilson, 1991 ; Grenfell, 1992 ; Bolker et Grenfell, 1993 ; Kuznetsov et Piccardi, 1994 ; Grenfell et coll., 1995 ; Keeling et Grenfell, 2002 ; Billings et Schwartz, 2002 ; Altizer et coll., 2006 ; Moneim, 2007a et 2007b) ont étudié ce modèle avec en plus des naissances et des morts, (Ma et Ma, 2006) avec les personnes guéries qui retournent dans le compartiment sains, et (Greenman et Norman, 2007) avec les deux. Ce modèle converge vers le modèle SIR de la section 4.1 si \(c\to +\infty\,\).
L'état d'équilibre sans maladie est \((S,E,I,R)=(1,0,0,0)\). Le nombre de nouvelles infections par unité de temps dans le modèle linéarisé, \(J(t)=a(t)\, I(t)\,\), est solution d'une équation de la forme (1) avec (15). Ici, \[\phi(x)=\bar{a}\, c \ \frac{e^{-c\, x}-e^{-b\, x}}{b-c}\, ,\quad \widehat{\phi}_n(r)=\frac{\bar{a}\, c}{(r+c+n\mathrm{i}\omega) (r+b+n\mathrm{i}\omega)}\, , \] \begin{equation}\tag{23} r_0=\frac{-(b+c)+\sqrt{(b-c)^2+4\bar{a}c}}{2}\, ,\quad \alpha= \frac{-(\bar{a}\, c)^2}{\sqrt{(b-c)^2+4\bar{a}c}\ [\omega^2+(b-c)^2+4\bar{a}\, c]}\, . \end{equation}
Pour la première méthode, considérons par exemple le cas où \(T=2\pi/\omega=1\) semaine, qui modélise des différences de taux de contact entre les jours de la semaine et les week-ends, et où la période infectieuse moyenne \(1/b\) est égale à 2 jours, soit 2/7 semaine. Prenons un taux de contact moyen \(\bar{a}=\mbox{1,2}\, b\), ce qui donne une reproductivité \(\bar{a}/b=\mbox{1,2}\) si \(\varepsilon=0\). C'est une hypothèse raisonnable si l'on considère une maladie émergente. La figure 2 montre comment le taux de croissance dépend de la période de latence moyenne pour diverses valeurs de \(\varepsilon\). Noter que \(r_\varepsilon\) est toujours plus petit que \(r_0\) si \(\varepsilon\neq 0\). Il n'y a pas de résonance.
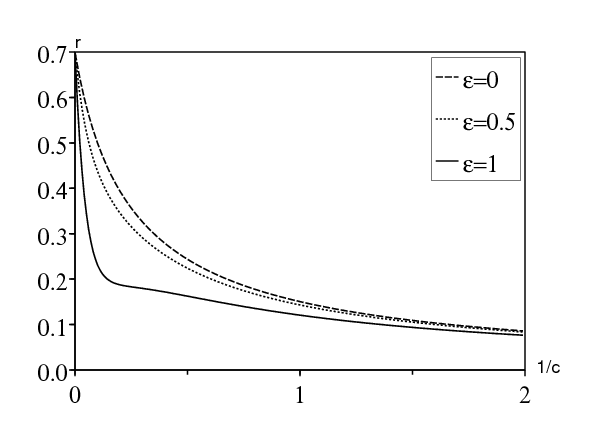
Pour la deuxième méthode, on remarque que \(\alpha < 0\) : il n'y a pas de résonance. Quant à la troisième méthode, l'équation d'Euler-Lotka (12) pour ce modèle n'a qu'une seule racine, à savoir \(r_0\,\), dans la partie du plan complexe où converge l'intégrale du côté droit de (12): \(\mathrm{Re}(r) > \max\{-b,-c\}\). Noter que \(r_0\) est solution d'une équation pôlynomiale de degré 2. L'autre solution, donnée par (23) avec un signe moins devant la racine carrée, est une racine de l'équation déduite de (12) par continuation analytique de l'intégrale (Feller, 1941). Pour cette seconde solution, l'intégrale diverge. De toute façon, cette solution est réelle; il n'y a pas de résonance.
Le modèle est donné par \begin{align*} S'(t)&= - a(t)\, S(t)\, I(t) \, ,\quad E'(t)\, =\, a(t)\, S(t)\, I(t) - a(t-\tau)\, S(t-\tau)\, I(t-\tau)\, ,\\ I'(t)&=a(t-\tau)\, S(t-\tau)\, I(t-\tau) - b\, I(t)\, ,\quad R'(t)\, =\, b\, I(t)\, , \end{align*} avec \(S+E+I+R=1\) et \(a(t)=\bar{a} (1+\varepsilon \cos \omega t)\). Il figure implicitement dans (Williams et Dye, 1997) et sous une forme légèrement différente dans (Bacaër et Ouifki, 2007). Le paramètre τ est maintenant la durée de la période de latence. Le modèle converge vers celui de la section 4.1 si \(\tau\to 0\).
L'état d'équilibre sans maladie est \((S,E,I,R)=(1,0,0,0)\). Le nombre de nouvelles infections par unité de temps dans le modèle linéarisé, \(J(t)=a(t)\, I(t)\,\), est solution d'une équation de la forme (1) avec (15). Ici \begin{equation}\tag{24} \phi(x)=\left\{\begin{array}{lll} 0 & & \forall x < \tau,\\ \bar{a}\, e^{-b(x-\tau)} & & \forall x > \tau, \end{array}\right. \quad \quad \widehat{\phi}_n(r)= \bar{a}\, \frac{e^{-n\mathrm{i} \omega \tau - r\tau}}{r+b+n\mathrm{i} \omega}\, ,\quad \quad r_0 = \bar{a} \, e^{-r_0 \tau} - b\, . \end{equation} Noter à nouveau que la formule pour \(r_0\) n'est pas explicite. La formule (18) pour α ne peut être vraiment simplifiée.
Pour la première méthode, on a choisi comme dans la section précédente \(T=2\pi/\omega=1\) semaine, \(1/b=2\) jours ou 2/7 semaine, et \(\bar{a}=\mbox{1,2}\, b\). La figure 3a montre comment le taux de croissance dépend de la période de latence pour diverses valeurs de ε. Remarquer dans la figure 3a que la résonance se produit approximativement si \(\mbox{0,66} < \tau < 1\) ou bien \(\mbox{1,66} < \tau < 2\). Il y a aussi résonance pour des valeurs plus grandes de τ, que l'on ne montre pas. (Bacaër et Ouifki, 2007) a obtenu un résultat semblable pour un modèle légèrement différent (SEIS et non SEIR); mais aucune explication pour les bosses n'avait été donnée. Noter que lorsque \(\varepsilon=1\), le taux de croissance \(r_\varepsilon\) peut devenir négatif dans une certaine plage de valeurs de la période de latence. La moyennisation du taux de contact (ce qui équivaut à prendre \(\varepsilon=0\)) prédirait une croissance épidémique alors qu'en fait aucune épidémie ne peut envahir la population.
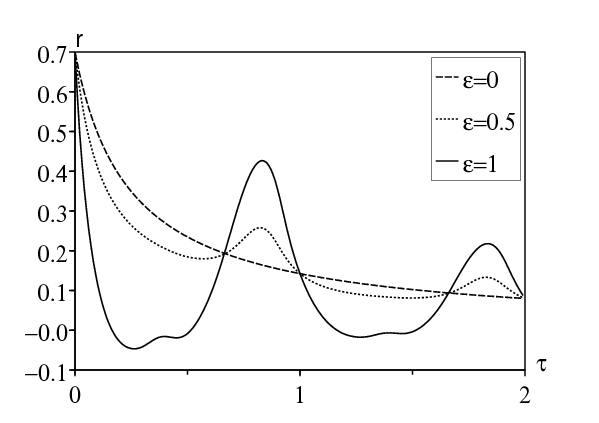
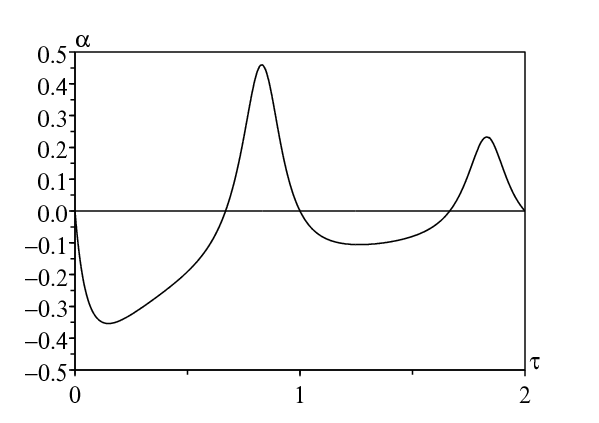
Avec la deuxième méthode, on peut vérifier numériquement que \(\alpha > 0\) au moins pour \(\mbox{0,66} < \tau < 1\) et \(\mbox{1,66} < \tau < 2\) (Figure 3b). Avec la troisième méthode, la question est de savoir si l'équation d'Euler-Lotka du côté droit de (24) peut avoir des solutions r avec une partie imaginaire y égale à ω. Avec \(r=x+\mathrm{i} y\,\), l'équation pour r peut s'écrire comme un système réel pour x et y : \[x = \bar{a} \, e^{-x \tau} \cos(y \tau) - b\, ,\quad y = - \bar{a} \, e^{-x \tau} \sin(y \tau) \, . \] Avec \(y= \omega\,\), on élimine x de la seconde équation. On obtient \begin{equation}\tag{25} \frac{1}{\omega \tau} \log \Bigl [- \frac{\omega}{\bar{a}\, \sin(\omega \tau)} \Bigr ] - \frac{1}{\tan(\omega\tau)} -\frac{b}{\omega}=0\, . \end{equation} Comme dans la section 4.2, le côté gauche est une fonction continue de τ pour tout \((n-1/2)T < \tau < n T\) et tout entier \(n\geq 1\), qui converge vers −∞ si \(\tau\to (n-1/2)T^+\,\), et qui converge vers +∞ si \(\tau\to nT^-\). Donc (25) a une infinité de solutions \(\tau_{1} < \tau_{2} < \cdots\) qui convergent vers +∞, pour lesquelles on peut s'attendre à de la résonance. Résolvons (25) numériquement avec les mêmes valeurs des paramètres que ci-dessus. On obtient: \(\tau_{1}\simeq \mbox{0,819}\), \(\tau_{2}\simeq \mbox{1,825}\), \(\tau_3\simeq \mbox{2,827}\ldots\)
Avec \(\tau=\tau_1\,\), les racines complexes conjuguées de (24) avec la partie réelle la plus grande sont \(x_1\pm \mathrm{i} \omega\) avec \(x_1\simeq -\mbox{0,609}\,\), tandis que \(r_0\simeq \mbox{0,166}\). On a \(\ \mathrm{Re}(\widehat{\phi}_1'(x_1))\simeq -\mbox{0,88} < 0\). La différence entre \(x_1\) et \(r_0\) est assez petite: \((r_0-x_1)/\omega\simeq \mbox{0,12}\). Donc il y a résonance si \(\tau\simeq \tau_1\). Avec \(\tau=\tau_2\,\), les racines complexes de (24), avec la partie réelle qui arrive en second par ordre décroissant, sont \(x_2\pm \mathrm{i} \omega\) avec \(x_2\simeq -\mbox{0,284}\,\), tandis que \(r_0\simeq \mbox{0,086}\). À nouveau, \(\ \mathrm{Re}(\widehat{\phi}_1'(x_2))\simeq -\mbox{1,89} < 0\). La différence entre \(x_2\) et \(r_0\) est petite: \((r_0-x_2)/\omega\simeq \mbox{0,06}\). Il y a résonance lorsque \(\tau\simeq \tau_2\). Il y a aussi résonance lorsque \(\tau=\tau_n\) et \(n > 2\).
D'un point de vue pratique, il n'est pas impossible qu'une maladie ait une période de latence proche de \(\tau_{1}\) (ici, environ 5,7 jours) suivie en moyenne de deux jours de période infectieuse. Un taux de contact avec une périodicité d'une semaine (due à la différence entre les jours de la semaine et les week-ends) peut provoquer une forte résonance pour une telle maladie. Noter ici que le temps entre deux générations (\(\int_0^\infty x\, \phi(x)\, \mathrm{d}x/\int_0^\infty \phi(x)\, \mathrm{d}x=\tau_1+1/b\simeq \mbox{7,7}\) jours) est proche de la périodicité du taux de contact, \(T=7\) jours . Mais cette règle approchée pour la résonance ne fonctionnait pas pour le modèle de la section précédente. La différence entre la figure 2 et la figure 3a est un peu surprenante. Il s'agit de modèles SEIR, le premier avec une période de latence distribuée exponentiellement, le second avec une période de latence fixe. La conclusion biologique, savoir si la maladie va s'intaller ou pas, semble très dépendant du choix entre ces deux modèles a priori similaires. Des modèles avec de petites différences peuvent donc se comporter très différemment quant à la résonance du taux de croissance initial.
Les modèles SEIR où la période de latence et la période infectieuse sont fixes, tels que ceux avec en plus des naissances et des morts (Grossman, 1980 ; Keeling et Grenfell, 2002), présentent une résonance similaire du taux de croissance initial. Il est encore possible de trouver des valeurs des paramètres pour lesquelles il y a une racine complexe de l'équation d'Euler-Lotka avec une partie imaginaire y égale à ω. Mais l'astuce qui consiste à éliminer la partie réelle x pour obtenir une seule équation comme dans (25) ne fonctionne plus.
Pour comprendre pourquoi les modèles des deux dernières sections donnent des résultats si différents, considérons le cas d'une période de latence qui suit la loi Gamma. C'est une généralisation à la fois de la distribution exponentielle et de la distribution de Dirac lorsque la période de latence est fixe. Plus précisément, \[f(x)=c^\nu\, x^{\nu-1}\, e^{-c\, x} / \Gamma(\nu)\] est la distribution de la période de latence, où \(c > 0\) et \(\nu\geq 1\) sont des nombres réels. La période de latence moyenne est \(\tau=\nu/c\) et la variance est \(\sigma^2=\nu/c^2\). Si ν=1, on retrouve la distribution exponentielle avec une moyenne égale à \(1/c\) de la section 4.3. La distribution Gamma converge vers la distribution de Dirac en \(x=\tau\), comme dans la section 4.4, si \(\nu\) et \(c\) convergent vers +∞ tandis que le quotient \(\nu/c\) est maintenu constant et égal à \(\tau\).
Le modèle est \begin{align*} S'(t)&= - a(t)\, S(t)\, I(t)\, ,\\ E(t,0)\, &=\, a(t)\, S(t)\, I(t)\, , \quad \frac{\partial E}{\partial t}+\frac{\partial E}{\partial x}\, =\, -\gamma(x)\, E(t,x)\, ,\\ I'(t)&=\int_0^\infty \gamma(x)\, E(t,x)\, \mathrm{d}x - b\, I(t)\, ,\\ R'(t)\, &=\, b\, I(t)\, , \end{align*} avec \(S(t)+\int_0^\infty E(t,x)\, \mathrm{d}x + I(t)+R(t)=1\) et \(a(t)=\bar{a} (1+\varepsilon \cos \omega t)\). Ici, \(\gamma(x)\) est lié à \(f(x)\) par la relation \[e^{-\int_0^x \gamma(y)\, \mathrm{d}y}=1-\int_0^x f(y)\, \mathrm{d}y,\] c'est-à-dire \[\gamma(x)=f(x)/(1-\int_0^x f(y)\, \mathrm{d}y).\] (Dietz, 1976 ; Keeling et Grenfell, 2002) ont étudié des variantes de ces modèles. Ici on peut montrer que le nombre de nouvelles infections par unité de temps dans le modèle linéarisé \(J(t)=a(t)\, I(t)\) est solution d'une équation de la forme (1) avec (15) et \[\phi(x)=\bar{a} \int_0^\infty e^{-b(x-y)}\, f(y)\, \mathrm{d}y\, .\] On peut aussi montrer que \[\widehat{\phi}_n(r)=\frac{\bar{a}\, c^\nu}{(b+r+n\mathrm{i} \omega) (c+r+n\mathrm{i} \omega)^\nu}\, ,\quad r_0 = \frac{\bar{a}\, c^\nu}{(c+r_0)^\nu}-b\, . \] Noter à nouveau que la formule pour \(r_0\) n'est pas explicite. La formule (18) pour α ne peut être simplifiée.
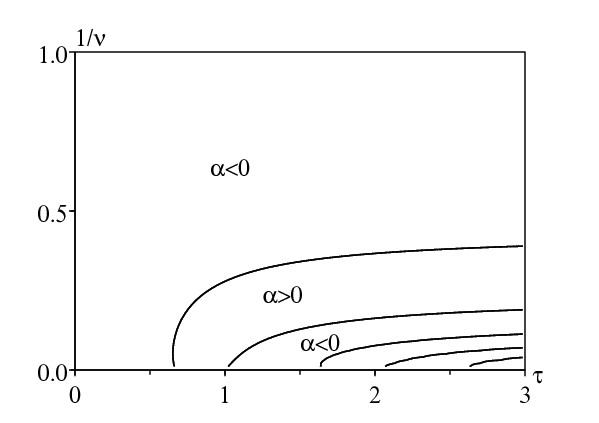
La figure 4 montre le signe de \(\alpha\) (plus précisément les lignes de niveau \(\alpha=0\)) dans le diagramme \((\tau,1/\nu)\). \(\alpha > 0\) est une condition necessaire pour la résonance. La ligne horizontale du haut \(\nu=1\) correspond au cas d'une période de latence distribuée exponentiellement et se trouve dans la partie du diagramme où \(\alpha < 0\), comme on s'y attend à la suite de la figure 2. La limite \(\sigma\to 0\) (ou \(1/\nu=\sigma^2/\tau^2\to 0\)) correspond à la période de latence fixée, donc la ligne horizontale du bas correspond à la figure 3 et présente plusieurs parties où \(\alpha > 0\). De cette manière, on voit comment la résonance disparaît lorsque la variance \(\sigma^2\) croît.
Évidemment la liste des modèles pourrait continuer jusqu'à la nausée :
De plus, comme le mentionne l'introduction, l'équation linéaire (1) se retrouve dans la plupart des problèmes de dynamique des populations (démographie, écologie, épidémiologie, théorie du chémostat, immunologie, etc). C'est l'approximation linéaire. Donc le même phénomène de résonance peut être étudié par exemple pour
La principale question qui demeure est de savoir si, pour certaines maladies particulières ou pour certaines applications dans d'autres domaines de la dynamique des populations, ce phénomène de résonance joue un rôle significatif. Comme on a vu, c'est une question difficile puisque pour des modèles très proches tels les modèles SEIR avec une période de latence exponentielle ou fixe, les conclusions sont différentes même si ces deux modèles pourraient convenir pour la même maladie. Les modèles avec \(\phi(x)\) à support compact sont cependant plus réalistes. Dans ce cas, l'équation d'Euler-Lotka a une infinité de racines complexes conjuguées. Donc il se peut que la résonance se produise pour certaines valeurs des paramètres.
La preuve suit celle pour le cas autonome. On part de (9). Puis on utilise la première équation de (2) et on intègre par parties: \begin{align*} \frac{\mathrm{d}V}{\mathrm{d}t} &= \int_0^\infty \Bigl [i(t,x)\, \frac{\partial v}{\partial t}+ \frac{\partial i}{\partial t}\, v(t,x)\Bigr ]\, \mathrm{d}x \\ &= \int_0^\infty \Bigl [i(t,x)\, \frac{\partial v}{\partial t}- \frac{\partial i}{\partial x}\, v(t,x) - \mu(t,x)\, i(t,x)\, v(t,x)\Bigr ]\, \mathrm{d}x\\ &= \int_0^\infty \Bigl [\frac{\partial v}{\partial t}+ \frac{\partial v}{\partial x} - \mu(t,x)\, v(t,x)\Bigr ] i(t,x)\, \mathrm{d}x +i(t,0)\, v(t,0)\, . \end{align*} En utilisant la seconde équation de (2) et (7), on obtient finalement \[\frac{\mathrm{d}V}{\mathrm{d}t} = \int_0^\infty \Bigl [\frac{\partial v}{\partial t}+ \frac{\partial v}{\partial x} - \mu(t,x)\, v(t,x)+v(t,0)\, \beta(t,x)\Bigr ] i(t,x)\, \mathrm{d}x = r \int_0^\infty \!\!\!v(t,x)\, i(t,x)\, \mathrm{d}x = r\, V(t)\, .\] Donc \(V(t)=V(0)\, e^{rt}\).
Remarque. Avec la définition (5) de \(u(t,x)\), \(i(t,x)=e^{rt}\, u(t,x)\) si \(i(0,x)=u(0,x)\). La croissance exponentielle de la valeur reproductive totale \(V(t)\) implique \[\int_0^\infty \!u(t,x)\, v(t,x)\, \mathrm{d}x = \int_0^\infty \!u(0,x)\, v(0,x)\, \mathrm{d}x, \quad \forall t > 0.\] La normalisation (8) prend la forme \[\int_0^\infty \!u(t,x)\, v(t,x)\, \mathrm{d}x =1,\] comme dans (Michel et coll., 2005).
Tout d'abord, noter avec (7) que la valeur reproductive est telle que \begin{equation} v(t,x)=\int_x^\infty \!\!\!v(t+y-x,0)\, e^{-r (y-x)}\times \frac{\ell(t-x,y)}{\ell(t-x,x)}\, \beta(t+y-x,y)\, \mathrm{d}y\, .\tag{26} \end{equation} On définit \begin{equation}\tag{27} c(t,x)=v(t+x,x)\, e^{-r(t+x)}\, . \end{equation} Alors (26) implique \begin{equation}\tag{28} c(t,x)=\int_0^\infty c(t+y,0)\, \frac{\ell(t,y)}{\ell(t,x)}\, \beta(t+y,y)\, \mathrm{d}y\, . \end{equation} Ediev (2007, équation (4)) a utilisé l'équation (28) comme point de départ pour essayer de généraliser le théorème de Fisher sur la croissance exponentielle de la valeur reproductive totale. Il a nommé \(c(t,x)\) le « potentiel démographique d'un personne d'âge x née à l'instant t ». En introduisant le « potentiel démographique total » au temps t \[C(t)=\int_0^\infty i(t,x)\, c(t-x,x)\, \mathrm{d}x\, ,\] Ediev (2007) put montrer d'abord que \(\mathrm{d}C/\mathrm{d}t=0\), c'est-à-dire que \(C(t)=C(0)\) est constant.
Fisher (1927) avait normalisé sa définition de la valeur reproductive de sorte que \(v(0)=1\) dans le cas où la fertilité et la mortalité ne dépendent pas du temps. (Ediev, 2007, équation (6)) choisit de généraliser la définition de la valeur reproductive avec \begin{equation}\tag{29} v^*(t,x)=\frac{c(t-x,x)}{c(t,0)}\, , \end{equation} où l'un utilise la notation avec une étoile \(v^*\) pour distinguer cette définition de la nôtre. Noter qu'en effet \(v^*(t,0)=1\) pour tout t.
La définition (29) pour la valeur reproductive dans le cas périodique n'a pas de « bonnes » propriétés. La raison en est que dans toute la théorie developpée jusqu'à présent, la valeur reproductive apparaît toujours comme une fonction propre (ou un vecteur propre dans le cadre discret) d'un certain opérateur linéaire. Voir par exemple (Grafen, 2006). Dans le cas autonome, la valeur reproductive n'est une fonction que de l'âge x (appelons-la \(v(x)\)). Donc ce n'est pas un problème de la normaliser de sorte que \(v(0)=1\). Mais avec des fertilités et des mortalités qui dépendent du temps (par exemple de manière périodique), la valeur reproductive est une fonction à la fois du temps t et de l'âge x. La liberté dans la normalisation de la fonction propre signifie que l'on n'a qu'un seul paramètre scalaire libre. Forcer \(v^*(t,0)=1\) pour tout t implique que la fonction \(v^*(t,x)\) ne peut être une fonction propre, sauf (vu (26)) si on a pour un certain r \begin{equation}\tag{30} 1=\int_0^\infty e^{-r y}\, \ell(t,y)\, \beta(t+y,y)\, \mathrm{d}y, \quad \forall t \end{equation} (Ediev, 2007, équation (7)). Mais (30) est presque sûrement faux, sauf si \(\ell(t,x)\) et \(\beta(t,x)\) ne dépendent pas du temps. Ediev (2007) dut supposer (30) pour montrer que la valeur reproductive totale, définie par \[\int_0^\infty i(t,x)\, v^*(t,x)\, \mathrm{d}x,\] grandit exponentiellement au taux r.
Si l'on veut vraiment définir la valeur reproductive à partir du potentiel démographique, on peut utiliser (27), c'est-à-dire \begin{equation}\tag{31} v(t,x)=c(t-x,x)\, e^{r t}\, . \end{equation} Ainsi, l'hypothèse improbable (30) n'est plus nécessaire pour démontrer la croissance exponentielle de la valeur reproductive totale. La définition (31) requiert bien sûr que r ait été prédéfini: cela peut être un problème si l'on considère comme dans (Ediev, 2007) des fertilités et des mortalités arbitraires et pas seulement périodiques. En utilisant (31) comme définition pour la valeur reproductive, on voit facilement que la constance de \(C(t)\) est équivalente à la croissance exponentielle de la valeur reproductive totale \(V(t)\) définie par (9) : \(V(t) = e^{rt} C(t)=e^{rt}\, C(0)=e^{rt}\, V(0)\).
Ce travail a reçu le soutien de la Fondation des sciences naturelles de l'Université du Xinjiang et du Programme de recherches avancées de coopérations franco-chinoises (PRA SI-05-01). Ce travail a été terminé alors que N. B. visitait le collège de mathématiques et sciences des systèmes de l'Université du Xinjiang à Urumqi, en Chine. On remercie M. Gyllenberg, R. M. Nisbet, R. Schoen et S. Tuljapurkar pour avoir envoyé des copies de leurs articles, et H. Caswell pour ses conseils.