Modélisation des épidémies conjuguées de tuberculose et de VIH dans un bidonville sud-africain

Résumé

On présente un modèle mathématique simple avec six compartiments pour l'interaction entre les épidémies de VIH et de tuberculose. Avec les données d'un bidonville près du Cap en Afrique du Sud, où la prévalence du VIH dépasse 20% et où le taux annuel de notification de la tuberculose est proche de 2000 pour 100000, on estime les paramètres du modèle. On étudie comment diverses mesures préventives pourraient changer le cours de ces épidémies. La promotion des préservatifs, une détection accrue de la tuberculose et la prophylaxie contre la tuberculose ont clairement un effet positif. L'impact des antirétroviraux sur l'incidence du VIH n'est pas évident et dépend de leur capacité à réduire la transmission sexuelle. Ces antirétroviraux réduiraient grandement le taux de notification de la tuberculose.

1.   Introduction

    En Afrique du Sud, 5,5 millions de personnes vivent avec le VIH, soit 12% de la population totale (ONUSIDA, 2006, p. 455). Environ 270000 cas de tuberculose active sont notifiés chaque année (OMS, 2007, p. 137). Environ 60% des adultes avec une tuberculose active sont porteurs du VIH; en effet, la coinfection avec le VIH et Mycobacterium tuberculosis (abrégé en M. tuberculosis) augmente considérablement la probabilité de progresser d'une tuberculose latente à une tuberculose active.

    (Lawn et coll., 2006a ; Wood et coll., 2007) ont étudié en détail ces épidémies dans un bidonville près de la ville du Cap. Le tableau 1 montre les estimations du taux de notification de la tuberculose, calculé à partir du nombre annuel de notifications et de deux recensements de la population conduits en 1996 et 2004, en supposant une évolution linéaire de la population entre ces deux années. Le tableau montre aussi la prévalence du VIH, estimée avec les données d'une clinique prénatale.

    En 2005, il y a eu 259 cas de tuberculose active notifiés parmi les adultes (d'âge ≥15 ans) (Wood et coll., 2007); 66% de ceux qui ont été testés pour le VIH étaient séropositifs. La population adulte était estimée à 10400 et la population totale à 13000. Donc le taux de notification de la tuberculose dans la population était de \(259/13\,000\simeq 1\,992\,\) pour 100000 habitants par an. De plus, dans un échantillon de la population constitué de 762 adultes, 12 personnes avaient une tuberculose active non diagnostiquée (3 séronégatifs et 9 séropositifs). Environ 23% (174/762) des personnes de l'échantillon étaient séropositives. Plus de 80% des cas de tuberculose à frottis positif ayant reçu un traitement furent guéris.

    Il y a eu dans la littérature médicale de nombreuses études focalisées sur des aspects particuliers des épidémies conjuguées de VIH et de tuberculose dans ce bidonville ou d'autres près de la ville du Cap (Badri et coll., 2002 ; Lawn et coll., 2005a, 2006a et 2006b ; Lawn et Wood, 2006a, 2006b et 2007 ; Wood et coll., 2007). On construit ici un modèle mathématique intégrant les données sur la tuberculose et le VIH pour mieux comprendre ces épidémies. On garde le modèle le plus simple qui soit cohérent avec les données disponibles; le modèle n'est pas structuré par âge. L'objectif principal est d'étudier l'impact de diverses mesures de prévention. Vus les niveaux extrêmement élevés de VIH et de tuberculose dans ce contexte, il est essentiel de savoir quelles mesures sont les plus efficaces. Un projet important pour contrôler le VIH et la tuberculose dans ce bidonville est en cours de préparation. Le modèle peut aider à planifier les interventions. En outre, le modèle et ses prédictions peuvent servir de cadre pour évaluer le succès ou l'échec des interventions.

    La section 2 passe en revue les modèles mathématiques combinant VIH et tuberculose. La section 3 introduit notre modèle, que l'on a essayé de garder le plus simple possible. La section 4 analyse quelques propriétés mathématiques de ce modèle. La section 5 passe en revue les valeurs des paramètres que l'on trouve dans la littérature médicale. La section 6 estime plusieurs paramètres en utilisant les données du bidonville sud-africain. La section 7 propose un diagramme de bifurcation qui montre qualitativement et quantitativement comment les états d'équilibre du modèle dépendent de certaines valeurs des paramètres. Cette approche est nécessaire car certains paramètres ne sont connus qu'approximativement. La section 8 étudie comment diverses interventions pourraient affecter les épidémies de VIH et de tuberculose. On étudie en particulier la dynamique transitoire puisque la convergence vers un état d'équilibre prend plusieurs décennies. La question principale est celle de l'impact des antirétroviraux sur le taux de notification de la tuberculose; la réponse n'est pas évidente. En effet, les personnes coinfectées sous antirétroviraux ont un risque réduit de 80% de développer une tuberculose active, mais leur espérance de vie est aussi plus longue. Comme leur risque de développer une tuberculose active est encore plusieurs fois supérieur à celui des personnes séronégatives, cela pourrait augmenter la transmission de la tuberculose. Nos résultats numériques suggèrent le contraire: les antirétroviraux pourraient diminuer considérablement le taux de notification de la tuberculose même si la prévalence du VIH s'en trouve augmentée. Cette conclusion doit être considérée avec précaution car il y a des incertitudes non seulement sur les valeurs des paramètres mais aussi sur la validité de la structure du modèle.

2.   Revue des modèles épidémiques avec VIH et tuberculose

    Le tableau 2 passe en revue les modèles épidémiques avec VIH et tuberculose. Les études sont essentiellement de deux types: soit des simulations informatiques du comportement transitoire de modèles réalistes mais complexes, soit des études mathématiques des états d'équilibre et de leur stabilité dans des modèles plus simples et moins réalistes. Ces modèles ont porté sur la situation en Afrique sub-saharienne, aux États-Unis, en Russie, en Inde ou dans les prisons brésiliennes. Certains modèles ont essayé de présenter une vue globale en considérant toutes les cinq régions de l'OMS. D'autres modèles ne portaient pas sur une région particulière. Les modèles combinent i classes pour le VIH et j classes pour la tuberculose. Ainsi on s'attend à ce que le modèle ait i×j compartiments. Certains modèles ont agrégé plusieurs compartiments tandis que d'autres ont ajouté plus de compartiments pour tenir compte d'interventions spécifiques. C'est pourquoi le tableau 2 indique le nombre de compartiments sous la forme i×j±k. Certains modèles prennent la forme d'un système d'équations différentielles. La plupart des autres utilisent des équations aux différences en temps discret. On mentionne enfin le travail en cours de Lungu (2007). Plusieurs autres modèles ont étudié de manière générique deux maladies infectant une même population; mais soit ils n'avaient pas de compartiment séparé pour les personnes coinfectées (Moghadas et Gumel, 2003), soit elles n'incluaient pas de période de latence (Blyuss et coll., 2005), qui est une caractéristique importante de la tuberculose.

    Tous ces modèles contiennent de nombreux paramètres inconnus mais reposent sur peu de données. Par exemple, il semblerait que (Currie et coll., 2003 ; Currie et coll., 2005 ; Hughes et coll., 2006 ; Raimundo et coll., 2003 ; West et Thompson, 1997) soient les seuls à ajuster leurs paramètres à la prévalence du VIH ou du SIDA et aux notifications de la tuberculose. Pour le bidonville sud-africain de notre étude, on a deux informations supplémentaires: le pourcentage de personnes séropositives parmi les cas de tuberculose notifiés et la prévalence de la tuberculose à une date. Ces deux contraintes supplémentaires devraient rendre nos estimations pour les paramètres plus robustes. De plus, le bidonville est certainement plus homogène que des pays entiers (les États-Unis dans (West et Thompson, 1997), le Kenya dans (Currie et coll., 2003 ; Currie et coll., 2005), le Zimbabwe dans (Hughes et coll., 2006)) et moins exceptionnel qu'une prison pour femmes (Raimundo et coll., 2003). Par ailleurs, on s'est concentré sur l'un des modèles les plus simples, avec un minimum de compartiments et de paramètres. Même ainsi, notre modèle contient 22 paramètres.

3.   Le modèle

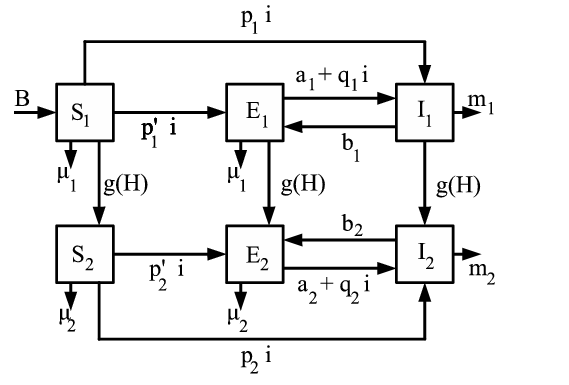
    Les compartiments de notre modèle combinent deux états pour le VIH (séronégatif et séropositif) avec trois états pour la tuberculose (sain, tuberculose latente et tuberculose active), comme dans (Moghadas et Gumel, 2002 ; Moghadas et Alexander, 2004 ; Singer et Kirschner, 2004). Le tableau 3 montre les six compartiments. L'indice 1 est pour les personnes séronégatives et l'indice 2 pour les personnes séropositives. Les personnes dans les compartiments \(\,E_1\), \(E_2\), \(I_1\) et \(I_2\,\) sont celles infectées par M. tuberculosis.

    Le tableau 4 montre les paramètres du modèle. Les paramètres physiologiques sont à peu près les mêmes à travers le monde ou au moins pour les personnes vivant en Afrique sub-saharienne: ce sont les mortalités \(\,\mu_1\) et \(\mu_2\), les paramètres pour la tuberculose \(p_1\), \(p_2\), \(q_1\), \(q_2\), \(a_1\), \(a_2\), \(m_1\) et \(m_2\). Au contraire, les paramètres « sociaux » dépendent de la région de l'étude, en particulier

• de la densité de population et des conditions de vie (taux de transmission \(k_1\) et \(k_2\)),
• de l'accès aux hôpitaux (taux de détection \(\gamma_1\) et \(\gamma_2\)),
• de la qualité du traitement (\(\varepsilon_1\) et \(\varepsilon_2\)),
• des habitudes sexuelles et des cofacteurs locaux pour la transmission du VIH tels que les autres maladies sexuellement transmissibles et la circoncision (\(d\)),
• de la vitesse à laquelle les informations sur le VIH diffusent (\(\lambda\))
• de l'historique de l'épidémie (\(t_0\)).

    Les équations de notre modèle sont \begin{align} \frac{dS_1}{dt} &= B - S_1\, (k_1\, I_1+k_2\, I_2)/P-\mu_1\, S_1 - f(H) \, H\, S_1\, ,\tag{1}\\ \frac{dE_1}{dt} &= (p'_1\, S_1-q_1\, E_1) (k_1\, I_1+k_2\, I_2)/P - (a_1+\mu_1)\, E_1 +b_1\, I_1 - f(H)\, H\, E_1\, ,\tag{2}\\ \frac{dI_1}{dt} &= (p_1\, S_1+q_1\, E_1) (k_1\, I_1+k_2\, I_2)/P - (b_1+m_1)\, I_1 + a_1\, E_1 - f(H)\, H\, I_1\, ,\tag{3} \end{align} pour les personnes séronégatives et \begin{align} \frac{dS_2}{dt} &= - S_2\, (k_1\, I_1+k_2\, I_2)/P -\mu_2\, S_2 + f(H)\, H\, S_1\, ,\tag{4}\\ \frac{dE_2}{dt} &= (p'_2\, S_2 - q_2\, E_2) (k_1\, I_1+k_2\, I_2)/P - (a_2+\mu_2)\, E_2 +b_2\, I_2 + f(H)\, H\, E_1\, ,\tag{5}\\ \frac{dI_2}{dt} &= (p_2\, S_2+q_2\, E_2) (k_1\, I_1+k_2\, I_2)/P - (b_2+m_2) I_2 + a_2\, E_2 + f(H)\, H\, I_1 \, ,\tag{6} \end{align} pour les personnes séropositives. La figure 1 montre les flux entre les différents compartiments.

    Le tableau 5 montre la correspondance que l'on utilise entre le vocabulaire médical et notre modèle. Le taux de notification de la tuberculose est le taux auquel les personnes dans les compartiments de tuberculose active sont détectées. Seule une fraction \(\,\varepsilon_1\) ou \(\varepsilon_2\,\) de celles-ci retournent réellement dans les compartiments de tuberculose latente. L'incidence de la tuberculose est le taux auquel les personnes entrent dans les compartiments de tuberculose active divisé par la population totale, donné d'habitude « pour 100000 personnes et par an ». Le taux d'infection par M. tuberculosis, qui est l'analogue en temps continu du risque annuel d'infection, est le taux auquel les personnes dans les compartiments sans tuberculose entrent dans les compartiments de tuberculose latente ou active. La prévalence de M. tuberculosis  est la proportion de la population totale dans les compartiments avec une tuberculose latente ou active. La prévalence de la tuberculose est la proportion de la population totale dans les compartiments avec une tuberculose active. Ceci inclut les tuberculoses actives, qu'elles n'aient pas été diagnostiquées ou qu'elles aient été détectées mais traitées sans succès.

    On utilise l'expression « quotient de Styblo » pour le quotient entre l'incidence de la tuberculose et le taux d'infection par M. tuberculosis, multiplié par 1000. Dans la littérature médicale, ce quotient est en général restreint aux notifications de la tuberculose à frottis positif (environ la moitié de toutes les notifications), avec une valeur supposée constante et égale à 50 pour les populations séronégatives. Autrement dit, un taux d'infection de 1% par an correspond à un taux d'incidence de 50 cas de tuberculose à frottis positif pour 100000 par an, soit environ 100 cas de tuberculose à frottis positif ou négatif pour 100000 par an. Cette hypothèse est appelée la « règle de Styblo » (Borgdorff, 2002). Cependant, comme on le verra dans le tableau 7, le quotient de Styblo ne peut plus être supposé le même dans les régions avec une prévalence élevée du VIH. Cette remarque met en doute la méthode utilisée par (Schulzer et coll., 1992).

    La réactivation endogène est la contribution à l'incidence de la tuberculose qui vient des compartiments de tuberculose latente avec les taux constants \(a_1\) ou \(a_2\). La réinfection exogène est la contribution qui vient des compartiments de tuberculose latente avec un taux qui dépend des nombres de cas de tuberculose active. La tuberculose primaire est la contribution venant directement des compartiments sans tuberculose.

    Notons un certain nombre de points importants:

• On suppose qu'une personne séropositive est introduite initialement dans une population stationnaire sans VIH où la tuberculose est endémique. On a choisi de mettre cette première personne avec le VIH dans le compartiment \(\,S_2\). Les formules pour \(\,S_1\), \(E_1\) et \(I_1\) à l'équilibre endémique pour la tuberculose se trouvent dans la section 4.1.
• L'âge et le sexe ne sont pas pris en compte. En particulier, le modèle ne peut distinguer les différentes routes de transmission du VIH, telles que la transmission sexuelle et la transmission de la mère à l'enfant. On ne distingue pas les tuberculoses pulmonaires et extra-pulmonaires, à frottis positif (infectieuse) et à frottis négatif (non-infectieuse) de manière à reduire au minimum le nombre de compartiments.
• La tuberculose résistante est encore assez limitée dans le bidonville sud-africain de notre étude. L'efficicacité du BCG n'est pas claire. Nous n'avons pas inclus ces aspects dans notre modèle.
• Dans l'équation (1), les naissances sont supposées constantes indépendamment du nombre de personnes qui meurent du SIDA ou de la tuberculose. Ainsi, notre modèle considère l'évolution de cohortes de tailles fixées à la naissance. Ce n'est pas trop déraisonnable si l'on n'utilise que des données
  • sur la prévalence du VIH, c'est-à-dire le pourcentage de la population vivant avec le VIH (et non le nombre total de personnes infectées),
  • sur le taux de notification de la tuberculose pour 100000 personnes et par an (et non le nombre total de cas notifiés par an).
  Si l'on supposait que les décès étaient remplacés par de nouveaux immigrants, il faudrait spécifier leur statut vis-à-vis de la tuberculose et du VIH. Il est difficile d'avoir des informations à ce sujet. Si par contre on supposait que les naissances étaient proportionnelles à la population, alors on ne pourrait plus étudier les équilibres. La démographie du bidonville est en réalité assez complexe. La population a grandi considérablement au cours de la dernière décennie. La pyramide des âges a un biais avec plus de jeunes adultes et peu d'enfants et de personnes âgées. Il y a aussi des entrées et des sorties dans la population.
• Dans les équations (1) et (4), on a choisi la « forme standard » pour l'infection et la réinfection par la tuberculose (Feng et coll., 2000 ; Sharomi et coll., 2008 ; Singer et Kirschner, 2004). On n'a pas choisi la « loi d'action de masse » utilisée par exemple dans (Gomes et coll., 2004 ; Moghadas et Gumel, 2002 ; Moghadas et Alexander, 2004). Avec des naissances constantes, la population totale décroît à mesure que l'épidémie de VIH de développe. Si l'on utilisait la « loi d'action de masse » pour la transmission de la tuberculose, le taux de transmission baisserait et cela ralentirait artificiellement l'épidémie de tuberculose.
• Dans les équations (1)-(3), on a aussi choisi la « forme standard » pour la transmission du VIH comme par exemple dans (Sharomi et coll., 2008). C'est la forme la plus utilisée pour les maladies sexuellement transmissibles. Comme dans (Williams et coll., 2006) mais contrairement à (Sharomi et coll., 2008), on suppose que le taux de transmission est une fonction exponentiellement décroissante de la prévalence du VIH. Cela inclut les changements comportementaux à mesure que les connaissances sur le VIH se répandent dans la population. (Williams et coll., 2006, supplément) a montré que cette fonction spéciale donne un bon ajustement aux données d'infection par le VIH dans une autre enquête en Afrique du Sud. Il est essentiel de garder la prévalence du VIH à des niveaux réalistes dans un modèle sans hétérogénéité dans les comportements sexuels.
• Tous les autres termes sont linéaires. En réalité, le taux de progression vers la tuberculose active est fonction du temps écoulé depuis l'infection: le taux est élevé pendant les deux premières années et faible pour le reste de la vie (Vynnycky et Fine, 1997). Bien sûr, il est possible de mettre cela en équations (Feng et coll., 2001). Mais pour garder le nombre de paramètres du modèle aussi petit que possible, on suppose qu'une certaine fraction des nouveaux infectés développe une tuberculose active immédiatement, tandis que le reste entre dans l'état latent avec une taux constant de progression vers la tuberculose active, comme dans (Gomes et coll., 2004 ; Moghadas et Gumel, 2002 ; Moghadas et Alexander, 2004 ; Porco et Blower, 1998 ; Singer et Kirschner, 2004). De même, on suppose qu'une certaine fraction des réinfections conduisent immédiatement à une tuberculose active comme dans (Feng et coll., 2000 ; Gomes et coll., 2004 ; Moghadas et Gumel, 2002 ; Moghadas et Alexander, 2004 ; Singer et Kirschner, 2004). Les autres réinfections sont « perdues » puisque les personnes sont déjà avec une tuberculose latente.
• Noter comment les équations modélisent les personnes dont le traitement est un échec. Ils sont comptés dans le taux de notification et induisent des taux de guérisons plus faibles parmi les cas de tuberculose active. Mais ils ne sont pas mis dans un compartiment séparé.

4.   Analyse mathématique

    L'état d'équilibre sans tuberculose et sans VIH est donné par \(S_1^0=B/\mu_1\) et \(E_1=I_1=S_2=E_2=I_2=0\).

4.1   Tuberculose seule

    Contexte. Le modèle avec la tuberculose mais sans VIH n'a que trois compartiments \(\,(S_1,E_1,I_1)\). Les équations sont (1)-(3) avec \(\,I_2=0\), \(H=0\) et \(P=S_1+E_1+I_1\) \begin{align} \frac{dS_1}{dt} &= B - k_1 S_1 I_1/P-\mu_1 S_1\, ,\tag{7}\\ \frac{dE_1}{dt} &= (p'_1\, S_1-q_1\, E_1)\, k_1 I_1/P - (a_1+\mu_1)\, E_1 +b_1 I_1 \, ,\tag{8}\\ \frac{dI_1}{dt} &= (p_1\, S_1+q_1\, E_1)\, k_1 I_1/P - (b_1+m_1)\, I_1 + a_1 E_1\, .\tag{9} \end{align} Ces équations sont, aux notations près, les mêmes que celles de (Singer et Kirschner, 2004, §3). (Feng et coll., 2000) étudie un modèle avec quatre compartiments (un compartiment de plus pour les personnes guéries) et avec réinfection mais sans progression primaire. Voir aussi la revue de (Castillo-Chavez et Song, 2004, §4.5). (Lipsitch et Murray, 2003) ont fait des remarques sur le modèle de (Feng et coll., 2000). (Singer et Kirschner, 2004) a essayé de montrer pour un modèle comprenant les trois routes conduisant à la tuberculose (progression primaire, réactivation et réinfection) qu'une bifurcation sous-critique se produit si le paramètre de réinfection est assez grand, comme (Feng et coll., 2000) l'a remarqué. Mais ce paramètre est trop grand pour être réaliste, comme (Lipsitch et Murray, 2003) l'a remarqué.

    À notre avis, il y a deux points faibles dans l'analyse de (Singer et Kirschner, 2004, §3). Le premier point est que, suivant l'idée de (Lipsitch et Murray, 2003), les paramètres réalistes doivent vérifier l'inégalité \(\,q_1\leq p_1\,\), puisque la tuberculose latente protège contre la progression rapide vers la tuberculose active en cas de réinfection (Vynnycky et Fine, 1997). Cette inégalité n'apparaît pas dans (Singer et Kirschner, 2004). Le second point faible est que le seuil donné par (Singer et Kirschner, 2004, équation (7)) est estimé en utilisant un échantillonage par hypercube latin des paramètres. Avec une telle méthode, la conclusion est probable mais non certaine, et peut dépendre du choix des paramètres. On va montrer ci-dessous que la bifurcation sous-critique se produit quand \(\,q_1\) est supérieur à un seuil \(q_1^*\), qui est toujours supérieur à \(p_1\). Ceci prouve que la bifurcation sous-critique ne se produit pas pour des valeurs réalistes des paramètres. Enfin, (Singer et Kirschner, 2004) n'a pas présenté les détails de l'analyse des états d'équilibre, ne présentant que les conclusions. Pour notre étude, on a besoin de la formule pour l'état d'équilibre endémique avec la tuberculeuse seule, car il sert de condition initiale pour le modèle complet avec la tuberculose et le VIH.

    On doit aussi mentionner ici les travaux (Moghadas et Gumel, 2002 ; Moghadas et Alexander, 2004) sur un modèle semblable à (7)-(9) mais avec une loi d'action de masse au lieu de la forme standard. Leur modèle suppose aussi implicitement que les personnes qui ont guéri de la tuberculose sont protégés pour le reste de leur vie (ils ne retournent pas dans l'état latent), une hypothèse quelque peu irréaliste. Formellement, cela correspond au cas \(\,b_1=0\,\) dans notre modèle. En dépit des remarques de (Lipsitch et Murray, 2003), (Moghadas et Alexander, 2004) prétend que la bifurcation sous-critique peut se produire pour des valeurs réalistes des paramètres. Noter cependant que les valeurs des paramètres utilisées dans (Moghadas et Alexander, 2004) pour \(\,k_1\), \(p_1\) et le produit \(k_1 q_1\) ne satisfont pas l'inégalité \(q_1\leq p_1\). Ces valeurs semblent donc irréalistes.

    Récemment, dans l'analyse d'un modèle avec VIH et tuberculose, (Sharomi et coll., 2008) ont étudié une extension du modèle à quatre compartiments pour la tuberculose avec réinfection introduit par (Feng et coll., 2000). Les auteurs ont étudié la bifurcation sous-critique qui se produit lorsque le quotient \(\,q_1/p_1\,\) est au-dessus d'un certain seuil. Mais ce seuil peut être supérieur à 1 (il est difficile de dire si tel est toujours le cas car les formules pour les modèles à quatre compartiments sont très compliquées). Et en effet, les auteurs ont choisi la quotient irréaliste \(\,q_1/p_1=\eta_r=3\) pour illustrer leurs résultats.

    Analyse. Linéarisons le système (7)-(9) près de l'état d'équilibre sans maladie. On obtient \[ \frac{dE_1}{dt} \simeq k_1 p'_1 I_1 - (a_1+\mu_1)\, E_1 +b_1 I_1\, ,\quad \frac{dI_1}{dt} \simeq k_1 p_1 I_1 - (b_1+m_1)\, I_1 + a_1 E_1 \, . \] Donc la reproductivité pour la tuberculose, telle que definie dans (Diekmann et Heesterbeek, 2000), est le rayon spectral de la matrice \[\left (\begin{array}{cc} 0 & \, k_1 p'_1\\ 0 & \, k_1 p_1\end{array}\right ) \left (\begin{array}{cc} a_1+\mu_1 & -b_1\\ -a_1 & b_1+m_1\end{array}\right )^{-1}\, ,\] qui se calcule facilement: \begin{equation}\tag{10} R_0^{\mathrm{TB}}= \frac{k_1 (a_1+p_1\, \mu_1)}{a_1 m_1+m_1 \mu_1+\mu_1 b_1} \, . \end{equation} Comme cette formule ne dépend pas du paramètre de réinfection, elle est identique à (Murphy et coll., 2003, équation (10)). C'est la même formule que celle dans (Feng et coll., 2000, §1) si \(\,b_1=0\) et \(p_1=0\). Une manière quelque peu plus intuitive d'obtenir (10) consiste à écrire que la reproductivité est l'espérance du nombre de cas secondaires produits par un cas infecté dans une population autrement sans maladie. Ce premier cas transmet M. tuberculosis à \(\,k_1\) personnes par unité de temps et reste infecté en moyenne \(1/(b_1+m_1)\,\) unités de temps. De plus, chaque personne nouvellement infectée sera immédiatement infectieuse avec une probabilité \(\,p_1\) et infectieuse seulement après réactivation avec une probabilité \((1-p_1)\, a_1/(a_1+\mu_1)\). Enfin, le premier cas peut redevenir infectieux après avoir guéri (éventuellement plusieurs fois), avec une probabilité qui est le produit de \(\,b_1/(b_1+\mu_1)\) et de \(a_1/(a_1+\mu_1)\). La formule suivante donne en effet le même résultat que (10) \begin{equation}\tag{11} R_0^{\mathrm{TB}}=\frac{k_1}{b_1+m_1} \Bigl [p_1+(1-p_1)\, \frac{a_1}{a_1+\mu_1}\Bigr ] \sum_{n=0}^\infty \Bigl (\frac{b_1}{b_1+m_1}\times \frac{a_1}{a_1+\mu_1}\Bigr )^n. \end{equation} Parce que la probabilité de développer une tuberculose active par réactivation \(\,a_1/(a_1+\mu_1)\) est petite, on obtient une bonne approximation pour la reproductivité en remplaçant la somme infinie dans (11) par son premier terme, qui est égal à 1.

    Cherchons un état d'équilibre endémique pour la tuberculose \[(S_1^*,E_1^*,I_1^*,0,0,0)\] dans le système (1)-(6) avec \(S_1^* > 0\), \(E_1^* > 0\) et \(I_1^* > 0\,\), c'est-à-dire un équilibre non trivial \((S_1^*,E_1^*,I_1^*)\,\) du système (7)-(9). Par commodité, on définit \begin{equation}\tag{12} P^*=S_1^*+E_1^*+I_1^*\, ,\quad s_1^*=S_1^*/P^*\, ,\quad e_1^*=E_1^*/P^*\, ,\quad i_1^*=I_1^*/P^*\, . \end{equation} Après des calculs laborieux, on peut montrer en partant de (7)-(9) que la fraction des cas de tuberculose active \(i_1^*\) doit être une racine positive de l'équation quadratique \begin{align} \bigl (i_1^*\bigr )^2 &+ \Bigl [\frac{a_1+b_1+(1-p_1)\, m_1+p_1 \mu_1}{q_1 k_1} + \frac{m_1}{k_1} - 1\Bigr ] i_1^* + \frac{a_1 m_1+m_1 \mu_1+\mu_1 b_1}{q_1 k_1^2}\, (1-R_0^{\mathrm{TB}})\,=\,0\, .\tag{13} \end{align} De plus, on a \begin{equation}\tag{14} e_1^*= i_1^*\, \frac{k_1-m_1-k_1 i_1^*}{\mu_1+k_1 i_1^*}\, ,\quad S_1^*=\frac{B}{k_1 i_1^*+\mu_1}\, , \end{equation} à partir desquels on peut calculer \begin{equation}\tag{15} s_1^*=1-e_1^*-i_1^*\, ,\quad P^*=S_1^*/s_1^*\, ,\quad E_1^*=e_1^* P^*\, ,\quad I_1^*=i_1^* P^*\, . \end{equation} Des équations quadratiques semblables à l'équation (13) se trouvent dans (Feng et coll., 2000, équation (A.1)) et (Moghadas et Gumel, 2002, équation (5.3)). On définit \begin{equation}\tag{16} k_1^*= \frac{a_1 m_1 + m_1 \mu_1+\mu_1 b_1}{a_1+p_1 \mu_1}\, . \end{equation} et \begin{equation}\tag{17} q_1^*=\frac{a_1+b_1+(1-p_1)\, m_1+p_1 \mu_1}{b_1+(1-p_1)\, m_1}\times \frac{a_1+p_1 \mu_1}{\mu_1}\, . \end{equation} Vu (10), on a \(R_0^{\mathrm{TB}}=k_1/k_1^*\). On a donc \(R_0^{\mathrm{TB}} < 1\) si \(k_1 < k_1^*\), et \(R_0^{\mathrm{TB}} > 1\) si \(k_1 > k_1^*\). Étudions les états d'équilibre de (7)-(9) dans l'espace des paramètres \((k_1,q_1)\). Dans l'appendice, on montre que:

• avec \(q_1 < q_1^*\,\), le système (7)-(9)
  • n'a pas d'état d'équilibre endémique lorsque \(\,0 < k_1 < k_1^*\),
  • a un équilibre endémique lorsque \(k_1 > k_1^*\).
  Il y a une bifurcation transcritique quand le paramètre \(\,k_1\) croît de 0 à \(+\infty\).
• avec \(q_1 > q_1^*\,\), il existe un autre seuil \(\widehat{k}_1(q_1) < k_1^*\), et
  • le système (7)-(9) n'a pas d'état d'équilibre endémique lorsque \(0 < k_1 < \widehat{k}_1(q_1)\),
  • le système a deux états d'équilibre endémiques lorsque \(\widehat{k}_1(q_1) < k_1 < k_1^*\),
  • le système a un seul état d'équilibre endémique lorsque \(k_1 > k_1^*\).
  Il y a une bifurcation sous-critique.

    Noter que la première fraction dans (17) est supérieure à 1 et que la seconde fraction est supérieure à \(p_1\). \(\,q_1^*\,\) est donc toujours supérieur à \(p_1\). Mais une valeur réaliste pour \(q_1\) est nécessairement inférieure à \(p_1\), comme on l'a déjà mentionné. Ceci montre que la zone des paramètres avec une bifurcation sous-critique est une curiosité mathématique qui ne se produit pas dans la pratique. Ceci confirme les remarques de (Lipsitch et Murray, 2003) et la conclusion suggérée par (Singer et Kirschner, 2004). Noter que la formule (17) pour \(\,q_1^*\) aurait pu être obtenue dans (Singer et Kirschner, 2004) si l'expression (16) pour \(k_1^*\) avait été insérée dans l'équation (7) de (Singer et Kirschner, 2004).

4.2   VIH seul

    Sans la tuberculose, le système (1)-(6) devient \begin{align} \frac{dS_1}{dt} = B -\mu_1\, S_1 - f(H) \, H\, S_1\,,\quad \frac{dS_2}{dt} = -\mu_2\, S_2 + f(H)\, H\, S_1\,\tag{18} \end{align} avec \(H=S_2/(S_1+S_2)\). (Hethcote et van den Driessche, 1991 ; Wang, 2006), entre autres, ont étudié des modèles épidémiques similaires avec un taux de contact qui dépend de manière non linéaire du nombre de personnes infectées. (Williams et coll., 2006) a utilisé un modèle plus compliqué pour la transmission du VIH avec un taux de contact qui dépend de manière non linéaire de la prévalence. Tout d'abord, linéarisons la seconde équation dans (18) près de l'équilibre sans maladie \(S_1=S_1^0\) et \(S_2=0\), \[\frac{dS_2}{dt} \simeq -\mu_2\, S_2 + f(0)\, S_2\, .\] Ainsi, la reproductivité pour le VIH est donnée par \[R_0^{\mathrm{VIH}} = f(0)/\mu_2\, .\] On vérifie facilement en utilisant (18) que l'état d'équilibre endémique avec VIH mais sans tuberculose est donné par \[\widehat{S}_1=\frac{B\, (1-\widehat{H})}{\mu_1 (1-\widehat{H}) + \mu_2\, \widehat{H}}\, ,\quad \widehat{S}_2=\frac{B\, \widehat{H}}{\mu_1\, (1-\widehat{H}) + \mu_2\, \widehat{H}}\, .\] \(\widehat{H}=\widehat{S}_2/(\widehat{S}_1+\widehat{S}_2)\,\) est la prévalence du VIH à l'équilibre. C'est la solution de l'équation \begin{equation}\tag{19} (1-\widehat{H})\, f(\widehat{H})=\mu_2 ,\quad \widehat{H} \in ]0,1[. \end{equation} Le côté gauche de (19) est une fonction décroissante, qui prend la valeur \(f(0)=d\) si \(\widehat{H}=0\) et la valeur 0 si \(\widehat{H}=1\). Donc l'équation (19) n'a pas de solution dans \(\,]0,1[\) si \(R_0^{\mathrm{VIH}} < 1\) et exactement une solution dans \(]0,1[\) si \(R_0^{\mathrm{VIH}} > 1\).

4.3   VIH et tuberculose

    L'état d'équilibre endémique avec la tuberculose peut être envahi par le VIH. Linéarisons le système (4)-(6) près de cet équilibre et utilisons les notations de (12). On obtient \begin{align*} \frac{dS_2}{dt} &\simeq - k_1 S_2\, i_1^* -\mu_2\, S_2\, + f(0)\, s_1^*\, (S_2+E_2+I_2)\, ,\\ \frac{dE_2}{dt} &\simeq k_1\, (p'_2\, S_2 - q_2\, E_2)\, i_1^* - (a_2+\mu_2)\, E_2 +b_2\, I_2 + f(0)\, e_1^*\, (S_2+E_2+I_2)\, ,\\ \frac{dI_2}{dt} &\simeq k_1\, (p_2\, S_2+q_2\, E_2)\, i_1^* - (b_2+m_2)\, I_2 + a_2\, E_2 + f(0)\, i_1^*\, (S_2+E_2+I_2)\, . \end{align*} Donc la reproductivité \(r_0^{\mathrm{VIH}}\) pour le VIH introduit dans une population avec la tuberculose endémique est le rayon spectral de la matrice \begin{equation}\tag{20} f(0) \left (\begin{array}{ccc} s_1^* & s_1^* & s_1^*\\ e_1^* & e_1^* & e_1^*\\ i_1^* & i_1^* & i_1^* \end{array}\right ) \left (\begin{array}{ccc} k_1 i_1^*+\mu_2 & 0 & 0\\ -k_1 p'_2\, i_1^* &\,k_1 q_2\, i_1^*+a_2+\mu_2 & -b_2\\ -k_1 p_2\, i_1^* & -k_1 q_2\, i_1^*-a_2 & \,b_2+m_2\end{array}\right )^{-1}\, . \end{equation} Cette matrice est de rang 1, donc son rayon spectral est égal à sa trace. Ainsi on obtient \[r_0^{\mathrm{VIH}}=f(0)\, (s_1^*\, \tau_{S_2}+e_1^*\, \tau_{E_2} + i_1^*\, \tau_{I_2})\, .\] \(\tau_{S_2}\), \(\tau_{E_2}\) et \(\tau_{I_2}\,\) sont des expressions complexes avec une interpretation simple. Par exemple, \(\,\tau_{S_2}\) est l'espérance de vie d'une personne à partir du moment où elle entre dans le compartiment \(S_2\,\) (dans le modèle linéarisé). En particulier, \(\,\tau_{S_2}\), \(\tau_{E_2}\) et \(\tau_{I_2}\) sont tous strictement inférieur à \(1/\mu_2\) si \(m_2 > \mu_2\,\) (comme il se doit). On a donc \[r_0^{\mathrm{VIH}} < R_0^{\mathrm{VIH}} .\] Sans surprise, l'espérance du nombre de cas secondaires produits par une personne séropositive « moyenne » dans une population avec la tuberculose endémique est inférieure à celle dans une population sans tuberculose, puisque la tuberculose active raccourcit la vie d'une telle personne.

    De même, l'équilibre endémique avec le VIH peut être envahi par la tuberculose. Linéarisons les équations (2)-(3)-(5)-(6) près de \((\widehat{S}_1,0,0,\widehat{S}_2,0,0)\). On définit \[\widehat{P}=\widehat{S}_1+\widehat{S}_2\, ,\quad \widehat{s}_1=\widehat{S}_1/\widehat{P}=1-\widehat{H}\, ,\quad \widehat{s}_2=\widehat{S}_2/\widehat{P}=\widehat{H}\, .\] On obtient \begin{align*} \frac{dE_1}{dt} &\simeq p'_1 \widehat{s_1} (k_1 I_1+k_2\, I_2) - (a_1+\mu_1)\, E_1 +b_1\, I_1 - f(\widehat{H})\, \widehat{H}\, E_1\, ,\\ \frac{dI_1}{dt} &\simeq p_1 \widehat{s_1} (k_1 I_1+k_2\, I_2) - (b_1+m_1)\, I_1 + a_1\, E_1 - f(\widehat{H})\, \widehat{H}\, I_1\, ,\\ \frac{dE_2}{dt} &\simeq p'_2 \widehat{s_2}\, (k_1 I_1+k_2\, I_2) - (a_2+\mu_2)\, E_2 +b_2\, I_2 + f(\widehat{H})\, \widehat{H}\, E_1\, ,\\ \frac{dI_2}{dt} &\simeq p_2 \widehat{s_2}\, (k_1 I_1+k_2\, I_2) - (b_2+m_2) I_2 + a_2\, E_2 + f(\widehat{H})\, \widehat{H}\, I_1 \, . \end{align*} Donc la reproductivité \(r_0^{\mathrm{TB}}\) pour la tuberculose introduite dans une population avec le VIH qui est endémique est le rayon spectral de la matrice \(M\, N^{-1}\), avec \begin{equation}\tag{21} M= \left (\begin{array}{cccc} 0 & \,p'_1 k_1 \widehat{s_1} &\,0 &\,p'_1 k_2\, \widehat{s_1}\\ 0 & \,p_1 k_1 \widehat{s_1} &\,0 &\,p_1 k_2\, \widehat{s_1}\\ 0 & \,p'_2\, k_1 \widehat{s_2} &\,0 &\,p'_2 k_2\, \widehat{s_2}\\ 0 & \,p_2\, k_1 \widehat{s_2} &\,0 &\,p_2\, k_2\, \widehat{s_2} \end{array}\right ) \end{equation} et \[N= \left (\begin{array}{cccc} a_1+\mu_1+f(\widehat{H})\, \widehat{H} & -b_1 & 0 & 0\\ -a_1 &\,b_1+m_1+f(\widehat{H})\, \widehat{H} & 0 & 0\\ -f(\widehat{H})\, \widehat{H} & 0 &\,a_2+\mu_2 & -b_2\\ 0 & - f(\widehat{H})\, \widehat{H} & -a_2 &\,b_2+m_2 \end{array}\right )\, .\] Il semblerait que \(r_0^{\mathrm{TB}}\) puisse être supérieur ou inférieur à \(R_0^{\mathrm{TB}}\) selon les valeurs numériques des paramètres.

    Supposons de manière réaliste que \(q_1\leq p_1\), de sorte qu'il n'y a pas de bifurcation sous-critique pour le modèle avec tuberculose mais sans VIH. Cette analyse de stabilité linéaire suggère la conjecture suivante:

• l'état d'équilibre sans aucune maladie est un attracteur global du système (1)-(6) si \(\,R_0^{\mathrm{VIH}} < 1\) et \(R_0^{\mathrm{TB}} < 1\),
• l'état d'équilibre avec le VIH endémique est un attracteur global si \(\,R_0^{\mathrm{VIH}} > 1\) et \(r_0^{\mathrm{TB}} < 1\),
• l'état d'équilibre avec la tuberculose endémique est un attracteur global si \(\,R_0^{\mathrm{TB}} > 1\) et \(r_0^{\mathrm{VIH}} < 1\),
• dans les autres cas, il y a un état d'équilibre endémique avec à la fois le VIH et la tuberculose, qui doit être calculé numériquement, et qui est un attracteur global.

• \(R_0^{\mathrm{VIH}} > 1\), \(r_0^{\mathrm{TB}} > 1\), \(R_0^{\mathrm{TB}} > 1\) et \(r_0^{\mathrm{VIH}} > 1\). Les états d'équilibre avec le VIH seul et avec la tuberculose seule existent mais chaque état d'équilibre est un point selle.
• \(R_0^{\mathrm{VIH}} > 1\), \(r_0^{\mathrm{TB}} > 1\) et \(R_0^{\mathrm{TB}} < 1\). L'état d'équilibre avec le VIH seul existe mais c'est un point selle. Il n'y a pas d'état d'équilibre avec la tuberculose seule.

5.   Valeurs des paramètres selon la littérature médicale

5.1   Paramètres démographiques

    On a pris une mortalité naturelle \(\mu_1=\mbox{0,02}\,\) par an comme par exemple dans (Cohen et coll., 2006), ce qui correspond à une espérance de vie de 50 ans. C'est un peu pessimiste même dans une zone où les habitants vivent dans une très grande pauvreté comme le bidonville sud-africain de notre étude. La mortalité est 0,0064 par an dans (Heymann, 1993), 0,0081 par an dans (Guwatudde et coll., 2004) et 0,0167 par an dans (Raimundo et coll., 2002). Noter que les mortalités dans (Guwatudde et coll., 2004 ; Heymann, 1993) correspondent à des espérances de vie bien trop élevées.

    On a choisi les naissances B pour avoir une population totale dans l'équilibre sans maladie (\(S_1=B/\mu_1\)) de 10000, la taille approximative du bidonville (Lawn et coll., 2006a). Ainsi B=200 par an.

5.2   Paramètres du VIH pour les personnes non infectées par M. tuberculosis

    On a pris pour la mortalité des personnes séropositives \(\mu_2=\mbox{0,1}\,\) par an comme dans (Cohen et coll., 2006) pour avoir une survie moyenne de 10 ans. Cette mortalité était 0,13 par an dans (Heymann, 1993) et dans (Guwatudde et coll., 2004), d'après une étude en Ouganda (Nunn et coll., 1997). Schulzer et coll. (1992) ont supposé une durée fixe de survie de dix ans.

5.3   Paramètres de la tuberculose pour les personnes séronégatives

    Les paramètres de progression vers la tuberculose active, \(p_1\) et \(a_1\). On a déjà mentionné que le taux de progression vers la tuberculose active est une fonction décroissante du temps écoulé depuis l'infection. À partir de données des Pays-Bas pour la période 1951-1970, (Sutherland et coll., 1982) a estimé que les hommes ont 5% de risque annuel de développer une tuberculose primaire pendant les cinq années suivant l'infection et 0,025% de risque annuel de réactivation après cinq années. Pour les femmes, les chiffres étaient 6% et 0,002%. (Vynnycky et Fine, 1997) a fait une étude similaire avec des données de l'Angleterre et du Pays de Galles pour la période 1953-1988. Pour les individus âgés de plus de 20 ans, l'estimation pour le risque cumulé pendant les cinq premières années était de 14%, avec un risque d'environ 8% pendant la première année, 3% pendant la deuxième année, 1% pendant la troisième année. Le risque de réactivation par la suite était de 0,03% par an. Pour les individus de moins de 10 ans et ceux de 15 ans, le risque cumulé pour les cinq premières années était respectivement de 4% et de 9%, tandis que le risque de réactivation était proche de 0 et de 0,015% par an. Noter que le risque cumulé durant les cinq premières années dans (Sutherland et coll., 1982) est d'environ 25%, nettement plus que les 14% de (Vynnycky et Fine, 1997).

    Notre modèle n'inclut pas le temps écoulé depuis l'infection mais suppose qu'une certaine fraction des nouvelles infections développe la tuberculose immédiatement tandis que le reste entre dans une phase latente où le taux de progression vers la tuberculose active est constant. On suppose, comme dans les estimations plus récentes de (Vynnycky et Fine), que \(\,p_1=11\%\) (l'estimation pour le risque cumulé lors des deux premières années) et \(a_1=\mbox{0,03}\%\) par an.

    Vue la mortalité naturelle \(\mu_1\) choisie précédemment, ces valeurs de paramètres correspondent à une probabilité de progresser de la tuberculose latente à la tuberculose active \[a_1/(a_1+\mu_1)\simeq \mbox{1,5}\%,\] et à une probabilité totale de développer une tuberculose active après une infection par M. tuberculosis \[p_1+a_1/(a_1+\mu_1)\simeq \mbox{12,5}\%.\] Il n'est cependant pas certain que des estimations de paramètres pour la progression de la tuberculose chez des Britanniques soient applicables à des Africains qui vivent dans des conditions très différentes. On aurait besoin de plus de données sur ce sujet.

    En comparaison, le pourcentage de personnes séronégatives qui progressent rapidement vers une tuberculose active était

• 5% dans (Schulzer et coll., 1992) (la première année; pas de référence),
• 5% dans (West et Thompson, 1997) (après une courte période de latence d'environ un an; pas de référence),
• 5% dans (Guwatudde et coll., 2004) (progression immédiate; pas de référence),
• 5% par an dans (Raimundo et coll., 2002) (risque constant; pas de référence),
• 7% dans (Dowdy et coll., 2006) (progression immédiate; d'après (Veening, 1968)),
• 14% dans (Cohen et coll., 2006) (après une courte période de latence d'environ un an; d'après (Sutherland et coll., 1982) et d'autres références),
• 14% dans (Hughes et coll., 2006) (au cours des cinq premières années; d'après (Sutherland et coll., 1982 ; Vynnycky et Fine, 1997) et d'autres références).

• 0,01% par an dans (Cohen et coll., 2006) (d'après (Vynnycky et Fine, 1997) et d'autres références),
• 0,074% par an dans (Guwatudde et coll., 2004),
• 0,1% par an dans (Dowdy et coll., 2006)
• 0,1% par an dans (Hughes et coll., 2006) (après cinq années d'infection, d'après (Vynnycky et Fine, 1997)).

    Infection et réinfection: \(q_1/p_1\). (Sutherland et coll., 1982) estime qu'une infection latente avec M. tuberculosis  réduit le risque de maladie après réinfection de 63% pour les hommes séronégatifs et de 81% pour les femmes séronégatives. (Vynnycky et Fine, 1997) trouve une réduction du risque de 16% parmi les adolescents séronégatifs et de 41% parmi les adultes séronégatifs. Le modèle de (Cohen et coll., 2006) suppose une réduction de risque de 65% pour les personnes séronégatives, d'après (Sutherland et coll., 1982 ; Vynnycky et Fine, 1997). (Dowdy et coll., 2006) suppose une réduction de 72% pour les personnes séronégatives et pour les personnes séropositives depuis peu, d'après (Sutherland et coll., 1982). Ces deux études suivent les résultats de (Sutherland et coll., 1982) plutôt que ceux plus récents de (Vynnycky et Fine, 1997). On préfère ici utiliser une moyenne des valeurs de (Vynnycky et Fine, 1997). On suppose que \(q_1/p_1=\mbox{0,7}\,\). Ceci correspond à une réduction de 30% du risque pour les personnes séronégatives.

    La mortalité \(m_1\) et le taux de guérison naturelle \(\beta_1\). Les données sur la mortalité due à la tuberculose sans traitement remontent à l'époque où il n'y avait pas de traitement efficace, au début du XXe siècle. La probabilité de mourir [\(m_1/(m_1+\beta_1)\)] était alors d'environ 50%. C'est l'estimation mentionnée dans (Murray et coll., 1990). (Corbett et coll., 2003b, tableau 1) estime que la maladie pour les personnes séronégatives non traitées pour la tuberculose [\(1/(m_1+\beta_1)\)] dure approximativement 2 ans. Ces deux estimations pour \(\,1/(m_1+\beta_1)\) et \(m_1/(m_1+\beta_1)\) donnent \(m_1=\mbox{0,25}\) par an et \(\beta_1=\mbox{0,25}\,\) par an. Ce sont les valeurs que l'on prend pour notre modèle. Un autre modèle a supposé 35% de mortalité après un an (Heymann, 1993, p. 407). Parmi les modèles qui ont pris des mortalités différentes pour les cas de tuberculose non traitée qui sont infectieux ou non infectieux, les mortalités étaient 0,3 et 0,2 par an respectivement (Cohen et coll., 2006), ou 35% et 10% après un an (Dowdy et coll., 2006). (Cohen et coll., 2006) a supposé que le taux auquel les cas séronégatifs de tuberculose non traitée retournent au stade latent [\(\beta_1\)] était 0,2 par an. Toutes ces valeurs ne sont pas trop éloignées de celles que l'on a choisies.

5.4   Paramètres impliquant à la fois le VIH et la tuberculose

    Le quotient d'infectiosité \(k_2/k_1\). Les cas de tuberculose qui sont séropositifs sont en moyenne moins infectieux que ceux qui sont séronégatifs, car la tuberculose extrapulmonaire se produit plus souvent chez les personnes séropositives. Les modèles ont souvent séparé les compartiments pour les cas de tuberculose active en deux (qu'ils soient séronégatifs ou séropositifs), avec un sous-compartiment pour la tuberculose infectieuse et un sous-compartment pour la tuberculose non infectieuse. Les pourcentages des cas de tuberculose séronégatifs et séropositifs qui sont infectieux étaient de 50% et 40% dans (Schulzer et coll., 1992), 57% et 50% dans (Guwatudde et coll., 2004), 45% et 30% dans (Cohen et coll., 2006). Dans notre modèle, on ne distingue pas les cas de tuberculose infectieuse de ceux qui ne le sont pas. On utilise une infectiosité moyenne \(\,k_1\) pour tous les cas de tuberculose séronégatifs et une infectiosité moyenne \(k_2\,\) pour tous les cas de tuberculose séropositifs. Vue la structure de notre modèle, la différence d'infectiosité peut être prise en compte en choisissant une valeur appropriée pour le quotient \(k_2/k_1\). Avec les valeurs numériques de (Cohen et coll., 2006), on suppose que \(k_2/k_1=30/45=2/3\).

    Le taux de progression \(a_2\) vers la tuberculose active pour les personnes séropositives.   Comme pour les personnes séronégatives, le taux de progression vers la tuberculose active dépend du temps écoulé depuis l'infection mais aussi du stade d'infection par le VIH. Cependant, notre modèle ne distingue pas les stades d'infection par le VIH. On se contentera donc d'estimations qui sont des moyennes sur tous les stades. Pour des utilisateurs de drogue séropositifs aux États-Unis, (Selwyn et coll., 1989 et 1992) a trouvé un taux de progression moyen entre 0,079 et 0,097 par an. Dans la ville du Cap, (Badri et coll., 2002) a trouvé une incidence moyenne de la tuberculose (comprenant à la fois la réactivation, la progression rapide et la réinfection) de 0,097 par an. Mais l'incidence de la tuberculose atteignait 0,24 par an parmi les personnes séropositives dans les stades 3 et 4 selon l'OMS (Badri et coll., 2002). À la suite de (Selwyn et coll., 1989 et 1992), on suppose que le taux de réactivation de notre modèle est \(\,a_2=\mbox{0,08}\,\) par an, ce qui semble aussi compatible avec les données de (Badri et coll., 2002). (Heymann, 1993) a aussi utilisé l'estimation de (Selwyn et coll., 1989 et 1992) dans son modèle. D'autres études ont utilisé 0,0074 par an (Guwatudde et coll., 2004) (en supposant une multiplication par dix par rapport aux personnes séronégatives), 0,05 par an (Raimundo et coll., 2002) ou 0,17 par an (Cohen et coll., 2006) (sans référence). (Schulzer et coll., 1992) a utilisé un modèle plus compliqué qui distingue si l'infection par M. tuberculosis s'est produite avant ou après l'infection par le VIH. Noter à nouveau le désaccord entre les valeurs des paramètres.

    Infection et réinfection: \(q_2/p_2\). Il y a peu de données sur la réinfection pour les personnes séropositives. Dans l'épidémie de tuberculose étudiée dans (Di Perri et coll., 1989), aucun des quatre individus qui avaient déjà un test tuberculinique positif n'a développé la tuberculose. (Cohen et coll., 2006, supplément, tableau 2) suppose une réduction du risque de 25% pour les personnes séropositives (sans référence). (Dowdy et coll., 2006) suppose une réduction de 25% pour les personnes avec le SIDA (d'après (Currie et coll., 2003)). On suppose ici comme dans (Cohen et coll., 2006) que \(\,q_2/p_2=\mbox{0,75}\). Mais plus de données seraient nécessaires pour confirmation. Rappelons qu'on a supposé que \(q_1/p_1=\mbox{0,7}\) pour les personnes séronégatives.

    La mortalité \(m_2\) et le taux de guérison naturelle \(\beta_2\). La mortalité pour les cas de tuberculose séropositifs [\(m_2\)] était 0,325 par an dans (Guwatudde et coll., 2004) (d'après Elliott et coll., 1995) et 1,0 par an dans (Cohen et coll., 2006) (d'après (Nunn et coll., 1997)) à la fois pour la tuberculose infectieuse et la tuberculose non infectieuse. Le taux auquel les cas de tuberculose non traités et séropositifs retournent au stade latent [\(\beta_2\)] était 0,1 par an dans (Cohen et coll., 2006). Pour notre modèle, on utilise encore les données de (Corbett et coll., 2003b, tableau 1): la durée moyenne de la maladie pour les cas séropositifs de tuberculose non traitée [\(1/(m_2+\beta_2)\)] est 0,5 an. Dans la même référence, la probabilité de mourir [\(m_2/(m_2+\beta_2)\)] est 81% pour la tuberculose infectieuse (35% de tous les cas) et 76% pour la tuberculose non infectieuse (65% de tous les cas): on utilise la moyenne pondérée, qui est proche de 80%. Ces deux estimations pour \(\,1/(m_2+\beta_2)\) et \(m_2/(m_2+\beta_2)\) donnent \(m_2=\mbox{1,6}\) par an et \(\beta_2=\mbox{0,4}\) par an.

6.   Estimation des autres paramètres à partir des données sud-africaines

    Proportions de succès des traitements, \(\,\varepsilon_1\) et \(\varepsilon_2\). La proportion de succès des traitements est d'environ 80% (Wood et coll., 2007). On prend cette valeur pour \(\,\varepsilon_1\) et \(\varepsilon_2\).

    Les taux de détection \(\gamma_1\) et \(\gamma_2\). (Wood et coll., 2007) indique que 259 cas de tuberculose ont été notifiés parmi les adultes (âge ≥15) en 2005; 66% de ceux qui ont été testés pour le VIH étaient séropositifs. La population adulte était cette année-là d'environ 10400. De plus, dans un échantillon de la population de 762 adultes, 12 avaient une tuberculose non diagnostiquée (3 séronégatifs et 9 séropositifs). On s'attend donc à ce que les relations suivantes soient vraies: \begin{align} &\gamma_1\, I_1^{\mathrm{adulte}} \simeq 34\% \times 259,\quad I_1^{\mathrm{adulte}}\simeq 10\,400\times 3/762\, ,\tag{22}\\ &\gamma_2\, I_2^{\mathrm{adulte}}\simeq 66\% \times 259\, ,\quad I_2^{\mathrm{adulte}}\simeq 10\,400 \times 9/762\, .\tag{23} \end{align} Ceci donne les estimations \(\gamma_1\simeq \mbox{2,2}\) par an et \(\gamma_2\simeq \mbox{1,4}\,\) par an. Mais noter que puisque les quotients 3/762 et 9/762 sont petits, l'incertitude est grande: les intervalles de confiance binômiaux à 95% pour les quotients 3/762 et 9/762 sont respectivement [0,08% 1,15%] et [0,54% 2,23%]. Avec (22)-(23), l'intervalle de confiance pour \(\,\gamma_1\) est [0,74 10,6] par an, et celui pour \(\gamma_2\,\) est [0,74 3,0] par an. (Corbett et coll., 2004) suggère \(\,\gamma_2 > \gamma_1\). Pour notre modèle, on a choisi

• la borne inférieure de l'intervalle de confiance pour \(\gamma_1\), \(\gamma_1=\mbox{0,74}\) par an,
• la borne supérieure de l'intervalle de confiance pour \(\gamma_2\), \(\gamma_2=\mbox{3,0}\) par an.

    Avec ces choix, on obtient \(b_1=\beta_1+\gamma_1 \varepsilon_1\simeq \mbox{0,84}\) par an et \(b_2=\beta_2+\gamma_2 \varepsilon_2\simeq \mbox{2,8}\,\) par an. En comparaison, les valeurs de \(\,b_1\) et \(b_2\,\) pour tout l'Ouganda dans (Guwatudde et coll., 2004) étaient toutes les deux 0,3 par an. Mais la détection des cas n'est probablement pas aussi bonne que dans le bidonville sud-africain de notre étude.

    On remarque aussi que les probabilités pour que la tuberculose soit détectée sont \[\frac{\gamma_1}{m_1+\beta_1+\gamma_1}\simeq 60\% ,\quad \frac{\gamma_2}{m_2+\beta_2+\gamma_2}\simeq 60\%\, .\] Quoique la mortalité \(m_2\) soit élevée, la probabilité de détection des cas de tuberculose séropositifs est le même que celui des personnes séronégatives à cause de la valeur élevée de \(\gamma_2\,\) utilisée ici. Rappelons que l'objectif fixé par l'OMS pour la probabilité de détection est 70%. La durée moyenne de la maladie est \[\frac{1}{b_1+m_1}\simeq \mbox{0,92}\, ,\quad \frac{1}{b_2+m_2}\simeq \mbox{0,23}\, \] années. En comparaison, (Corbett et coll., 2004) a estimé la durée de la maladie (avec frottis positif) avant le diagnostic pour des personnes qui travaillent dans des mines sud-africaines : 1,15 an pour les personnes séronégatives, 0,17 an pour les personnes séropositives.

    Le taux de transmission de M. tuberculosis \(k_1\). Le taux moyen de notification de la tuberculose dans la décennie avant 1995 en Afrique du Sud, c'est-à-dire avant la montée de la prévalence du VIH, était d'environ 200 pour 100000 et par an ; voir (Williams et Maher, 2007) et (OMS, 2007, p. 184). C'est aussi une estimation raisonnable pour le bidonville de notre étude, vues les données du tableau 1. Dans notre modèle, le taux de notification de la tuberculose quand il n'y a pas de VIH est \(\gamma_1\, i_1^*\). Avec l'équation (13) pour \(\,i_1^*\,\), on peut estimer le seul paramètre inconnu qui reste: \(k_1\). On obtient \(\,k_1=\mbox{11,4}\,\) par an, ce qui correspond à un taux de notification de 203 pour 100000 et par an. D'après (Murray et coll., 1990), chaque personne séronégative avec une tuberculose non diagnostiquée à frottis positif infecte entre 10 et 14 personnes par an. Si les cas à frottis positif représentent la moitié de tous les cas, un cas de tuberculose séronégatif provoque en moyenne 5 à 7 infections par an. Cette plage de valeurs est compatible avec notre estimation \(k_1=\mbox{11,4}\,\) par an pour le taux maximum d'infection dans une population complètement saine. Si par exemple x=60% de la population est déjà infectée par M. tuberculosis, alors un cas de tuberculose active infecte environ \(\,x\, k_1\) personnes saines par an.

    Les paramètres \(d\), \(\lambda\) et \(t_0\,\) pour le VIH. Faisons la somme des trois équations (1)-(3) pour les personnes séronégatives et des trois équations (4)-(6) pour les personnes séropositives. On définit \(\,X_1=S_1+E_1+I_1\) et \(X_2=S_2+E_2+I_2\). \(\,H=X_2/(X_1+X_2)\,\) est la prévalence du VIH. On obtient le système \begin{align} \frac{dX_1}{dt}&=B - \mu_1\, X_1 - f(H)\, H\, X_1 +(\mu_1-m_1)\, I_1\,,\tag{24}\\ \frac{dX_2}{dt}&=-\mu_2\, X_2+f(H)\, H\, X_1 + (\mu_2-m_2)\, I_2\,.\tag{25} \end{align} Pour obtenir une première estimation de d, λ et \(t_0\,\), on néglige les termes contenant \(I_1\) et \(I_2\,\), car les cas de tuberculose active ne forment qu'une petite proportion de la population. Le système résultant ne fait intervenir que \(X_1\) et \(X_2\), il est formellement identique au système (18) pour le VIH sans la tuberculose. Prenons \(X_1(t_0)=B/\mu_1\) et \(X_2(t_0)=1\). On obtient un bon ajustement à la prévalence du VIH donnée dans le tableau 1 avec \(\,d=\mbox{0,7}\)/an, \(\lambda=\mbox{5,9}\) et \(\,t_0=1984\,\) pour le début de l'épidémie de VIH. Trois paramètres sont nécessaires et souvent suffisants pour ajuster un ensemble quelconque de nombres croissants qui suivent à peu près une courbe logistique, comme c'est le cas ici. Rappelons que d, λ et \(t_0\) ne peuvent pas provenir d'études concernant d'autres localités ou régions.

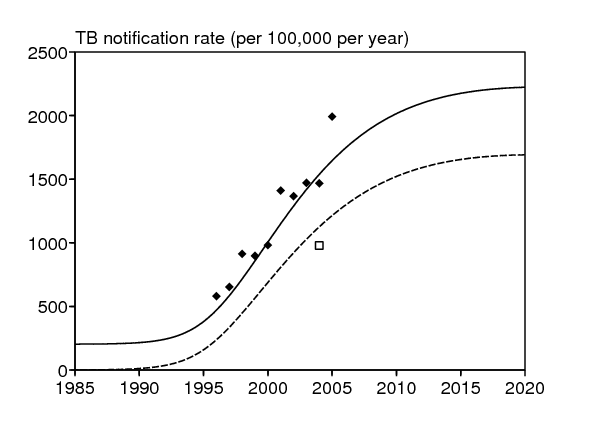
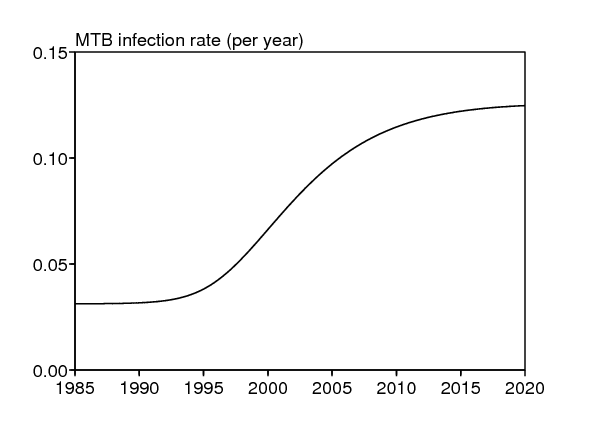
    Le paramètre \(p_2\,\) pour la progression rapide vers la tuberculose chez les personnes séropositives. (Di Perri et coll., 1989) a étudié une épidémie de tuberculose parmi des personnes séropositives: après le premier cas, huit personnes ont développé la tuberculose rapidement et six avaient un nouveau test tuberculinique positif, ce qui suggère que \(\,8/14\simeq 57\%\,\) des personnes séropositives nouvellement infectées développent une tuberculose primaire. En 1992, (Daley et coll., 1992) a étudié une épidémie semblable et a trouvé une proportion égale à \(11/15\simeq 73\%\). Mais il est possible que seules les épidémies importantes soient étudiées et que les épidémies avec moins de cas de tuberculose primaire ne soient pas remarquées ou ne soient pas un bon sujet de publication. Un biais similaire se serait produit si l'on avait basé notre estimation de la probabilité d'une progression rapide parmi les personnes séronégatives sur des rapports d'épidémies tels que (Kline et coll., 1995), qui indique \(14/41=34\%\,\) de tuberculose primaire. Par conséquent, on préfère faire varier \(p_2\) pour ajuster les données concernant le taux de notification dans le tableau 4. Dans ce but, on a simulé le système (1)-(6) en partant de la condition initiale \[S_1(t_0)=S_1^*\, ,\quad E_1(t_0)=E_1^*\, ,\quad I_1(t_0)=I_1^*\, ,\quad S_2(t_0)=1\, ,\quad E_2(t_0)=I_2(t_0)=0\, .\] Noter à ce stade que tous les paramètres du tableau 1 ont été fixés, sauf \(p_2\). L'ajustement donne \(\,p_2=30\%\) (ligne continue de la figure 2a), soit presque 3 fois la valeur \(p_1\,\) pour les personnes séronégatives. Noter que cette valeur pour \(\,p_2\,\) est encore inférieure à celles obtenues par l'étude d'épidémies de tuberculose parmi les personnes séropositives (Daley et coll., 1992 ; Di Perri, 1989). Vue la mortalité \(\,\mu_2\,\) des personnes séropositives, les estimations pour \(a_2\) et \(p_2\) correspondent à une probabilité de progresser lentement de la tuberculose latente à la tuberculose active \[a_2/(a_2+\mu_2)\simeq 44\%\] et à une probabilité de développer une tuberculose active après une infection avec M. tuberculosis \[p_2+a_2/(a_2+\mu_2)\simeq 74\%\, .\] En comparaison, le pourcentage de personnes séropositives qui progressent rapidement (soit immédiatement soit avant un an) vers la tuberculose active était de 20% dans (Guwatudde et coll., 2004) (sans référence), 42% dans (Schulzer et coll., 1992) (sans référence), 67% dans (Cohen et coll., 2006) (d'après (Daley et coll., 1992)) et 100% dans (West et Thompson, 1997). Dans les modèles avec un compartiment séparé pour le SIDA tels que (Dowdy et coll., 2006), le pourcentage était de 7% pour les personnes séropositives sans SIDA (le même que pour les personnes séronégatives) et 56% avec le SIDA, selon (Daley et coll., 1992 ; Di Perri, 1989).

\((a)\)	\((b)\)
\((c)\)	\((d)\)

    Toutes les valeurs des paramètres ont été fixées et sont présentées dans le tableau 6.

    Le pourcentage de notifications de la tuberculose qui sont séropositives. La ligne en pointillé dans la figure 2a montre la contribution des personnes séropositives au taux de notification de la tuberculose, produite par simulation du modèle complet (1)-(6) avec les paramètres du tableau 6. La courbe passe près de la seule donnée dont on dispose (66% de personnes séropositives parmi les cas notifiés de tuberculose en 2005 (Wood et coll., 2007)). Ceci suggère que nos estimations de paramètres ne sont pas déraisonnables.

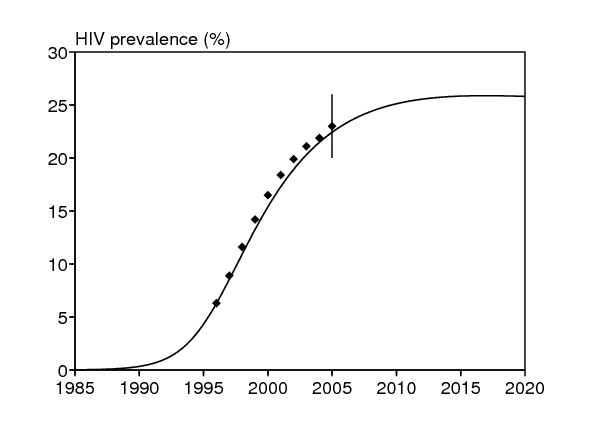
    Vérification de l'hypothèse utilisée pour estimer les paramètres pour le VIH \(d\), \(\lambda\) et \(t_0\). On peut vérifier s'il était raisonnable de négliger les termes comprenant \(I_1\) et \(I_2\,\) dans (24)-(25). La figure 2b montre en effet que la simulation du modèle complet (1)-(6) avec les paramètres du tableau 6 s'ajuste toujours bien aux données sur le VIH. Noter que la donnée avec un intervalle de confiance binômial à 95% dans la figure 2b correspond à la prévalence de 23% (174/762) du VIH dans l'échantillon de la population pris en 2005 (Wood et coll., 2007).

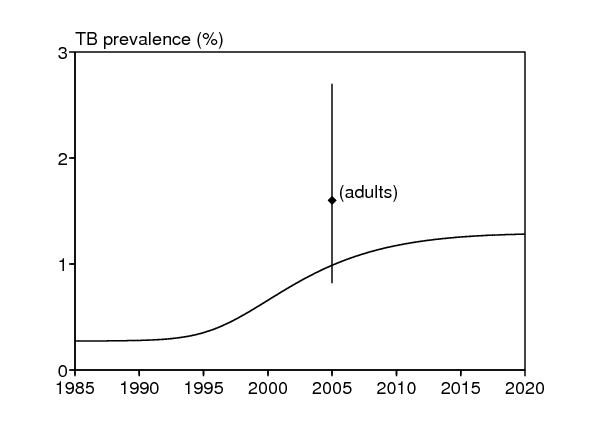
    Autres courbes. La figure 2c montre la prévalence de la tuberculose non diagnostiquée, calculée en simulant le modèle complet (1)-(6) avec les paramètres du tableau 6. La donnée avec un intervalle de confiance binômial à 95% correspond à la prévalence de la tuberculose non diagnostiquée parmi les adultes (12/762), qui doit être supérieure à celle dans la population entière. Ainsi la figure 2c suggère aussi que nos estimations pour les paramètres ne sont pas déraisonnables. Enfin on montre aussi le taux d'infection par M. tuberculosis (figure 2d), sur lequel des données ont été collectées récemment mais pas encore publiées. Rappelons cependant que nos choix pour les taux de détection de la tuberculose, \(\,\gamma_1\) et \(\gamma_2\), étaient influencés par la connaissance du fait que taux d'infection n'avait pas crû aussi vite que le taux de notification.

7.   Sensibilité des états d'équilibre par rapport aux valeurs des paramètres

    Tous les paramètres ayant été fixés ou estimés (tableau 6), on observe les résultats numériques donnés par les formules mathématiques de la section 4 pour les états d'équilibre. Tout d'abord, l'état d'équilibre sans VIH et sans tuberculose est \(S_1^0=10\,000\). On obtient aussi \[R_0^{\mathrm{TB}}\simeq \mbox{1,3}\, ,\quad R_0^{\mathrm{VIH}}\simeq \mbox{7,0}\, ,\quad r_0^{\mathrm{TB}}\simeq \mbox{1,7}\, ,\quad r_0^{\mathrm{VIH}}\simeq \mbox{5,8}\, .\] L'estimation \(R_0^{\mathrm{TB}}\simeq \mbox{1,3}\,\) est proche de l'intervalle [0,6 1,2] mentionnée dans (Murray et coll., 1990). Avec les données nationales de prévalence du VIH dans les cliniques prénatales, (Williams et Gouws, 2001 ; Williams et coll., 2006) ont trouvé un résultat semblable \(\,R_0^{\mathrm{VIH}}\simeq \mbox{6,4}\pm \mbox{1,6}\). Noter aussi \(r_0^{\mathrm{TB}} > R_0^{\mathrm{TB}}\) : une personne « moyenne » nouvellement infectée par M. tuberculosis produit plus de cas secondaires si elle est introduite dans une population sans tuberculose où le VIH est endémique que si elle est introduite dans une population complètement saine. C'est parce que cette personne « moyenne » est probablement séropositive, donc la probabilité de progresser vers une tuberculose active et d'infecter d'autres personnes est élevée (cela dépend des valeurs numériques de plusieurs paramètres, y compris \(\,a_2\), mais pas de la structure du modèle). Enfin, \(\,r_0^{\mathrm{VIH}} < R_0^{\mathrm{HIV}}\), comme cela est expliqué dans le §4.3. D'une certaine manière, on peut dire que la tuberculose ralentit l'épidémie de VIH.

    Dans les sections suivantes, on étudie la sensibilité des différents états d'équilibre par rapport aux paramètres les plus importants du modèle, à savoir ceux qui entrent dans les termes non linéaires du système (1)-(6): les taux de transmission de la tuberculose \(k_1\) et \(k_2\), les paramètres de réinfection \(q_1\) et \(q_2\,\), et les paramètres \(d\) et \(\lambda\) pour le VIH.

7.1   Vue globale des états d'équilibre dans le diagramme \((k_1,d)\)

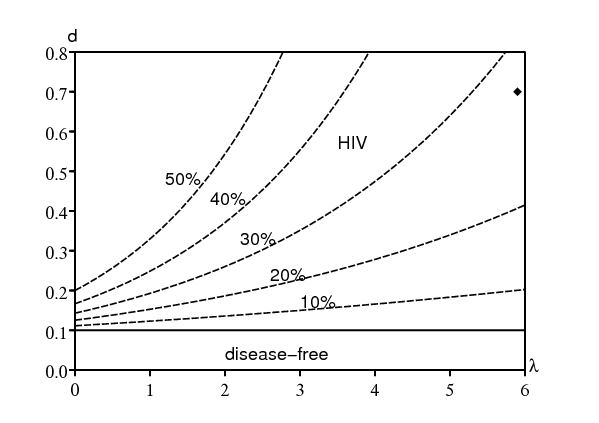
    La figure 3 montre un diagramme de bifurcation des états d'équilibre dans l'espace des paramètres \((k_1,d)\) en utilisant les valeurs numériques du tableau 6, sauf bien sûr pour \(k_1\,\) et d, et avec un quotient constant \(\,k_2/k_1\). Le point noir près de la ligne 2000 pour le taux de notification de la tuberculose (pour 100000 par an) correspond aux valeurs de \(\,k_1\) et d dans le tableau 6. Les limites entre les quatre domaines du diagramme de bifurcation (« sans maladie », « VIH », « tuberculose » et « VIH+tuberculose ») s'obtiennent en résolvant les quatre équations \(\,R_0^{\mathrm{VIH}}=1\), \(r_0^{\mathrm{VIH}}=1\), \(R_0^{\mathrm{TB}}=1\) et \(r_0^{\mathrm{TB}}=1\) en fonction de \(k_1\,\) et d. \(R_0^{\mathrm{VIH}}\) ne dépend pas de \(k_1\) et \(R_0^{\mathrm{TB}}\,\) ne dépend pas de d. Donc la ligne \(R_0^{\mathrm{VIH}}=1\) est horizontale et la ligne \(R_0^{\mathrm{TB}}=1\,\) est verticale. La ligne \(\,r_0^{\mathrm{VIH}}=1\,\) sépare les domaines « tuberculose » et « VIH+tuberculose ». La ligne \(\,r_0^{\mathrm{TB}}=1\) sépare les domaines « VIH » et « VIH+tuberculose ».

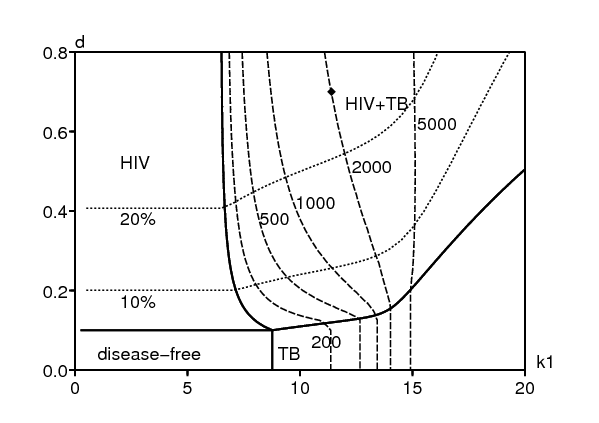
    Noter dans la figure 3 comment les lignes de niveau pour le taux de notification de la tuberculose sont tordues lorsqu'elles traversent la ligne \(r_0^{\mathrm{VIH}}=1\,\) de la zone « tuberculose » vers la zone « VIH+tuberculose ». Les taux de notification proches du « seuil de réinfection » mentionné dans la section 4.1 (par exemple les lignes de niveau 1000 et 2000), qui semblaient tout à fait irréalistes en l'absence du VIH, se produisent maintenant pour des valeurs plus petites du taux de transmission \(k_1\,\) si la prévalence du VIH est assez élevée. Avec \(k_1=\mbox{11,4}\) par an comme dans le tableau 6, le taux de notification de la tuberculose à l'état d'équilibre croît de 200 à 2000 pour 100000 par an, à mesure que la prévalence du VIH croît de 0 à environ 25%.

7.2   L'état d'équilibre avec la tuberculose mais sans VIH

    L'état d'équilibre avec la tuberculose mais sans VIH est indiqué dans le côté gauche du tableau 7. C'est l'équilibre utilisé comme condition initiale dans les simulations du modèle complet avec à la fois le VIH et la tuberculose. Noter que le « quotient de Styblo » (à la fois pour les cas à frottis positif et ceux à frottis négatif) est environ de 100, la valeur communément admise pour les populations séronégatives.

    La figure 4 montre comment l'état d'équilibre avec la tuberculose seule change si l'on modifie \(k_1\) et \(q_1\). Elle montre aussi les lignes de niveau du taux de notification de la tuberculose. Le point noir sur la ligne de niveau 200 pour 100000 par an correspond aux valeurs numériques de \(\,k_1\) et \(q_1\) dans le tableau 6. Une figure semblable, tracée à la main et sans les lignes de niveau, se trouve dans (Feng et coll., 2000, figure 3). Certaines lignes se croisent dans la zone de la figure 4 avec deux solutions positives. Ce sont les projections sur le plan de lignes tracées sur une surface en dimension 3 avec un pli.

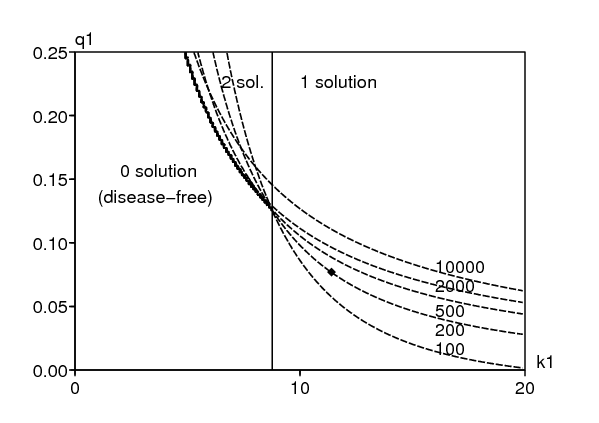
    Numériquement, le seuil au-dessus duquel deux équilibres non triviaux peuvent exister est \(q_1^*\simeq \mbox{12,5}\%\), alors qu'on a choisi \(q_1=\mbox{7,7}\%\). L'autre seuil, qui sépare la zone où il y a 0 ou 2 solutions non triviales de la zone où il n'y a qu'une solution, est \(\,k_1^*\simeq \mbox{8,8}\) par an, alors qu'on a choisi \(k_1=\mbox{11,4}\,\) par an. Les courbes de niveau dans la figure 4 montrent que le taux de notification de la tuberculose à l'équilibre est sensible aux variations de \(\,q_1\). Ceci signifie que notre estimation dans la section 6 du paramètre \(\,k_1\) doit être considérée avec précaution.

    Comme l'ont remarqué (Gomes et coll., 2004 ; Singer et Kirschner, 2004) pour un modèle légèrement différent, la dépendance du taux de notification de la tuberculose par rapport à \(q_1\,\) est encore plus grande au-dessus d'un certain « seuil de réinfection ». Voir les remarques à la fin de l'appendice et (Breban et Blower, 2005 ; Gomes et coll., 2005) pour une discussion au sujet de cette terminologie. Noter par exemple la proximité entre les lignes de niveau 2000 et 10000 dans la figure 4. Cependant, des taux de notification proches de 2000 pour 100000 par an comme dans le bidonville de notre étude (avec le VIH) sont déjà parmi les plus élevés jamais rapportés dans une communauté. Donc il semble improbable que les valeurs des paramètres pour la tuberculose dans une communauté sans VIH soient au-dessus du « seuil de réinfection », comme suggéré dans (Gomes et coll., 2004 ; Singer et Kirschner, 2004).

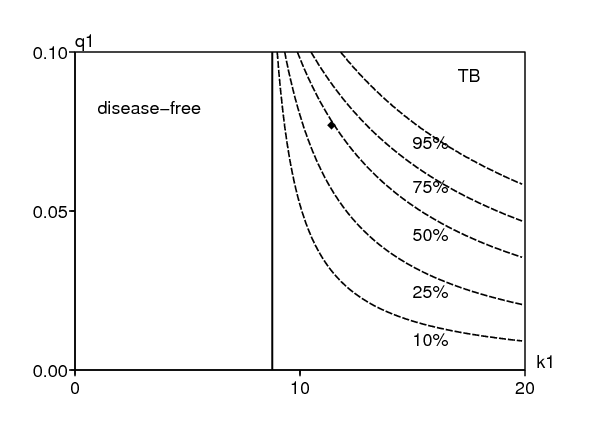
    La figure 5 montre le pourcentage des nouveaux cas de tuberculose dûs à une réinfection en fonction de \(k_1\) et \(q_1\). Noter que l'échelle verticale n'est pas la même que dans la figure 4. Un point noir indique les valeurs numériques de \(k_1\) et \(q_1\,\) du tableau 6 ; il correspond à 45% de réinfection parmi les nouveaux cas de tuberculose.

7.3   L'état d'équilibre avec VIH mais sans tuberculose

    Dans notre modèle, l'état d'équilibre avec VIH mais sans tuberculose est donné par \(\widehat{S}_1\simeq 3\,450\), \(\widehat{S}_2\simeq 1\,310\) et \(\widehat{H}\simeq 28\%\). La population totale à l'équilibre avec le VIH est inférieure à la moitié de l'équilibre sans maladie \(S_1^0\), car on considère des cohortes de B naissances par an et non la population totale réelle avec ses entrées et sorties. La figure 6 montre la sensibilité de la prévalence à l'équilibre du VIH par rapport aux variations de λ et d. Le point noir dans le coin en haut à droite correspond aux valeurs numériques de λ et de d dans le tableau 6.

7.4   L'état d'équilibre avec à la fois le VIH et la tuberculose

    L'état d'équilibre endémique avec à la fois le VIH et la tuberculose peut être calculé numériquement. Le tableau 7 en montre les caractérictiques. Ce sont celles qui auraient été obtenues si on avait continué les simulations de la figure 2 jusqu'à atteindre un équilibre. Comparé avec l'état d'équilibre endémique avec la tuberculose seule (côté gauche du tableau 7), le taux de notification de la tuberculose et l'incidence de la tuberculose ont été multipliés par 10, la prévalence de la tuberculose et le taux d'infection par 4. La prévalence de M. tuberculosis n'a que légèrement augmenté. La réactivation est devenue la voie de progression vers la tuberculose active la plus importante. La figure 3 a déjà montré la sensibilité de l'état d'équilibre VIH-tuberculose.

    L'épidémie de tuberculose associée au VIH conduit-elle à un risque accru d'infection par la tuberculose dans la population, en particulier chez les personnes séronégatives ? Cette question fait l'objet de débats dans la littérature médicale (Egwaga et coll., 2006 ; Lawn et Wood, 2006a ; Williams et Maher, 2007). (Egwaga et coll., 2006) a trouvé que le risque d'infection avait baissé entre 1983 et 2003 en Tanzanie chez les enfants âgés de 6 à 14 ans malgré l'accroissement dans la population de l'incidence de la tuberculose liée au VIH. De même, (Corbett et coll., 2003a) n'a pas trouvé d'accroissement de l'incidence de la tuberculose chez des mineurs sud-africains séronégatifs. Au contraire, (Lawn et Wood, 2006a) a remarqué que dans le bidonville sud-africain qui est l'objet de notre étude, le taux de notification de la tuberculose chez les adolescents séronégatifs avaient considérablement augmenté ces dernières années; donc le risque d'infection a probablement aussi augmenté. C'est ce qui se passe dans notre modèle: le taux d'infection par M. tuberculosis est multiplié par 4 à mesure que la prévalence du VIH croît de 0 à son équilibre de 24%.

8.   Mesures de contrôle

8.1   Usage des préservatifs

    Noter avec (20)-(21)

• \(r_0^{\mathrm{VIH}}\) est proportionnel à \(f(0)=d\) (le taux maximum de transmission du VIH)
• \(r_0^{\mathrm{TB}}\) est proportionnel à \(k_1\) (le taux maximum de transmission de la tuberculose), avec un quotient constant \(\,k_2/k_1\).

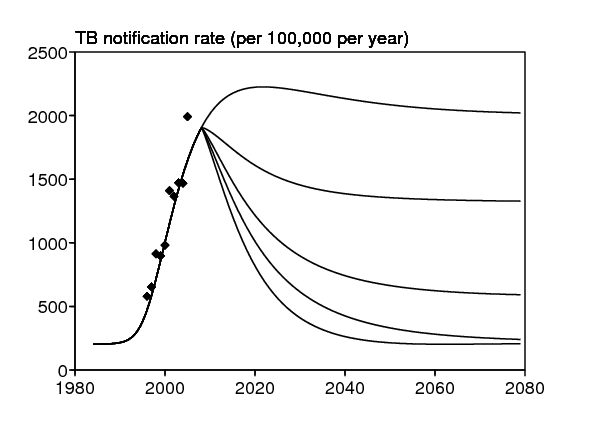
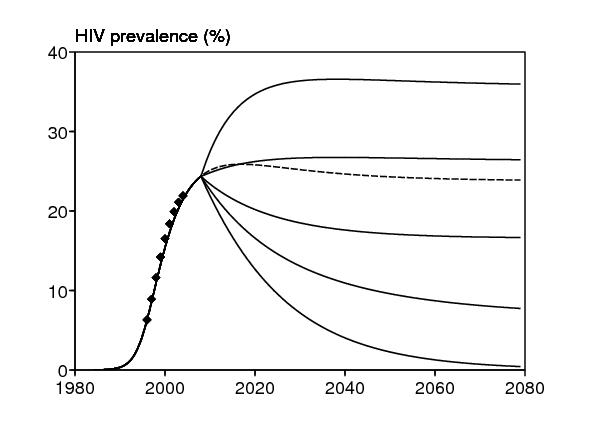
    La figure 7 montre l'impact d'une baisse soudaine du taux de transmission du VIH, d'une valeur initiale d jusqu'à une nouvelle valeur \(\,d'\,\), sur la prévalence du VIH (figure 7b) et aussi indirectement sur le taux de notification de la tuberculose (figure 7a). L'impact est une fonction monotone de \(\,d'\,\), comme on pourrait s'y attendre. On peut vérifier sur ces simulations que le VIH ne disparaît à long terme que si \(\,d' < d/r_0^{\mathrm{VIH}}\simeq d/\mbox{5,8}\,\), c'est-à-dire dans les deux simulations \(d'=d/8\) et \(d'=0\) mais pas si \(d'=d\), \(d'=d/2\) ou \(d'=d/4\). Dans le premier cas, le taux de notification de la tuberculose retourne finalement à son niveau du début des années 1980, avant l'introduction du VIH. Le comportement asymptotique du taux de notification de la tuberculose et de la prévalence du VIH peut aussi se lire directement sur les lignes de niveau de la figure 3. Mais la vitesse à laquelle ces état d'équilibre sont atteints ne se voit que sur la figure 7.

\((a)\)	\((b)\)

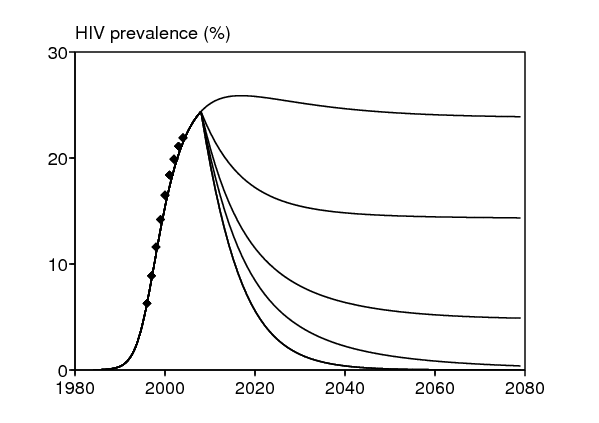    En l'absence d'intervention (figure 7, \(d'=d\)), noter dans la simulation que le pic pour la prévalence du VIH se produit à peu près en même temps que le pic pour le taux de notification de la tuberculose. Cela ne semble pas incompatible avec les données du Kenya (Currie et coll., 2005, figure 1), qui suggèrent un retard de plusieurs années entre la montée du VIH et celle de la tuberculose. Une raison pour un tel retard pourrait être que les cas de tuberculose active apparaissent avec une plus grande fréquence aux phases avancées de l'infection par le VIH. Les données du bidonville sud-africain ne montrent cependant aucun retard évident. Notre modèle avec seulement deux compartiments pour le VIH (séronégatif / séropositif) s'ajuste assez bien aux données pour la tuberculose et le VIH bien qu'il ne contienne pas de retard. Les contextes au Kenya et dans le bidonville sud-africain sont probablement assez différents puisque pour des prévalences du VIH similaires, le taux de notification de la tuberculose au Kenya n'est qu'un tiers de celui dans le bidonville sud-africain.

    Enfin, il faut mentionner qu'une campagne de promotion de grande ampleur pour l'utilisation des préservatifs a commencé à la télévision à la fin de 2006 en Afrique du Sud. En principe, il devrait être possible de récupérer des données concernant le nombre de préservatifs achetés par la population du bidonville et vérifier si les comportements ont changé.

8.2   Détection de la tuberculose

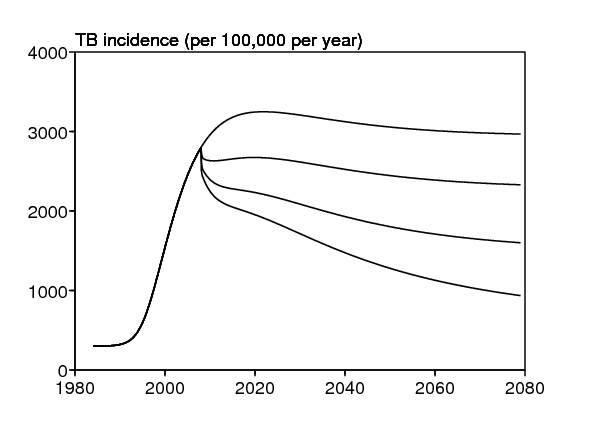
    On considère maintenant la possibilité d'accroître les taux de détection de la tuberculose (\(\gamma_1\) et \(\gamma_2\)) et les probabilités de succès d'un traitement (\(\varepsilon_1\) et \(\varepsilon_2\)). Pour le bidonville, on pourrait y parvenir en cherchant activement les cas de tuberculose plutôt que d'attendre qu'ils viennent à la clinique. Les quatre paramètres ci-dessus n'entrent dans le système d'équations différentielles (1)-(6) qu'à travers les combinaisons \(\,b_1=\beta_1+\gamma_1\, \varepsilon_1\) et \(b_2=\beta_2+\gamma_2\, \varepsilon_2\). Il faut cependant faire un peu attention parce que \(\,\gamma_1\) et \(\gamma_2\,\) entrent dans l'expression du taux de notification de la tuberculose (\(\gamma_1\, I_1+\gamma_2\, I_2\)). Si l'on augmente \(\,\gamma_1\) ou \(\gamma_2\,\), le taux de notification de la tuberculose à l'équilibre peut augmenter et ne commencer à baisser que si \(\gamma_1\) ou \(\gamma_2\,\) est assez grand. Il n'est pas convenable de prendre le taux de notification de la tuberculose comme mesure de la sévérité de la situation lorsque le taux de détection change. À la place, on utilisera le taux d'incidence de la tuberculose.

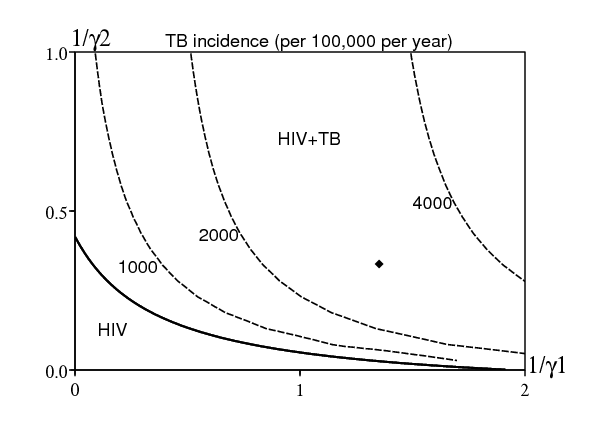
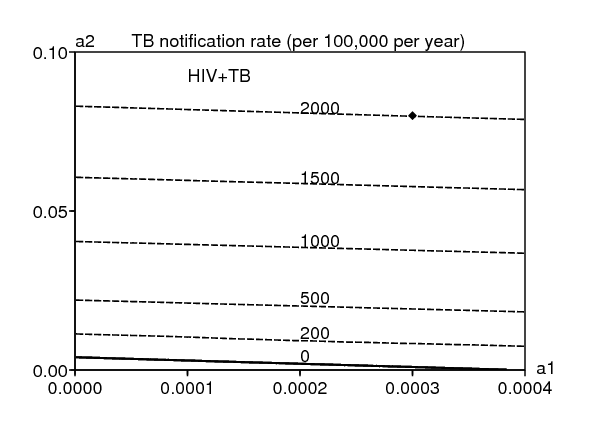
    La figure 8a montre le diagramme de bifurcation et les lignes de niveau du taux d'incidence de la tuberculose dans l'espace des paramètres \((1/\gamma_1,1/\gamma_2)\,\), avec les valeurs numériques du tableau 6 pour les autres paramètres. \(\gamma_1\) et \(\gamma_2\) n'interviennent pas dans la formule pour \(R_0^{\mathrm{VIH}}\). L'état d'équilibre avec le VIH endémique est donc toujours là. Cet état d'équilibre peut-il être envahi par la tuberculose? La réponse est donnée par l'équation \(\,r_0^{\mathrm{TB}}=1\), une équation implicite pour \(\gamma_1\) et \(\gamma_2\,\) représentée par une épaisse ligne noire qui sépare « VIH » de « VIH+tuberculose » dans le coin en bas à gauche de la figure 8a. Les valeurs de \(\,\gamma_1\) et \(\gamma_2\) dans le tableau 6 correspondent au point noir dans la figure.

    La figure 8b montre l'impact d'un accroissement soudain du taux de détection de la tuberculose \(\gamma_2\,\) pour les personnes séropositives. Ceci n'a presque aucun impact sur la courbe pour la prévalence du VIH. On ne la montre donc pas. Bien sûr, l'incidence de la tuberculose décroît de manière monotone à mesure que croît le taux de détection.

\((a)\)	\((b)\)

8.3   Traitement prophylactique avec l'isoniazide

    Ce traitement réduit

• \(a_1\) s'il est appliqué aux personnes séronégatives
• \(a_2\) s'il est appliqué aux personnes séropositives.

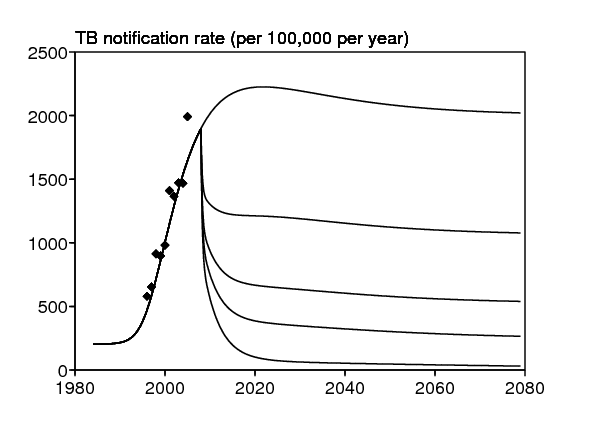
    La figure 9b montre l'influence d'une baisse soudaine du taux de progression \(a_2\,\) pour les personnes séropositives due à un traitement prophylactique avec l'isoniazide. Cela n'a presque pas d'influence sur la courbe de prévalence du VIH; on ne la montre donc pas. Le taux de notification de la tuberculose à l'équilibre décroît de manière monotone quand \(\,a_2\) décroît.

\((a)\)	\((b)\)

8.4   Antirétroviraux

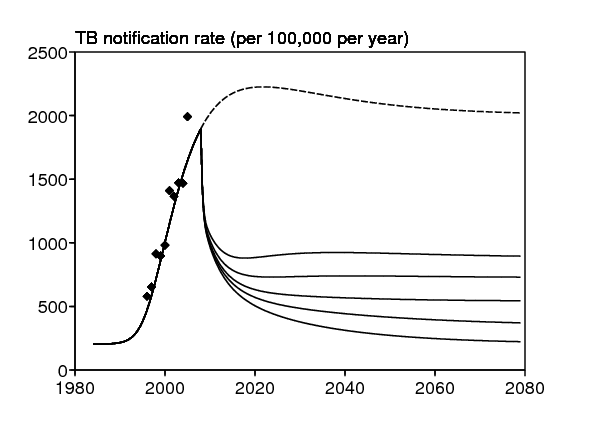
    On considère maintenant l'impact possible des traitements antirétroviraux, plus exactement des trithérapies. Ils réduisent la charge virale et donc aussi le paramètre de transmission d pour le VIH. Mais ils augmentent aussi l'espérance de vie des personnes séropositives en abaissant \(\mu_2\) et \(m_2\) (bien sûr pas en dessous de la mortalité naturelle \(\mu_1\)), ce qui augmente le nombre de personnes vivant avec le VIH et favorise la transmission du VIH. Ces deux effets s'opposent. L'impact sur le VIH au niveau de la population n'est donc pas évident et dépend de l'amplitude avec laquelle les trois paramètres changent sous l'effet des antirétroviraux. Les antirétroviraux réduisent par ailleurs en moyenne le taux auquel les personnes coinfectées développent une tuberculose active, mais pas au même niveau que les personnes séronégatives infectées par la tuberculose (Badri et coll., 2002 ; Wilson ; Lawn et coll., 2005a et 2005b ; Lawn et Wood, 2006b), et même si une maladie de « reconstitution immunitaire » peut au contraire augmenter \(\,a_2\,\) pendant les premiers mois de traitement antirétroviral (Lawn et coll., 2008). À nouveau, l'effet des antirétroviraux sur la tuberculose n'est pas évident car les personnes séropositives sous antirétroviraux vivent plus longtemps. Quantitativement, des études en Afrique du Sud (Badri et coll., 2002 ; Lawn et coll., 2005b) et au Brésil (Miranda et coll., 2007) ont montré que les antirétroviraux réduisent de 80% \(a_2\), c'est-à-dire qu'ils divisent \(a_2\) par 5. Avec \(a_2=\mbox{0,08}\) par an sans antirétroviraux, cela donne \(a_2=\mbox{0,016}\,\) par an avec les antirétroviraux. C'est encore 50 fois plus que \(\,a_1=\mbox{0,0003}\,\) par an pour les personnes séronégatives. Un autre rapport (Lawn et coll., 2006) mentionne un risque 5 à 10 fois supérieur après trois ans d'antirétroviraux par rapport aux personnes séronégatives. On suppose de plus que

• \(\mu_2\) est divisé par 2 sous l'effet des antirétroviraux, ce qui donne \(\mu_2=\mbox{0,05}\) par an au lieu de \(\mbox{0,1}\) par an, toujours au-dessus de la mortalité naturelle \(\mu_1=\mbox{0,02}\,\) par an; la nouvelle espérance de vie pour les personnes séropositives sous antirétroviraux est 20 ans;
• \(m_2\) est divisé par 2 sous l'effet des antirétroviraux : \(m_2=\mbox{0,8}\) par an, alors que \(m_1=\mbox{0,25}\) par an.

\((a)\)	\((b)\)

    Les antirétroviraux sont de plus en plus disponibles dans le bidonville depuis 2006. Mais il est encore trop tôt pour comprendre quel a été son impact sur les épidémies de VIH et de tuberculose.

9.   Conclusion

    Ce travail est une première tentative pour modéliser les épidémies simultanées de VIH et de tuberculose dans un bidonville près du Cap en Afrique du Sud, pour lequel beaucoup de données sont disponibles. La difficulté principale vient du grand nombre de paramètres dans le modèle, ce qui rend difficile les estimations et l'analyse mathématique. On a fait en sorte que ce nombre soit aussi petit que possible; on a ainsi pu faire une étude relativement complète du modèle avec le VIH seul ou la tuberculose seule.

    On a montré que la bifurcation sous-critique dans notre modèle avec la tuberculose seule était impossible avec des valeurs réalistes des paramètres car M. tuberculosis donne un certain degré de protection contre une progression rapide vers la tuberculose active après réinfection (\(q_1\leq p_1\)). À notre connaissance, aucun modèle pour la tuberculose n'a jamais présenté de bifurcation sous-critique avec des valeurs réalistes des paramètres, malgré toute l'emphase mise sur cette possibilité dans les articles mathématiques sur la tuberculose (Feng et coll., 2000 ; Moghadas et Alexander, 2004 ; Sharomi et coll., 2008). Sur ce point, on est d'accord avec (Lipsitch et Murray, 2003) et (Singer et Kirschner, 2004).

    Quant au modèle complet (1)-(6) avec à la fois le VIH et la tuberculose, on a étudié la stabilité linéaire de l'équilibre endémique avec la tuberculose ou le VIH. Dans le cas \(q_1\leq p_1\), on a conjecturé qu'il n'y avait pas de bifurcation sous-critique pour (1)-(6). Ce point reste néanmoins à vérifier mathématiquement. On a tracé des diagrammes de bifurcation avec des lignes de niveau pour la prévalence du VIH et le taux de notification de la tuberculose. Le diagramme le plus intéressant se trouve dans la figure 3. Il montre comment, pour une valeur fixée du taux de transmission de la tuberculose, le taux de notification de la tuberculose à l'état d'équilibre peut croître de 200 à 2000 pour 100000 par an quand la prévalence du VIH croît de 0 à environ 25%.

    (Gomes et coll., 2004 ; Gomes et coll., 2005 ; Gomes et coll., 2007) ont insisté sur le rôle du « seuil de réinfection » dans les modèles de tuberculose sans VIH. Dans (Gomes et coll., 2004, figure 3) et (Gomes et coll., 2007, figure 2), ce seuil était atteint lorsqu'environ 1% de la population avait une tuberculose active. Dans le bidonville sud-africain, 12/762≈1,6% d'un échantillon de la population avait une tuberculose active non diagnostiquée en 2005. Ceci pourrait suggérer qu'il y a effectivement des populations qui se trouve au-delà du « seuil de réinfection ». Cependant, on peut se demander si des populations avec une tuberculose endémique mais une faible prévalence du VIH peuvent réellement atteindre 1% de prévalence pour la tuberculose active. Autrement dit, on peut se demander si de telles populations ne sont pas systématiquement sous le « seuil de réinfection », et si ce seuil peut toujours être utilisé pour expliquer certains problèmes dans l'épidémiologie de la tuberculose tels que l'inefficacité du vaccin BCG (Gomes et coll., 2004).

    Même dans les populations avec une prévalence du VIH élevée, le « seuil de réinfection » ne semble pas jouer un rôle important. Le tableau 7 suggère que le pourcentage de réinfection avec le VIH et la tuberculose est inférieur à celui lorsque la tuberculose est seule.

    Parmi les interventions que l'on a étudiées, la plupart ont un impact positif évident pour limiter les épidémies de VIH et de tuberculose: c'est le cas pour l'utilisation de préservatifs, la détection de la tuberculose et le traitement prophylactique. La situation pour les antirétroviraux est plus compliquée. Cependant, bien que l'avenir pour la prévalence du VIH soit incertain, il semblerait qu'un accès généralisé aux antirétroviraux conduirait à une baisse significative du taux de notification de la tuberculose. En effet, on sait d'après des études menées en Afrique du Sud et au Brésil que les antirétroviraux peuvent réduire le taux de progression de la tuberculose latente vers la tuberculose active d'environ 80%, soit une division par 5. Si les personnes séropositives sous antirétroviraux vivent environ 2 fois plus longtemps que les 10 années de survie moyenne des personnes séropositives sans accès aux antirétroviraux, alors on s'attend à ce que l'incidence de la tuberculose soit multipliée par 2/5. C'est une réduction de 60%.

    Ce simple argument peut être faux si les antirétroviraux augmentent la prévalence du VIH et indirectement l'incidence de la tuberculose. Nos résultats numériques suggèrent que tel n'est pas le cas. Même dans le pire scénario où la prévalence du VIH augmente à cause de l'introduction des antirétroviraux (ligne continue du haut de la figure 10b), le taux de notification de la tuberculose baisse considérablement (ligne continue en haut de la figure 10a).

    Il est difficile de dire si les observations tirées de ce modèle avec des paramètres adaptés à ce bidonville sud-africain valent pour des régions moins denses avec une prévalence du VIH élevée. On pourrait essayer d'utiliser le même modèle et adapter les paramètres aux données locales. Malheureusement, les données fiables à la fois sur le VIH et la tuberculose sont rares. Par exemple, la prévalence du VIH au Zimbabwe n'a probablement pas été estimée aussi régulièrement que (Hughes et coll., 2006, figure 5) pourrait le suggérer [J. Hargrove, communication personnelle].

Preuve annexe

    \(i_1^+\) et \(i_1^-\,\) sont les deux racines éventuellement complexes de l'équation (13), de la forme \begin{equation}\tag{26} \bigl (i_1^*\bigr )^2 + c_1\, i_1^* + c_0=0\, . \end{equation} On ne s'intéresse qu'aux racines positives, les seules avec une signification biologique. L'existence de racines positives dépend en particulier des signes des coefficients de (26). On doit distinguer plusieurs cas:

• Le cas où \(k_1 > k_1^*\). Parce que \(\,c_0 < 0\), on a \(i_1^+ \times i_1^- < 0\). Ceci ne se produit que si \(\,i_1^+ > 0\) et \(i_1^- < 0\). Il n'y a donc qu'une seule racine positive de (13).
• Le cas où \(0 < k_1 < k_1^*\) et \(0 < k_1 < \widetilde{k}_1(q_1)\), avec \begin{equation}\tag{27} \widetilde{k}_1(q_1)=\frac{a_1+b_1+(1-p_1)\, m_1+p_1 \mu_1}{q_1} + m_1\, . \end{equation} Dans ce cas, on a \(c_1 > 0\). On a donc \(\,i_1^+ + i_1^- < 0\). Mais \(\,i_1^+ \times i_1^- > 0\). Donc ce cas ne se produit que si \(i_1^+\) et \(i_1^-\) sont tous les deux négatifs ou si \(i_1^+\) et \(i_1^-\,\) sont des nombres complexes conjugués dont la partie réelle est négative. Donc il n'y a pas de racine positive de (13). Noter que \(\,\widetilde{k}_1(q_1) < k_1^*\) uniquement lorsque \(q_1 > q_1^*\), la définition (17) de \(q_1^*\) ayant été choisie précisément dans ce but.
• Le cas où \(0 < k_1 < k_1^*\) et \(k_1 > \widetilde{k}_1(q_1)\) (qui implique que \(q_1 > q_1^*\)). Δ est le discriminant de (13). Insistons sur la dépendance par rapport à un paramètre en écrivant \(\,\Delta(k_1)\). Avec (13), \(\,\Delta(k_1)\,\) est un polynôme quadratique en \(1/k_1\), donc l'équation \(\Delta(k_1)=0\) a au plus deux racines dans la demi-droite \(k_1 > 0\). On a
  • \(\Delta(k_1)=c_1^2-4\, c_0\),
  • \(c_1=0\) si \(k_1=\widetilde{k}_1(q_1)\)
  • \(c_0=0\) si \(k_1=k_1^*\).
  On a \(\,\Delta(\widetilde{k}_1(q_1)) < 0\) et \(\Delta(k_1^*) > 0\). Donc l'équation \(\,\Delta(k_1)=0\) a au moins une racine dans l'intervalle \(]\widetilde{k}_1(q_1),k_1^*[\,\). L'équation ne peut pas avoir deux racines parce que la fonction \(\,k_1\mapsto \Delta(k_1)\,\) doit changer de signe un nombre impair de fois dans cet intervalle. On définit \(\,\widehat{k}_1(q_1)\), l'unique racine. On a alors \(\,\Delta(k_1) < 0\) si \(\widetilde{k}_1(q_1) < k_1 < \widehat{k}_1(q_1)\) : dans ce cas, l'équation (13) n'a pas de solution parmi les nombres réels. Dans le cas \(\,\widehat{k}_1(q_1) < k_1 < k_1^*\), on a \(\Delta(k_1) > 0\), \(c_0=i_1^+ \times i_1^- > 0\), et \(c_1=-(i_1^++i_1^-) < 0\) : dans ce cas, l'équation (13) a deux solutions positives.

    On doit encore vérifier que si (13) a une racine positive \(i_1^*\), alors toutes les composantes du triplet \((S_1^*,E_1^*,I_1^*)\,\) donné par (14)-(15) sont positives. Pour cela, il suffit de montrer que \(s_1^* > 0\) et \(e_1^* > 0\). Mais en additionnant (8) et (9), on trouve \(\,s_1^*=(\mu_1 e_1^*+m_1 i_1^*)/(k_1 i_1^*)\). Donc il suffit de montrer \(\,e_1^* > 0\), c'est-à-dire \(i_1^* < 1-m_1/k_1\). Noter tout d'abord avec (27) que si (13) a une racine positive \(i_1^*\,\), alors on a nécessairement \(k_1 > m_1\). On définit \(\,\chi(i_1)\,\), le polynôme quadratique du côté gauche de (13), de sorte que \(\chi(i_1^*)=0\). Des calculs simples montrent \begin{align*} \chi(1-m_1/k_1)&=\frac{[b_1+(1-p_1)\, m_1]\, (k_1-m_1+\mu_1)}{q_1 k_1^2} > 0\, ,\\ \chi'(1-m_1/k_1)&=1-\frac{m_1}{k_1} + \frac{a_1+b_1+(1-p_1) m_1+p_1 \mu_1}{q_1 k_1} > 0\, , \end{align*} ce qui implique que \(i_1^* < 1-m_1/k_1\). Ceci termine la preuve.

    Pour terminer, voici quelques remarques sur la notion de « seuil de réinfection » (Breban et Blower, 2005 ; Gomes et coll., 2004 ; Gomes et coll., 2005) pour notre modèle dans le cas où \(k_1 > k_1^*\). C'est équivalent à \(R_0^{\mathrm{TB}} > 1\) et aussi à \(c_0 < 0\). L'unique solution positive de (26) est \[i_1^*=\Bigl [-c_1+\sqrt{c_1^2-4\, c_0}\, \Bigr ]/2\, .\] Considérons le cas particulier où \(4|c_0|/c_1^2\,\) est petit. Ce cas s'avère être satisfait numériquement dans toute la zone \(k_1 > k_1^*\) de la figure 4 sauf dans une bande étroite longeant la courbe \(c_1=0\), dont l'équation peut s'écrire \[q_1=Q_1(k_1)=\frac{a_1+b_1+(1-p_1)m_1+p_1\mu_1}{k_1-m_1}\, .\] On peut alors montrer que \begin{align*} i_1^* &\simeq \left\{\begin{array}{lll} -c_0/c_1 & ,& c_1 > 0\, ,\\ -c_1 & ,& c_1 < 0\, . \end{array}\right. \end{align*} L'approximation pour \(c_1 > 0\) revient à négliger le terme quadratique dans l'équation (26), tandis que l'approximation pour \(c_1 < 0\,\) revient à négliger le terme constant. Noter que puisque \(4|c_0|/c_1^2\) a été supposé petit, l'expression \(-c_0/c_1\) est beaucoup plus petite que \(-c_1\). Donc la prévalence de la tuberculose est élevée quand \(q_1 > Q_1(k_1)\) et beaucoup plus petite quand \(q_1 < Q_1(k_1)\). Mais comme (Breban et Blower, 2005 ; Gomes et coll., 2005) l'ont fait remarquer pour un modèle légèrement différent, le « seuil de réinfection » que l'on vient d'obtenir n'est pas bien défini mathématiquement (une situation semblable se produit par exemple quand on définit la largeur d'une « couche limite » en physique).

Remerciements

    Ce travail a été fait en partie alors que N.B. visitait SACEMA à Stellenbosch. Un résumé a été présenté à la 38e conférence de l'Union internationale contre la tuberculose et les maladies respiratoires, au Cap du 8 au 12 novembre 2007. On remercie S.M. Moghadas pour l'envoi de ses articles. R. Ouifki et C. Pretorius ont contribué à ce travail de manière égale.

Références bibliographiques