Sur la taille finale des épidémies avec de la saisonnalité

Résumé

On étudie d'abord un système SIR d'équations différentielles à coefficients périodiques qui décrit une épidémie dans un environnement saisonnier. Contrairement à un environnement constant, la taille finale de l'épidémie peut ne pas être une fonction croissante de la reproductivité \(\mathcal{R}_0\). De plus, de grandes épidémies peuvent se produire même si  \(\mathcal{R}_0 < 1\). Mais comme dans un environnement constant, la taille finale de l'épidémie converge vers 0 si \(\mathcal{R}_0 < 1\) et si la fraction initiale de personnes infectées converge vers 0. La taille finale de l'épidémie est supérieure à la fraction \(1-1/\mathcal{R}_0\) de la population initiale non immunisée si \(\mathcal{R}_0 > 1\,\). En résumé, la reproductivité garde la propriété classique de seuil mais de nombreuses autres propriétés ne sont plus vraies dans un environnement saisonnier. On devrait conserver ces résultats théoriques à l'esprit lorsqu'on analyse des données pour des maladies émergentes à vecteurs (virus du Nil occidental, dengue, chikungunya) ou transmises par voie aérienne (SRAS, grippe pandémique). Toutes ces maladies sont influencées par la saisonnalité.

1.   Introduction

    Considérons le système SIR suivant, qui décrit une épidémie: \begin{equation}\tag{1} \frac{dS}{dt}=-\beta(t)\, S\, I\ ,\quad \frac{dI}{dt}=\beta(t)\, S\, I - \gamma(t)\, I\ ,\quad \frac{dR}{dt}=\gamma(t)\, I\, . \end{equation} Le taux de contact \(\beta(t)\) et le taux de guérison \(\gamma(t)\) sont des fonctions continues, positives et périodiques de période τ. Ici

• \(S(t)\) est la fraction de la population qui est saine
• \(I(t)\) est la fraction qui est infectée
• \(R(t)\) est la fraction qui a guéri de l'infection et qui est immunisée.

    Si les coefficients \(\beta(t)\) et \(\gamma(t)\) sont constants, le système (1) est le système simplifié de Kermack et McKendrick (1927) (Thieme, 2003). Dans ce cas, il y a une formule implicite pour \(R^*\)  \begin{equation}\tag{3} (1-R^*)\, \exp \Bigl [\mathcal{R}_0\, \frac{R^*-r}{1-r}\Bigr ]=1-i-r. \end{equation}  \(\mathcal{R}_0=\beta/\gamma\) est la reproductivité. Il en résulte que \(R^*\) est une fonction croissante de  \(\mathcal{R}_0\), indépendante de \(t_0\,\), et une fonction croissante de \(i\). Toutes ces propriétés sont quelque peu intuitives. On a \(R^*\to r\)  si \(\mathcal{R}_0 < 1\) et \(i\to 0\,\). On a \[R^*-r\geq (1-r)(1-1/\mathcal{R}_0)\] si \(\mathcal{R}_0 > 1\), comme on le vérifie facilement en étudiant le côté gauche de (3). Voir aussi (Thieme, 2003, théorème 18.6). \(R^*\) converge si \(i\to 0\) vers une limite positive si \(\mathcal{R}_0 > 1\). Dans le cas d'une maladie émergente où r=0, cette limite peut être identifiée avec la séroprévalence après la fin de l'épidémie. Alors (3) donne une estimation de \(\mathcal{R}_0\,\). Ceci donne une estimation de la couverture vaccinale nécessaire pour prévenir une épidémie de la même maladie dans d'autres régions avec des caractéristiques similaires. (Bacaër et Guernaoui, 2006 ; Bacaër, 2007 ; Bacaer et Ouifki, 2007 ; Wang et Zhao, 2008 ; Bacaër, 2009) ont étudié le problème de la définition de la reproductivité pour les systèmes périodiques. En résumé, on a pour le système (1) \[\mathcal{R}_0=\frac{\bar{\beta}(1-r)}{\bar{\gamma}}\ , \quad \bar{\beta}=\frac{1}{\tau} \int_0^\tau \!\!\! \beta(t)\, dt\ , \quad \bar{\gamma}=\frac{1}{\tau} \int_0^\tau \!\!\! \gamma(t)\, dt\ . \] En effet, en linéarisant (1) près de l'équilibre sans maladie \((S=1-r,I=0,R=r)\,\), on voit que \[\frac{dI}{dt} \simeq \beta(t) (1-r) I - \gamma(t)\, I.\]  \(\mathcal{R}_0=1\) est visiblement le seuil pour cette simple équation linéaire périodique. Mais on peut aussi montrer que  \(\mathcal{R}_0\) est le rayon spectral de l'opérateur intégral de prochaine génération sur l'espace des fonctions continues périodiques \[\phi(t) \longmapsto \int_0^\infty K(t,x) \phi(t-x)\, dx.\] \(K(t,x)=\beta(t) (1-r) \exp(-\int_{t-x}^t \gamma(s)\, ds)\) est le taux de production de cas secondaires au temps \(t\) par une personne infectée au temps \(t-x\)  (Bacaër et Guernaoui, 2006, §5). Ce point de vue est proche de la définition « usuelle » de la reproductivité dans un environnement constant comme nombre moyen de cas secondaires produits par un cas initial. Mais la saisonnalité introduit un niveau de complexité semblable à celui des modèles épidémiques structurés par âge, pour lesquels la reproductivité est le rayon spectral d'un opérateur intégral (Diekmann et Heesterbeek, 2000). On voit aussi facilement que la reproductivité est l'unique nombre réel positif pour lequel le système linéaire périodique suivant a un multiplicateur de Floquet dominant égal à 1 : \[\frac{dI}{dt} = \beta(t)\, (1-r)\, I/\mathcal{R}_0 - \gamma(t)\, I.\] Voir (Bacaër, 2007, §3.4) et (Wang et Zhao, 2008). \(\mathcal{R}_0\) apparaît aussi dans l'analyse des processus de naissance et de mort périodiques (Bacaër, 2007, §5.2). Noter que l'on appelle reproductivité ce que certains auteurs l'appelleraient la reproductivité effective. Ils garderaient  \(\mathcal{R}_0\) pour le quotient  \(\bar{\beta}/\bar{\gamma}\). Dans tous les cas, la reproductivité ne dépend pas de la condition initiale.

    Dans la section 2, on commence par étudier quelles propriétés du système simplifié de Kermack et McKendrick restent vraies dans le cas périodique. Il s'avère que \(R^*\) peut ne pas être une fonction croissante de la reproductivité, que c'est une fonction périodique de l'instant initial, et qu'il peut ne pas être une fonction croissante de i. La première et la troisième de ces observations sont quelque peu contre-intuitives. La première observation implique qu'il peut être impossible d'estimer la reproductivité à partir de données de séroprévalence. Des simulations montrent aussi que de grandes épidémies peuvent se produire même lorsque \(\mathcal{R}_0 < 1\). Ceci se produit si la maladie est introduite durant une période favorable, si la fraction initiale de personnes infectées n'est pas trop petite, si la saisonnalité est suffisamment marquée, et si la période moyenne d'infection est courte par comparaison avec une saison. L'épidémie de chikungunya en 2007 en Italie était peut-être un pareil cas (ECDC, 2009). On ne doit pas conclure que la reproductivité est     > 1 simplement de l'observation d'un pic épidémique et l'on devrait faire attention à la manière dont la reproductivité est défini si la saisonnalité est importante. Des simulations montrent aussi que la taille finale de l'épidemie peut être très sensible à de petits changements de la reproductivité. Ceci explique peut-être pourquoi il est si difficile de prédire l'avenir d'une épidémie influencée par la saisonnalité. Cela a été remarqué lors de l'épidémie de chikungunya en 2005 et 2006 à La Réunion.

    On montre dans la section 3 que, comme dans le système simplifié de Kermack et McKendrick, \(\mathcal{R}_0=1\) est un seuil pour le système non linéaire périodique (1). On montre plus précisément que

• \(R^*-r\to 0\) si \(\mathcal{R}_0 < 1\) et \(i\to 0\,\).
• \(R^*-r\geq (1-r)(1-1/\mathcal{R}_0)\) si \(\mathcal{R}_0 > 1\) et \(0 < i < 1-r\).

2.   Simulations numériques

    Pour rester simple et à cause de l'intérêt actuel pour la grippe pandémique, on utilise le système (1), quoique la discussion sera aussi étendue à une maladie à vecteurs, le chikungunya. On peut vérifier que des remarques qualitatives similaires restent valables pour le système du §3.3. Considérons donc (1) avec par exemple \(\beta(t)=\bar{\beta} (1+\varepsilon \sin 2\pi t/\tau)\). \(\tau=1\)  représente la saisonnalité et ne peut être modifié. On suppose dans cette section que \(r=0\,\), comme pour une maladie émergente, et l'on étudie comment \(R^*\) dépend des autres paramètres: \(\bar{\beta}\), \(\varepsilon\), \(\gamma\), \(t_0\) et \(i\).

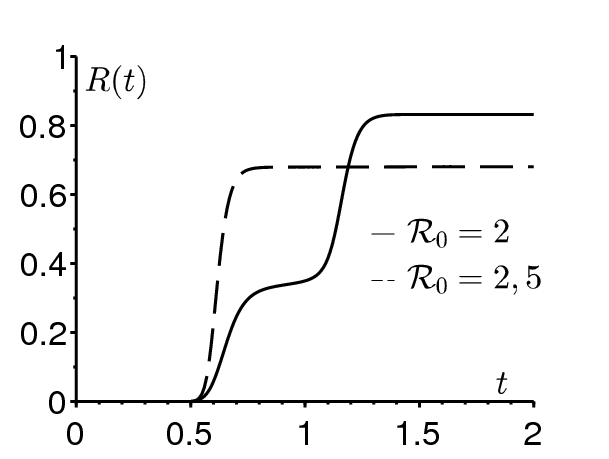
    La figure 1a montre que la taille finale de l'épidémie \(R^*\) peut ne pas croître avec la reproductivité  \(\mathcal{R}_0=\bar{\beta}/\gamma\). Les valeurs des paramètres sont  \(\varepsilon=\mbox{0,5}\), \(1/\gamma=1\) semaine \(=1/52\) année, \(t_0/\tau=\mbox{0,5}\), \(i=10^{-3}\), et l'on a pris deux valeurs pour \(\bar{\beta}\) qui correspondent à  \(\mathcal{R}_0=2\) et \(\mathcal{R}_0=\mbox{2,5}\). Avec la valeur de la reproductivité la plus grande, l'épidémie a lieu durant la saison défavorable  \(\mbox{0,5} < t/\tau < 1\), lorsque \(\beta(t)\) est inférieur à sa moyenne. Quand la saison favorable arrive (\(1 < t/\tau < \mbox{1,5}\)), la réserve de personnes saines est déjà largement réduite de sorte qu'aucune nouvelle épidémie ne se produit. Pour la valeur de la reproductivité la plus petite, la réserve de personne saines n'a pas été suffisamment entamée, une seconde vague épidémique se produit et la taille finale de l'épidémie est plus grande. Cette dernière situation est précisément ce qui s'est produit en 2005 et 2006 à La Réunion, une petite île de l'océan Indien qui est un territoire français d'outre-mer. Un premier petit pic s'est produit en mai 2005, juste avant le début de l'hiver austral. L'épidémie a traversé l'hiver à un niveau faible. Un second pic épidémique beaucoup plus grand s'est produit au début de l'été suivant en janvier 2006 et a infecté environ 250000 personnes, soit un tiers de la population de l'île. Noter enfin que si la taille finale de l'épidémie n'est pas une fonction monotone croissante de la reproductivité, alors il est impossible d'estimer la reproductivité à partir de données de séroprévalence. Cependant, on montrera dans la section 3 que \(R^*-r\geq (1-r)(1-1/\mathcal{R}_0)\). On sait donc au moins que  \(\mathcal{R}_0 \leq (1-r)/(1-R^*)\), ce qui donne une borne supérieure pour la reproductivité.

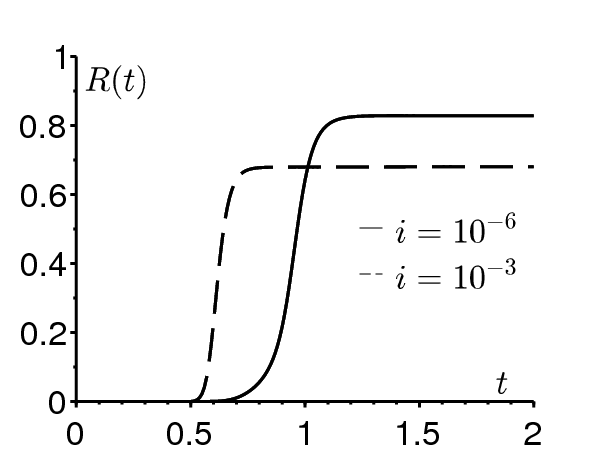
    De même, la figure 1b montre que la taille finale de l'épidémie peut ne pas croître avec la fraction initiale i de personnes infectées. Les valeurs des paramètres sont  \(\varepsilon=\mbox{0,5}\), \(1/\gamma=1/52\) année, \(t_0/\tau=\mbox{0,5}\), \(\mathcal{R}_0=\mbox{2,5}\) (ce qui détermine \(\bar{\beta}\)). On a pris \(i=10^{-6}\) et \(i=10^{-3}\). À nouveau, \(i=10^{-6}\) réduit le nombre de personnes saines plus lentement durant la saison défavorable.

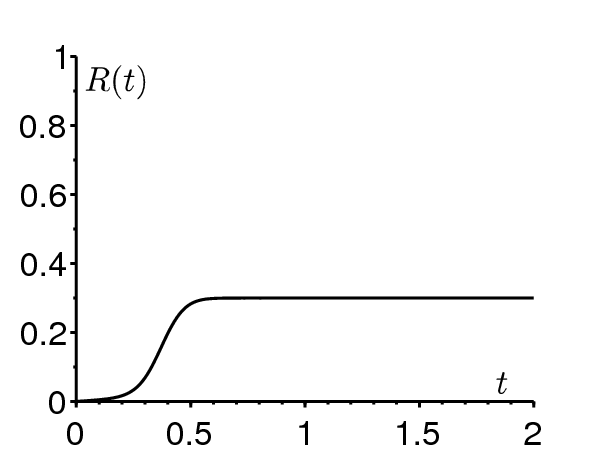
    La figure 2a montre que de grandes épidémies sont possibles même si  \(\mathcal{R}_0 < 1\). Les valeurs des paramètres sont \(\mathcal{R}_0=\mbox{0,9}\), \(\varepsilon=\mbox{0,5}\), \(1/\gamma=1/52\) année, \(t_0/\tau=0\) et \(i=10^{-3}\). Le fait que  \(\mathcal{R}_0(1+\varepsilon) > 1\) et  \(\mathcal{R}_0(1-\varepsilon) < 1\) donne une indication de ce qui arrive. Plus généralement, (1) montre que \(dI/dt < 0\) si  \(\beta(t)/\gamma(t) < 1\). L'épidémie se produit pendant la saison favorable et s'arrête simplement quand la période défavorable arrive. Le fait que la fraction initiale de personnes infectées ne soit pas trop petite (\(i=10^{-3}\)) joue aussi un rôle. En effet, le théorème du seuil avec r=0 montre que \(R^*\to 0\) si \(i\to 0\) et \(\mathcal{R}_0 < 1\). On déduit de ces remarques qu'on devrait faire attention avant d'affirmer que  \(\mathcal{R}_0 > 1\) dès qu'on observe un pic épidémique.

    Durant l'été 2007, une petite épidémie de chikungunya s'est produite près de Ravenne en Italie. L'été est la meilleure saison pour les moustiques dans cette région et l'épidémie n'aurait probablement jamais pu traversé l'hiver. À notre avis, on devrait considérer avec prudence les estimations de la reproductivité, toutes largement supérieures à 1, presentées durant la réunion sur la modélisation du chikungunya au Centre européen de contrôle et prévention des maladies (ECDC, 2009). Le problème vient essentiellement de la définition de la reproductivité et des hypothèses du modèle. Un modèle qui suppose un environnement constant semblable aux conditions estivales ne peut expliquer pourquoi l'épidémie s'arrête à l'automne; il est sûrement inadapté lorsque l'épidémie dure deux ans comme à La Réunion.

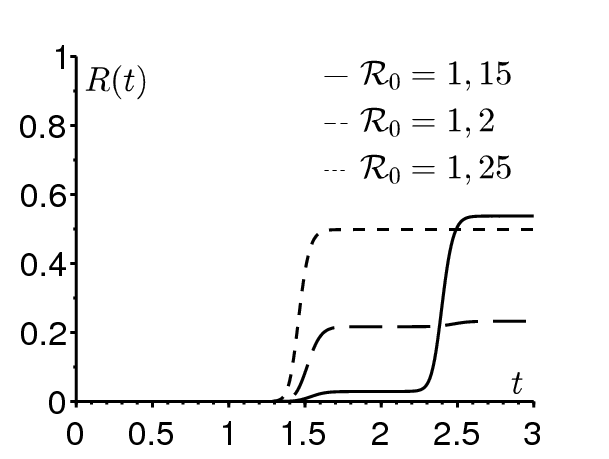
    La figure 2b montre que la taille finale de l'épidémie peut être très sensible à de petites variations de la reproductivité. Les valeurs des paramètres sont  \(\varepsilon=\mbox{0,5}\), \(1/\gamma=1/52\) année, \(t_0/\tau=\mbox{0,5}\), \(i=10^{-6}\,\), tandis que la reproductivité prend l'une des trois valeurs: 1,15 (ligne continue), 1,2 (tireté) et 1,25 (ligne en pointillé). On obtient \(R^*\simeq 54\%\) si  \(\mathcal{R}_0=\mbox{1,15}\), \(R^*\simeq 23\%\) si \(\mathcal{R}_0=\mbox{1,2}\) et \(R^*\simeq 50\%\) si \(\mathcal{R}_0=\mbox{1,25}\). En pratique, il n'est pas possible de distinguer des valeurs de la reproductivité aussi proches. Or la taille finale de l'épidémie correspondante varie d'un facteur 2. Dans les systèmes à coefficients périodiques comme (1), la prévision de la taille finale de l'épidémie semble très difficile. C'est peut-être une réponse aux critiques dirigées contre les épidémiologistes qui ont suivi l'épidémie de chikungunya à La Réunion. Bien qu'un réseau de surveillance ait soigneusement suivi l'épidémie depuis ses débuts en avril 2005, les épidémiologistes n'ont pas été capables de prévoir le grand pic qui s'est produit en janvier et février 2006. La population a ainsi mis sous pression l'Institut de veille sanitaire, chargé du suivi des maladies en France et dans ses territoires d'outre-mer. Nos simulations suggèrent que cette pression était peut-être injustifiée. D'une certaine manière, les prévisions épidémiques au-delà de quelques semaines dans un environnement saisonnier sont peut-être aussi incertaines que les prévisions météorologiques au-delà de quelques jours. L'analyse des maladies endémiques dans un environnement saisonnier, en lien avec le chaos, est une difficulté différente de celle étudiée ici.

    Pour la figure 2b, on a choisi \(i=10^{-6}\). En pratique, il est difficile d'estimer la fraction initiale i de personnes infectées. Le problème est que le système SIR suppose des contacts homogènes. Si une épidémie démarre dans une ville à partir d'un seul cas initial, on peut penser que la fraction i est simplement égale à l'inverse de la population de la ville. Mais si la ville est grande, alors il n'est peut-être pas raisonnable de supposer les contacts homogènes et l'on peut penser utiliser la population du quartier de la ville où le cas initial a été introduit. Le problème est le même pour les épidémies dans une petite île comme La Réunion mais avec environ 800000 habitants concentrés le long de la côte.

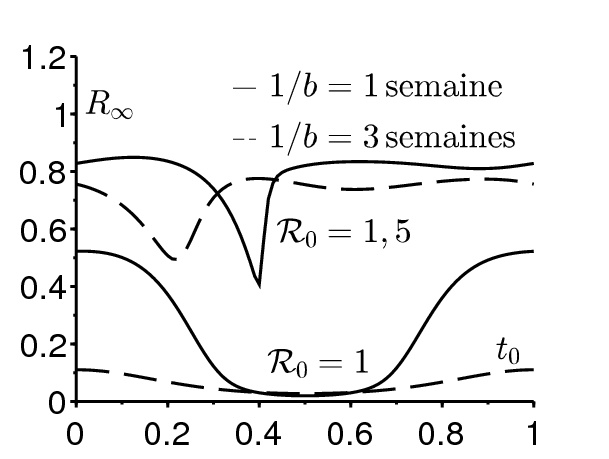
    La figure 3a étudie la dépendance de la taille finale de l'épidémie par rapport à l'instant auquel l'épidémie commence. Bien sûr, la taille finale est toujours une fonction périodique de \(t_0\) puisque le système (1) est invariant par un décalage de τ en temps. Les valeurs des paramètres dans la figure 3a sont \(\mathcal{R}_0\in \{1\, ; \, 1,5\}\), \(\varepsilon=\mbox{0,5}\), \(1/\gamma=1\) semaine ou 3 semaines et \(i=10^{-3}\). La dépendance par rapport à \(t_0\) est importante si la reproductivité est proche de 1 et si la période infectieuse est courte par rapport à la période τ. Dans un cas pareil, l'épidémie ne peut se développer durant la saison défavorable.

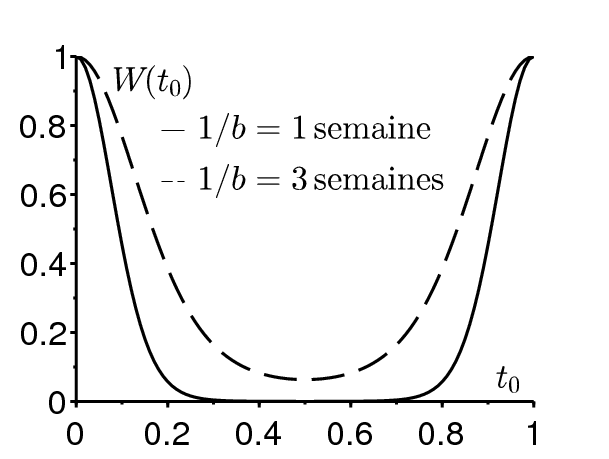
    La figure 3b montre pour \(\mathcal{R}_0=1\) la « valeur reproductive » \(V(t_0)\) ( « valeur infectieuse » serait une expression plus appropriée ) d'un cas initial introduit au temps \(t_0\), calculée avec l'équation linéarisée près de l'équilibre sans maladie: \begin{equation}\tag{4} \frac{dI}{dt} = \beta(t)\, (1-r)\, I(t) -\gamma(t)\, I(t)\, . \end{equation} On considère ici le cas général, pas seulement le cas particulier avec \(r=0\) et  \(\gamma(t)\) constant. Rappelons que le taux de croissance asymptotique de (4) est  \(\rho=\bar{\beta}(1-r)-\bar{\gamma}\) et que c'est l'unique nombre réel pour lequel l'équation suivante a une solution périodique non nulle \[ \frac{dJ}{dt} + \rho\, J(t)= \beta(t)\, (1-r)\, J(t) -\gamma(t)\, J(t)\, \] comme on peut le voir avec \(I(t)=J(t) \exp(\rho t)\) dans (4). (Bacaër et Abdurahman, 2008, §2) a montré que la valeur reproductive dans les modèles de population linéaires périodiques en temps tels que (4) ne dépend pas de « l'âge » (ici, le temps écoulé depuis l'infection) et il est donné par toute solution non nulle de l'équation adjointe \[-\frac{dV}{d{t_0}} + \rho\, V(t_0)= \beta(t_0)\, (1-r)\, V(t_0) - \gamma(t_0)\, V(t_0) \, .\] Ceci donne \[V(t_0)=\exp \Bigl [ \int_0^{t_0} (\gamma(t)-\bar{\gamma})\, dt - (1-r) \int_0^{t_0} (\beta(t)-\bar{\beta})\, dt \Bigr ]\] à une constante multiplicative près. La figure 3b comparée à la figure 3a où \(\mathcal{R}_0=1\) montre que la valeur reproductive donne seulement une vague idée de la dépendance de la taille finale de l'épidémie par rapport à \(t_0\) : on s'attend juste à ce que le maximum de \(R^*\) soit atteint près de \(t_0=0\) et le minimum près de \(t_0=\mbox{0,5}\). Avec  \(\mathcal{R}_0=\mbox{1,5}\), l'allure de \(V(t_0)\) est similaire, avec un maximum en \(t_0=0\) et un minimum en \(t_0=\mbox{0,5}\) (non montré) mais la figure 3a montre que ceci est trompeur: les effets non linéaires deviennent importants. Avec une période d'infection plus longue (\(1/\gamma=3\) semaines), la différence entre une épidémie débutant à une saison défavorable et une autre débutant à une saison favorable est moins prononcée que lorsque la période d'infection est plus courte (\(1/\gamma=1\) semaine).

    Voici enfin quelques remarques au sujet d'une méthode d'estimation de la reproductivité à partir des données sans utiliser la taille finale de l'épidémie. Au tout début d'une épidémie,  \(t\simeq t_0\), \(S\simeq 1\), \(I\simeq 0\) et \(R\simeq 0\). On a donc \(dI/dt\simeq (\beta(t_0)-\gamma) I\) et \(I(t)\) tend à croître exponentiellement au taux  \(\beta(t_0)-\gamma\). On peut estimer ce taux avec le début de la courbe épidémique. Connaissant la duré moyenne de l'infection, on peut en déduire \(\beta(t_0)\) et donc le quotient  \(\beta(t_0)/\gamma\). Mais notre analyse montre que ce quotient n'est pas lié à des propriétés de seuil du système. Ce n'est donc pas un bon candidat pour être appelé « reproductivité ». Si cependant  \(\beta(t)=\bar{\beta}\, f(t)\), et si \(f(t)\) est connu et périodique de moyenne égale à 1, alors on peut calculer \(\mathcal{R}_0 = (\beta(t_0)/\gamma)/f(t_0)\). Noter que  \(\beta(t_0)/\gamma\) surestime (ou sous-estime) \(\mathcal{R}_0\) si \(f(t_0) > 1\) (ou \(f(t_0) < 1\)), c'est-à-dire si l'épidémie débute pendant une période favorable (ou défavorable) où  \(\beta(t)\) est au-dessus (ou au-dessous) de sa moyenne \(\bar{\beta}\). Pour les maladies transmises par voie aérienne, il est difficile de connaître la forme de  \(f(t)=\beta(t)/\bar{\beta}\) parce qu'il est difficile d'estimer quantitativement l'influence de la température et de l'humidité sur la transmissibilité. Pour les maladies à vecteurs, les variations saisonnières de la population de vecteurs peuvent se mesurer. On peut donc estimer la reproductivité. Voir par exemple (Bacaër et Guernaoui, 2006).

3.   Théorèmes de seuil

3.1   Le système périodique \(\text{S-I-R}\)

    Remarques préliminaires. Il résulte de (Thieme, 2003, § A.1) que (1)-(2) a une unique solution définie pour tout t et que \(S(t) > 0\) et \(I(t) > 0\ \forall t\geq t_0\). Par ailleurs, la fonction \(S(t)\) est décroissante, \(R(t)\) est croissante et \(S+I+R=1\). On a donc \(S(t)\to S^*\) et \(R(t)\to R^*\)  si \(t\to +\infty\). Parce que \(I=1-S-R\,\), on voit que \(I(t)\to I^*\). Mais \(R(t)-r=\int_{t_0}^t \gamma(u)\, I(u)\, du\). Donc cette intégrale converge si \(t\to +\infty\). On a \(\bar{\gamma} > 0\) et donc \(I^*=0\).

    Sous le seuil. Supposons  \(\mathcal{R}_0 < 1\). Avec \(S(t)=1-I(t)-R(t)\), \(I(t)\geq 0\) et \(R(t)\geq r\ \forall t\geq t_0\,\), on a \[\frac{dI}{dt}=\beta(t) (1-I-R) I - \gamma(t) I \leq [\beta(t)(1-r)-\gamma(t)] I(t).\] Avec \(I(t_0)=i\,\), on obtient \[I(t)\leq i \exp\Bigl (\int_{t_0}^t \bigl [\beta(u)(1-r)-\gamma(u)\bigr ]\, du\Bigr ).\] Mais \(dR/dt=\gamma(t) I\) et \(R(t_0)=r\). On a donc \begin{equation}\tag{5} r\leq R(t)\leq r+i \int_{t_0}^t \gamma(u) \exp\Bigl (\int_{t_0}^u \bigl [\beta(v)(1-r) - \gamma(v)\bigr ]\, dv\Bigr ) du. \end{equation} On a \[\int_{t_0}^u [\beta(v)(1-r) - \gamma(v)]\, dv \sim [\bar{\beta}(1-r)-\bar{\gamma}]\, u, \quad u\to +\infty\, .\] Mais  \(\bar{\beta}(1-r)-\bar{\gamma} < 0\) parce que  \(\mathcal{R}_0 < 1\). Donc l'intégrale du côté droit de (5) converge si \(\ t\to +\infty\) et \[r\leq R^*\leq r+i \int_{t_0}^\infty \gamma(u) \exp\Bigl (\int_{t_0}^u \bigl [\beta(v)(1-r)-\gamma(v)\bigr ]\, dv\Bigr ) du.\] On a donc \(R^*(t_0,i,r)\to r\) si \(i\to 0\).

    Au-dessus du seuil. On suppose  \(\mathcal{R}_0 > 1\). La preuve se fait par l'absurde. On suppose \(R^*-r < (1-r)(1-1/\mathcal{R}_0)\). On a alors \(1-R^* > (1-r)/\mathcal{R}_0=\bar{\gamma}/\bar{\beta}\). Parce que \(R(t)\) est une fonction croissante, on voit que \(R(t)\leq R^*\ \forall t\geq t_0\). On a alors \begin{equation}\tag{6} \frac{dI}{dt}=\beta(t) (1-I-R) I-\gamma(t) I \geq \alpha(t) I - \beta(t) I^2, \end{equation} avec \(\alpha(t)=\beta(t)(1-R^*) -\gamma(t)\). De plus, \[\bar{\alpha}=\frac{1}{\tau} \int_0^\tau \alpha(t)\, dt = \bar{\beta}(1-R^*) -\bar{\gamma} > 0.\] Choisissons \(\eta\) avec \(0 < \eta < \bar{\alpha}/\bar{\beta}\). Parce que \(I(t)\to 0\) si \(t\to +\infty\,\), on peut trouver \(t_1 > t_0\) avec \(0\leq I(t)\leq \eta\ \forall t\geq t_1\). Or l'équation (6) implique que \[\frac{dI}{dt} \geq (\alpha(t)-\beta(t)\, \eta) I\quad \forall t\geq t_1.\] On a donc \[I(t)\geq I(t_1) \exp(\int_{t_1}^t (\alpha(u)-\beta(u) \eta)\, du),\quad \forall t\geq t_1.\] À cause du choix de η, on obtient \(I(t)\to +\infty\) si \(t\to +\infty\), ce qui contredit \(I(t)\leq 1\). On a ainsi \(R^*-r\geq (1-r)(1-1/\mathcal{R}_0)\).

3.2   Un système SEIR périodique

    Le modèle et la définition de  \(\mathcal{R}_0\). Considérons le système \[ \frac{dS}{dt}=-\beta(t) S\, I,\quad \frac{dE}{dt}=\beta(t) S\, I - \delta(t) E,\quad \frac{dI}{dt}=\delta(t) E-\gamma(t) I,\quad \frac{dR}{dt}=\gamma(t) I ,\] avec \(S+E+I+R=1\) et où le taux  \(\delta(t)\) pour passer du compartiment latent au compartiment infectieux peut aussi être périodique avec \(\bar{\delta} > 0\). Considérons la condition initiale \[S(t_0)=1-e-i-r,\quad E(t_0)=e,\quad I(t_0)=i,\quad R(t_0)=r,\] avec \(e\geq 0\), \(i\geq 0\), \(r\geq 0\), \(e+i > 0\) et \(e+i+r < 1\). Si λ>0, on définit  \(\Phi(t,t_0;\lambda)\) l'opérateur d'évolution associé avec le système linéaire périodique de période τ \begin{equation}\tag{7} \frac{d}{dt}\left (\begin{array}{c} \tilde{E}\\ \tilde{I} \end{array}\right ) = \left (\begin{array}{cc} - \delta(t) & \frac{\beta(t)(1-r)}{\lambda} \\ \delta(t) & -\gamma(t) \end{array} \right ) \left (\begin{array}{c} \tilde{E}\\ \tilde{I} \end{array}\right ) . \end{equation} Le rayon spectral  \(\sigma(\lambda)\) de  \(\Phi(t_0+\tau,t_0;\lambda)\) est le multiplicateur de Floquet dominant de (7) et ne dépend pas de \(t_0\). Les coefficients hors diagonale de (7) sont positifs. (Aronsson et Kellogg, 1978, lemme 2) implique que \(\Phi(t,t_0;\lambda)\) est une matrice positive  \( \forall t > t_0\). De plus, \(\sigma(\lambda)\) est une fonction décroissante de  \(\lambda\)  (Wang et Zhao, 2008). Dans (Bacaër, 2007, §3.4) (voir aussi (Wang et Zhao, 2008), la reproductivité  \(\mathcal{R}_0\) est définie comme l'unique λ > 0 avec  \(\sigma(\lambda)=1\).

    Quelques remarques. Il résulte de (Thieme, 2003, § A.1) que

• le système SEIR périodique a une unique solution définie pour tout t
• \(S(t) > 0\), \(E(t) > 0\) et \(I(t) > 0\ \forall t > t_0\).

    Sous le seuil. Avec \(S=1-E-I-R\,\), on a \[ \frac{d}{dt}\left (\begin{array}{c} E\\ I \end{array}\right )\leq \left (\begin{array}{cc} - \delta(t) & \beta(t)(1-r)\\ \delta(t) & -\gamma(t) \end{array} \right ) \left (\begin{array}{c} E\\ I \end{array}\right )\ , \] où l'inégalité entre vecteurs signifie l'inégalité composante par composante. On a donc \((E(t),I(t))'\leq \Phi(t,t_0;1) (e,i)'\), où le signe \('\) désigne la transposition. Dans le cas  \(\mathcal{R}_0 < 1\,\), on a \(\sigma(1) < 1\) et \[\|\Phi(t,t_0;1)\| \leq K \exp(-\xi (t-t_0))\] avec \(K > 0\) et \(\xi > 0\) (Hale, 1980, théorème 7.2). On a donc \(R^*-r=\int_0^\infty \gamma(t) I(t) dt\) converge vers 0 si e et i convergent vers 0.

    Au-dessus du seuil.  \(\mathcal{R}_0 > 1\). Imaginons que l'inégalité suivante soit fausse : \(R^*-r\geq (1-r)(1-1/\mathcal{R}_0)\). On a \[1-R^* > (1-r)/\mathcal{R}_0\,\] \[\sigma( (1-r)/(1-R^*) ) > \sigma(\mathcal{R}_0)=1.\] Par continuité du rayon spectral et parce que \(R^* < 1\), \[\exists \eta \in ]0,1-R^*[,\quad \sigma(\lambda) > 1,\] avec \(\lambda=(1-r)/(1-R^*-\eta)\). On a \(S(t)\to 1-R^*\) si \(t \to +\infty\). On a donc \[\exists t_1 > t_0,\quad \forall t\geq t_1,\quad S(t)\geq 1-R^*-\eta.\] Par conséquent, \begin{equation} \frac{d}{dt}\left (\begin{array}{c} E\\ I \end{array}\right )\geq \left (\begin{array}{cc} - \delta(t) & \beta(t)(1-R^*-\eta)\\ \delta(t) & -\gamma(t) \end{array} \right ) \left (\begin{array}{c} E\\ I \end{array}\right ) \end{equation} et \((E(t),I(t))' \geq \Phi(t,t_1;\lambda)\, (E(t_1),I(t_1))'\ \forall t\geq t_1\). En particulier, \[\left (\begin{array}{c} E(t_1+n\tau)\\I(t_1+n\tau) \end{array}\right )\geq \Phi(t_1+n\tau,t_1;\lambda) \left (\begin{array}{c} E(t_1)\\I(t_1) \end{array}\right )=\Phi(t_1+\tau,t_1;\lambda)^n \left (\begin{array}{c} E(t_1)\\I(t_1) \end{array}\right )\] pour tout entier n≥1. Les valeurs propres de la matrice positive  \(\Phi(t_1+\tau,t_1;\lambda)\) sont \(\mu_1\) et  \(\mu_2\).  \(\mu_1=\sigma(\lambda)\) est la valeur propre dominante, selon le théorème de Perron et Frobenius (Berman et Plemmons, 1979). D'après la formule de Liouville \[\mathrm{det} [\Phi(t_1+\tau,t_1;\lambda)]=\mu_1 \mu_2=\exp\Bigl (-\int_0^\tau [\delta(t) + \gamma(t)] dt\Bigr )=\exp\bigl (-(\bar{\delta}+\bar{\gamma})\tau\bigr ) < 1.\] Parce que \(\mu_1=\sigma(\lambda) > 1\,\), on a \(\mu_2\in \mathbb{R}\)  et \(0 < \mu_2 < 1\). D'après le théorème de Perron et Frobenius, on peut trouver un vecteur propre positif \((p_{1,1},p_{2,1})'\)  avec \[\Phi(t_1+\tau,t_1;\lambda) \, (p_{1,1},p_{2,1})' = \mu_1 \, (p_{1,1},p_{2,1})'.\] On choisit \((p_{1,2},p_{2,2})'\in \mathbb{R}^2 \setminus 0\) avec \[\Phi(t_1+\tau,t_1;\lambda) \, (p_{1,2},p_{2,2})' = \mu_2 \, (p_{1,2},p_{2,2})'.\] Les vecteurs propres positifs ne peuvent être associés qu'à la valeur propre dominante (Berman et Plemmons, 1979, théorème 2.1.4). On a donc  \(p_{1,2}\, p_{2,2} < 0\). On peut donc supposer que \(p_{2,2} > 0\) et \(p_{1,2} < 0\). On définit \[P=\left (\begin{array}{cc} p_{1,1} & p_{1,2}\\ p_{2,1} & p_{2,2} \end{array} \right ).\] On a alors  \(\Phi(t_1+\tau,t_1;\lambda)^n= P\, \mathrm{diag}(\mu_1^n,\mu_2^n)\, P^{-1}\) pour tout entier n≥1. \(\Delta=p_{1,1} p_{2,2} - p_{1,2} p_{2,1} > 0\) est le déterminant de P. On a alors \begin{align*} & \left (\begin{array}{c} E(t_1+n\tau)\\I(t_1+n\tau) \end{array}\right ) \geq \frac{1}{\Delta} \left (\begin{array}{cc} p_{1,1} & p_{1,2}\\ p_{2,1} & p_{2,2} \end{array} \right ) \left (\begin{array}{cc} \mu_1^n & 0\\ 0 & \mu_2^n \end{array} \right ) \left (\begin{array}{cc} p_{2,2} & -p_{1,2}\\ -p_{2,1} & p_{1,1} \end{array} \right )\left (\begin{array}{c} E(t_1)\\I(t_1) \end{array}\right )\\ &\quad = \frac{1}{\Delta} \left (\begin{array}{c} \mu_1^n\, p_{1,1} \, [p_{2,2}\, E(t_1) - p_{1,2}\, I(t_1) ] + \mu_2^n\, p_{1,2} \, [-p_{2,1}\, E(t_1) + p_{1,1}\, I(t_1) ]\\ \mu_1^n\, p_{2,1} \, [p_{2,2}\, E(t_1) - p_{1,2}\, I(t_1) ] + \mu_2^n\, p_{2,2} \, [-p_{2,1}\, E(t_1) + p_{1,1}\, I(t_1) ] \end{array}\right ). \end{align*} Parce que \(\mu_1 > 1\), \(0 < \mu_2 < 1\), \(\Delta > 0\), \(p_{1,1} > 0\), \(p_{2,1} > 0\) et \(p_{2,2}\, E(t_1) - p_{1,2}\, I(t_1) > 0\,\), on a \[E(t_1+n\tau) \mathop{\longrightarrow}_{n\to +\infty} +\infty,\quad I(t_1+n\tau) \mathop{\longrightarrow}_{n\to +\infty} +\infty.\] Mais ceci contredit le fait que \((E(t),I(t))\to (0,0)\) si \(t\to +\infty\). On a donc \(R^*-r\geq (1-r)(1-1/\mathcal{R}_0)\).

3.3   Un système périodique pour une maladie à vecteurs

    Considérons le système pour une maladie à vecteurs \[\frac{dS}{dt}=- \frac{\beta S J}{H},\quad \frac{dI}{dt}= \frac{\beta S J}{H} -\gamma\, I,\quad \frac{dR}{dt}=\gamma\, I ,\quad \frac{dJ}{dt}= \beta'(V(t)-J)I- \delta\, J,\] avec

• \(V(t)\) : une population périodique de vecteurs
• \(H\)  : la population humaine totale, \(S+I+R=H\),
• \(J\) : le nombre de vecteurs infectés,
•  \(\delta\) : la mortalité des vecteurs,
•  \(\beta\) (respectivement \(\beta'\)) : le taux auquel piquent les vecteurs multiplié par la probabilité de transmission du vecteur à l'humain (respectivement de l'humain au vecteur).

• \(R^*-r \to 0\) si \(\mathcal{R}_0 < 1\), \(i\to 0\) et \(j\to 0\),
• \(R^*-r\geq (1-r)(1-1/\mathcal{R}_0)\) si \(\mathcal{R}_0 > 1\).

4.   Conclusion

    Notre analyse montre que le théorème de seuil pour les systèmes à coefficients constants (avec les deux cas classiques, \(\mathcal{R}_0 < 1\) et \(\mathcal{R}_0 > 1\)) se généralise aux systèmes avec des coefficients périodiques qui représentent la saisonnalité, pourvu que la reproductivité  \(\mathcal{R}_0\) soit définie comme dans nos travaux antérieurs (Bacaër et Guernaoui, 2006 ; Bacaër, 2007 ; Bacaer et Ouifki, 2007). Cependant, de manière quelque peu inattendue, les systèmes périodiques peuvent donner lieu à des épidémies assez grandes même lorsque  \(\mathcal{R}_0 < 1\). La taille finale de l'épidémie peut de pas croître avec  \(\mathcal{R}_0\) ou avec la fraction initiale \(i\) de personnes infectées.

    Ces observations basées sur des systèmes simples devraient servir d'avertissement pour l'interprétation des épidémies influencées par la saisonnalité. Les épidémies émergentes de maladies à vecteurs, auxquelles la théorie du changement climatique accorde une attention particulière, devraient être analysées avec précaution comme on l'a vu avec le cas du chikungunya à La Réunion et en Italie.

    Un autre cas intéressant de nos jours est celui de la grippe pandémique chez les humains, suivant celle chez les oiseaux. La pandémie de 1918-1919 s'est produite en plusieurs vagues influencées par la saisonnalité. Des tentatives d'estimation de la reproductivité pour cette pandémie ont supposé des coefficients constants et ont utilisé le début de la courbe épidémique ou la taille finale d'épidémies à une seule vague. Voir par exemple (Vynnycky et coll., 2007).

    Notre travail suggère que ces analyses doivent peut-être être révisées. La relation entre  \(\mathcal{R}_0\) et le comportement des épidémies influencées par la saisonnalité n'est pas une généralisation évidente de ce qui est connu dans le cas d'un environnement constant.

Remerciements

    Ce travail a débuté alors que N.B. visitait l'Institut Gulbenkian des sciences, avec un financement du Conseil Portugais pour la Recherche (FCT) et de la Commission européenne (MEXT-CT-2004-14338). N.B. remercie également le Centre européen de contrôle et prévention des maladies pour son invitation à une réunion sur la modélisation du chikungunya.

Références bibliographiques