Les généalogies avec saisonnalité, la reproductivité et la pandémie de grippe

Résumé

1.   Introduction

    Rappelons brièvement quelques notions concernant la reproductivité dans un environnement constant (Diekmann et Heesterbeek, 2000). Considérons une population structurée avec m « types » de personnes infectées.  \(J_i(t)\,\) est le nombre de nouvelles infections par unité de temps, au temps t, de type \(\,i\) avec \(1\leq i \leq m\). C'est l'incidence, à ne pas confondre avec le nombre de personnes infectées. On définit \(\,J(t)=(J_1(t),\ldots,J_m(t))\). De nombreux modèles épidémiques conduisent, après linéarisation près de l'état stationnaire sans maladie, à un système d'équations de renouvellement \begin{equation}\tag{1} J(t)=\int_{0}^{t-t_0} K(\tau)\, J(t-\tau)\, d\tau + H(t)\; ,\quad \forall \, t\geq t_0. \end{equation}  \(H(t)\) est une fonction vectorielle donnée par les conditions initiales.  \(K(\tau)\,\) est une matrice carrée à coefficients positifs ou nuls. La reproductivité est définie comme le rayon spectral de la matrice de prochaine génération \[R_0=\rho(\mathcal{K}),\quad \mathcal{K}=\int_0^\infty K(\tau)\, d\tau.\] Elle s'interprète de la manière suivante. On définit \[ J(t)=\sum_{n\geq 1} J^{(n)}(t),\quad J^{(1)}(t)=H(t),\quad J^{(n+1)}(t)=\int_{0}^{t-t_0}\!\! K(\tau)\, J^{(n)}(t-\tau)\, d\tau\; , \quad t\geq t_0, \quad n\geq 1. \] \(J^{(n)}(t)\,\) est le vecteur des incidences appartenant à la génération n au temps t. \(\,\|G^{(n)}\|\,\) est la taille de la génération n, avec \begin{equation}\tag{2} G^{(n)}=\int_{t_0}^\infty \!\! J^{(n)}(t)\, dt,\quad \| G^{(n)}\|=\sum_{i=1}^m |G^{(n)}_i| = \sum_{i=1}^m G^{(n)}_i\; . \end{equation} Comme (Inaba et Nishiura, 2008) l'ont remarqué, on a \[ G^{(n+1)}= \int_{t_0}^\infty \!\! \int_{0}^{t-t_0} \!\! K(\tau)\, J^{(n)}(t-\tau)\, d\tau\, dt = \int_0^\infty \!\! K(\tau) \int_{t_0+\tau}^\infty \!\! J^{(n)}(t-\tau)\, dt\, d\tau =\mathcal{K}\, G^{(n)}.\] Si la matrice \(\mathcal{K}\) est primitive, alors le théorème de Perron et Frobenius implique que  \(G^{(n)}/(R_0)^n\) converge si \(n\to +\infty\) vers un vecteur propre à composantes strictement positives de  \(\mathcal{K}\). \(R_0\) est le taux asymptotique de croissance par génération: \[\lim_{n\to +\infty} \sqrt[n]{\|G^{(n)}\|}= R_0.\]

    Dans les modèles épidémiques structurés par âge, la structure de la population n'est pas un ensemble discret mais par exemple l'intervalle  \((0,+\infty)\). La théorie est alors très semblable: \(\,R_0\) est le rayon spectral d'un opérateur intégral de prochaine génération avec un noyau \(\mathcal{K}(x,y)\) et \[G^{(n+1)}(x)=\int_0^\infty \mathcal{K}(x,y)\, G^{(n)}(y)\, dy.\] D'après le théorème de  \(\text{Krein}\) et Rutman,  \(\,G^{(n)}/(R_0)^n\) converge vers une fonction propre positive de l'opérateur intégral.  \(R_0\,\) est encore le taux asymptotique de croissance par génération.

    Enfin si la structure de la population est discrète mais avec seulement un type (\(m=1\)), on a  \(G^{(n+1)}= R_0\, G^{(n)}\). Dans ce cas particulier, la reproductivité n'est pas simplement le taux asymptotique de croissance par génération. C'est aussi le nombre moyen de cas secondaires infectés par un premier cas.

    Dans de nombreuses applications, il est plus réaliste de supposer que l'environnement est périodique, par exemple à cause de la saisonnalité. C'est le cas pour la plupart des maladies à vecteurs, des maladies transmises par l'eau et certaines maladies transmises par voie aérienne telle que la grippe. De nombreux modèles épidémiques périodiques conduisent, après linéarisation près de l'état sans maladie, à un système d'équations intégrales de la forme (1) mais avec un noyau matriciel qui dépend aussi du temps t, de manière périodique, avec une période T. Par le passé, Heesterbeek et Roberts (1995) ont avancé que :

« the concept of \(\,R_0\,\) does not make sense in a nonautonomous setting ».

« concepts such as the basic reproductive number \(\,R_0\,\) no longer apply ».

« no general method exists for calculating the basic reproduction number, the threshold for disease extinction, in nonautonomous epidemic models ».

    Plusieurs articles ont discuté de cette définition. Bacaër et Guernaoui (2006) ont estimé la reproductivité pour une épidémie de leishmaniose et obtenu une formule analytique dans un cas particulier. Bacaër (2007) a comparé plusieurs méthodes pour calculer la reproductivité numériquement, obtenu des formules approchées lorsque l'amplitude de la saisonnalité est petite, et estimé la reproductivité pour une épidémie de chikungunya. Bacaër et Ouifki (2007) ont revisité le cas où la saisonnalité est sinusoïdale, ce qui conduit à une équation caractéristique simple pour la reproductivité.

    Wang et Zhao (2008) ont étudié le cas particulier des systèmes d'équations différentielles ordinaires, généralisé la méthode de (Bacaër, 2007) utilisant la théorie de Floquet, et démontré rigoureusement quelques propriétés de la reproductivité. Bacaër et Abdurahman (2008) ont étudié des cas de résonance, où la reproductivité est très différent de la valeur obtenue en moyennant les coefficients périodiques du modèle. Thieme (2009) a étudié des systèmes généraux périodiques dans des espaces de Banach ordonnés. Bacaër et Gomes (2009) ont démontré que la reproductivité sert encore de seuil pour les modèles épidémiques non linéaires dans un environnement périodique. Bacaër (2009) a adapté la définition aux modèles périodiques en temps discret. Nakata et Kuniya (2010) ont étudié le lien entre la reproductivité et la persistance dans un modèle épidémique particulier, comme (Wang et Zhao, 2008).

    Malgré ces travaux, les spécialistes de la modélisation des épidémies n'ont pas encore largement adopté la définition (3), comme on peut le voir avec les estimations récentes de la « reproductivité » pour la pandémie de grippe H1N1 (Boëlle et coll., 2009 ; Fraser et coll., 2009 ; Munayco et coll., 2009 ; Nishiura et coll., 2009 ; Pourbohloul et coll., 2009). On a obtenu ces estimations en ajustant une exponentielle au début de la courbe épidémique. Ceci ne tient pas compte de la saisonnalité. Or la saisonnalité est sûrement un facteur important pour les épidémies de grippe (Lipsitch et Viboud, 2009).

    On montre dans cet article que, comme dans le cas des populations structurées dans un environnement constant, la reproductivité définie par (3) s'interprète dans un environnement périodique comme un taux asymptotique de croissance par génération. Plus précisément, on démontre dans la section 2 que la génération n a une taille \(\,\|G^{(n)}\|\,\) avec \begin{equation}\tag{4} \limsup_{n \to +\infty} \sqrt[n]{\|G^{(n)}\|} = R_0\; . \end{equation} La petite astuce qui a conduit à la formule de récurrence \(G^{(n+1)}=\mathcal{K}\, G^{(n)}\,\) dans un environnement constant ne marche malheureusement pas dans un environnement périodique. Donc la preuve de (4) repose sur des résultats concernant le comportement asymptotique des équations de renouvellement périodiques obtenus par exemple par (Jagers et Nerman, 1985 ; Michel et coll., 2005 ; Thieme, 1984). On peut se demander si la limite supérieure dans (4) peut toujours être remplacée par une limite simple. La section 3 considère un modèle épidémique particulier avec un seul type de personne infectée, où le taux de contact, la probabilité de transmission et la vitesse de guérison dépendent du temps mais pas de la durée écoulée depuis l'infection: une démonstration différente montre que la limite supérieure peut bien être remplacée par une limite simple. La section 4 considère le cas des modèles avec un temps discret. La section 5 insiste sur le problème d'estimation de la reproductivité pour la pandémie actuelle de grippe H1N1. La reproductivité peut ne pas bien prédire la taille finale d'une épidémie. Deux appendices regroupent quelques preuves.

2.   Le taux asymptotique de croissance par génération

    Considérons une population avec m types différents de personnes infectées.  \(\,P_i(t,\tau)\,\) est le nombre de personnes de type i, au temps t, qui sont infectées depuis τ unités de temps.  \(P=(P_1,\ldots,P_m)\) est solution de l'équation aux dérivées partielles \begin{equation}\tag{5} \frac{\partial P}{\partial t}(t,\tau)+\frac{\partial P}{\partial \tau}(t,\tau) + B(t,\tau)\, P(t,\tau)=0,\quad \tau > 0,\ t > t_0, \end{equation} avec la condition initiale  \(P(t_0,\tau)\) et avec la condition au bord \begin{equation}\tag{6} P(t,0)= \int_0^\infty \!\! A(t,\tau)\, P(t,\tau)\, d\tau,\quad t > t_0. \end{equation} On suppose

• les matrices carrées \(A(t,\tau)\) et \(B(t,\tau)\,\) sont des fonctions continues, périodiques de période T par rapport à t
• pour tout  \(1\leq i,j\leq m\), \begin{equation}\tag{7} A_{i,j}(t,\tau)\geq 0,\quad B_{i,i}(t,\tau)\geq 0, \quad B_{i,j}(t,\tau)\leq 0\ \forall \ i\neq j,\quad \sum_i B_{i,j}(t,\tau)\geq 0. \end{equation}

    Lemme 1. Considérons l'opérateur linéaire borné \[L_s:V(t)\mapsto \int_0^\infty e^{-s\tau} K(t,\tau)\, V(t-\tau)\, d\tau, \quad s > -\beta,\quad V \in \mathcal{P}.\] Le rayon spectral de cet opérateur linéaire est \(\,\rho(s)\). Supposons qu'il existe \(\,s_0 > -\beta\) avec \(\rho(s_0) > 1\).
Alors il existe un unique nombre \(\,r > -\beta\) avec \(\rho(r)=1\). On appelle ce nombre r le paramètre malthusien.

    Le corollaire suivant rappelle la définition de \(R_0\)  et son lien avec le paramètre malthusien \(r\) (Bacaër et Guernaoui, 2006 ; Bacaër, 2007 ; Thieme, 2009).

    Corollaire 1. On définit \(\,R_0=\rho(0)\).

•  \(r > 0\) si \(R_0 > 1\)
• \(r=0\) si \(R_0=1\)
•  \(r < 0\) si  \(R_0 < 1\).

    Lemme 2. On définit \(\,J(t)=P(t,0)\). Alors pour  \(\,t\geq t_0\), \begin{align} J(t)&=\int_0^{t-t_0} \!\!K(t,\tau)\, J(t-\tau)\, d\tau +J^{(1)}(t) = \sum_{n\geq 1} J^{(n)}(t),\tag{10}\\ J^{(1)}(t)&= \int_{t-t_0}^\infty A(t,\tau)\, \Pi(t,t_0,\tau+t_0-t)\, P(t_0,\tau+t_0-t)\, d\tau\; ,\tag{11}\\ J^{(n+1)}(t)&=\int_0^{t-t_0} K(t,\tau)\, J^{(n)}(t-\tau)\, d\tau\; , \quad (n\geq 1), \tag{12}\\ \|J^{(n)}(t)\|&\leq (\alpha \, \gamma)^n\, e^{-\beta(t-t_0)} \frac{(t-t_0)^{n-1}}{(n-1)!}\; \int_0^\infty \|P(t_0,\tau)\|\, d\tau \; .\tag{13} \end{align}

    Preuve. L'équation de renouvellement (10) s'obtient en appliquant la méthode des lignes caractéristiques à (5)-(6). L'inégalité (13) est vraie pour \(\,n=1\) à cause de (9) et (11), et se démontre par récurrence avec (12).

    Le lemme suivant rappelle le comportement asymptotique des équations de renouvellement périodiques, étudié par (Coale, 1970 et 1972) et (Williams et Dye, 1997), démontré par (Jagers et Nerman, 1985 ; Michel et coll., 2005) si m=1, et par (Thieme, 1984, p. 261) si m≥ 1. Thieme (1984) suppose que le noyau donné par (8) est à support compact par rapport à τ : \(\,K(t,\tau)=0\,\) pour τ assez grand. Comme cette dernière condition est un peu trop restrictive d'un point de vue mathématique (mais pas d'un point de vue biologique), l'appendice 2 esquisse une adaptation de la preuve donnée par (Michel et coll., 2005) au cas où m≥ 1.

    Lemme 3. Supposons que la valeur reproductive totale à  \(t=t_0\) soit positive, c'est-à-dire \(c > 0\) dans le lemme 6 de l'appendice 2. Alors il existe une fonction périodique strictement positive \(w(t)\) avec \[\|J(t)\|\mathop{\sim}_{t\to +\infty} e^{rt}\, w(t).\]

    On arrive au théorème principal.

    Théorème 1. On définit \(\,G^{(n)}\) et  \(\|G^{(n)}\|\) comme dans (2). Alors (4) est vrai.

    Preuve. On définit \[Z^{(R)}(t)=\sum_{n\geq 1} \frac{J^{(n)}(t)}{R^n},\, \quad t\geq t_0, \quad R > 0.\] L'inégalité (13) montre que c'est toujours une série convergente. L'équation (12) et le théorème de convergence monotone pour l'échange d'une somme et d'une intégrale montrent que \[Z^{(R)}(t)-\frac{J^{(1)}(t)}{R} = \sum_{n\geq 1} \frac{J^{(n+1)}(t)}{R^{n+1}}= \int_0^{t-t_0} \!\! \frac{K(t,\tau)}{R}\, Z^{(R)}(t-\tau)\, d\tau\; .\]  \(Z^{(R)}(t)\) est donc solution de l'équation de renouvellement périodique \begin{equation}\tag{14} Z^{(R)}(t)= \int_0^{t-t_0} \frac{K(t,\tau)}{R}\, Z^{(R)}(t-\tau)\, d\tau + \frac{J^{(1)}(t)}{R}\; . \end{equation}  \(Z^{(R)}(t)\) est l'incidence dans une population où la matrice \(A(t,\tau)\) a été divisée par  \(R\). La reproductivité associée au noyau  \(K(t,\tau)/R\) est évidemment  \(R_0/R\).

    Supposons d'abord que \(R > R_0\). On a alors \(\,R_0/R < 1\). D'après le corollaire 1, le paramètre malthusien \(\,r^{(R)}\,\) associé avec (14) est strictement négatif. D'après le lemme 3, il existe une fonction périodique strictement positive  \(w^{(R)}(t)\) avec  \(\|Z^{(R)}(t)\|\sim w^{(R)}(t) \exp(r^{(R)} t)\) si \(t\to+\infty\).  \(R > R_0\) implique que \[\sum_{n\geq 1} \|G^{(n)}\|/R^n= \sum_{n\geq 1} \sum_{i=1}^m \int_{t_0}^\infty \!\!\! J^{(n)}_i(t)\, dt / R^n=\int_{t_0}^{\infty} \!\!\! \|Z^{(R)}(t)\|\, dt < +\infty\; .\] Supposons maintenant que \(R=R_0\). D'après le corollaire 1, le paramètre malthusien associé à (14) est nul. D'après le lemme 3, \(\|Z^{(R_0)}(t)\|\sim w^{(R_0)}(t)\) si \(t\to +\infty\), et \(w^{(R_0)}(t)\,\) est strictement positive et périodique. On a donc \[\sum_{n\geq 1} \|G^{(n)}\|/(R_0)^n=\int_{t_0}^{\infty} \!\!\! \|Z^{(R_0)}(t)\|\, dt=+\infty\; .\] En résumé,  \(\,1/R_0\) est le rayon de convergence de la série  \(\sum \|G^{(n)}\|\, z^n\). Le théorème 1 résulte alors du théorème de Cauchy et Hadamard pour ces séries.

    Remarques.

• Un élément \(V\in \mathcal{P}\) peut être vu comme un élément de l'espace dual \(\mathcal{P}^*\). Le produit de dualité est \[\langle V,W\rangle = \sum_i \int_0^T V_i(t)\, W_i(t)\, dt.\] Alors \[(L^*_sV)(t)=\int_0^\infty e^{-s\tau} K'(t+\tau,\tau)\, V(t+\tau)\, d\tau.\]  \(K'(t,\tau)\) est la matrice qui est la transposée de \(K(t,\tau)\). (Jagers et Nerman, 1985) utilisent \(\,L_s^*\) pour définir le paramètre malthusien.
• L'hypothèse \(\rho(s_0) > 1\,\)  dans le lemme 1 exclut les cas où trop de composantes du noyau matriciel seraient nulles. S'il existe  \(s_0 > -\beta\) tel qu'au moins une des deux conditions suivantes soient satisfaites \begin{align} & \min_{0\leq t \leq T} \min_{1\leq i\leq m} \sum_{j=1}^m \int_0^\infty e^{-s_0 \tau} K_{i,j}(t,\tau)\, d\tau > 1 ,\tag{15}\\ & \min_{0\leq t \leq T} \min_{1\leq j\leq m} \sum_{i=1}^m \int_0^\infty e^{-s_0 \tau} K_{i,j}(t+\tau,\tau)\, d\tau > 1 ,\tag{16} \end{align} on a alors \(\rho(s_0) > 1\). On définit
  •  \(\,\mathbf{1}\in \mathcal{P}\,\)  fonction dont toutes les composantes sont identiquement égales à 1
  •  \(c_1\) et \(c_2\,\) les côtés gauches de (15) et (16).
  On a alors  \(\,L_{s_0}\mathbf{1}\geq c_1\, \mathbf{1}\) ou \(L_{s_0}^*\mathbf{1}\geq c_2\, \mathbf{1}\). Par conséquent, \(\,\rho(s_0)\geq c_1 > 1\) ou \(\rho(s_0)\geq c_2 > 1\,\) (Drnovsek, 2000). L'hypothèse (15) est une généralisation de l'hypothèse (5.2) de (Michel et coll., 2005), qui correspond à  \(s_0=0\) et  \(m=1\). Rappelons que même dans la théorie de Lotka pour les populations avec un type dans un environnement constant (Feller, 1941 ; Lotka, 1939), une condition est nécessaire pour s'assurer que le côté gauche de l'équation d'Euler-Lotka prenne une valeur supérieure à 1 pour un certain s \[\int_0^\infty e^{-s\tau} K(\tau)\, d\tau=1.\]
• Rappelons la formule du rayon spectral \[R_0=\lim_{n\to \infty} \|(L_0)^n\|^{1/n}.\] Avec \[J^{(n)}(t)=0,\quad \forall t < t_0,\] (12) devient \[J^{(n+1)}(t)=\int_0^\infty \!\! K(t,\tau)\, J^{(n)}(t-\tau)\, d\tau\; .\] Avec l'hypothèse (9), on peut considérer le côté droit de cette équation comme un opérateur linéaire \(\widetilde{L}_0\) sur l'espace des fonctions \(L^1(\mathbb{R},\mathbb{R}^m)\)  à valeurs vectorielles intégrables, avec \[\|J^{(n)}\|_1=\int_{-\infty}^{+\infty}\!\! \|J^{(n)}(t)\|\, dt = \|G^{(n)}\|.\] On a alors \[J^{(n+1)}=\widetilde{L}_0\, J^{(n)}=(\widetilde{L}_0)^n\, J^{(1)}.\]  \(\|\cdot\|_1\) est la norme dans l'espace des opérateurs linéaires bornés dans  \(L^1(\mathbb{R},\mathbb{R}^m)\). Donc \[\|G^{(n+1)}\|=\|J^{(n+1)}\|_1\leq \|(\widetilde{L}_0)^n\|_1\, \|J^{(1)}\|_1.\] Le rayon spectral de \(\widetilde{L}_0\) est donné par \[\sigma(\widetilde{L}_0)=\lim \|(\widetilde{L}_0)^n\|_1^{1/n}.\] On a alors \[\limsup \sqrt[n]{\|G^{(n)}\|} \leq \sigma(\widetilde{L}_0).\] Même si l'on pouvait montrer \(\,\sigma(\widetilde{L}_0)=R_0\,\), on aurait seulement la « moitié » du théorème 1. Ce n'est pas évident : les fonctions périodiques ne sont pas dans  \(L^1(\mathbb{R},\mathbb{R}^m)\,\).

3.   Un cas particulier

    Dans cette section, on considère un cas particulier où la limite supérieure dans (4) peut être remplacée par une limite simple. On suppose

• m=1
•  \(A(t,\tau)=A(t)\) et \(B(t,\tau)=B(t)\)
• la condition initiale est une personne nouvellement infectée: \(P(t_0,\tau)=\delta_{\tau=0}\) (masse de Dirac).

    Lemme 4. Pour  \(\,n\geq 1\) et \(t > t_0\), \begin{equation}\tag{19} J^{(n)}(t)= \frac{A(t)}{(n-1)!} \Bigl [ \int_{t_0}^t \! A(s)\, ds\Bigr ]^{n-1} \exp\Bigl (-\int_{t_0}^t \! B(s)\, ds \Bigr )\; . \end{equation}

    Preuve. On procède par récurrence sur n. Pour n=1, la formule résulte de (11) et de l'hypothèse sur la condition initiale \(P(t_0,\tau)\). Supposons que la formule soit vraie pour n. On a avec (12), (17) et (19) \begin{align*} J^{(n+1)}(t)&= \frac{A(t)}{(n-1)!} \Bigl [\int_0^{t-t_0} \!\! A(t-\tau) \Bigl [ \int_{t_0}^{t-\tau} \!\! A(s)\, ds\Bigr ]^{n-1} d\tau\Bigr ] \exp\Bigl (-\int_{t_0}^t \!\! B(s)\, ds\Bigr )\\ &= \frac{A(t)}{n!} \Bigl [ \int_{t_0}^{t} A(s)\, ds\Bigr ]^{n} \exp\Bigl (-\int_{t_0}^t \!\! B(s)\, ds\Bigr )\; . \end{align*}

    Remarque. Bien sûr, on a pour l'incidence totale \[J(t)=\sum_{n=1}^\infty J^{(n)}(t) = A(t)\, \exp \Bigl [ \int_{t_0}^t A(s)\, ds - \int_{t_0}^t B(s)\, ds \Bigr ]\; .\] D'après (Bacaër et Guernaoui, 2006), le modèle de cette section vient de l'équation pour le nombre total de personnes infectées \[\frac{dI}{dt} = A(t)\, I(t) - B(t)\, I(t).\] Avec \(I(t_0)=1\), la solution est \[I(t)=\exp \left [ \int_{t_0}^t A(s)\, ds - \int_{t_0}^t B(s)\, ds \right ].\] L'incidence totale est \(J(t)=A(t)\, I(t)\).

    La propriété suivante donne une estimation de la taille de la génération n.

    Proposition 1. Pour  \(\,n\geq 1\), on a \[(R_0)^n\, \frac{e^{-\bar{B}T} (1-e^{-\bar{B}T}) }{\bar{B}T } \leq G^{(n)} \leq (R_0)^n\, \frac{e^{\bar{B}T} (e^{\bar{B}T}-1) }{\bar{B}T }\; .\] On a donc \[\lim_{n\to \infty} \sqrt[n]{G^{(n)}}= R_0.\]

    Preuve. Tout d'abord, une intégration par parties donne \[G^{(n)}=\int_{t_0}^\infty B(t)\, \exp\Bigl (-\int_{t_0}^t B(s)\, ds \Bigr ) \Bigl [ \int_{t_0}^t A(s)\, ds\Bigr ]^{n} \, \frac{dt}{n!}\; .\] La méthode de Laplace pour l'estimation asymptotique d'intégrales ne semble pas être applicable directement ici. Cependant on peut écrire \[G^{(n)}=\sum_{k=0}^{+\infty} H_k\] avec \begin{align*} H_k&=\int_{t_0+kT}^{t_0+(k+1)T} \!\!\!B(t)\, \exp \Bigl (-\int_{t_0}^t B(s)\, ds\Bigr )\, \Bigl [\int_{t_0}^t A(s)\, ds\Bigr ]^{n} \, \frac{dt}{n!} \\ &=\int_{0}^{T}\!\!\! B(t_0+\theta)\, \exp\Bigl (-\int_{t_0}^{t_0+kT+\theta}\!\!\! B(s)\, ds\Bigr )\, \Bigl [\int_{t_0}^{t_0+kT+\theta}\!\!\! A(s)\, ds\Bigr ]^{n} \, \frac{d\theta}{n!}\\ &=e^{-k \bar{B} T} \int_{0}^{T}\!\!\! B(t_0+\theta)\, \exp\Bigl ( -\int_{t_0}^{t_0+\theta}\!\!\! B(s)\, ds\Bigr )\, \Bigl [k \bar{A} T + \int_{t_0}^{t_0+\theta}\!\!\! A(s)\, ds\Bigr ]^{n} \, \frac{d\theta}{n!}. \end{align*} Par conséquent, \[e^{-k \bar{B} T}\, F_k\leq H_k \leq e^{-k \bar{B} T}\, F_{k+1}\] avec \begin{align*} F_k&=\int_{0}^{T}\!\!\! B(t_0+\theta)\, \exp\Bigl ( -\int_{t_0}^{t_0+\theta}\!\!\! B(s)\, ds\Bigr )\, \bigl [k \bar{A} T\bigr ]^{n} \, \frac{d\theta}{n!}=\frac{(k \bar{A} T)^n}{n!} (1-e^{-\bar{B}T})\; . \end{align*} Avec \(F_0=0\), on obtient \[\sum_{k=1}^{+\infty} e^{-k \bar{B} T}\, F_k\leq G^{(n)}\leq e^{\bar{B} T} \sum_{k=1}^{+\infty} e^{-k \bar{B} T}\, F_{k}.\] Mais \[e^{-\bar{B} T} \int_{k-1}^{k}\!\! e^{- \theta \bar{B} T}\, \theta^n\, d\theta \leq e^{- k \bar{B} T}\, k^n\leq e^{\bar{B} T} \int_k^{k+1} \!\! e^{- \theta \bar{B} T}\, \theta^n\, d\theta\; . \] Avec \(\int_{0}^{\infty}e^{- \theta \bar{B} T}\, \theta^n\, d\theta = n!/(\bar{B} T)^{n+1}\), on obtient \[ e^{-\bar{B} T}\, \frac{n!}{(\bar{B} T)^{n+1}} \leq \sum_{k=1}^{+\infty} e^{- k \bar{B} T}\, k^n\leq e^{\bar{B} T}\, \frac{n!}{(\bar{B} T)^{n+1}}\; . \] La proposition 1 résulte de ces estimations.

    Remarque. Le cas particulier de cette section a une autre propriété intéressante, qui résulte immédiatement de (18) et (19): pour tout  \(t > t_0\), \begin{equation} Z^{(R)}(t)=\sum_{n\geq 1} \frac{J^{(n)}(t)}{R^n}=\frac{A(t)}{R} \, \exp \Bigl [ \int_{t_0}^t \frac{A(s)}{R}\, ds - \int_{t_0}^t B(s)\, ds \Bigr ]\; . \end{equation}  \(Z^{(R_0)}(t)\) est une des fonctions propres \(U(t)\) de (3), comme dans (18).

4.   Modèles périodiques en temps discret

    On peut évidemment adapter les résultats et les preuves de la section 2 au cas des modèles périodiques de population en temps discret (Bacaër, 2009).  \(P(t)\,\) est un vecteur de taille ω, dont les composantes représentent différents temps écoulés depuis l'infection ou différents types. On suppose

•  \(P(t+1)=M(t)P(t)\), \(\forall t\geq t_0,\)
•  \(M(t)=A(t)+B(t)\)
•  \(A(t+T)=A(t)\) et \(B(t+T)=B(t)\)
•  \(A_{i,j}(t)\geq 0\), \(B_{i,j}(t)\geq 0\)
•  \(\sum_i B_{i,j}(t)\leq 1\) 
• le rayon spectral de la matrice \(B(T-1)B(T-2)\ldots B(0)\) est strictement inférieur à 1.

• la matrice \(M^*(t_0)=M(t_0+T-1) M(t_0+T-2)\cdots M(t_0)\) est primitive
• \begin{equation}\tag{20} \left (\begin{array}{ccccc} 0 & 0 &\cdots & 0 & M(T-1) \\ M(0) & 0 &\cdots &0 & 0\\ 0 & M(1) &\ddots &0 & 0\\ \vdots &\ddots & \ddots & \ddots & \vdots\\ 0 & 0 &\cdots & M(T-2) & 0 \end{array}\right) \end{equation} est irréductible.

5.   \(R_0\) et la pandémie de grippe H1N1

    L'un des modèles les plus simples tenant compte de la saisonnalité pour la pandémie de grippe H1N1 est le modèle SIR \begin{equation}\tag{21} \frac{dS}{dt}=-a(t)\, S(t)\, I(t),\quad \frac{dI}{dt}=a(t)\, S(t)\, I(t)-b\, I(t),\quad \frac{dR}{dt}=b\, I(t) \end{equation} (Bacaër et Gomes, 2009).  \(\,a(t)\,\)  a une période \(T=1\) an.  \(\,1/b\) est la durée moyenne de l'infection.  \(S(t)\) est la fraction de personnes saines, \(I(t)\) la fraction de personnes infectées et \(R(t)\,\) la fraction de personnes qui ont guéri et qui sont donc immunisées. On a ainsi \(\,S(t)+I(t)+R(t)=1\,\) pour tout t. La mortalité est négligée dans ce modèle. On introduit quelques personnes infectées de sorte que \[S(t_0)=1-\varepsilon,\quad I(t_0)=\varepsilon,\quad R(t_0)=0.\] L'un des buts principaux de la modélisation en épidémiologie est d'essayer de prédire la taille finale de l'épidémie : \[R(\infty)=\lim_{t\to \infty} R(t).\]

    Dans un environnement constant (avec \(a(t)=a\,\) indépendant de t), Kermack et McKendrick (1927) ont trouvé une relation simple entre  \(R_0=a/b\) et  \(R(\infty)\). \(R(\infty)\) est une fonction croissante de  \(R_0\), indépendante de  \(t_0\,\), et qui varie très peu avec ε si ε est assez petit. De plus, \(\,R_0\,\) peut être estimé en ajustant une exponentielle au début de la courbe épidémique. Le taux de croissance initial est \[r=a-b.\] On connaît la durée moyenne de l'infection \(1/b\). On peut donc calculer \[R_0=1+r/b.\] À cause de ces propriétés, \(\,R_0\,\) est devenu très populaire parmi les modélisateurs d'épidémies. Bien sûr, il y a beaucoup de facteurs qui compliquent les choses (population inhomogène, interventions...), et qui sont responsables du fait qu'en pratique les modèles mathématiques ont rarement prédit correctement la taille finale d'une épidémie.

    Retournons au système (21) avec un coefficient périodique. On peut encore ajuster une exponentielle au début de la courbe épidemique. C'est la méthode utilisée par (Boëlle et coll., 2009; Fraser et coll., 2009; Munayco et coll., 2009; Nishiura et coll., 2009; Pourbohloul et coll., 2009) pour la pandémie de grippe H1N1. Cette méthode n'a de sens que parce que l'ajustement se fait avec un ou deux mois de données épidémiques et parce que la fonction saisonnière de contacts, de période un an, varie peu sur une échelle de temps aussi petite. Le taux de croissance est alors à peu près \[a(t_0)-b\] et \[a(t_0)/b\] est la prétendue « reproductivité » estimée dans les références ci-dessus. Comme ces références ne considèrent pas explicitement l'effet de la saisonnalité, certains auteurs utilisent la notation \(\,R_0\,\) pour le nombre \(a(t_0)/b\). Par exemple, (Fraser et coll., 2009) trouve un nombre entre 1,4 et 1,6. Pour le système (21), on a en réalité \[R_0=\bar{a}/b.\]  \(\bar{a}\) est la moyenne de  \(a(t)\). Si l'on linéarise le système (21) près de l'état d'équilibre sans maladie  \((S=1,I=0,R=0)\), on a \[\frac{dI}{dt} = a(t)\, I(t) - b\, I(t).\] C'est précisément le cas considéré dans la section 3 mais avec b constant.

    À ce stade, on peut se demander quels sont les avantages et les désavantages d'insister sur  \(a(t_0)/b\) plutôt que sur la reproductivité  \(R_0=\bar{a}/b\), comme cela a été fait dans les études déjà citées sur la gripppe H1N1. D'un côté \(\,a(t_0)\,\) a l'avantage de pouvoir être facilement estimé avec les données épidémiques. Par comparaison, l'estimation de la reproductivité nécessiterait la connaissance a priori de  \(a(t_0)/\bar{a}\), sur lequel on a en réalité très peu d'information. Mais d'un autre côté, la reproductivité a des propriétés mathématiques précises. D'après Bacaër et Gomes (2009), la reproductivité sert de seuil pour le système (21) et l'article présent montre que c'est un taux asymptotique de croissance par génération pour les équations linéarisées près de l'état stationnaire sans maladie.

    \(a(t_0)/b\) et \(R_0=\bar{a}/b\,\) ne semblent pas bien prédire la taille finale de l'épidémie même pour des amplitudes de saisonnalité relativement petites. Considérons par exemple le cas où \[a(t)=\bar{a}(1+e\, \cos(\omega t)), \quad \omega=2\pi/T,\]  \(T=1\) an et \(b=100\,\) par an. La durée d'infection  \(1/b\,\) est comprise entre 3 et 4 jours. On suppose \(\ R_0=\bar{a}/b=\mbox{1,5}\). C'est une valeur typique pour la pandémie de grippe H1N1 (Fraser et coll., 2009). On suppose de plus \(\ \varepsilon=I(t_0)=10^{-4}\) : on introduit un cas dans une population de 10000 personnes qui se mélangent de manière homogène. Noter que le temps t du calendrier a été fixé de sorte  \(a(t)\) atteigne son maximum lorsque \(t=0\). \(t_0\) est le temps écoulé depuis ce maximum.

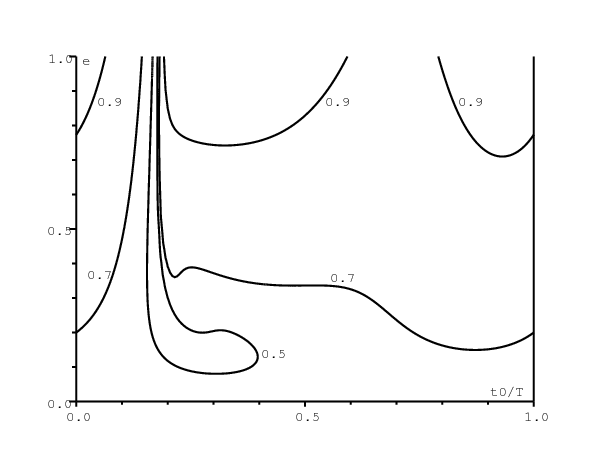
    La figure 1 montre des lignes de niveau de la taille finale de l'épidémie \(R(\infty)\in \{\mbox{0,5};\, \mbox{0,7};\, \mbox{0,9}\}\), quand on varie le temps d'introduction du premier cas infecté (\(0\leq t_0\leq T\), axe horizontal) et le niveau e de la saisonnalité (\(0\leq e\leq 1\), axe vertical). Suivant le choix de \(\,(t_0,e)\,\), la taille finale varie de 38% à 94%. Insistons sur le fait que ces différentes valeurs de \(\,R(\infty)\) correspondent à la même valeur de \(R_0\). Sur l'axe horizontal \(\,e=0\) (pas de saisonnalité), la taille finale  \(R(\infty)\) est évidemment indépendante de \(t_0\) et \(R(\infty)=58\%\). La taille finale varie selon \(\,t_0\)

• de 53% à 63% si \(\,e=5\%\,\)
• de 48% à 67% si  \(\,e=10\%\)
• de 42% à 70% si \(\,e=15\%\).

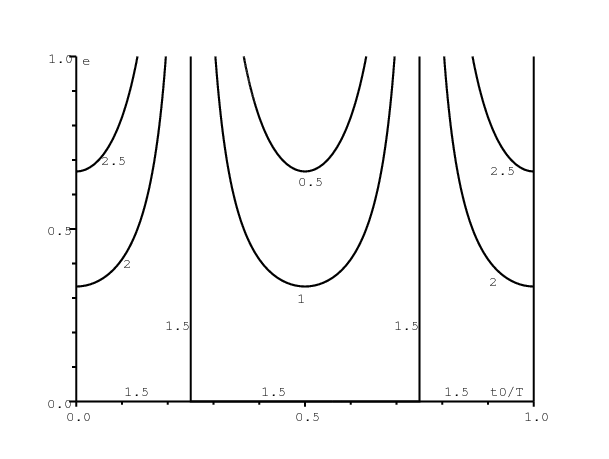
    La figure 2 montre des lignes de niveau de  \(a(t_0)/b\in \{\mbox{0,5}; 1; \mbox{1,5}; 2; \mbox{2,5}\}\,\), la prétendue « reproductivité » qui peut être estimée par ajustement d'une exponentielle au début d'une courbe épidémique. On varie le temps d'introduction du premier cas infecté (\(0\leq t_0\leq T\), axe horizontal) et l'amplitude de la saisonnalité (\(0\leq e\leq 1\), axe vertical) comme dans la figure 1. \(a(t_0)/b\,\) prédit mal la taille finale de l'épidémie. Le cas le plus frappant est celui où  \(t_0/T=\mbox{0,5}\) et \(e=1\). Dans ce cas, \(\,a(t_0)/b=0\) (voir la figure 2) mais \(R(\infty)=93\%\) (voir la figure 1)!

    Il est difficile d'estimer l'amplitude e de la saisonnalité pour des épidémies réelles. (Dushoff et coll., 2004) suggèrent que \(\,e=4\%\,\) est suffisant pour expliquer la saisonnalité de la grippe. Mais leur modèle endémique nécessite un choix très particulier des valeurs des paramètres pour obtenir un phénomène de résonance. (Cauchemez et coll., 2008) estiment que les vacances d'hiver réduisent la transmission aux enfants d'environ 25%, ce qui suggère que \(\,a(t)\,\) peut subir de grandes variations. Shaman et Kohn (2009) ont trouvé récemment une forte correlation entre la pression de vapeur et la transmission de la grippe chez les cochons d'Inde. En Suède, la pression de vapeur à l'extérieur varie de 5 millibars en hiver à 15 millibars en été. La transmission décroît alors de 80% à 20% (Shaman et Kohn, 2009, figure 1). On s'attend donc à ce que des valeurs assez grandes de l'amplitude saisonnière e soient relativement fréquentes.

Conclusion

    Cet article montre que la reproductivité dans un environnement périodique, définie ou utilisée par (Bacaër et Guernaoui, 2006 ; Bacaër, 2007 ; Bacaër et Ouifki (2007), Bacaër et Abdurahman, 2008 ; Bacaër et Gomes, 2009 ; Bacaër, 2009 ; Nakata et Kuniya, 2010 ; Thieme, 2009 ; Wang et Zhao, 2008) a la même signification biologique que dans la théorie classique dans un environnement constant: c'est un taux asymptotique de croissance par génération.

    La section 5 compare  \(R_0\,\)  avec l'estimation de la « reproductivité » que l'on obtient par ajustement d'une exponentielle au début d'une courbe épidémique. Il s'avère que les deux nombres prédisent mal la taille finale de l'épidémie. Les estimations récentes de la « reproductivité » pour la pandémie actuelle de grippe H1N1 n'ont pas pris en compte la saisonnalité, alors que la saisonnalité est certainement importante pour une maladie transmise par voie aérienne de ce genre. Il faut donc considérer avec précaution les prédictions basées sur ces estimations et les comparaisons avec les pandémies précédentes. Le problème de la définition et de l'estimation de la reproductivité n'aurait pas de conséquence pratique si ces estimations n'avaient pas quelque influence sur les décisions de santé publique, telles que les dépenses importantes faites pour acheter en avance des stocks de vaccins.

Appendice 1

    Voici une preuve du lemme 1.

    (i) Montrons que l'opérateur linéaire \(L_s\,\) est borné. L'hypothèse (9) implique \[\|e^{-s\tau} K(t,\tau)\, V(t-\tau)\|\leq \alpha\, \gamma\, e^{-(s+\beta)\tau}\, \|V\|_\infty.\] Donc la continuité de la fonction \(\,t\mapsto (L_sV)(t)\,\) résulte du théorème de convergence dominée.  \(\mathcal{L}(\mathcal{P})\) est l'espace des opérateurs linéaires bornés. On a alors \begin{equation}\tag{22} \|L_s\|_\infty\leq \max_{0\leq t \leq T} \int_0^\infty \!\! e^{-s\tau} \|K(t,\tau)\|\, d\tau \leq \frac{\alpha\, \gamma}{s+\beta}\; . \end{equation}

    (ii) Compacité de \(L_s\). Comme (Jagers et Nerman, 1985, p. 260) et (Bacaër, 2007) l'ont déjà remarqué en utilisant la périodicité du noyau, un calcul simple donne \[(L_sV)(t)=\int_0^T \widehat{K}_s(t,\theta)\, V(\theta)\, d\theta,\quad 0\leq t\leq T,\] avec \[\widehat{K}_s(t,\theta)=\sum_{n=0}^\infty K_s(t,t-\theta+nT),\quad 0\leq \theta \leq t,\] \[\widehat{K}_s(t,\theta)=\sum_{n=1}^\infty K_s(t,t-\theta+nT), \quad t < \theta \leq T,\] \[K_s(t,\tau)=e^{-s\tau}K(t,\tau).\] On a \[\forall t,\quad \forall \theta\in [0,T], \quad 0\leq \|K_s(t,t-\theta+nT)\|\leq \alpha\, \gamma\, e^{-(\beta+s)(t-\theta+nT)}\leq \alpha\, \gamma\, e^{-(\beta+s) (n-1) T}.\]  \(\widehat{K}_s(t,\theta)\) est donc une fonction continue sur  \(\{(t,\theta)\in [0,T]\times [0,T];\ t\neq \theta\}\) et une fonction bornée sur  \([0,T]\times [0,T]\).  \(\,\widehat{K}_s(t,\theta)\,\) est donc un noyau « faiblement singulier » et l'opérateur intégral  \(L_s\) est compact (Kress, 1999, théorème 2.22).

    (iii) Monotonie de \(s\mapsto \rho(s)\). Les composantes du noyau matriciel  \(K(t,\tau)\,\) sont positives ou nulles. L'opérateur linéaire \(\,L_s\) est donc aussi positif: si \(V_i\geq 0\) pour tout \(i\), ce que l'on note \(V\geq 0\), on a alors \(L_sV\geq 0\). De plus,  \(s\leq s'\) implique que \(L_s\geq L_{s'}\).  \((\mathcal{P},\|\cdot\|_\infty)\,\)  est un espace de Banach et aussi un treillis de Banach: si \(|V_i|\leq |V_i'|\) pour tout  \(i\), on a alors  \(\|V\|_\infty \leq \|V'\|_\infty\). La monotonie du rayon spectral pour les opérateurs positifs dans les treillis de Banach montre que  \(s\mapsto \rho(s)\) est décroissante (Burlando, 1991).

    (iv) Continuité de \(s\mapsto \rho(s)\).  \(s\mapsto L_s\) de \((-\beta,+\infty)\to \mathcal{L}(\mathcal{P})\) est une fonction continue parce que \[\|L_s - L_{s'}\|_\infty \leq \max_{0\leq t \leq T} \int_0^\infty \!\!\! |e^{-s\tau}-e^{-s'\tau}|\, \|K(t,\tau)\|\, d\tau \leq \alpha \gamma \int_0^\infty \!\!\! |e^{-s\tau}-e^{-s'\tau}|\, e^{-\beta \tau}\, d\tau \] et parce que le côté droit converge vers 0 quand  \(s'\to s\). Le rayon spectral est continu sur l'espace des opérateurs linéaires compacts (Degla, 2008).  \(\,s\mapsto \rho(s)\,\) est donc une fonction continue.

    (v) Existence de \(r\). Avec l'inégalité (22), on a  \(\|L_s\|_\infty\to 0\) si \(s\to +\infty\). Avec \(\,\rho(s)\leq \|L_s\|_\infty\), on a aussi \(\rho(s)\to 0\) si \(s\to +\infty\). La continuité de \(\,s\mapsto \rho(s)\) et l'hypothèse  \(\rho(s_0) > 1\) impliquent qu'il existe \(r\geq s_0\) avec  \(\rho(r)=1\).

    (vi) Log-convexité de \(s\mapsto \rho(s)\). On pourrait utiliser le théorème 2.5 de (Kato, 1982) pour la fonction \(\,s\mapsto L_s\,\) qui est « complètement monotone » et donc « surconvexe » (Thieme, 1998, théorème 2.5). Cependant une preuve un peu différente inspirée du cas en dimension finie (Bapat et Raghavan, 1997, théorème 3.3.4) peut être intéressante. On suppose  \(\,-\beta < s_1 < s_2\) et que \(s=\lambda s_1+(1-\lambda)s_2\) avec \(0 < \lambda < 1\). On voudrait montrer \[\rho(s)\leq \rho(s_1)^\lambda \rho(s_2)^{1-\lambda}.\] Grâce à la continuité du rayon spectral sur l'espace des opérateurs linéaires compacts et en considérant l'opérateur associé au noyau modifié suivant \[K^{\varepsilon}_{i,j}(t,\tau)=K_{i,j}(t,\tau)+\varepsilon\, e^{-\beta\tau},\] il suffit de démontrer la log-convexité avec l'hypothèse supplémentaire que \(L_s\) est « fortement positif »: si \(\mathcal{C}\) est le cône fermé convexe des fonctions positives dans  \(\mathcal{P}\), on a alors  \(L_s(\mathcal{C}\setminus \{0\})\) est inclus dans l'intérieur de \(\mathcal{C}\). D'après la « version forte » du théorème de  \(\text{Krein}\) et Rutman (Drabek et Milota, 2007, théorème 5.4.33), il existe des fonctions propres strictement positives  \(V^{(1)}(t)\) et \(V^{(2)}(t)\) associées aux valeurs propres \(\rho(s_1)\) et \(\rho(s_2)\) des opérateurs linéaires \(L_{s_1}\) et \(L_{s_2}\). On définit \[W_i(t)=(V^{(1)}_i(t))^\lambda\, (V^{(2)}_i(t))^{1-\lambda}.\] D'après la version discrète de l'inégalité de Hölder avec  \(p=1/\lambda\) et \(q=1/(1-\lambda)\), \begin{align*} (L_s&W)_i(t)=\int_0^\infty \!\! \sum_j \Bigl [e^{-s_1\tau} K_{i,j}(t,\tau) V^{(1)}_j(t-\tau)\Bigr ]^\lambda \Bigl [e^{-s_2\tau} K_{i,j}(t,\tau) V^{(2)}_j(t-\tau)\Bigr ]^{1-\lambda} \!\!\! d\tau\\ &\leq \int_0^\infty \! \Bigl [\sum_j e^{-s_1\tau} K_{i,j}(t,\tau) V^{(1)}_j(t-\tau)\Bigr ]^\lambda \Bigl [ \sum_j e^{-s_2\tau} K_{i,j}(t,\tau) V^{(2)}_j(t-\tau)\Bigr ]^{1-\lambda} \!\!\! d\tau. \end{align*} D'après l'inégalité de Hölder pour les intégrales, \begin{align*} (L_sW)_i(t)&\leq \Bigl \{ \int_0^\infty \!\Bigl [\sum_j e^{-s_1\tau} K_{i,j}(t,\tau) V^{(1)}_j(t-\tau)\Bigr ] d\tau \Bigr \}^\lambda \\ &\quad \quad \Bigl \{ \int_0^\infty \Bigl [ \sum_j e^{-s_2\tau} K_{i,j}(t,\tau) V^{(2)}_j(t-\tau)\Bigr ] d\tau \Bigr \}^{1-\lambda}\\ &= \bigl [\rho(s_1) V^{(1)}_i(t) \bigr ]^{\lambda} \bigl [\rho(s_2) V^{(2)}_i(t) \bigr ]^{1-\lambda} = \rho(s_1)^{\lambda} \rho(s_2)^{1-\lambda} W_i(t)\; . \end{align*} Enfin le théorème 2.4 de (Drnovsek, 2000) (borne supérieure de Collatz et Wielandt) implique que  \(\rho(s)\leq \rho(s_1)^{\lambda} \rho(s_2)^{1-\lambda}\).

    (vii) Supposons qu'il existe \(r_1 < r_2\) avec \(\rho(r_1)=\rho(r_2)=1\).  \(\,s\mapsto \rho(s)\,\) est une fonction décroissante et (log-)convexe. On a donc  \(\rho(s)=1\) pour  \(\,s\geq r_1\). Ceci contredit le fait que  \(\rho(s)\to 0\) si \(s\to +\infty\). Donc il existe un unique \(\,r > -\beta\) avec \(\rho(r)=1\). Il y a deux cas :

• sur l'intervalle \((-\beta,+\infty)\,\), la fonction est strictement décroissante
• sur un intervalle \((-\beta,r_0)\,\), la fonction est strictement décroissante et  \(\rho(s)=0\) si  \(s\geq r_0\).

Appendice 2

    On généralise la preuve de (Michel et coll., 2005) pour le comportement asymptotique d'une population d'un seul type dans un environnement périodique au cas des populations à plusieurs types. Alternativement, ceci peut être vu comme une généralisation aux équations aux dérivées partielles de la remarque 6.2 de (Perthame, 2007) concernant les populations à plusieurs types modélisées par des équations différentielles ordinaires.  \(A'(t,\tau)\), \(B'(t,\tau)\) et  \(K'(t,\tau)\,\) sont les matrices transposées de \(A(t,\tau)\), \(B(t,\tau)\) et  \(K(t,\tau)\). En généralisant le théorème 5.1 de (Michel et coll., 2005), on commence par le lemme suivant:

    Lemme. Il y a un unique triplet \(\,(r,N,\phi)\) solution des problèmes de valeur propre duaux \begin{align} &\frac{\partial N}{\partial t}(t,\tau)+\frac{\partial N}{\partial \tau}(t,\tau) + r\, N(t,\tau) + B(t,\tau) N(t,\tau)=0\; ,\quad \forall t,\ \forall \tau > 0,\tag{23}\\ &N(t,0)=\int_0^\infty A(t,\tau)\, N(t,\tau)\, d\tau\tag{24}\\ &N(t+T,\tau)=N(t,\tau),\quad N(t,\tau)\geq 0,\quad \sum_i \int_0^T \!\! \int_0^\infty \!\! N_i(t,\tau)\, d\tau\, dt=1,\nonumber\\ &\frac{\partial \phi}{\partial t}(t,\tau)+\frac{\partial \phi}{\partial \tau}(t,\tau) -r\, \phi(t,\tau) - B'(t,\tau)\, \phi(t,\tau) =- A'(t,\tau)\, \phi(t,0)\; , \tag{25}\\ &\phi(t+T,\tau)=\phi(t,\tau),\quad \phi(t,\tau)\geq 0,\quad \sum_i \int_0^\infty N_i(t,\tau)\, \phi_i(t,\tau)\, d\tau = 1\; . \nonumber \end{align}

    Preuve. (23)-(24) d'une part et (25) d'autre part se réduisent aux problèmes de valeurs propres duaux \begin{align*} N(t,0)&=\int_0^\infty \!\!\! e^{-r\tau}\, K(t,\tau)\, N(t-\tau,0)\, d\tau\; ,\\ \phi(t,0)&=\int_0^\infty \!\!\! e^{-r\tau} \, K'(t+\tau,\tau)\, \phi(t+\tau,0)\, d\tau, \end{align*} dont les propiétés résultent de l'appendice 1 et du théorème de  \(\text{Krein}\) et Rutman.

    On a le lemme suivant qui généralise l'équation (5.11) de (Michel et coll., 2005) :

    Lemme 5.  \(H:\mathbb{R}\to \mathbb{R}\,\) est une fonction convexe. On supposons que \(\,P(t,\tau)\,\) est solution de (5)-(6). On définit \begin{equation}\tag{26} \mathcal{H}(t)=\sum_i \int_0^\infty \phi_i(t,\tau)\, N_i(t,\tau)\, H \Bigl (\frac{P_i(t,\tau)e^{-r t}}{N_i(t,\tau)}\Bigr ) d\tau. \end{equation} On a alors \[\frac{d\mathcal{H}}{dt}\leq 0,\quad \forall t.\]

    Preuve. Un calcul fastidieux, semblable aux calculs de (Michel et coll., 2005) et (Perthame, 2007), donne \begin{align} \frac{d\mathcal{H}}{dt}=&\sum_{i} \phi_i(t,0)\, N_i(t,0) \Biggl \{ H \Biggl ( \int_0^\infty \!\! \sum_j \mu_{i,j}\, g_j \, d\tau \Biggr ) - \int_0^\infty \!\! \sum_j \mu_{i,j}\, H (g_j)\, d\tau \Biggr \}\nonumber\\ &+ \sum_{i,j} \int_0^\infty \!\! \phi_i\, B_{i,j}\, N_j \Bigl \{ H (g_j) - H(g_i) + (g_i - g_j) H'(g_i) \Bigr \} d\tau\; ,\tag{27} \end{align} avec \begin{equation}\tag{28} \mu_{i,j}(t,\tau)=\frac{A_{i,j}(t,\tau)\, N_j(t,\tau)}{N_i(t,0)}\, ,\quad g_j(t,\tau)= \frac{P_j(t,\tau)\, e^{-r t}}{N_j(t,\tau)}\, . \end{equation} En effet, la dérivée de (26) est \begin{align*} \frac{d\mathcal{H}}{dt}=\sum_i \int_0^\infty \!\! \Bigl \{ &\Bigl [\frac{\partial\phi_i}{\partial t}\, N_i+ \phi_i\, \frac{\partial N_i}{\partial t}\Bigr ] H \Bigl (\frac{P_i\, e^{-r t}}{N_i}\Bigr ) \\ & + \phi_i\, N_i\, H' \Bigl (\frac{P_i\, e^{-r t}}{N_i}\Bigr ) \Bigl [\frac{\partial P_i}{\partial t} -r\, P_i -\frac{P_i}{N_i} \frac{\partial N_i}{\partial t}\Bigr ] \frac{e^{-r t}}{N_i}\Bigr \} d\tau\; . \end{align*} En remplaçant \(\partial P_i/\partial t\), \(\partial N_i/\partial t\) et \(\partial \phi_i/\partial t\) par (5), (23) et (25), on obtient \begin{align*} \frac{d\mathcal{H}}{dt}=\sum_i \int_0^\infty \!\! &\Bigl \{ \Bigl [-\frac{\partial\phi_i}{\partial \tau} +r\, \phi_i + \sum_j \phi_j\, B_{j,i} -\sum_j \phi_j(t,0) A_{j,i} \Bigr ] N_i \, H \Bigl (\frac{P_i\, e^{-r t}}{N_i}\Bigr )\\ & -\phi_i \Bigl [\frac{\partial N_i}{\partial \tau} +r\, N_i + \sum_j B_{i,j}\, N_j \Bigr ] H \Bigl (\frac{P_i\, e^{-r t}}{N_i}\Bigr )\\ & - \phi_i\, N_i\, H' \Bigl (\frac{P_i\, e^{-r t}}{N_i}\Bigr ) \Bigl [\frac{\partial P_i}{\partial \tau} +\sum_j B_{i,j}\, P_j \Bigr ]\frac{e^{-r t}}{N_i}\\ &+ \phi_i\, N_i\, H' \Bigl (\frac{P_i\, e^{-r t}}{N_i}\Bigr ) \frac{P_i}{N_i} \Bigr [\frac{\partial N_i}{\partial \tau}+ \sum_j B_{i,j}\, N_j\Bigr ] \frac{e^{-r t}}{N_i}\Bigr \} d\tau\; . \end{align*} On introduit avec (28) la notation \(g_j\,\). On regroupe les expressions qui contiennent des dérivées par rapport à τ d'un côté, les expressions qui contiennent \(\,B_{i,j}\,\) d'un autre côté. On échange les indices i et j dans les sommes qui contiennent les coefficients \(\,B_{j,i}\) et \(A_{j,i}\). On obtient \begin{align*} \frac{d\mathcal{H}}{dt}=&-\sum_i \int_0^\infty \!\!\! \frac{\partial}{\partial \tau} \Bigl [ \phi_i N_i H (g_i)\Bigr ] d\tau -\sum_{i,j} \phi_i(t,0) \int_0^\infty \!\!\! A_{i,j} N_j H (g_j)\, d\tau\\ &+ \sum_{i,j} \int_0^\infty \!\! \phi_i\, B_{i,j}\, N_j \Bigl \{ H (g_j) - H(g_i) + (g_i - g_j) H'(g_i) \Bigr \} d\tau\; . \end{align*} En intégrant la première intégrale, on arrive à \begin{align*} \frac{d\mathcal{H}}{dt}=&\sum_i \phi_i(t,0) N_i(t,0) \Bigl \{ H (g_i(t,0)) - \int_0^\infty \! \sum_{j} \frac{A_{i,j} N_j}{N_i(t,0)} \, H (g_j)\, d\tau \Bigr \}\\ &+ \sum_{i,j} \int_0^\infty \!\! \phi_i\, B_{i,j}\, N_j \Bigl \{ H (g_j) - H(g_i) + (g_i - g_j) H'(g_i) \Bigr \} d\tau\; . \end{align*} Ceci conduit à (27) si l'on tient compte de la condition au bord (6), qui montre que \[g_i(t,0)=\frac{P_i(t,0)\, e^{-rt}}{N_i(t,0)} = \int_0^\infty \! \sum_j \frac{A_{i,j}(t,\tau)\, N_j(t,\tau)}{N_i(t,0)}\ \frac{P_j(t,\tau)\, e^{-rt}}{N_j(t,\tau)}\, d\tau\; . \]

    Revenons à la preuve du lemme 5. D'après l'inégalité de Jensen avec \(\,\int_0^\infty \bigl (\sum_j \mu_{i,j}\bigr ) d\tau=1\,\), et d'après la version discrète de cette inégalité \[H \Bigl ( \int_0^\infty \!\! \sum_j \mu_{i,j}\, g_j\, d\tau \Bigr ) \leq \int_0^\infty \!\!\! H \Biggl ( \frac{\sum_j \mu_{i,j}\, g_j}{\sum_j \mu_{i,j}} \Biggr ) \Bigl (\sum_j \mu_{i,j}\Bigr ) d\tau\leq \int_0^\infty \!\! \sum_j \mu_{i,j}\, H (g_j)\, d\tau . \] Donc la première ligne dans (27) est négative. La seconde ligne de (27) est aussi négative parce que

• le terme correspondant à i=j s'annule
• pour i≠ j, la convexité de H implique que l'expression à l'intérieur des accolades est positive, tandis que  \(B_{i,j}\leq 0\), \(\phi_i\geq 0\) et \(N_j\geq 0\).

    On arrive ainsi à la généralisation du théorème 5.2 de (Michel et coll., 2005).

    Lemme 6. On suppose

•  \(\,P(t,\tau)\,\) est la solution de (5)-(6) avec la condition initiale \(P(t_0,\tau)\).
•  \(c=\sum_i \int_0^\infty P_i(t_0,\tau)\, \phi_i(t_0,\tau)\, d\tau\).

    Preuve. Noter que \[e^{rt_0} P_i(t,\tau)-c\, N_i(t,\tau)\, e^{rt}\] est aussi une solution des équations linéaires (5)-(6). Avec la fonction convexe \(\,H(x)=|x|\), on applique le lemme 5 à cette solution.  \(\mathcal{H}(t)\,\), le côté droit de (29), décroît avec le temps t et donc converge vers une limite \(\,\ell\). Le fait que  \(\ell=0\) se démontre avec des arguments semblables à ceux de (Michel et coll., 2005, p. 1259) ou (Perthame, 2007, §3.6).

    Corollaire. \(\|P(t,0)\|\sim c\, e^{r(t-t_0)} \| N(t,0)\|\) si \(t\to +\infty\).

Références bibliographiques