Le modèle de Kermack et McKendrick pour la peste à Bombay et la reproductivité d'un type avec saisonnalité

Résumé

La figure montrant comment le modèle de Kermack et McKendrick s'ajuste aux données de 1906 pour l'épidémie de peste à Bombay est l'une des figures les plus reproduites dans les livres sur la modélisation mathématique en épidémiologie. Dans cet article, on montre que l'hypothèse de paramètres constants dans ce modèle conduit à des valeurs numériques irréalistes pour ces paramètres. De plus, les rapports publiés à l'époque montrent que des épidémies de peste se produisaient à Bombay avec une saisonnalité remarquable chaque année à partir de 1897 et au moins jusqu'en 1911. Donc l'épidémie de 1906 n'est vraiment pas un bon exemple d'épidémie s'arrêtant parce que le nombre de personnes susceptibles a baissé sous un certain seuil, comme l'ont suggéré Kermack et McKendrick, mais un exemple d'épidémie saisonnière. On présente un modèle saisonnier pour la peste à Bombay et l'on calcule les reproductivités nettes associées aux rats et aux puces. Ce faisant, on étend aux modèles périodiques la notion introduite par Roberts et Heesterbeek.

1.   Introduction

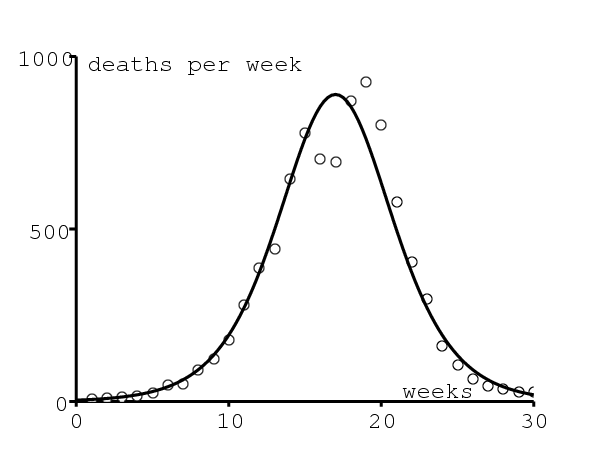
    La figure montrant comment le modèle de Kermack et McKendrick (1927 ; 1991) s'ajuste aux données de 1906 pour l'épidémie de peste à Bombay est bien connue des modélisateurs en épidémiologie (figure 1). Elle a été reproduite dans des livres sur l'épidémiologie mathématique (Keeling et Rohani, 2008 ; Waltman, 1974), la biologie mathématique (Banks, 1994 ; Britton, 2003 ; Cavalli-Sforza et Feldman, 1981 ; Edelstein-Keshet, 2005 ; Hastings, 1997 ; Mangel, 2006 ; Murray, 2002 ; Olinick, 1978 ; Shigesada et Kawasaki, 1997), les équations différentielles (Braun, 1993) et l'histoire de la modélisation mathématique (Bacaer, 2011 ; Israel, 1996). Les données, dont Kermack et McKendrick (1927) ne précisent pas l'origine, viennent d'un rapport d'enquête sur la peste en Inde publié en 1907 (Advisory Committee, 1907b, p. 753).

    Cependant Kermack et McKendrick n'ont pas obtenu la courbe en cloche de la figure 1 directement à partir de leur modèle original, un système de trois équations différentielles, car celles-ci n'avaient pas de solution explicite. Ils ont utilisé à la place une certaine approximation, pour laquelle ils ont obtenu une solution explicite: le nombre de décès par unité de temps  \(dz/dt\) était de la forme \begin{equation}\tag{1} \frac{dz}{dt} \simeq \frac{A}{\cosh^2 (B\, t-\phi )}\; , \end{equation} où les trois paramètres \(A\), \(B\) et  \(\phi\,\) dépendent de manière compliquée des paramètres du modèle. L'ajustement aux données donnait \(\,A=890\) par semaine, \(B=\mbox{0,2}\) par semaine et \(\phi=\mbox{3,4}\). Kermack et McKendrick ont aussi mentionné plusieurs hypothèses simplificatrices de leur modèle; par exemple, leur modèle ne tient pas compte explicitement des rats et des puces qui transmettent la peste. Ils ont remarqué que:

« None of these assumptions are strictly fulfilled and consequently the numerical equation can only be a very rough approximation. A close fit is not to be expected, and deductions as to the actual values of the various constants should not be drawn. »

    Malgré cette mise en garde, il peut être intéressant d'étudier cela de plus près. En particulier, on peut se demander:

• Quelles sont les valeurs des paramètres du modèle original qui correspondent à l'ajustement de la figure 1?
• Quelle est la reproductivité  \(R_0\)  associée?

    Dans la section 2, on rappelle le contexte historique et les formules obtenues par Kermack et McKendrick. Dans la section 3, on présente les calculs qui permettent de retrouver les valeurs des paramètres à partir de l'ajustement, on les appliquent au cas de la peste à Bombay et l'on explique que les valeurs obtenues sont assez irréalistes. Il faut donc remettre en cause l'hypothèse des valeurs constantes pour les paramètres. La section 4 discute du rôle de la saisonnalité, qui est sûrement responsable du déclin de l'épidémie en 1906, et propose un modèle périodique pour cette épidémie de peste. Le modèle comprend les puces, les rats et les humains comme dans (Keeling et Gilligan, 2000 ; Keeling et Gilligan, 2000 ; Monecke et coll., 2009). Noter cependant que (Monecke et coll., 2009) ne considère que des épidémies d'une année sans tenir compte de la saisonnalité. Un des modèles dans (Keeling et Gilligan, 2000) était saisonnier mais regardait à l'échelle du siècle, de sorte que

« the effects of the seasonal fluctuations are averaged out. »

2.   La peste bubonique à Bombay et les formules obtenues par Kermack et McKendrick

    La peste bubonique apparut à Bombay, désormais Mumbai, en août 1896 (Gatacre, 1897). Elle devint endémique en réapparaissant les années suivantes avec un fort caractère saisonnier comme on va le voir dans la section 4. La peste se répandit aussi à travers l'Inde, ce qui causa plus de dix millions de morts entre 1898 et 1918 (Pollitzer, 1954, p. 26). En janvier 1905, le secrétaire d'état aux Indes, la Royal Society et l'institut Lister créèrent un comité consultatif. Sa commission de travail était basée à Bombay. La commission fit de nombreuses expériences de laboratoire et études de terrain pour étudier tous les aspects de la maladie. En conséquence, pas moins de quatre-vingt-quatre « Rapports d'étude sur la peste en Inde », avec des centaines de tableaux, de diagrammes et de cartes, furent publiés entre septembre 1906 et avril 1917 comme numéros spéciaux du  \(\text{Journal of Hygiene}\). Ce journal a maintenant été numérisé et qui est accessible gratuitement sur www.ncbi.nlm.nih.gov/pmc/journals/326/. La plupart des informations de notre article viennent de ces rapports.

    L'épidémie saisonnière de peste de 1906, qui dura de janvier à juillet 1906, fut la première épidémie que la commission étudia et aussi celle qui reçut la plus grande attention. Mais en réalité elle fut d'une « sévérité modérée ». La commission fut capable d'établir définitivement le rôle des rats et de leurs puces dans la propagation de la peste. On peut noter que M. Kesava Pai, avec lequel McKendrick allait écrire un article en 1911, et le directeur de l'Institut Pasteur de l'Inde à Kasauli, où McKendrick allait travailler entre 1905 et 1920, étaient membres de la commission.

    Dans (Kermack et McKendrick, 1927), Kermack et McKendrick étudièrent un modèle mathématique avec trois compartiments:  \(x(t)\) personnes saines, \(y(t)\) personnes infectées par la peste et \(z(t)\,\) personnes mortes ou immunisées. Les équations étaient \begin{equation}\tag{2} \frac{dx}{dt}=-k\, x \, y,\quad \frac{dy}{dt}=k\, x \, y - \ell \, y,\quad \frac{dz}{dt}=\ell\, y\; . \end{equation}  \(k > 0\) est une sorte de taux de contact et  \(\ell > 0\,\) une mortalité ou un taux de guérison. Les auteurs purent montrer que si les conditions initiales sont \(\,x(0)=x_0\), \(y(0)=y_0\) et \(z(0)=0\,\), \[\frac{dz}{dt}=\ell \Bigl ( x_0+y_0 - x_0\, e^{-k z/\ell} - z\Bigr ),\] une équation qui ne semble pas avoir de solution explicite. Ils supposèrent que l'expression sans dimension \(\,k\, z(t)/\ell\) reste relativement petite et utilisèrent l'approximation \(e^{-u}\simeq 1-u+u^2/2\) pour obtenir \[\frac{dz}{dt}\simeq \ell \Bigl [y_0 + \Bigl (\frac{k\, x_0}{\ell} - 1\Bigr )z - \frac{x_0\, k^2}{2\, \ell^2}\, z^2\Bigr ]\; .\] Cette équation de Riccati a une solution explicite \(z(t)\) qui donne un nombre de décès par unité de temps égal à (1), où \[A=\frac{\ell^3\, Q^2}{2 \, x_0\, k^2} ,\ B= \frac{Q\, \ell}{2},\ \tanh(\phi) = \frac{\frac{k\, x_0}{\ell} - 1}{Q}\; ,\ Q=\sqrt{\Bigl (\frac{k\, x_0}{\ell} -1 \Bigr )^2 + 2\, x_0\, y_0 \, \frac{k^2}{\ell^2}}\, . \] Noter avec (1) que \(A\) est le maximum de \(dz/dt\) (environ 900 par semaine dans la figure 1) et que \(t^*=\phi/B\,\) est l'instant où le maximum est atteint (19 semaines après le début dans la figure 1). Donc il n'y a réellement qu'un seul paramètre inconnu dans le processus d'ajustement, disons B, et Kermack et McKendrick ont probablement essayé plusieurs valeurs. Après une première estimation de B, ils se sont probablement rendus compte que leur ajustement à la courbe entière pouvait être amélioré en changeant légèrement les paramètres : A=890 par semaine et \(\,t^*=\phi/B=17\,\) semaines. Finalement, ils optèrent pour  \(B=\mbox{0,2}\) par semaine et donc  \(\phi=\mbox{3,4}\). Cependant le modèle a quatre paramètres : \(\,x_0\), \(y_0\), \(k\) et \(\ell\). Comment déduire quatre paramètres inconnus de seulement trois équations?

3.   Les valeurs des paramètres

    Avec \(R=k x_0/\ell\,\), on a \[A= \frac{\ell\, Q^2\, x_0}{2\, R^2},\quad B= \frac{Q\, \ell}{2},\quad \tanh(\phi)=\frac{R-1}{Q},\quad Q=\sqrt{(R-1)^2+2\, R\, y_0/x_0}\; .\] Donc \(Q=(R-1)/\tanh(\phi)\) et \begin{equation}\tag{3} x_0= \frac{2\, R\, y_0}{Q^2-(R-1)^2}=\frac{2\, R\, y_0}{(R-1)^2(\frac{1}{\tanh^2(\phi)}-1)}=\frac{2\, R\, y_0\, \sinh^2(\phi)}{(R-1)^2} \, . \end{equation} Mais les équations pour \(A\) et \(B\) indiquent aussi que \(\ell=2B/Q\) et \begin{equation}\tag{4} x_0=\frac{2R^2 A}{\ell Q^2}=\frac{R^2 A}{B Q}=\frac{R^2 A \tanh(\phi)}{B (R-1)}=\frac{R^2 A \sinh(\phi)}{B (R-1) \cosh(\phi)} \, . \end{equation} Avec les équations (3) et (4), on obtient \begin{equation}\tag{5} R(R-1)=\frac{2\, B\, y_0\, \sinh(\phi)\, \cosh(\phi)}{A} = \frac{B\, y_0\, \sinh(2\phi)}{A}\; . \end{equation} La seule racine positive de cette équation quadratique en R est \begin{equation}\tag{6} R = \frac{1+\sqrt{1+4 B\, y_0\, \sinh(2\phi)/A} }{2}\; . \end{equation}

    Nous avons quatre inconnues mais trois équations. Plusieurs choix pour les paramètres \(\,(x_0,y_0,k,\ell)\) correspondent au même triplet \((A,B,\phi)\). On pourrait décider de fixer l'un des paramètres: la période infectieuse moyenne de la peste \(\,1/\ell\), la taille initiale \(x_0\) de la population saine à Bombay en 1905 ou le nombre initial de personnes infectées  \(y_0\). Il ne semble pas possible de fixer k a priori.

    On pourrait croire d'abord que le choix de la période infectieuse est relativement simple. D'après (Advisory Committee, 1907b, p. 765), la durée moyenne de la maladie dans les cas fatals est d'environ \(\,\mbox{5,5}\,\) jours. Cependant il y a aussi une période d'incubation d'environ 3 jours en moyenne (Advisory Committee, 1907b, p. 765). Enfin on ne devrait pas oublier que le modèle (2) est une simplification du processus d'infection. Les rats infectés infectent leurs puces, qui infectent d'autres rats et à l'occasion aussi des humains. L'épidémie de peste chez les humains est complètement déterminée par l'épizootie chez les rats, avec juste quelques jours de retard (Advisory Committee, 1907b, figure III).

    Imaginons alors que le système (2) soit un modèle pour la peste chez les rats. Dans des expériences de laboratoire, les rats de Bombay auxquels la peste a été effectivement transmise mouraient en moyenne 9 jours après leur première exposition à des puces infectées (Advisory Committee, 1906a, p. 445). Mais encore une fois, on ne devrait pas oublier que cette durée peut ne pas avoir grand chose à voir avec la « période infectieuse apparente » puisque les puces quittent les rats seulement quand ils sont déjà morts. D'après (Advisory Committee, 1908, p. 285), des expériences ont montré que les puces peuvent rester infectieuses deux semaines pendant la saison de la peste mais seulement une semaine en dehors de cette saison. Il y a donc des variations saisonnières considerables, sur lesquelles on reviendra dans la section 4. Par conséquent, dans le cadre d'un modèle autonome aussi simple que (2), le choix de \(\,1/\ell\) n'est pas simple.

    Considérons maintenant la taille initiale  \(x_0\,\) de la population saine à Bombay en décembre 1905. à cette époque, la population de Bombay était presque entièrement concentrée sur « l' île de Bombay » et ses 22 miles carrés. Le recensement de février 1906 donna une population d'environ un million d'habitants (Advisory Committee, 1907b, p. 726). On choisit  \(x_0=10^6\). L'équation (4) montre que  \(R\) est solution de l'équation quadratique \[(A \tanh \phi) R^2 - (B x_0) R + B x_0=0.\] Numériquement, on obtient  \(R\simeq 202\) et \(R\simeq \mbox{1,005}\). Mais (5) montre que  \(y_0=AR(R-1)/(B\sinh(2\phi))\). Cela donne  \(y_0\simeq \mbox{446 000}\) et  \(y_0\simeq \mbox{0,06}\). les deux solutions sont absurdes, la première parce que l'épidémie de 1906 tua environ 10000 personnes, la deuxième parce que  \(y_0\,\) est un nombre de personnes. Ainsi il n'est pas possible de prendre la population entière comme population à risque.

    Il reste à vérifier si l'on obtient des valeurs réalistes pour les paramètres avec un choix de \(y_0\). Posons par exemple \(\,y_0=1\,\) au début de la courbe épidémique. En fait, (Kermack et McKendrick, 1927) (voir figure 1) ne précise pas à quel événement correspond l'instant \(\,t=0\). Une fois choisi  \(y_0\,\), l'équation (6) donne \(R\). On peut calculer \(\,Q=(R-1)/\tanh(\phi)\) et  \(\ell=2B/Q\). Finalement \(\,x_0\) est donné par (3) et  \(k=R\, \ell/x_0\). Avec  \(y_0=1\,\), on obtient \(\ell\simeq \mbox{4,32}\) par semaine, \(x_0\simeq \mbox{57 368}\) et  \(k\simeq \mbox{0,0000823}\,\) par semaine. Noter que la période infectieuse moyenne serait de  \(1/\ell\simeq \mbox{0,23}\) semaine, c'est-à-dire  \(\mbox{1,6}\,\) jours. La population à risque serait \(\,N=x_0+y_0\simeq \mbox{57 369}\). La reproductivité serait \(\,R_0=kN/\ell\simeq \mbox{1,09}\) et numériquement presque égale à \(R\). Ce \(\,R_0\) semble assez petit en comparaison avec les valeurs typiques pour d'autres maladies infectieuses (Anderson et May, 1991 ; Keeling et Rohani, 2008, p. 21), en particulier vu que l'épidémie de peste n'est pas due à un lent accroissement de la densité de population jusqu'au seuil  \(R_0=1\,\) mais presque sûrement à l'arrivée par b\^ateau de rats infectés. La troisième pandémie de peste a commencé en 1894 à Hong Kong. Cependant, comme la « période infectieuse apparente »  \(1/\ell\) (dont l'interpretation est difficile, comme on l'a vu ci-dessus) est aussi très courte, le temps de doublement  \(\log(2)/(kx_0-\ell)\,\) au début de l'épidémie prend une valeur raisonnable, environ 13 jours. Un problème plus grand survient quand on considère la population à risque \(\,N\simeq \mbox{57 000}\). Avec les rapports sur la distribution géographique des cas de peste chez les humains (Advisory Committee, 1907b, carte I, p. 727 et p. 787-794), il semblerait que toutes les zones densément peuplées de l'île de Bombay furent touchées par l'épidémie. Il n'y a pas de raison évidente pour que seules 57000 personnes soient à risque lorsque la population totale est d'environ un million.

    On pourrait se demander si un choix légèrement différent de \(y_0\,\) (supposé être un entier) pourrait conduire à des valeurs de paramètres plus raisonnables. C'est ce que montre le tableau 1, où l'on inclut \(\,R_0\) plutôt que  \(k\). Les courbes épidémiques correspondantes (non représentées) restent toutes proches de celle de la figure 1, mais l'approximation se détériore à mesure que  \(y_0\) augmente.

    Le tableau 1 semble suggérer que notre processus d'estimation n'est pas vraiment robuste. Mais souvenons-nous que \(\,R_0\,\) est supposé être juste au-dessus de 1, là où le modèle est très sensible à de petits changements dans les valeurs des paramètres. Dans tous les cas, les différentes valeurs de \(\,x_0\) et \(N=x_0+y_0\) dans le tableau 1 sont toutes beaucoup trop petites pour être réalistes.

    Jusqu'à présent on a supposé implicitement que toutes les infections conduisent au décès. Mais (Advisory Committee, 1907b, p. 762) mentionne 11010 morts parmi 12245 infections, soit 90% de mortalité. Parce que \(\,z(t)\) inclut à la fois les morts et les guéris, la courbe pour \(dz/dt\) (figure 1) doit être remise à l'échelle avec un nouveau maximum \(A\) égal à \(890/90\%\simeq 989\), les paramètres \(B\) et \(\phi\,\) restant identiques. Avec \(\,y_0=1\), les nouveaux paramètres sont  \(x_0\simeq \mbox{69 183}\), \(1/\ell\simeq \mbox{1,5}\) jours et \(R_0\simeq \mbox{1,08}\). Il y a peu de différence avec le cas où il y a 100% de mortalité. la population estimée à risque reste trop petite.

    En résumé, il semble que l'ajustement à la courbe épidémique sous l'hypothèse de paramètres constants conduit à des valeurs des paramètres irréalistes. Il n'est pas suffisant, comme l'écrivent Kermack et McKendrick (1927, p. 715), que

« the calculated curve, which implies that the rates did not vary during the period of epidemic, conforms roughly to the observed figures. »

4.   La saisonnalité

    La solution du problème de la section précédente est en fait très simple. Le modèle (2) doit être abandonné. On peut obtenir la courbe de la figure 1 avec des valeurs des paramètres plus réalistes en incluant la saisonnalité. Notre objectif est désormais de développer un modèle saisonnier réaliste de l'épidémie de peste et d'estimer la reproductivité correspondante. On inclura les deux hôtes principaux, les rats et les puces, pour lesquels la reproductivité d'un type, T, est une meilleure mesure de l'effort nécessaire pour contrôler l'épidémie. On discutera donc aussi du calcul de T pour les modèles saisonniers, ce qui peut être d'un intérêt plus large.

    La peste apparut à Bombay en août 1896 mais la première vraie épidémie commença au printemps 1897. Elle devint endémique. Des décès dûs à la peste furent enregistrés presque tous les mois au moins jusqu'en 1911, avec des pics en mars ou avril de chaque année (figure 2). Une mortalité élevée s'observa invariablement entre décembre et juin, une faible mortalité entre juillet et novembre. La peste demeura fréquente à Bombay jussqu'en 1923 (Pollitzer, 1954, p. 28). Ce caractère saisonnier régulier est très différent des épidémies de peste du 14e au 18e siècle en Europe, qui se produisirent de manière irrégulière et furent le sujet des modèles antérieurs (Keeling et Gilligan, 2000 ; Keeling et Gilligan, 2000 ; Monecke et coll., 2009).

    (Advisory Committee, 1908 ; St John Brooks, 1917) ont étudié l'origine de cette saisonnalité. Une comparaison avec les statistiques météorologiques montra que l'épidémie ne pouvait se maintenir quand la température moyenne était au dessus de 80°F, soit 26,7°C. Une conclusion similaire fut obtenue pour d'autres régions de l'Inde, avec l'humidité qui joue un rôle secondaire (St John Brooks, 1917). Les bacilles de la peste sont sensibles à la température. Des expériences de laboratoire montrèrent que la proportion de puces dans l'estomac desquelles se produit une multiplication abondante des bacilles de la peste pouvait être plusieurs fois supérieure par temps frais que par temps chaud (Advisory Committee, 1908, p. 283-285). Corrélativement, des puces pouvaient restées infectieuses bien plus longtemps par temps frais que par temps chaud. Des résultats similaires furent obtenus en utilisant une chambre froide ou une chambre chauffée.

    Un autre facteur était la présence saisonnière des puces des rats. On put en capturer plus, en utilisant des cochons d'Inde comme appâts, entre janvier et mars que pendant les autres mois de l'année (Advisory Committee, 1908, p. 296). Le nombre moyen de puces trouvées sur les rats capturés entre février et mai fut aussi le plus élevé (Advisory Committee, 1908, p. 297). Cependant les variations dans l'abondance des puces pouvaient être dues aux puces qui quittent les rats morts de la peste pour trouver un nouvel hôte.

    La saisonnalité de la fertilité des rats, estimée par la fraction de jeunes rats et de rattes en gestation parmi les rats capturés, sembla moins important (Advisory Committee, 1907b, p. 748). Cependant les populations de rats ont certainement oscillé à cause de la mortalité due à la peste.

    Avec tous ces éléments, il est clair que le déclin de l'épidémie de 1906 en juin ne doit pas être attribué à la baisse du nombre de personnes saines sous un certain seuil, comme le suggère le modèle de Kermack et McKendrick, mais simplement à un facteur saisonnier touchant les bacilles et les puces. Comme modèle alternatif, on pourrait essayer de garder les mêmes équations (2) mais avec des coefficients périodiques. Mais à ce stade, un modèle légèrement plus complexe et plus réaliste semble approprié. On utilisera la notation désormais standard  \((S,I,R)\) au lieu de \((x,y,z)\).  \(S(t)\) est le nombre de rats sains, \(I(t)\) le nombre de rats infectés et \(R(t)\) le nombre de rats immunisés.  \(P(t)=S(t)+I(t)+R(t)\,\) est le nombre total de rats en vie. De manière plus précise, on ne considérera que le rat noir, quoique les rapports indiquent clairement que l'épizootie de peste parmi ces rats était toujours précédée, avec seulement quelques semaines de différence, par une épizootie similaire parmi les rats bruns. \(\,F(t)\) est le nombre de puces infectées vivant librement, c'est-à-dire qui ne sont pas encore fixées sur un rat ou sur un humain. \(H(t)\) est le nombre d'humains infectés.  \(D(t)\,\) est l'incidence des décès dûs à la peste chez les humains. On ne tient pas compte des humains sains et des puces saines car ils étaient probablement très en excès: rappelons qu'il y eut annuellement environ 10000 décès dûs à la peste chez les humains dans une population d'un million. Comme la peste bubonique est principalement une épizootie parmi les rats, les humains n'étant qu'un hôte occasionnel des puces des rats, on tient compte du nombre de rats susceptibles et immunisés. On résume le processus d'infection ainsi: \begin{align} &\frac{dS}{dt} = b(P) - m\, S - c\, (1-\omega)\, \pi(\theta(t))\, \frac{S}{P}\, F + \varepsilon\, m'\, I,\tag{7}\\ &\frac{dI}{dt} = c\, (1-\omega)\, \pi(\theta(t))\, \frac{S}{P}\, F - m'\, I,\tag{8}\\ & \frac{dR}{dt}=\varepsilon'\, m'\, I - m\, R,\\ &\frac{dF}{dt}=f\, \pi' (1-\varepsilon-\varepsilon') m'\, I - c\, F,\tag{9}\\ & \frac{dH}{dt}=c \, \omega\, \pi(\theta(t))\, F - a\, H,\quad \quad D(t) = \sigma\, a \, H(t).\tag{10} \end{align} Le tableau 2 donne la signification des paramètres et leurs valeurs numériques.

    Voici quelques commentaires sur le modèle et sur les paramètres:

• Le lecteur peut remarquer la similitude entre le présent modèle et des modèles intra-hôtes pour l'infection par le VIH, les rats infectés libérant les puces quand ils meurent comme les cellules CD4 infectées libèrent les virions du VIH quand elles explosent (Nowak et May, 2000).
• Le modèle convient pour la peste bubonique, de loin la plus fréquente en Inde (Pollitzer, 1954, p. 28), mais bien sûr pas pour la peste pulmonaire, qui fut la forme principale de l'épidémie à Harbin (Dietz, 2009). La peste pulmonaire peut se transmettre directement entre humains.
• Des expériences de laboratoire ont montré que la transmission directe de la peste bubonique ne peut se produire en l'absence de puces (Advisory Committee, 1906a, p. 466).
• Les données de l'article classique de P.H. Leslie (1945) concernent le rat brun (noter que \(\log(2)/m\simeq 23\,\) mois est la demi-vie). Cependant des élevages expérimentaux de rats noirs, dont la population croît comme \(\,e^{(r-m)t}\,\), donnèrent des résultats similaires (Advisory Committee, 1911, p. 199). Le paramètre K dans l'expression de \(\,b(P)\), qui est lié à la taille de la population de rats, est un paramètre libre que l'on a utilisé pour l'ajustement à la courbe de la peste chez les humains.
• On a pris pour le temps moyen nécessaire aux puces pour trouver un hôte  \(1/c\simeq 1\,\) jour, à cause de l'observation suivante: « in a building in Bombay, in which there had been a severe rat mortality, proved to be due to plague, we had taken rat fleas in large numbers on the legs of men who entered some of the rooms in this building even for a short time (Advisory Committee, 1907a, p. 475). Prendre  \(1/c\simeq \mbox{0,5}\) jour ne fait presque pas de différence (voir aussi la section 6 ci-dessous).
• La proportion  \(\omega\)  de puces libres qui trouvent un hôte humain dépend des conditions sanitaires à Bombay (Advisory Committee, 1907b). On l'a utilisé comme un paramètre à ajuster, en notant que le nombre de décès dûs à la peste est presque proportionnel à ω.
• La probabilité de transmission  \(\pi(\theta)\)  modélise la dépendance à la température du développement des bacilles dans l'estomac des puces. On a choisi une fonction lisse avec un seuil relativement marqué à 80°F de sorte que, comme l'indique (Advisory Committee, 1908, p. 283), les puces sont à peu près deux fois moins susceptibles de transmettre la peste lorsqu'il fait chaud que lorsqu'il fait frais. Le maximum de la probabilité de transmission  \(\pi_0\,\) est un paramètre libre que l'on a utilisé pour ajuster la courbe de la peste chez les humains. (Gatacre, 1897, p. 11) mentionne une probabilité de transmission par piqûre inférieure à 15% ; noter cependant que  \(\pi(\theta)\) est la probabilité de transmission globale, ce qui implique les multiples piqûres de la puce sur son rat hôte.
• La figure 3 montre la température moyenne enregistrée à Bombay de janvier 1897 à décembre 1906 avec un pas de temps de deux semaines. Elle est proche d'une fonction périodique. Pour notre modèle, on fait l'hypothèse simplificatrice que  \(\theta(t)\) est une vraie fonction périodique avec une période \(\tau=1\) an et avec des valeurs obtenues en moyennant les dix années de données de la figure 3. Noter qu'il n'y a pas de corrélation évidente entre la déviation de la température mensuelle par rapport à sa moyenne et les variations en taille des pics des épidémies saisonnières de la figure 2.
• Les proportions \(\varepsilon'\) et  \(\varepsilon\,\) de rats infectés qui survivent à la peste avec ou sans immunité ne sont pas faciles à estimer puisque nombre de rats utilisés dans les expériences de laboratoire étaient déjà immunisés. Mais des expériences similaires, faites sur des cochons d'Inde non immunisés avec des conditions de température favorables, suggèrent que 10 à 20% pouvaient survivre (Advisory Committee, 1908, p. 283\(-\)284). Pour simplifier, on a supposé que \(\,\varepsilon=\varepsilon'=10\%\). De cette manière, un rat infecté qui survit à la peste a 50% chance d'être immunisé.
• Le nombre de puces trouvées sur des rats noirs varie de manière saisonnière (Advisory Committee, 1907b, p. 752 ; voir aussi (Otten, 1932) pour des données de Java). On n'a gardé que la moyenne \(f\simeq 4\) puces par rat.
• Le rat étant un animal à sang chaud, on a supposé que la probabilité de transmission de la peste du rat à la puce ne dépend pas de la température extérieure et est égale au maximum de la probabilité de transmission de la puce au rat :  \(\pi'=\pi_0\).

    En résumé, on a gardé trois paramètres libres principaux (\(K\), \(\omega\) et \(\pi_0\)) pour ajuster le nombre de décès dûs à la peste. On a ajusté ces paramètres par tatonnement pour obtenir un nombre maximum de décès inférieur à 1000 par semaine, pour avoir un pic épidémique en mars ou avril, et pour avoir une épidémie saisonnière qui dure environ 5 mois. On a finalement choisi : \(K=\mbox{50 000}\), \(\omega=2\%\) et \(\pi_0=90\%\). La population de rats noirs en l'absence de peste est ainsi \(\,S^*=K(r/m-1)\simeq \mbox{620 000}\,\), c'est-à-dire moins d'un rat noir par habitant. Avec notre choix des valeurs des paramètres et avec un rat infecté introduit début août 1896, le modèle (7)-(10) converge vers une solution périodique, que l'on compare avec les données pour les années 1904-1907 dans la figure 4.

    La sortie du modèle ne peut s'ajuster à toute la série temporelle de la figure 2, et cela pour les raisons suivantes. Le premier pic épidemique produit par le modèle après l'introduction d'un cas infecté est plusieurs fois plus grand que les pics des années suivantes puisque tous les rats sont sains au départ. Ce n'est pas ce qu'on observe dans la figure 2. On trouve de possibles explications dans un rapport sur la peste à Bombay (Gatacre, 1897) publié en 1897, c'est-à-dire une année après le début de l'épidémie et plusieurs années avant la création du comité consultatif et de la commission de travail. Le rapport explique en détail les difficultés pour arriver à des estimations fiables de la mortalité due à la peste pendant la première année de l'épidémie: certains mois, il fut estimé que les décès comptabilisés comme dûs à la peste (figure 2) étaient inférieurs au tiers de l'excédent de mortalité calculé en soustrayant la mortalité moyenne des années précédentes à la mortalité totale observée pendant l'épidémie (Gatacre, 1897, p. 2). Au contraire, le rapport publié dix ans plus tard en 1907 est très confiant dans les statistiques sur la peste car l'identification des cas de peste était devenue routinière (Advisory Committee, 1907b, p. 728-734). Ainsi la taille des premiers pics épidémiques dans la figure 2 est douteuse. Un autre facteur important est la baisse de la population de 850000 à 437000 entre décembre 1896 et février 1897; les gens avaient fuit Bombay pour échapper à la peste (Gatacre, 1897, p. 251). Cette migration, considérée alors comme « probably unique in the history of the world », a certainement diminué la taille du premier pic épidémique. La population retourna à son niveau normal quelques mois apès le premier pic (Gatacre, 1897, plan 3). Enfin il se peut que les pics épidémiques plus petits après 1907 (figure 2) soient dûs aux interventions efficaces suggérées par la commission après avoir soigneusement compris l'épidémiologie de la peste. Tout ceci tend à justifier pourquoi la figure 4 ne se concentre que sur la période 1904-1907.

    La figure 5 montre les oscillations périodiques de la population de rats. Noter que, comparé avec la situation sans maladie, la peste a divisé environ par 5 la population totale de rats. La population de rats susceptibles est aussi très réduite pendant la saison de la peste de février à avril mais commence à croître à la fin avril lorsque des températures plus élevées réduisent la transmission. Cet accroissement continue jusqu'au mois de janvier suivant. Le nombre de rats sains et les conditions de température sont alors favorables à une nouvelle épidémie. Le nombre minimum de rats infectés pendant une saison est 26, ce qui est beaucoup trop petit pour être visible sur la figure 5 mais probablement suffisant pour éviter l'extinction si la stochasticité était prise en compte. La proportion de rats immunisés R/P varie entre 25% en février au début de l'épizootie saisonnière et 65% en mai à la fin de l'épizootie. Ces changements de l'immunité se voyaient également dans les expériences de laboratoire (Advisory Committee, 1908, p. 292). Enfin l'on peut noter que, contrairement au modèle de (Monecke et coll., 2009) où les puces étaient supposées ne chercher des humains qu'après la réduction drastique de la population de rats (voir en particulier (Monecke et coll., 2009, figure 3), l'épidémie dans la figure 4 et l'épizootie dans la figure 5 se recouvrent largement, la première n'ayant que quelques semaines de retard par rapport à la seconde. Ceci se confirme sur les données concernant le nombre de rats noirs infectés (vivants ou morts) examinés à Bombay en 1905-1906 (Advisory Committee, 1907b, figure III).

    Bien sûr, comme dans le modèle SIR classique avec une démographie périodique, le modèle (7)-(10) a aussi des solutions sous-harmoniques et peut-être aussi des solutions chaotiques pour des valeurs des paramètres différentes. On n'a pas essayé de tracer de diagramme de bifurcation. Cette complexité potentielle peut expliquer en partie pourquoi les pics épidémiques saisonniers dans la figure 2 ne sont pas tous de la même taille. L'idée ici était juste de montrer qu'un modèle saisonnier pouvait s'ajuster aux données avec des valeurs des paramètres réalistes, contrairement à (Kermack et McKendrick, 1927).

5.   La reproductivité d'un type avec de la saisonnalité

    Tournons-nous maintenant vers la seconde question posée dans l'introduction: quelle est la reproductivité associée à la peste à Bombay? On utilisera le modèle périodique de la section précédente, qui comprend les rats et les puces. Comme Roberts et Heesterbeek l'ont remarqué pour les maladies infectieuses avec plus d'un animal hôte (Heesterbeek et Roberts, 2007 ; Roberts et Heesterbeek, 2003 ; Roberts, 2007), il vaut mieux calculer ce qu'ils appellent la reproductivité pour chaque type d'hôte différent. Rappelons tout d'abord quelques généralités concernant la reproductivité d'un type dans un environnement constant avant d'étendre la notion aux modèles périodiques.

5.1   Environnement constant

    Considérons un modèle autonome linéarisé avec n états infectés \(\,dJ/dt = (A- B) J(t)\), avec

•  \(J(t)=(J_1(t),\ldots,J_n(t))^{T}\),
• A est une matrice de transmission dont les éléments sont tous ≥0,
• B est une matrice de transition qui est une M-matrice inversible (Berman et Plemmons, 1994 ; van den Driessche et Watmough, 2002).

• B (ou sa matrice transposée \(\,B^{T}\)) est une M-matrice inversible;
• toutes les valeurs propres de B ont une partie réelle  \( > 0\) 
•  \(\exists\, d_1 > 0,\ldots,d_n > 0\) avec  \(d_j\, B_{j,j} > \sum_{i\neq j} d_i\, |B_{i,j}|\ \forall j\) 
• B est inversible et \(\,B^{-1}\) est une matrice positive (Berman et Plemmons, 1994, p. 134-137).

    Supposons maintenant que le contrôle se fasse sur un sous-ensemble non vide \(\mathcal{E}\subset \{1,\ldots,n\}\,\) de tous les états infectés. Comme dans (Roberts et Heesterbeek, 2003), on définit

• P : la matrice de projection sur ce sous-ensemble, avec \(\,P_{i,j}=0\) si \(i\neq j\), \(P_{i,j}=0\) si \(i=j\notin \mathcal{E}\,\), et \(P_{i,i}=1\) si \(i\in \mathcal{E}\) 
•  \(\mathcal{I}\,\) : la matrice identité de taille n
•  \(\widehat{A}=PA\) et \(A^*=(\mathcal{I}-P)A\).

pour le modèle (A,B), la reproductivité d'un type associé à \(\,\mathcal{E}\) est la reproductivité du modèle  \((\widehat{A},\widehat{B})\).

    Pour les modèles en temps discret de la forme  \(J(t+1)=(A+B)J(t)\) avec des matrices positives \(A\) et \(B\) avec \(\rho(B) < 1\) (voir par exemple (Bacaër, 2009)), on a \(R_0=\rho(K)\) avec \(K=A(\mathcal{I}-B)^{-1}\). Un calcul semblable montre une nouvelle fois que \[T=\rho(PA(\mathcal{I}-(\mathcal{I}-P)A-B)^{-1})=\rho \bigl (PK(\mathcal{I}-(\mathcal{I}-P)K)^{-1}\bigr ).\]

5.2   Environnement périodique

    Considérons maintenant un système linéarisé périodique de période τ \[\frac{dJ}{dt} = (A(t)- B(t)) J(t),\] que l'on appelle le modèle \((A(t),B(t))\).

•  \(A(t)\) est une matrice de transmission continue positive
•  \(B(t)\) est une matrice de transition continue avec des éléments hors diagonale qui sont \(\leq 0\).

    Noter que si  \(B(t)\) est constant et égal à B, alors \(\,\rho(X(\tau))=\rho(\exp(-\tau B)) < 1\,\) si et seulement si toutes les valeurs propres de B ont une partie réelle >0, autrement dit, si B est une M-matrice inversible.

    Retournons au cas périodique. Considérons, comme ci-dessus, un sous-ensemble \(\,\mathcal{E}\)  de \(\{1,\ldots,n\}\,\) et la matrice de projection P qui lui correspond. On définit

•  \(\widehat{A}(t)=PA(t)\) 
•  \(A^*(t)=(\mathcal{I}-P)A(t)\)
•  \(\widehat{B}(t)=B(t)-A^*(t)\).

la reproductivité d'un type associée à  \(\mathcal{E}\) dans le modèle  \((A(t),B(t))\) est la la reproductivité du modèle  \((\widehat{A}(t),\widehat{B}(t))\).

    En fait, comme le signale (Thieme, 2009), une formule de la forme \(R_0=\rho(\mathcal{A} \mathcal{B}^{-1})\) reste vraie dans le cas particulier des équations différentielles périodiques, avec \((\mathcal{A}u)(t)=A(t)u(t)\) et \((\mathcal{B}u)(t)=\frac{du}{dt}+B(t)u(t)\) pour toute fonction périodique de période τ, \(u(t)\). Les coefficients hors diagonale ≤ 0 de  \(B(t)\) et la condition \(\rho(X(\tau)) < 1\) assurent que \(\mathcal{B}\) est inversible et que son inverse est un opérateur positif (par exemple, \((\mathcal{B}^{-1}u)(t)=\int_0^\infty \exp(-\int_{t-x}^t B(y)\, dy)\, u(t-x)\, dx\) si \(B(t)\) est une fonction scalaire). Donc une formule pour T semblable à (11) reste vraie, sauf qu'elle ne semble pas être d'utilité pratique.

    Pour les modèles périodiques de période τ en temps discret \[J(t+1)=(A(t)+B(t)) J(t)\] avec des matrices positives \(A(t)\) et \(B(t)\) et \(\rho(B(\tau-1)\cdots B(1) B(0)) < 1\) comme dans (Bacaër, 2009), la reproductivité d'un type est encore donnée par la reproductivité du modèle équivalent \(J(t+1)=(\widehat{A}(t)+\widehat{B}(t)) J(t)\), avec \(\widehat{A}(t)=PA(t)\), \(\widehat{B}(t)=(\mathcal{I}-P)A(t)+B(t)\), et pourvu que \(\rho(\widehat{B}(\tau-1)\cdots \widehat{B}(1) \widehat{B}(0)) < 1\).

    Enfin, pour les modèles périodiques structurés par le temps \(x\) écoulé depuis l'infection, qui sont de la forme \begin{align} &\frac{\partial J}{\partial t} + \frac{\partial J}{\partial x} = -B(t,x)\, J(t,x),\tag{13}\\ &J(t,0)=\int_0^\infty A(t,x)\, J(t,x)\, dx, \end{align} la reproductivité d'un type peut se définir comme le nombre réel positif T tel que le système (13) avec la condition au bord \[ J(t,0)=\int_0^\infty \Bigl (\frac{P A(t,x)}{T} + (\mathcal{I}-P) A(t,x)\Bigr ) J(t,x)\, dx\] ait un paramètre malthusien nul (Thieme, 1984), ou de manière équivalente, une reproductivité (Bacaër et Guernaoui, 2006 ; Bacaër et Ait Dads, 2011) égale à 1, pourvu que le système (13) avec la condition au bord \[ J(t,0)=\int_0^\infty (\mathcal{I}-P)\,A(t,x) \, J(t,x)\, dx,\] ait un paramètre malthusien négatif (ou une reproductivité < 1). On voit facilement que cette définition coïncide avec (12) si \(\,A(t,x)\) et \(B(t,x)\,\) ne dépendent pas de x.

5.3   Application

    Comme exemple, considérons le modèle de la section 4. Le nombre de rats dans l'état sans maladie est \(S^*=K(r/m-1)\). On définit

•  \(T_R\) : la reproductivité associée aux rats
•  \(T_F\) : la reproductivité associée aux puces
•  \(\,J(t)\) : le vecteur colonne \((I(t), F(t))\,\).

    Il faut noter qu'un calcul similaire a été fait pour des maladies à vecteurs dans (Bacaër, 2007). Ce qui était appelé reproductivité était en réalité la reproductivité d'un type (\(T\) était appelé  \(R_0\) et \(R_0\) était appelé  \(r_0\)). Dans le cas particulier des systèmes périodiques 2×2 tels que (14)-(15), (Bacaër, 2007) a déjà montré que \((R_0)^2=T_R=T_F\,\), comme dans le cas autonome (Roberts et Heesterbeek, 2003).

6.   Dynamique lente-rapide et le modèle SIR

    Dans la section 4, on a remarqué que la courbe pour le nombre de décès dus à la peste n'était pas sensible au changement du paramètre c. L'explication est simple: le temps moyen nécessaire aux puces pour trouver un nouvel hôte, \(\,1/c=1\,\) jour ou 1/30 de mois, est l'échelle de temps la plus courte dans le modèle (7)-(10). Par conséquent, on peut s'attendre à ce que l'équation (9) soit dans l'état quasi-stationnaire: \(\,c\, F\simeq f\, \pi' (1-\varepsilon-\varepsilon') m'\, I\). On remplace c F dans les équations (7), (8) et (10). On obtient le système réduit suivant, qui ne fait pas intervenir c : \begin{align} &\frac{dS}{dt} = b(P) - m\, S - (1-\omega)\, \pi(\theta)\, \frac{S}{P}\, f\, \pi' (1-\varepsilon-\varepsilon') m'\, I+ \varepsilon\, m'\, I,\tag{16}\\ &\frac{dI}{dt} = (1-\omega)\, \pi(\theta)\, \frac{S}{P}\, f\, \pi' (1-\varepsilon-\varepsilon') m'\, I - m'\, I,\tag{17}\\ & \frac{dR}{dt}=\varepsilon'\, m'\, I - m\, R,\tag{18}\\ & \frac{dH}{dt}= \omega\, \pi(\theta)\, f\, \pi' (1-\varepsilon-\varepsilon') m'\, I - a\, H,\quad \quad D(t) = \sigma\, a \, H(t).\tag{19} \end{align} On peut vérifier que la solution périodique de ce système est effectivement très proche de celle du système (7)-(10) avec c = 30 par mois et même plus proche si c = 60 par mois (figure non montrée). Considérons maintenant l'équation (17). Comme il n'y a qu'un seul type d'hôte obligatoire dans le système réduit, la reproductivité  \(R_0\,\) et la reproductivité d'un type T coïncident et sont égaux à la moyenne temporelle \(\,(1-\omega)\, [\frac{1}{\tau}\int_0^\tau \pi(\theta(t))\, dt]\, f\, \pi' (1-\varepsilon-\varepsilon')\). (Bacaër et Guernaoui, 2006, équation (31)) a donné une telle formule faisant intervenir la moyenne (avec une définition correcte de \(\,R_0\)). Numériquement on obtient T ≈ 1,79. On ne peut pas distinguer biologiquement cette valeur de la valeur 1,78 obtenue dans la section 5 avec la théorie de Floquet.

    Remarquer que (16)-(18) est une sorte de version périodique du modèle SIR (2) de Kermack et McKendrick mais avec démographie et un retour possible après guérison dans la classe saine. Le nombre de décès donné par (19) suit les variations de \(\,I(t)\) avec un retard \(1/a\) d'une semaine.

7.   Conclusion

    Même si l'on a répondu déjà dans la section 3 aux deux questions de l'introduction concernant les valeurs des paramètres et de la reproductivité, il s'est avéré que le modèle proposé par Kermack et McKendrick n'était vraiment pas bon d'un point de vue biologique. Même si l'épidémie de 1906 n'a duré que quelques mois, l'influence de la saisonnalité ne peut être négligée. On a donc proposé un nouveau modèle périodique dans la section 4. Comme le modèle comprenait deux hôtes différents, on a calculé la reproductivité d'un type plutôt que  \(R_0\,\) dans la section 5. On a ainsi étendu la notion de reproductivité d'un type aux modèles saisonniers. Enfin, dans la section 6, on a ajouté quelques remarques reliant la reproductivité d'un type pour le modèle avec deux hôtes et la reproductivité d'un modèle réduit avec un seul hôte.

    De notre point de vue, les problèmes posés par le modèle de Kermack et McKendrick pour l'épidémie de peste à Bombay en 1906, une maladie d'un intérêt limité pour la santé publique de nos jours, n'auraient pas d'importance si ce modèle n'était utilisé dans les manuels comme l'un des meilleurs exemples pour montrer comment un modèle mathématique peut expliquer le processus épidémique et peut s'ajuster aux données. Le premier problème était la taille de la population à risque. De nombreux modèles accordent beaucoup d'attention à l'estimation de la reproductivité, qui dans les modèles simples est étroitement liée à la fraction finale de la population qui finit par être infectée. Mais à quelle population s'appliquent ces calculs? Est-ce la population du quartier où l'épidémie démarre, la population de la ville, de la région ou du pays entier? Il semblerait qu'il y ait beaucoup plus d'incertitude sur N que sur \(\,R_0\). Or les deux sont nécessaires pour prédire la taille finale de l'épidémie; et d'une certaine manière, N est encore plus critique pour avoir l'ordre de grandeur de l'épidémie.

    Le second problème était que le modèle de Kermack et McKendrick ne tenait pas compte de la saisonnalité, même si c'est l'une des caractéristiques les plus évidentes de la figure 2. Cette remarque peut également se revéler pertinente pour certaines études contemporaines sur la grippe.

    La saisonnalité des épidémies de peste fait l'objet d'une attention renouvelée ces dernières années suite à la controverse au sujet de l'implication éventuelle du bacille Yersinia pestis lors de la peste noire du 14e siècle. La saisonnalité des épidémies de peste du début du 20e siècle en Inde et son interpretation en terme de seuil de température ont semblé contredire les données européennes du 14e au 18e siècle (Cohn, 2002 et 2010 ; Welford et Bossak, 2009). À l'avenir, il faudrait peut-être essayer d'expliquer par des modèles mathématiques ces différences de saisonnalité.

Remerciements

    Cet article a été stimulé par les questions de Yann Dartois, du lycée Alfred Kastler à Pontoise, par la présentation de Mick Roberts sur la reproductivité d'un type à la conférence CMPD3 (Bordeaux, juin 2010), par une discussion avec Hans Metz, et par le professeur Klaus Dietz qui a envoyé une copie de (Dietz, 2009).

Références bibliographiques