Sur les processus linéaires de naissance et de mort dans un environnement aléatoire

Résumé

On étudie la probabilité d'extinction pour des processus linéaires de naissance et de mort à un ou plusieurs types dans un environnement évoluant suivant une chaîne de Markov. La probabilité d'extinction est presque sûrement égale à 1 si et seulement si la reproductivité est inférieure ou égale à 1. Le point clé est de trouver la définition convenable de la reproductivité pour que ce résultat soit vrai.

1.   Introduction

    Un article récent de Bacaër et Ait Dads (2012) étudie la probabilité d'extinction ω pour un processus linéaire de naissance et de mort avec plusieurs types dans un environnement périodique. Dans ce cas ω=1 si la reproductivité \(\,R_0\,\) (Dublin et Lotka, 1925) est inférieure ou égale à 1, tandis que ω < 1 si \(R_0 > 1\). L'emploi de la reproductivité est motivé par des applications en épidémiologie. La preuve utilise la technique standard basée sur l'équation aux dérivées partielles linéaire du premier ordre satisfaite par une fonction génératrice (Kendall, 1948). Pour les modèles périodiques de période T à un seul type, avec un taux de naissance \(a(t)\) et avec une mortalité \(b(t)\,\), \[R_0=\frac{\int_0^T a(t)\, dt}{\int_0^T b(t)\, dt}.\] La même reproductivité sert aussi de seuil pour les modèles de population périodiques sans stochasticité démographique (Bacaër et Guernaoui, 2006, Sect. 5).

    L'objectif ici est d'étudier les processus linéaires de naissance et de mort à plusieurs types dans un environnement aléatoire. Essayons de résumer la littérature sur ce sujet. Pour des modèles de population en temps discret dans un environnement aléatoire mais sans stochasticité démographique, l'espérance de la population peut croître à l'infini même si l'extinction se produit presque sûrement (Lewontin et Cohen, 1969). Voir aussi (Haccou et coll., 2005). Athreya et Karlin (1971) ont étudié les processus de branchement en temps discret dans un environnement aléatoire, à la fois dans le cas d'un seul type et celui de plusieurs types. Cogburn et Torrez (1981) ont étudié les processus linéaires de naissance et de mort à un seul type dans un environnement aléatoire. S'il y a un nombre fini d'environnements,

• \(a_k\,\) est le taux de naissance
• \(b_k\,\) est la mortalité
• \(u_k\,\) est la proportion moyenne du temps passée dans l'environnement k.

    Britton et Lindholm (2009) ont étudié le même processus, avec un seul type d'individu, dans le cas particulier de deux environnements. Ils ont suggéré que ω=1 si et seulement si \(\,R_\star\leq 1\,\), avec \[R_\star=m_1 m_2, \quad m_k=\int_0^\infty q_k\, e^{-q_k\tau} e^{(a_k-b_k)\tau}\, d\tau.\] \(q_k\,\) est la taux auquel l'environnement quitte l'état k. Ils ont aussi montré que \(\,R_\star\) avait la même position par rapport à 1 que le rayon spectral de la « matrice de prochaine génération » \begin{equation}\tag{2} \left (\begin{array}{cc} a_1 & 0\\ 0 & a_2 \end{array}\right ) \left (\begin{array}{cc} b_1+q_1 & -q_2\\ -q_1 & b_2+q_2 \end{array}\right )^{-1}. \end{equation} Ils ont appelé le rayon spectral de cette matrice \(\,R_0\).

    (Gray et coll., 2012) ont étudié un modèle de population en temps continu et environnement aléatoire mais sans stochasticité démographique. Ils ont remarqué que la position de \begin{equation}\tag{3} \frac{\sum_k a_k \, u_k}{\sum_k b_k\, u_k} \end{equation} par rapport à 1 sert de seuil pour l'extinction. Ils ont nommé ce nombre \(\,T_0\). Ils ont gardé la notation \(\,R_0\,\) pour le rayon spectral de (2). Remarquer que le seuil donné par (3) est le même que (1).

    Bacaër et Khaladi (2012) ont montré que (3) était le rayon spectral d'un opérateur « de prochaine géneration » en dimension infinie et ont suggéré de garder la notation \(\,R_0\,\). (Hernandez-Suarez et coll., 2012) et (Artalejo et coll., 2012) ont également abordé des problèmes reliés concernant la reproductivité. Comme on le verra ci-dessous, à part le problème des notations, (3) et \(\,R_\star\,\) (ou le rayon spectral de (2)) peuvent ne pas avoir la même position par rapport à 1.

    Dans la section 2, on présente deux preuves alternatives du résultat de Cogburn et Torrez (1981) pour les modèles à un seul type. La première preuve utilise une formule de Kendall (1948) pour la probabilité d'extinction dans un environnement variable. La seconde preuve ramène le problème en temps continu au cadre en temps discret d'Athreya et Karlin (1971). On discute aussi en détail un exemple simple avec juste deux environnements, qui espérons-le clarifiera les problèmes concernant la définition de la reproductivit&é mentionnés ci-dessus. La section 3 étudie la probabilité d'extinction pour des populations de plusieurs types dans un cadre avec temps continu. On réduit une nouvelle fois le problème au cas en temps discret d'Athreya et Karlin (1971). Ceci ne semble possible que pour un nombre fini d'environnements. Il se peut que l'approche suivant Kendall (1948) puisse aussi être généralisée au cas de plusieurs types en utilisant les résultats de (Chueshov, 2002) ou de (Benaïm et Schreiber, 2009), éventuellement sans la restriction d'un nombre fini d'environnements. On présente aussi des simulations numériques. La conclusion suggère d'autres possibilités de généralisation.

2.   Le modèle à un seul type

2.1   La probabilité d'extinction

    Soit un processus linéaire de naissance et de mort à un seul type dans un environnement variable. \(a(t)\,\) est le taux de naissance et \(b(t)\) la mortalité au temps t. On suppose \(a(t)=a_{\theta(t)}\) et \(b(t)=b_{\theta(t)}\). \(\,\theta(t)\) est un processus stochastique à valeurs dans \(\{1,2,\ldots,K\}\), qui représentent différents environnements. On suppose \(a_k > 0\) et \(b_k > 0\,\) pour tout k. On suppose que les basculements entre les environnements suivent une chaîne de Markov homogène en temps continu. \(Q_{k,\ell}\geq 0\,\) est le taux auquel l'environnement bascule de \(\ell\,\) vers k (\(k\neq \ell\)). Q est la matrice correspondante avec \[Q_{\ell,\ell}=-q_\ell,\quad q_\ell=\sum_{k\neq \ell} Q_{k,\ell}.\] On suppose que la matrice Q est irréductible. On a donc \(\,q_k > 0\,\) pour tout k. Par conséquent, il existe une unique distribution de probabilités stationnaire et strictement positive u avec \[Qu=0,\quad \sum_k u_k=1, \quad u_k > 0\quad \forall \, k\] (Pardoux, 2008, p. 147). \(R_0\,\) est donné par la formule (3). Soit ω la probabilité d'extinction partant d'un individu au temps 0 dans l'environnement \(\,k_0\). La proposition suivante, bien qu'un cas spécial des résultats de Cogburn et Torrez (1981), sera démontrée d'une manière un peu plus simple et de deux façons différentes.

    Proposition 1.

• ω=1 presque sûrement si \(\,R_0\leq 1\),
• ω < 1 presque sûrement si \(\,R_0 > 1\).

    Preuve. On sait d'après (Kendall, 1948, équation (18)) que \begin{equation}\tag{4} \omega=1-\frac{1}{1+\int_{0}^\infty b(s)\, \exp \bigl [\int_{0}^s (b(v)-a(v))\, dv\bigr ]\, ds}\, , \end{equation} que l'intégrale au dénominateur soit finie ou infinie. D'après le théorème ergodique (Pardoux, 2008, p. 150), \[\lim_{s\to +\infty} \frac{1}{s} \int_{0}^s (b(v)-a(v))\, dv = \sum_k (b_k-a_k)\, u_k \] presque sûrement. Dans le cas \(\,R_0 < 1\,\), on a \(\,\sum_k (b_k-a_k)\, u_k > 0\,\) et l'intégrale au dénominateur de (4) diverge. On a donc ω=1. Dans le cas \(\,R_0 > 1\,\), on a \(\,\sum_k (b_k-a_k)\, u_k < 0\,\) et l'intégrale au dénominateur de (4) converge. On a donc ω < 1.

    On n'a pas considéré le cas critique \(R_0=1\). Cependant, voici une seconde preuve de la proposition 1, qui couvre aussi le cas critique.

    Preuve. Le processus en temps continu à K états est lié à une chaîne de Markov en temps discret, dont l'espace d'états est \[\mathcal{X}=\{1,2,\ldots,K\}\times \mathbb{R}_+.\] Chaque pas de temps correspond au temps entre deux basculements de l'environnement. Au lieu de dire par exemple que l'environnement est dans l'état k pendant t unités de temps puis dans l'état \(k'\) pendant \(t'\) unités de temps (avec \(k'\neq k\)), on dit qu'il y a la transition suivante \[(k,t)\in \mathcal{X}\longrightarrow (k',t')\in \mathcal{X}.\] La probabilité pour que l'environnement \(\,k'\,\) suive l'environnement k est donnée par \[\Pi_{k',k}=\left \{\begin{array}{lll} \frac{Q_{k',k}}{q_k},& &k'\neq k,\\ 0, & &k'= k. \end{array}\right.\] L'environnement \(k'\) dure entre \(t'\) et \(t'+dt'\) unités de temps (\(dt'\) infiniment petit) avec une probabilité \(q_{k'}\, e^{-q_{k'}t'}\, dt'\). La probabilité pour que l'environnement \(\,k'\,\) dure entre \(t'\) et \(t'+dt'\,\) unités de temps et suive l'environnement k qui a duré t unités de temps, est \[P_{(k,t)\to(k',t')}\, dt' = \Pi_{k',k} \ q_{k'}\, e^{-q_{k'}t'}\, dt'\, .\] On a \[\int_0^\infty \sum_{k'} P_{(k,t)\to(k',t')} dt'=1\, .\] Plus généralement, pour \(z\in \{1,2,\ldots\}\,\), la probabilité de transition en z étapes est donnée par \[P^{(z)}_{(k,t)\to(k',t')}\, dt' = (\Pi^z)_{k',k} \ q_{k'}\, e^{-q_{k'}t'}\, dt'\, .\] \(\Pi^z\) est la produit itéré de la matrice \(\Pi=(\Pi_{k',k})\). \(Qu=0\) est équivalent à \[\sum_{k\neq k'} Q_{k',k} u_k=q_{k'} u_{k'},\quad \forall k'.\] Avec \begin{equation}\tag{5} w_{k,t}=\frac{q_k u_k}{\sum_\ell q_\ell u_\ell}\, q_k\, e^{-q_k t} \end{equation} on a donc \[ \sum_k \int_0^\infty w_{k,t}\, dt =1,\quad \quad \sum_k \int_0^\infty w_{k,t}\, P_{(k,t)\to(k',t')} \, dt = w_{k',t'},\quad \forall (k',t')\in \mathcal{X}.\] \((w_{k,t})\) est donc une distribution de probabilités stationnaire et la chaîne de Markov dans \(\,\mathcal{X}\,\) est récurrente positive (Meyn et Tweedie, 1993). Athreya et Karlin (1971) mentionnent dans une remarque suivant leur théorème 4 que leurs résultats restent valables non seulement pour les chaînes de Markov irréductibles récurrentes positives sur un espace d'états dénombrable mais aussi pour un processus stationnaire ergodique sur un espace d'états général (non dénombrable) tel que \(\,\mathcal{X}\).

    Entre les basculements de l'environnement, on a un processus linéaire de naissance et de mort dans un environnement constant. Dans un environnement k durant t unités de temps, soit \(\,\phi_{k,t}(x)\) la fonction génératrice de la population au bout de l'intervalle de temps, partant d'un individu au début de cet intervalle de temps: \[\phi_{k,t}(x)=\frac{b_k(1-x) e^{t(a_k-b_k)} + a_k x-b_k}{a_k(1-x) e^{t(a_k-b_k)}+a_k x-b_k}\] si \(a_k\neq b_k\) tandis que \[\phi_{k,t}(x)=\frac{x+(1-x)a_k t}{1+(1-x) a_k t}\] si \(a_k=b_k\,\) (Hillion, 1986, p. 118). L'espérance de la population au bout de l'intervalle de temps est égale à \[\phi_{k,t}'(1)=e^{(a_k-b_k)t}.\] La probabilité que la population soit éteinte au bout de l'intervalle de temps est \[\phi_{k,t}(0)=\frac{1-e^{(a_k-b_k)t}}{1-e^{(a_k-b_k)t}\, a_k/b_k}\, \] si \(a_k\neq b_k\,\), tandis que \(\phi_{k,t}(0)=a_k\, t/(1+a_k\, t)\) si \(a_k=b_k\). Avec \(\,a_k < b_k\,\), on a \[1-\phi_{k,t}(0)\sim_{t\to +\infty} (1-a_k/b_k)\, e^{(a_k-b_k)t}.\] Avec \(a_k=b_k\,\), on a \[1-\phi_{k,t}(0)\sim_{t\to +\infty} 1/(a_k\, t).\] Donc on peut facilement vérifier que \begin{align*} &\mathbb{E}(|\log (1-\phi(0))|)=\sum_k \int_0^\infty w_{k,t} | \log (1- \phi_{k,t}(0)) | \, dt < +\infty\, ,\\ &\mathbb{E}([\log \phi'(1)]^+)=\sum_k \int_0^\infty w_{k,t} [ \log \phi_{k,t}'(1)]^+ \, dt < +\infty\, , \end{align*} à cause de la décroissance exponentielle de \(w_{k,t}\,\) par rapport à t. Avec (Athreya et Karlin, 1971), on conclut que ω=1 si et seulement si \[ \mathbb{E}(\log \phi'(1)) = \sum_k \int_0^\infty w_{k,t} \log \phi'_{k,t}(1)\, dt \leq 0.\] Avec \(\int_0^\infty t\, e^{-q_kt}\, dt = 1/(q_k)^2\), on obtient \[\mathbb{E}(\log \phi'(1)) = \sum_k \int_0^\infty \frac{q_k u_k}{\sum_\ell q_\ell u_\ell}\, q_k\, e^{-q_k t} [(a_k-b_k)t]\, dt=\frac{\sum_k (a_k-b_k)u_k}{\sum_\ell q_\ell u_\ell}\, .\] Donc ω=1 si et seulement si \(R_0\leq 1\).

2.2   Un exemple et quelques remarques

    Comme dans l'exemple de Britton et Lindholm (2009, section 3), on suppose qu'il y a deux environnements:

• \(a_1= \mbox{2,7}\) et \(b_1=2\)
• \(a_2=\mbox{0,8}\) et \(b_2=2\).

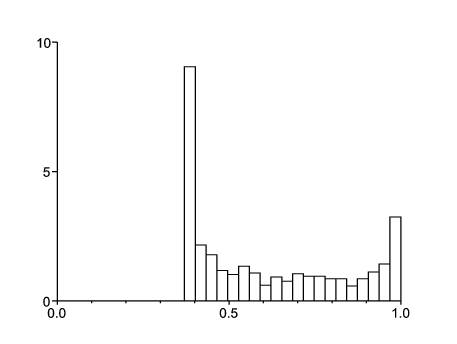
    Comme autre exemple, considérons les mêmes valeurs des paramètres sauf que \(a_1\) est doublé: \(a_1=\mbox{5,4}\). Dans ce cas on a \(R_0= \mbox{1,55} > 1\). La figure 1b montre un histogramme de la probabilité d'extinction ω en partant d'une personne dans l'environnement 1. La moyenne de la probabilité d'extinction est environ 0,61. Cette moyenne serait 0,85 en partant de l'environnement 2. L'histogramme a été obtenu en approchant la chaîne de Markov en temps continu, qui gouverne l'environnement \(\,(0 < t < 100)\,\), par une chaîne de Markov en temps discret avec un pas de temps \(\,\varepsilon=0,00005\). L'ordinateur choisit aléatoirement 1000 réalisations de cette chaîne de Markov, formant 1000 histoires environnementales. La formule (4) pour ω est ensuite estimée numériquement. Avec \(\,b_1=b_2\), \(a_2\leq a_1\) et \(a_1\geq b_1\,\), on s'aperçoit facilement avec (4) que \(\omega \geq b_1/a_1\). Cette borne inférieure correspond à la probabilité d'extinction si l'environnement est toujours 1. Avec les valeurs numériques ci-dessus, on obtient \(\omega\geq 2/ \mbox{5,4} \simeq \mbox{0,37}\,\), en accord avec la figure 1b.

    Sous-criticalité du modèle discrétisé. Pour dessiner la figure 1, on a discrétisé le processus en temps continu en utilisant un pas de temps ε>0. Pour simplifier, supposons comme dans l'exemple qu'il n'y ait que K=2 environnements. La matrice de transition de la chaîne de Markov en temps discret est \[\mathcal{P}=\left (\begin{array}{cc} 1-q_1\varepsilon & q_2\varepsilon \\ q_1\varepsilon & 1-q_2\varepsilon \end{array}\right ).\] Sa distribution stationnaire \(\varpi\) est telle que \(\mathcal{P}\varpi=\varpi\) avec \(\sum\varpi_k=1\). On obtient \(\,\varpi_1=q_2/(q_1+q_2)\) et \(\varpi_2=q_1/(q_1+q_2)\), qui sont indépendants de ε et coïncident avec les distributions stationnaires \(u_1\) et \(u_2\,\) du processus en temps continu. Si l'environnement est de type k (\(k=1\) ou 2), on a supposé que pendant un pas de temps chaque individu a une probabilité de donner naissance \(a_k\varepsilon\) et une probabilité de mourir \(b_k\varepsilon\). Au pas de temps suivant, chaque individu conduit

• à aucun individu avec une probabilité \((1-a_k\varepsilon)b_k\varepsilon\) [pas de naissance, une mort],
• à 1 individu avec une probabilité \((1-a_k\varepsilon)(1-b_k\varepsilon)+a_k\varepsilon b_k\varepsilon\) [soit pas de naissance et pas de mort, soit une naissance et une mort],
• à 2 individus avec une probabilité \(a_k\varepsilon (1-b_k\varepsilon)\) [une naissance, pas de mort].

    Une autre manière d'utiliser les résultats d'Athreya et Karlin. Une autre manière de voir cet exemple avec seulement deux environnements est de le considérer comme un processus de branchement dans une suite « d'environnements » aléatoires indépendants et identiquement distribués. En effet la séquence d'environnements \(\,1\to 2\,\) se répète à l'identique, le temps passé dans chaque environnement étant aléatoire. La probabilité pour que l'environnement k (\(k=1\) ou 2) dure entre \(t_k\) et \(t_k+dt_k\) unités de temps est \(q_k\, e^{-q_k t_k}\, dt_k\). Ces probabilités sont indépendantes. Le nouvel espace des « environnements » est donc \(\{(t_1,t_2)\in (\mathbb{R}_+)^2\}\). Si chaque environnement dure \(\,t_k\) unités de temps, alors la croissance moyenne durant une séquence est \[\mathcal{M}=e^{(a_1-b_1)t_1} e^{(a_2-b_2)t_2}.\] La théorie des processus de branchement dans les environnements indépendants et identiquement distribués (Athreya et Karlin, 1971) montre que \(\,\omega=1\) si et seulement si \[\mathbb{E}(\log \mathcal{M}) = \int_0^\infty \!\!\int_0^\infty q_1\, e^{-q_1 t_1} q_2\, e^{-q_2 t_2} \log \left ( e^{(a_1-b_1)t_1} e^{(a_2-b_2)t_2} \right ) dt_1\, dt_2 \leq 0.\] Mais on voit que \begin{align*} \mathbb{E}(\log \mathcal{M}) &= \int_0^\infty \!\!\int_0^\infty q_1\, e^{-q_1 t_1} q_2\, e^{-q_2 t_2} \bigl [(a_1-b_1)t_1+(a_2-b_2)t_2 \bigr ] dt_1\, dt_2\\ &= \int_0^\infty q_1\, e^{-q_1 t_1} (a_1-b_1)t_1\, dt_1 + \int_0^\infty q_2\, e^{-q_2 t_2} (a_2-b_2)t_2\, dt_2. \end{align*} On a donc \[ \mathbb{E}(\log \mathcal{M}) =\frac{(a_1-b_1)q_2+(a_2-b_2)q_1}{q_1 q_2}\, .\] Le signe de cette quantité est le même que celui de \(R_0-1\). Il y a extinction presque sûrement si et seulement si \(\,R_0\leq 1\).

    Une autre manière de calculer la probabilité d'extinction. \(\,p_{k,n}(t)\,\) est la probabilité que la population soit dans l'environnement k au temps t avec n individus. Le processus est considéré comme une chaîne de Markov homogène en temps continu. L'espace d'états est \(\,\{1,2,\ldots,K\}\times \mathbb{N}\). Comme dans l'équation (2) de (Yechiali, 1973), on obtient \begin{align} \frac{dp_{k,n}}{dt} =& -(a_k+b_k)n \,p_{k,n} + b_k (n+1) p_{k,n+1} + a_k (n-1) p_{k,n-1} \nonumber\\ &+ \sum_{\ell\neq k} \left (Q_{k,\ell} p_{\ell,n} - Q_{\ell,k} p_{k,n} \right )\, . \tag{6} \end{align} Considérons la chaîne de Markov induite en temps discret, obtenue en ne considérant que les sauts du processus en temps continu :

• \(a_k n /(a_k n + b_k n +q_k)\) est la probabilité de la transition \((k,n) \to (k,n+1)\),
• \(b_k n /(a_k n + b_k n +q_k)\) est la probabilité de la transition \((k,n) \to (k,n-1)\)
• \(Q_{\ell,k} /(a_k n + b_k n +q_k)\) est la probabilité de la transition \((k,n) \to (\ell,n)\) si \(\ell\neq k\).

• \(\pi_{k,n}(j)\,\) la probabilité que le système soit après j transitions dans la position \((k,n)\)
• \(\pi(j)=(\pi_{k,n}(j))\) le vecteur formé de ces probabilités, avec les indices \((k,n)\) rangés comme ci-dessus
• \(\delta_{k,\ell}=1\) si \(k=\ell\) et \(\delta_{k,\ell}=0\) si \(k\neq \ell\). \(\delta_{k,\ell}\) est le symbole de Kronecker.

2.3   Lien avec l'espérance de la population

    Une autre manière de voir cela est de considérer la suite d'environnements \[1\to 2\to 1\to 2\cdots\] \(\,\tau_n^{(k)}\,\) est la durée aléatoire passée dans l'environnement k (k=1 ou 2) lors du cycle n (n≥1). En d'autres termes, l'environnement est

• dans l'état 1 pendant \(\tau_1^{(1)}\) unités de temps,
• puis dans l'état 2 pendant \(\tau_1^{(2)}\) unités de temps,
• puis dans l'état 1 pendant \(\tau_2^{(1)}\) unités de temps, etc.

    Noter cependant que ces remarques ne sont pas directement liées à la proposition 1 car elle donne des informations sur l'espérance de la population et non sur la probabilité que cette population s'éteigne. En réalité, pour des processus de branchement en temps discret dans un environnement aléatoire, la population peut très bien être sous-critique et tendre vers l'extinction presque sûrement, même si l'espérance de la population converge vers l'infini (Haccou et coll., 2005, p. 51).

2.4   Autres remarques

    Un autre paramètre lié à la croissance d'une espérance mathématique.

    (Gray et coll., 2012) ont montré que la position de (3) par rapport à 1 sert de seuil entre l'extinction et la persistance pour un modèle épidémique de type SIS constitué d'équations différentielles dans un environnement aléatoire. Il n'y a pas de stochasticité démographique. Gray et coll. (2012) utilisent pour (3) la notation \(\,T_0\). Britton et Lindholm (2009) utilisent la notation \(\tilde{R}_0\,\).

    Ces deux références utilisent la notation \(\,R_0\,\) pour un nombre différent, à savoir le rayon spectral de (2) dans le cas de deux environnements. Nommons-le \(R^*\,\) pour éviter la confusion. Dans le cas des modèles en temps discret, (Bacaër et Khaladi, 2012) nomme ce nombre \(\,R_*\). Comme expliqué ci-dessous, la position de ce nombre par rapport à 1 décide si une certaine espérance croît ou décroît. \(R^*\,\) s'obtient en général de la manière suivante. Pour un calcul informel dans le cas particulier K=2, voir la section 3 de (Gray et coll., 2012). Considérons une fois encore la chaîne de Markov (6) en temps continu sur l'espace d'états \(\{1,2,\ldots,K\}\times \mathbb{N}\). On définit \[E_k(t)=\sum_{n\geq 1} n\, p_{k,n}(t).\] Alors on voit facilement que \[\frac{dE_k}{dt} = (a_k-b_k) E_k + \sum_{\ell\neq k} \left (Q_{k,\ell} E_{\ell} - Q_{\ell,k} E_{k} \right )\, .\] On définit \[A=\mathrm{diag}(a_1,\ldots,a_K),\quad B=\mathrm{diag}(b_1,\ldots,b_K)\] et \(E(t)=(E_1(t),\ldots,E_K(t))\), le vecteur des espérances. On a alors \[\frac{dE}{dt} = (A-B+Q)E.\] D'après (Diekmann et coll., 2013), le vecteur des espérances converge vers l'infini si et seulement si le rayon spectral \(R^*\) de \(A(B-Q)^{-1}\) est strictement supérieur à 1. Pour l'exemple numérique ci-dessus avec \(a_1= \mbox{2,7}\), on obtient \[R^*=\rho(A(B-Q)^{-1})=\rho \left ( \begin{array}{cc} \frac{a_1(b_2+q_2)}{b_1b_2+q_1b_2+q_2b_1} & \frac{a_1 q_2}{b_1b_2+q_1b_2+q_2b_1} \\ \frac{a_2 q_1}{b_1b_2+q_1b_2+q_2b_1} & \frac{a_2(b_1+q_1)}{b_1b_2+q_1b_2+q_2b_1} \end{array}\right ) \simeq \mbox{1,057} > 1.\] Rappelons dans ce cas que \(R_0= \mbox{0,875} < 1\,\) et ω=1. Donc la position de \(\,R^*\) par rapport à 1 décide de la croissance de l'espérance mais ne donne pas le bon seuil pour l'extinction.

    Encore un autre paramètre. Comme déjà noté ci-dessus, la suite des environnements est périodique quand il n'y a que deux environnements possibles: \(\,1\to 2\to 1\to 2\cdots\). Si l'environnement est k, alors l'espérance de la population engendrée par un seul individu est \(\,e^{(a_k-b_k)t}\) après t unités de temps. L'environnement k dure entre t et \(\,t+dt\) unités de temps avec une probabilité \(q_k\, e^{-q_k t} dt\). Donc l'espérance de la population engendrée par un individu dans l'environnement k est \begin{equation} m_k=\int_0^\infty q_k\, e^{-q_k t} e^{(a_k-b_k)t} dt = \frac{q_k}{b_k+q_k-a_k} = \frac{1}{1-\frac{a_k-b_k}{q_k}}, \quad k\in \{1,2\} \end{equation} pourvu que \(b_k+q_k > a_k\). Cette condition est vérifiée si \(\,a_1=\mbox{2,7}\). On a \(\,b_1+q_1-a_1= \mbox{0,3}\) et \(b_2+q_2-a_2= \mbox{2,2}\). Noter que \(m_k=+\infty\) lorsque \(b_k+q_k\leq a_k\). On définit \(\,R_\star=m_1 m_2\) (à ne pas confondre avec le \(R^*\,\) de la précédente remarque). On a alors \(\,R_\star=1/ \mbox{0,66} \simeq \mbox{1,52} > 1\). Britton et Lindholm (2009, Section 3) ont suggéré que \(\,R_\star > 1\) était équivalent à \(\omega < 1\). Mais ici on a \(R_\star > 1\) tandis que \(\omega=1\). Donc on voit que la position de \(\,R_\star\,\) par rapport à 1 ne donne pas le bon seuil pour l'extinction. Si K=2, le §5.1 de Britton et Lindholm (2009) montre (avec nos notations) que \(R_\star > 1\) si et seulement si \(R^* > 1\).

3.   Les modèles à plusieurs types

    On étudie les processus linéaires de naissance et de mort &avec plusieurs types d'individus dans un environnement variable dans le temps. \(p(t,n_1,\ldots,n_m)\) est la probabilité d'avoir \(n_i\,\) personnes de type i au temps t (\(1\leq i\leq m\)). La fonction génératrice \[g(t,x_1,\ldots,x_m)=\sum_{n_1,\ldots,n_m\geq 0} p(t,n_1,\ldots,n_m)\ x_1^{n_1}\ldots x_m^{n_m}\] est solution de l'équation \begin{equation}\tag{7} \frac{\partial g}{\partial t}=\sum_{i,j} \bigl [A_{i,j}(t) x_j - B_{i,j}(t)](x_i-1) \, \frac{\partial g}{\partial x_j} \end{equation} (Bacaër et Ait Dads, 2012). La matrice des naissances \(A(t)=(A_{i,j}(t))_{1\leq i,j\leq m}\,\) est à coefficients positifs ou nuls. La matrice des mortalités \(B(t)=(B_{i,j}(t))\) est de la forme \begin{equation} B_{i,j}(t)=-b_{i,j}(t)\quad \forall i\neq j,\quad B_{j,j}(t)=b_{j,j}(t)+\sum_{i\neq j} b_{i,j}(t)\quad \forall j,\quad b_{i,j}(t)\geq 0 \quad \forall i,j. \end{equation} On suppose que les matrices \((A(t),B(t))\) appartiennent à une liste finie d'environnements \(((A^{(k)},B^{(k)}))_{1\leq k\leq K}\), c'est-à-dire \(A(t)=A^{(\theta(t))}\) et \(B(t)=B^{(\theta(t))}\) avec \(\theta(t)\) un processus stochastique à valeurs dans \(\{1,2,\ldots,K\}\). On suppose encore une fois que les transitions entre les environnements suivent une chaîne de Markov homogène en temps continu. \(Q_{k,\ell}\) est le taux auquel l'environnement peut basculer de (\(\ell\to k\), \(k\neq \ell\)). Soit Q la matrice de transition correspondante avec \[Q_{\ell,\ell}=-q_\ell,\quad q_\ell=\sum_{k\neq \ell} Q_{k,\ell}.\] On suppose que la matrice Q soit irréductible. Par conséquent, il y a une unique distribution stationnaire u telle que \(\,Qu=0\) et \(\sum_k u_k=1\). Enfin on suppose que \(b_{j,j}^{(k)} > 0\,\) pour tout k et j. Cette hypothèse implique que le plus grand exposant de Lyapunov du système différentiel aléatoire \(\,dZ/dt = -B(t) Z(t)\) est strictement négatif.

    Au temps t=0, on suppose que

• il y a \(\nu_i\,\) personnes de type i, avec \(\nu_i\in \mathbb{N}\)
• \(\exists\, i,\ \nu_i > 0\).

    Comme l'expliquent par exemple Bacaër et Ait Dads (2012), ω peut être calculé en utilisant les courbes caractéristiques de (7). Avec \(\,\tau\geq 0\,\), \(Y^{(\tau)}\) est la solution unique du système \begin{equation}\tag{8} \frac{dY_j^{(\tau)}}{ds}(s) = \sum_i \left [A_{i,j}(-s)\, \left (1-Y^{(\tau)}_j(s)\right ) - B_{i,j}(-s) \right ] Y^{(\tau)}_i(s) \end{equation} avec la condition initiale \[Y_j^{(\tau)}(-\tau)=1\quad \forall \, j.\] On a alors \[\omega= (\omega_1)^{\nu_1} \cdots (\omega_m)^{\nu_m},\quad \quad \omega_j=1-\lim_{\tau \to +\infty} Y_j^{(\tau)}(0)\, .\] La question est de savoir si \(\omega=1\) ou \(\omega < 1\). Le résultat dépend de la stabilité du système suivant d'équations différentielles aléatoires (Arnold, 1998, Sect. 2.2) \begin{equation}\tag{9} \frac{dX}{dt}=(A(t)-B(t))X(t). \end{equation} C'est l'équation satisfaite par le vecteur des espérances des populations au temps t. Cette stabilité dépend du signe du plus grand exposant de Lyapunov de (9) \[\lambda_1(A,B);\] En suivant Bacaër et Khaladi (2012), la stabilité peut alternativement être formulée en termes de reproductivité \(\,R_0\), qui est l'unique solution de \begin{equation} \lambda_1(A/R_0,B)=0. \end{equation}

    Une manière d'étudier la probabilité d'extinction ω serait d'adapter la méthode utilisée par Bacaër et Ait Dads (2012) pour des environnements périodiques au cas des environnements aléatoires. On prendrait avantage du fait que le système (8) est coopératif et sous-homogène comme dans les travaux de (Chueshov, 2002) ou (Benaïm et Schreiber, 2009). Ceci conduirait à des difficultés techniques telles que le lien entre le plus grand exposant de Lyapunov de (9) et le plus grand exposant de Lyapunov de la linéarisation près de zéro de (8), qui est le système transposé de (9). Voir (Arnold et Wihstutz, 1986) ou (Barreira et Valls, 2008). La preuve de la persistance de (8) quand \(\,R_0 > 1\,\) peut aussi être difficile. Pour éviter ces difficultés, on va utiliser la même idée que dans la seconde preuve de la proposition 1. Pour un nombre fini d'environnements markoviens, le problème en temps continu peut être ramené à un processus de branchement avec plusieurs types, en temps discret, dans un environnement aléatoire. Les résultats d'Athreya et Karlin (1971) peuvent alors être appliqués.

    Proposition 2. On suppose que la matrice suivante est irréductible pour tout k \[C^{(k)}:=A^{(k)}-B^{(k)}.\] On suppose en plus \[ \forall \, k, \exists \, (i,j), \quad A^{(k)}_{i,j} > 0.\]

• On a ω=1 presque sûrement si \({R}_0\leq 1\)
• On a ω<1 presque sûrement si \({R}_0 > 1\) .

    Preuve. On prend \(\,t_0=0\). \((t_n)_{n\geq 1}\) avec \(0 < t_1 < t_2 < \cdots\,\) sont les temps auxquels l'environnement bascule. \(k_n\,\) est l'environnement dans l'intervalle de temps \(]t_n,t_{n+1}[\,\). Dans l'environnement k, un individu de type h au départ engendre une population t unités de temps plus tard dont la fonction génératrice \(\phi^{(k,h)}(t,x_1,\ldots,x_m)\) est solution de \begin{equation}\tag{10} \frac{\partial \phi^{(k,h)}}{\partial t}=\sum_{i,j} \bigl [A^{(k)}_{i,j} x_j - B^{(k)}_{i,j}](x_i-1) \, \frac{\partial \phi^{(k,h)}}{\partial x_j}, \quad \forall t > 0,\ \forall (x_1,\ldots,x_m)\in ]0,1[^m. \end{equation} avec \[\phi^{(k,h)}(0,x_1,\ldots,x_m)=x_h.\] On définit \begin{equation}\tag{11} M_i^{(k,h)}(t)=\frac{\partial \phi^{(k,h)}}{\partial x_i}(t,1,\ldots,1),\quad M^{(k)}(t)=\left (M_i^{(k,h)}(t)\right )_{i,h}. \end{equation} \(M_i^{(k,h)}(t)\) est l'espérance de la population de type i. En partant de (10) ou en se référant à (Athreya et Ney, 1972), on voit (cf. appendice) que \begin{equation}\tag{12} \frac{dM^{(k)}}{dt}(t) = C^{(k)} M^{(k)}(t), \quad \forall t > 0, \end{equation} et \(M^{(k)}(0)=I\,\) (la matrice identité). Par conséquent, \begin{equation} \mathcal{M}_n:=M^{(k_n)}(t_{n+1}-t_n) = \exp\left [C^{(k_n)}(t_{n+1}-t_{n})\right ]\, . \end{equation} Noter avec (9) et (12) que \[\lambda_1(A,B) =\lim_{n\to +\infty} \frac{1}{t_n} \log \| \mathcal{M}_{n-1} \mathcal{M}_{n-2}\cdots \mathcal{M}_0\| \] presque sûrement. D'après Athreya et Karlin (1971, Théorème 12), le signe de cette limite décide s'il y a extinction presque sûrement ou pas. Mais d'abord il faut vérifier les trois hypothèses de ce théorème. L'irréductibilité de \(\,C^{(k_n)}\) implique que tous les coefficients de \(\mathcal{M}_n\) sont strictement positifs (Berman et Plemmons, 1994, Théorème 6.3.12) : la première hypothèse est satisfaite. On définit maintenant \begin{equation}\tag{13} S^{(k,h)}_{i,j}(t)=\frac{\partial^2 \phi^{(k,h)}}{\partial x_i \partial x_j}(t,1,\ldots,1)\ ,\quad S^{(k,h)}(t)=\left (S^{(k,h)}_{i,j}(t)\right )_{i,j} . \end{equation} On peut montrer que tous les coefficients de la matrice \(S^{(k_n,h)}(t_{n+1}-t_n)\,\) sont aussi strictement positifs (cf. appendice): c'est la seconde hypothèse. Enfin on a aussi \[ - \sum_k \int_0^\infty \!\! w_{k,t} \log \left [\sum_{h=1}^m \left ( 1-\phi^{(k,h)}(t,0,\ldots,0) \right ) \right ] dt < +\infty\, ,\] avec \(w_{k,t}\) donné par (5). En effet, d'une part, \(w_{k,t}\) décroît exponentiellement si \(t\to +\infty\). Dautre part, \(1-\phi^{(k,h)}(t,0,\ldots,0)\) ne peut s'approcher de 0 plus vite que \(e^{-ct}\,\) avec c>0. c est donné par le taux auquel la solution de (8) peut s'approcher de 0 dans un environnement k qui est sous-critique. Donc la troisième condition est aussi satisfaite.

    Dans le cas \(R_0\leq 1\), on a \(\lambda_1(A,B)\leq 0\). On conclut que ω=1 presque sûrement grâce à

• (Athreya et Karlin, 1971, Théorème 12(i)) si \(\,\lambda_1(A,B) < 0\)
• (Kaplan, 1974, Théorème 2) si \(\,\lambda_1(A,B)=0\).

    Dans le cas \(R_0 > 1\), on a \(\lambda_1(A,B) > 0\). On conclut que ω<1 avec (Athreya et Karlin, 1971, Théorème 12(ii)).

    Exemple. Comme dans (Bacaër et Ait Dads, 2012), considérons un modèle épidémique SEIR linéarisé, c'est-à-dire un processus de naissance et de mort à deux types. On suppose que l'environnement varie aléatoirement entre deux états. Supposons que la matrice de transition soit constante: \[Q=\left (\begin{array}{cc} -q_1 & q_2\\ q_1 & -q_2 \end{array}\right )\] avec \(q_1 > 0\) et \(q_2 > 0\). La distribution stationnaire est telle que \(\,u_1=q_2/(q_1+q_2)\) et \(u_2=q_1/(q_1+q_2)\). On suppose \[A(t)=\left (\begin{array}{ccc} 0 & &\beta(t)\\ 0 & & 0 \end{array} \right ),\quad B(t)=\left (\begin{array}{cc} \alpha+\mu & 0\\ -\alpha & \gamma+\mu \end{array}\right ), \] avec \(\beta(t)=\beta_1 > 0\) ou \(\beta_2 > 0\) selon l'environnement. \(\alpha > 0\) est le taux auquel les gens infectés mais pas encore infectieux deviennent infectieux, \(\mu > 0\) est la mortalité et \(\gamma > 0\,\) est le taux de guérison. La reproductivité est l'unique nombre positif pour lequel le plus grand exposant de Lyapunov du système suivant est égal à 0 \[\frac{dX}{dt} = (A(t)/R_0-B(t))X(t).\] Noter que si \(\beta(t)\) était constant et égal à sa moyenne temporelle \(u_1\beta_1+u_2\beta_2\), on aurait \(R_0=(u_1\beta_1+u_2\beta_2)\alpha/((\alpha+\mu)(\gamma+\mu))\). Des formules analytiques approchées pour \(\,R_0\) dans un environnement aléatoire peuvent être déduites des formules de (Arnold et Kloeden, 1989) pour le plus grand exposant de Lyapunov des systèmes bidimensionnels.

    La probabilité pour que le processus soit éteint au temps τ>0, en partant de \((E_0,I_0)\) personnes au temps 0, est \[(1-Y_1^{(\tau)}(0))^{E_0} (1-Y_2^{(\tau)}(0))^{I_0},\] avec pour \(-\tau < s < 0\) \begin{align} \frac{dY_1^{(\tau)}}{ds}(s) &= -(\alpha+\mu) Y_1^{(\tau)}(s) + \alpha\, Y_2^{(\tau)}(s),\tag{14}\\ \frac{dY_2^{(\tau)}}{ds}(s) &= \beta(-s)\, Y_1^{(\tau)}(s)\, (1-Y_2^{(\tau)}(s)) -(\gamma+\mu) Y_2^{(\tau)}(s),\tag{15} \end{align} tandis que \(Y_1^{(\tau)}(-\tau)=1\) et \(Y_2^{(\tau)}(-\tau)=1\). Il y a des erreurs de signes dans les équations correspondantes données par Bacaër et Ait Dads (2012) ; les figures 3 et 4 dans cette référence sont néanmoins correctes. \(\omega_1\) et \(\omega_2\) sont les probabilités d'extinction ultimes, en partant soit d'une personne infectée mais non infectieuse, soit d'une personne infectieuse: \[\omega_j=\lim_{\tau\to +\infty} 1-Y_j^{(\tau)}(0),\quad j=1,2.\] La proposition 2 montre \(\omega_1=\omega_2=1\) presque sûrement si \(R_0\leq 1\) et que \(\omega_1 < 1\) et \(\omega_2 < 1\) presque sûrement si \(R_0 > 1\).

    Dans le cas \(\beta_2 \leq \beta_1\,\), un théorème de comparaison pour le système (14)-(15) montre que \(\omega_1\) et \(\omega_2\) sont supérieures aux probabilités correspondantes pour le processus de naissance et de mort où l'environnement est toujours 1. Si ce dernier processus est surcritique alors ces probabilités \(\xi_1\) et \(\xi_2\) se calculent facilement :

• soit on détermine l'état stationnaire de (14)-(15) avec \(\beta(-s)\) remplacé par \(\beta_1\),
• soit on considère le processus de Bienaymé-Galton-Watson induit, avec plusieurs types : \[\xi_1=\frac{\mu}{\alpha+\mu}+\frac{\gamma+\mu}{\beta_1},\quad \xi_2=\frac{\alpha+\mu}{\alpha}\, \frac{\gamma+\mu}{\beta_1}.\]

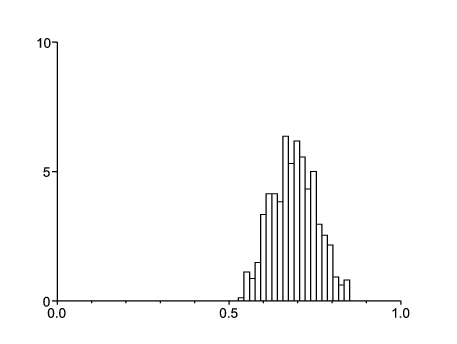
    Prenons \(q_1=q_2=1\), \(\beta_1=2\), \(\beta_2=1\), \(\alpha=1\), \(\mu= \mbox{0,01}\) et \(\gamma=1\). On obtient \(\,R_0\simeq \mbox{1,45} > 1\). Noter que pour le système moyenné en temps, on a \(\,R_0\simeq \mbox{1,47}\). De plus, on obtient \(\xi_1\simeq \xi_2\simeq \mbox{0,51}\). La figure 2 montre l'histogramme pour la probabilité d'extinction partant d'une personne infectée mais non infectieuse dans l'environnement 1. Il a été obtenu avec 1000 simulations de l'histoire environnementale. La moyenne est proche de 0,69 (elle serait 0,66 partant de l'environnement 2). On a pris τ=100 et un pas de temps de 0,001. La figure confirme que \(\omega_1 < 1\) (et \(\omega_2 < 1\)) presque sûrement si \(R_0 > 1\).

4.   Conclusion

    Certaines questions restent ouvertes. On peut se demander, comme Britton et Lindholm (2009), ce qui arrive si la survie n'est pas distribuée exponentiellement, c'est-à-dire pour des processus de Crump-Mode-Jagers tels que dans le travail de (Ball et Donnelly, 1995). Il est aussi clair que la plupart de résultats restent vrais pas seulement pour un nombre fini d'environnements markoviens mais aussi pour des environnements ergodiques plus généraux.

    Pour les applications biologiques, il serait plus réaliste de supposer que la matrice de transition est de la forme \[Q(t)=\left (\begin{array}{cc} -q_1(t) & q_2(t)\\ q_1(t) & -q_2(t) \end{array}\right ),\] où par exemple \(q_1(t)=k_1(1+\varepsilon_1 \cos \omega t)\), \(q_2(t)=k_2(1+\varepsilon_2 \sin \omega t)\), \(k_1 > 0\), \(k_2 > 0\), \(\varepsilon_1\in (0,1)\) et \(\varepsilon_2 \in (0,1)\). De cette manière, l'année est plus ou moins divisée en deux saisons (disons l'été et l'hiver), l'une qui serait favorable à la croissance et l'autre moins favorable. Cela pourrait être le cas pour les maladies infectieuses où le taux effectif de contact dépend de la température. Une matrice périodique \(\,Q(t)\) comme ci-dessus est un modèle de saisonnalité plus réaliste qu'une matrice Q constante. Dans ce dernier cas avec seulement deux environnements, les deux saisons alternent mais les longueurs des saisons sont indépendantes. Pour être réaliste il faut qu'un été particulièrement court soit suivi d'un hiver particulièrement long pour garder plus ou moins la périodicité annuelle.

Complément

    En prenant la dérivée de (10) par rapport à \(x_I\), on obtient \begin{align} \frac{\partial^2 \phi^{(k,h)}}{\partial t \, \partial x_I} =& \sum_{i,j} \left [ A^{(k)}_{i,j} \delta_{j,I} (x_i-1) + \left (A^{(k)}_{i,j} x_j - B^{(k)}_{i,j}\right ) \delta_{i,I} \right ] \frac{\partial \phi^{(k,h)}}{\partial x_j} \nonumber\\ &+ \sum_{i,j} \left (A^{(k_n)}_{i,j} x_j - B^{(k_n)}_{i,j}\right ) (x_i-1) \frac{\partial^2 \phi^{(k,h)}}{\partial x_I \partial x_j}\, .\tag{16} \end{align} \(\delta\,\) est le symbole de Kronecker. On prend \(\,x_1=\cdots=x_m=1\). On obtient \[\frac{\partial}{\partial t} \left [\frac{\partial \phi^{(k,h)}}{\partial x_I}(t,1,\ldots,1)\right ]=\sum_{j} \left (A^{(k)}_{I,j} - B^{(k)}_{I,j}\right ) \frac{\partial \phi^{(k,h)}}{\partial x_j}(t,1,\ldots,1).\] Ceci est identique à (12). On prend la dérivée par rapport à \(\,x_J\,\) de (16). On prend une nouvelle fois \(\,x_1=\cdots=x_m=1\). On obtient \begin{align} \frac{\partial}{\partial t}\left [\frac{\partial^2 \phi^{(k,h)}}{\partial x_I \partial x_J} (t,1,\ldots,1)\right ] = & A^{(k)}_{J,I} \frac{\partial \phi^{(k,h)}}{\partial x_I}(t,1,\ldots,1) \nonumber\\ &+ A^{(k)}_{I,J} \frac{\partial \phi^{(k,h)}}{\partial x_J}(t,1,\ldots,1) \nonumber\\ &+ \sum_{j} \left (A^{(k)}_{I,j} - B^{(k)}_{I,j}\right ) \frac{\partial^2 \phi^{(k,h)}}{\partial x_j \partial x_J}(t,1,\ldots,1)\nonumber\\ &+ \sum_{j} \left (A^{(k)}_{J,j} - B^{(k)}_{J,j}\right ) \frac{\partial^2 \phi^{(k,h)}}{\partial x_I \partial x_j}(t,1,\ldots,1)\, . \tag{17} \end{align} Un calcul semblable se trouve par exemple dans le § V.7.3 du livre d'Athreya et Ney (1972). Rappelons les notations (11) et (13) pour les dérivées premières et secondes. On définit \[G_{i,j}^{(k,h)}(t)=A_{i,j}^{(k)} M^{(k,h)}_j(t)+A_{j,i}^{(k)} M^{(k,h)}_i(t)\ , \quad G^{(k,h)}(t)=\left (G_{i,j}^{(k,h)}(t)\right )_{i,j} .\] Alors (17) est identique à \[\frac{dS^{(k,h)}_{I,J}}{dt}(t) = \sum_j \left [C_{I,j}^{(k)} S^{(k,h)}_{j,J}(t) + C_{J,j}^{(k)} S^{(k,h)}_{j,I}(t)\right ] + G_{I,J}^{(k,h)}(t),\quad t > 0.\] On utilise la symétrie de la matrice \(\,S^{(k,h)}(t)\,\). Cette équation devient \[\frac{d S^{(k,h)}}{dt}(t) = C^{(k)} S^{(k,h)}(t) + S^{(k,h)}(t) \left (C^{(k)}\right )^* + G^{(k,h)}(t)\, .\] \(^*\,\) désigne la matrice transposée. Mais \(\,\phi^{(k,h)}(0,x_1,\ldots,x_m)=x_h.\) On a donc \(S^{(k,h)}(0)=0\). Comme dans le livre d'Athreya et Ney (1972, formule (15), p. 203), on obtient \begin{equation}\tag{18} S^{(k,h)}(t)= \int_{0}^{t} e^{(t-u)C^{(k)}} G^{(k,h)}(u) \left (e^{(t-u)C^{(k)}} \right )^* du, \quad \forall \, t\geq 0. \end{equation} On remarque

• \(M^{(k,h)}_i(t) > 0\,\) pour tout i et tout t>0,
• par hypothèse, il existe \((i,j)\) avec \(A^{(k)}_{i,j} > 0\).

Remerciements

    On remercie le professeur Khaladi pour ses encouragements. On remercie aussi les professeurs Ball et Bansaye et particulièrement le professeur Jagers pour leurs commentaires sur certaines parties de ce travail.

Références bibliographiques