J. Math. Biol. 71 (2015) p. 491–511
Nicolas Bacaër
Institut de recherche pour le développement, Bondy, France
Université Pierre et Marie Curie, Les Cordeliers, Paris, France
nicolas.bacaer@ird.fr
Dans le modèle stochastique SIS pour une épidémie avec un taux de contact a, un taux de guérison b < a et une taille de population N, le temps moyen jusqu'à extinction τ est tel que \((\log \tau)/N\) converge vers \(c=b/a-1-\log(b/a)\) lorsque N converge vers l'infini. Cet article considère le cas plus réaliste où le taux de contact est une fonction périodique dont la moyenne est supérieure à b. \((\log \tau)/N\) converge vers une nouvelle limite C, qui est liée à une équation de Hamilton-Jacobi périodique. Lorsque le taux de contact est une fonction cosinus avec une petite amplitude, avec une grande fréquence ou avec une fréquence très petite, on peut obtenir des formules approchées pour C de manière analytique comme dans [Assaf et coll., 2008, Phys Rev E 78, 041123]. Ces résultats sont illustrés par des simulations numériques.
Le modèle stochastique SIS pour une épidémie a été étudié en détail lorsque l'environnement est supposé constant, comme dans le livre de Nåsell (2011). Avec un taux de contact rate a, un taux de guérison b < a et une taille de population N, le temps moyen jusqu'à extinction τ (partant par exemple d'une personne infectée) est tel que \begin{equation}\tag{1} \frac{\log \tau}{N} \mathop{\longrightarrow}_{N\to +\infty} c=b/a-1-\log(b/a) > 0\, \end{equation} (Nåsell, 2011, théorème 12.1). Parmi d'autres références, voir aussi (Andersson et Djehiche, 1998), (Doering et coll., 2005) et (Assaf et Meerson, 2010). Ces derniers utilisent la méthode de Brillouin, Kramers et Wentzel [BKW]. La probabilité \(P_n(t)\ \) d'avoir n≥ 1 personnes infectées au temps t s'approche d'abord d'une distribution quasi-stationnaire \(\pi_n\). On définit \(x=n/N\) de sorte que \(0\leq x\leq 1\). Lorsque N converge vers l'infini, \(-(\log \pi_n)/N\) s'approche d'une fonction continue \(S(x)\) avec l'équation de Hamilton-Jacobi stationnaire \[H\left (x,\frac{\partial S}{\partial x}\right )=0\] avec \begin{align} H(x,p)&=a x (1-x) (e^p - 1) +b x (e^{-p}-1)\nonumber\\ &= x (1 -e^{-p}) [a(1-x)e^p - b ] \tag{2} \end{align} (Assaf et Meerson, 2010, (12) et §IV.D.3). Plus précisément, la branche de la ligne de niveau H=0 avec \(a(1-x)e^p - b=0\) conduit à la formule \begin{equation}\tag{3} S(x)=x \log(b/a) + x + (1-x)\log(1-x) + \mathrm{constante}\, . \end{equation} Cette fonction a un minimum lorsque \(x=x^*=1-b/a\ \), avec \(x^* > 0\) parce que \(b < a\). Finalement \[c=S(0)-S(x^*)\] est la hauteur entre le fond et le bord à x=0 du puits de potentiel \(S(x)\). De manière équivalente, le système hamiltonien \begin{equation}\tag{4} \frac{dx}{dt} = \frac{\partial H}{\partial p},\quad \frac{dp}{dt} = -\frac{\partial H}{\partial x} \end{equation} a une orbite hétérocline qui relie \((x^*,0)=(1-\frac{b}{a},0)\) et \((0,p^*)=(0,\log\frac{b}{a})\). Le nombre c est égal à l'action \[\int_{x^*}^0 p\, dx\] le long de cette orbite. La méthode BKW a été utilisée pour d'autres processus de naissance et de mort en physique ou en biologie des populations (Ovaskainen et Meerson, 2010 ; Kamenev, 2011).
Dans leur étude d'une réaction chimique avec branchement et annihilation, (Escudero et Rodríguez, 2008) a montré comment un environnement périodique en temps influençait l'orbite hétérocline qui joue un rôle central pour le temps moyen d'extinction. (Assaf et coll., 2008) a étudié le même modèle plus en détail, calculant notamment la correction au temps moyen d'extinction due à une perturbation périodique de petite amplitude, de basse fréquence ou de haute fréquence. Ces auteurs ont obtenu des formules générales qui peuvent être appliquées à d'autres processus de naissance et de mort présentant une métastabilité. Par ailleurs, (Billings et coll., 2013, figure 7) montre des simulations Monte-Carlo d'un modèle stochastique SIS périodique.
L'objectif ici est d'appliquer la méthode BKW utilisée par (Assaf et coll., 2008) au modèle épidémique SIS avec un taux de contact périodique de période T, dont la moyenne est supérieure à b. Un tel modèle peut représenter par exemple la propagation d'une infection bactérienne qui ne confère pas d'immunité. La propagation peut avoir lieu dans une école avec une périodicité hebdomadaire (liée aux fins de semaine), ou une périodicité annuelle (liée aux vacances et à la saisonnalité). Il s'agit bien sûr seulement d'une première étape vers des modèles plus réalistes.
Dans la section 2, des calculs informels suggèrent que le temps moyen d'extinction \(\tau\) (partant par exemple d'une personne infectée au temps 0) est tel que \begin{equation}\tag{5} \frac{\log \tau}{N} \mathop{\longrightarrow}_{N\to +\infty}C = \min_{0\leq t \leq T} S^*(t,0^+)- \min_{0\leq t \leq T} \, \min_{0\leq x\leq 1} S^*(t,x) \, . \end{equation} Ici, \(S^*(t,x)\) est une solution de viscosité, périodique de période T, de l'équation de Hamilton-Jacobi \begin{equation}\tag{6} \frac{\partial S}{\partial t}+H\left (t,x,\frac{\partial S}{\partial x}\right )=0,\quad 0 < x < 1, \end{equation} avec la condition aux bords mixte Dirichlet-« état contraint» \[S(t,0)=0,\quad \frac{\partial S}{\partial x}(t,1)=+\infty.\] \(S(t,x)\) ne doit pas être identiquement nulle près de x=0. La condition aux bords doit être entendue au sens de viscosité (Barles, 1994) parce que \(S^*(t,0^+)\) peut ne pas être égal à 0. Le hamiltonien \(H(t,x,p)\) est identique à (2) sauf que le paramètre constant \(a\) est remplacé par \(a(t)\). Avec \[a(t)=a_0(1+\varepsilon \cos(\omega t)),\quad \omega=2\pi/T, \quad a_0 > b, \quad |\varepsilon|\leq 1,\] on définit \(c_0=b/a_0-1-\log(b/a_0)\). Suivant les méthodes de (Assaf et coll., 2008), la section 2 montre que \[ C\simeq c_0- \frac{\pi\, \omega\, |\varepsilon| }{a_0 \sinh \left (\frac{ \pi \omega}{a_0-b}\right )} \] si \(\varepsilon\) est proche de 0, \[C\simeq c_0 - |\varepsilon| (1-b/a_0)\] si \(\omega\ll a_0\) et \[ C\simeq c_0 - \frac{ (a_0-b)^2 \varepsilon^2}{12\ \omega^2} (1 + 2b/a_0) \] dans la limite haute-fréquence \(\omega\gg a_0\). On peut conjecturer que \(C > 0\) tant que \(\frac{1}{T} \int_0^T a(t)\, dt > b\). \(C\) est probablement toujours inférieur à \(c_0\,\), parce que les variations saisonnières tendent à favoriser l'extinction des maladies infectieuses. Ceci suggère plus précisément qu'un environnement périodique conduit pour le modèle SIS à une décroissance exponentielle du temps moyen d'extinction semblable à celle obtenue pour le modèle de branchement et annihilation (Assaf et coll., 2008). La section 3 illustre ces résultats avec des simulations numériques. La section 4 ajoute quelques remarques.
Équation maîtresse et théorie de Floquet. N est la population totale, supposée constante. On définit
\(P_n(t)\) est la probabilité que \(I(t)=n\,\). On a \begin{align} \frac{dP_n}{dt} = a(t) (n-1)(1-(n-1)/N) P_{n-1} &-[a(t) n(1-n/N)+b\, n ] P_n + b(n+1) P_{n+1},\quad 0\leq n\leq N. \tag{7} \end{align} Ici, \(P_{-1}=0\) et \(P_{N+1}=0\). Bien sûr, \[\sum_{n=0}^N P_n(t)=1.\] Le système (7) s'écrit aussi \[\frac{dP}{dt} = M(t)\, P.\] \(P(t)\) est le vecteur \((P_n(t))_{0\leq n\leq N}\) et \(M(t)\) est la matrice carrée de taille N+1 \[ M(t)=\left ( \begin{array}{cccccc} 0 & b & 0 & 0 & \cdots & 0\\ 0 & -b-a(t)(1-\frac{1}{N}) & 2b &0 & \cdots& 0\\ 0 & a(t) (1-\frac{1}{N}) & -2b-2a(t)(1-\frac{2}{N}) & 3b& \cdots& 0\\ \vdots & \vdots & \vdots & \vdots & & \vdots\\ 0 & 0 & 0 & 0 & \cdots & -bN \end{array} \right ). \] Cette matrice a la structure par blocs \[M(t)=\left (\begin{array}{c|c} 0 & \ast \\ \hline 0 & Q(t) \end{array}\right ).\] \(Q(t)\) est une matrice carrée de taille N. \(X(t)\) et \(Y(t)\) sont les matrices avec \[\frac{dX}{dt} = M(t)\, X,\quad X(0)=I_{N+1}\] \[\frac{dY}{dt}=Q(t)\, Y,\quad Y(0)=I_N.\] \(I_N\) est la matrice identité de taille N. Les multiplicateurs de Floquet de \(M(t)\,\), c'est-à-dire les valeurs propres de la matrice de monodromie \(X(T)\) sont \(\{\mu_0=1\}\) et les multiplicateurs de Floquet de \(Q(t)\). La matrice \(Q(t)\) est coopérative: les coefficients en dehors de la diagonale sont positifs ou nuls. Cette matrice est aussi irréductible parce que les éléments juste au-dessus et en-dessous de la diagonale sont tous strictement positifs. Par conséquent, tous les éléments de \(Y(t)\) sont strictement positifs pour \(t > 0\). D'après le théorème de Perron et Frobenius, la valeur propre \(\mu_1\) de \(Y(T)\) avec la partie réelle la plus grande est un nombre réel strictement positif et le sous-espace propre associé est de dimension 1. De plus, \[(1\ 1 \ldots 1)Q(t)=(-b\ 0\ 0\ \ldots 0).\] On a \(0 < \mu_1 < 1\, \) (Aronsson et Kellogg, 1978) et \(\lambda_1=(\log \mu_1)/T < 0\). Le vecteur \((1,0,0,\ldots,0)\) est un état stationnaire. \(P(t)\) converge vers ce vecteur si \(t\to +\infty\). L'objectif ici est d'estimer, pour N grand, la proximité entre \(\lambda_1\) et 0.
Soit v un vecteur propre de \(X(T)\) associé à la valeur propre \(\mu_1=e^{\lambda_1 T}\). On peut choisir v de sorte que \(v_n > 0, \ 1\leq n\leq N\). On a ainsi \[X(T)v=e^{\lambda_1 T} v.\] Comme dans la théorie de Floquet, on définit \[\pi(t)=e^{-\lambda_1 t} X(t) v.\] On a alors \[\frac{d\pi}{dt}(t)= -\lambda_1 \pi(t) + M(t) \pi(t).\] De plus \[\pi(T)=e^{-\lambda_1 T} X(T) v=v=\pi(0).\] Donc \(\pi(t)\) est une fonction périodique de période T. Avec \(\pi(t)=(\pi_n(t))_{0\leq n\leq N}\,\), on a \begin{align} \lambda_1 \pi_n + \frac{d\pi_n}{dt} = a(t) (n-1)(1-(n-1)/N) \pi_{n-1} &-[a(t) n(1-n/N)+b\, n ] \pi_n + b(n+1) \pi_{n+1} \, .\tag{8} \end{align} En sommant ces équations, on obtient \[\lambda_1 \sum_{n=0}^N \pi_n(t) + \frac{d}{dt} \sum_{n=0}^N \pi_n(t) = 0.\] On a donc \[\sum_{n=0}^N \pi_n(t)=e^{-\lambda_1 t} \sum_{n=0}^N \pi_n(0).\] Mais \(\sum_{n=0}^N \pi_n(t)\) est une fonction périodique de période T. Par conséquent \(\sum_{n=0}^N \pi_n(0)=0\) et \(\sum_{n=0}^N \pi_n(t)=0\ \forall t\). On a donc \[\pi_0(t)=-\sum_{n=1}^N \pi_n(t).\] Mais (8) avec \(n=0\) montre aussi que \[\lambda_1 \pi_0(t) + \frac{d\pi_0}{dt} = b\, \pi_1(t).\] Parce que \(\pi_0(t)\) est périodique, on obtient en intégrant \begin{equation}\tag{9} \lambda_1 = b\, \frac{\int_0^T \pi_1(t)\, dt}{\int_0^T \pi_0(t)\, dt} = -b\, \frac{\int_0^T \pi_1(t)\, dt}{\sum_{n=1}^N \int_0^T \pi_n(t)\, dt}\, . \end{equation}
Solution BKW et équation de Hamilton-Jacobi. Lorsque N est grand, cherchons une solution BKW \[\pi_n(t)\simeq e^{-N S(t,x)},\quad 1\leq n\leq N,\] avec \(x=n/N\). \(S(t,x)\) est une fonction continue de t et x si (\,0 < x < 1\), qui est périodiquede période T par rapport à t. On a alors \begin{align*} \frac{d\pi_n}{dt} &\simeq -N\, \frac{\partial S}{\partial t}(t,x) \, e^{-N S(t,x)}\, ,\\ \pi_{n+1}(t) &\simeq e^{-N S(t,x+\frac{1}{N})} \simeq e^{-N S(t,x) - \frac{\partial S}{\partial x}(t,x)},\quad \pi_{n-1}(t) \simeq e^{-N S(t,x) + \frac{\partial S}{\partial x}(t,x)}. \end{align*} On définit \(\alpha(t,x)=a(t)x(1-x)\) et \(\beta(x)=b\, x\). Alors (8) s'écrit \[\lambda_1 \pi_n + \frac{d\pi_n}{dt} = N \alpha(t,x-1/N) \pi_{n-1} -N [\alpha(t,x)+\beta(x) ] \pi_n + N \beta(x+1/N) \pi_{n+1} \, .\] En ne gardant que les expressions dominantes, on peut utiliser \(\alpha(t,x-1/N)\simeq \alpha(t,x)\) et \(\beta(x+1/N)\simeq \beta(x)\) pour obtenir \[\lambda_1 \pi_n + \frac{d\pi_n}{dt} \simeq N \alpha(t,x) [\pi_{n-1} - \pi_n] + N \beta(x) [\pi_{n+1} - \pi_{n}] \, .\] \(\lambda_1\) est probablement exponentiellement petit. On peut le négliger du côté gauche. En injectant la forme BKW et en divisant par \(N\, e^{-N S(t,x)}\,\), on obtient l'équation de Hamilton-Jacobi \begin{equation}\tag{10} \frac{\partial S}{\partial t} + a(t) x (1-x) \left [ e^{\frac{\partial S}{\partial x}}-1 \right ] + b\, x \left [e^{-\frac{\partial S}{\partial x}}-1 \right ]= 0\, ,\quad 0 < x < 1. \end{equation} Ceci est de la forme (6) avec un hamiltonian périodique \(H(t,x,p)\) donné par (2), et \(a(t)\) remplace \(a\). Des équations telles que (10) ont normalement des solutions asymptotiques de la forme \(S(t,x)=-Et+\Sigma(t,x)\). \(\Sigma(t,x)\) est une fonction périodique de période T par rapport à t et E est une constante. Ici cependant, seules les solutions avec \(E=0\) présentent un intérêt: elles correspondent aux orbites hétéroclines de la section 2.2 ci-dessous.
Conditions aux bords. Parce que \(H(t,0,p)=0\,\), on a \(\frac{\partial S}{\partial t}(t,0)=0\). \(S(t,0)\) est donc une constante \(S_0\) indépendante de t. Comme (10) ne fait intervenir que des dérivées partielles du premier ordre, ses solutions sont définies à une constante additive près (rappelons que le vecteur propre v de \(X(T)\) est défini à une constante multiplicative près). On peut donc choisir \(S_0=0\), d'où la condition de Dirichlet: \begin{equation}\tag{11} S(t,0)=0\quad \forall t. \end{equation} De plus, parce que \(\pi_n(t)=0\ \forall n > N\) et parce que la formule (3) dans un environnement constant montre que \(|S(1)|<+\infty\) tandis que \(\frac{dS}{dx}(1)=+\infty\,\), on impose que \begin{equation}\tag{12} \frac{\partial S}{\partial x}(t,1)=+\infty\quad \forall t. \end{equation} Une autre manière de présenter cette condition au bord est la « contrainte d'état» \[\frac{\partial S}{\partial t}+H\left (t,x,\frac{\partial S}{\partial x}\right )\geq 0\] si x=1. Cette condition conduit avec x=1 à \[\frac{\partial H}{\partial p}(t,x,\frac{\partial S}{\partial x})\geq 0\] (Soner, 1986). Mais parce que \[\frac{\partial H}{\partial p}(t,x,p)=a(t)x(1-x)e^p-bxe^{-p},\] cette expression est positive ou nulle en x=1 si et seulement si \(p=+\infty\,\), comme dans (12).
Propriétés du hamiltonien. \(H(t,x,p)\) est convexe en p parce que \[\frac{\partial^2 H}{\partial p^2}(t,x,p)=a(t)\, x (1-x)\, e^p + b\, x\, e^{-p}\geq 0.\] De plus, \(H(t,x,p)\to +\infty\) si \(|p|\to +\infty\) pourvu que \(0 < x < 1\). Mais cette propriété n'est plus vraie quand \(x=0\) ou bien \(x=1\). On a \(H(t,x,0)=0\). Le lagrangien est \[L(t,x,v)=\max_p \{ pv-H(t,x,p)\}.\] On a avec \(0 < x < 1\,\) \[L(t,x,v)=p_*v-H(t,x,p_*).\] \(p_*\) est l'unique solution de \[v=\frac{\partial H}{\partial p}(t,x,p_*)=a(t)x(1-x)e^{p_*}-bxe^{-p_*}.\] C'est une équation polynomiale de degré 2 en \(e^{p_*}\). Cela donne \begin{align*} L(t,x,v) &=p_*v-a(t)x(1-x)(e^{p_*}-1)-bx(e^{-p_*}-1)\\ &= v \log \left (\frac{v+\sqrt{v^2+4a(t)x(1-x)bx}}{2a(t)x(1-x)}\right )+a(t)x(1-x)+bx\\ &\quad -\frac{v+\sqrt{v^2+4a(t)x(1-x)bx}}{2} - \frac{2a(t) x(1-x) bx}{v+\sqrt{v^2+4a(t)x(1-x)bx}}\, . \end{align*} Pour x=1, on a
Solutions de l'équation de Hamilton-Jacobi. Pour une condition initiale donnée \(S_0(x)\), la fonction \begin{align*} S(t,x)=\inf \Bigl \{ &\int_\theta^t\!\!\! L(s,\xi(s),\dot{\xi}(s))\, ds+1_{\theta=0}\, S_0(\xi(\theta))\, ;\\ &0\leq \theta\leq t,\ \xi\in C^1([\theta,t];[0,1]),\ \theta=0\ \vee\ \xi(\theta)=0,\ \xi(t)=x\Bigr \} \end{align*} est une solution de viscosité de (10) avec les conditions mixtes (11)-(12) aux bords, et avec \(S(0,x)=S_0(x)\) (Barles, 1994). C'est la fonction valeur d'un problème de temps de sortie en \(x=0\) avec la « contrainte d'état» en \(x=1\). Une solution périodique \(S^*(t,x)\) de (10)-(11)-(12) est ainsi donnée par un point fixe de l'opérateur d'évolution ci-dessus: \(S^*(0,x)=S^*(T,x)\). (Roquejoffre, 2001) et (Mitake, 2009) ont étudié de semblables équations de Hamilton-Jacobi périodiques avec des conditions aux bords du type de Dirichlet. Noter cependant qu'il n'y a pas d'unicité. Pour des problèmes reliés, voir (Barles et Perthame, 1988). En effet, considérons le cas spécial où \(a(t)=a_0\) est constant. Dans ce cas, il y a deux types de solutions de viscosité stationnaires \(S^*(x)\).
Comportement de \(\lambda_1\) si N est grand. Retournant à (9), on a \[ \frac{\log(-\lambda_1)}{N} = \frac{\log b}{N} + \frac{1}{N} \log \left (\int_0^T \pi_1(t)\, dt \right )- \frac{1}{N} \log \left (\sum_{n=1}^N \int_0^T \pi_n(t)\, dt\right )\, .\] On a \[\pi_1(t)\simeq e^{-N S^*(t,1/N)}\simeq e^{-N S^*(t,0^+)}\] pour N grand. On a donc \[ \frac{1}{N} \log \left (\int_0^T \pi_1(t)\, dt \right )\mathop{\longrightarrow}_{N \to +\infty} -\min_{0\leq t \leq T} S^*(t,0^+)\] à cause de la formule de Laplace pour l'évaluation asymptotique des intégrales. De même, parce que \(\pi_n(t)\simeq e^{-N S^*(t,n/N)}\,\), on a \begin{align*} \frac{1}{N} \log \left (\sum_{n=1}^N \int_0^T \pi_n(t)\, dt \right )&\mathop{\longrightarrow}_{N \to +\infty} - \min_{0\leq t\leq T} \, \min_{0\leq x\leq 1} S^*(t,x) \end{align*} et \[\frac{\log(-\lambda_1)}{N} \mathop{\longrightarrow}_{N\to +\infty} -C\] avec Cdonné par (5). On peut conjecturer que \(C > 0\) si et seulement si \(\frac{1}{T} \int_0^T a(t)\, dt > b\).
Temps moyen d'extinction. En partant de n personnes infectées au temps t, le temps moyen d'extinction \(\tau_n(t)\) est une solution périodique de période T du système \begin{equation}\tag{13} -1=\frac{d\tau_n}{dt} + b\, n \tau_{n-1} - (a(t) n (1-n/N)+b\, n) \tau_n + a(t) n (1-n/N) \tau_{n+1},\quad 1\leq n\leq N, \end{equation} avec \(\tau_0(t)=0\). Ce système fait intervenir la matrice transposée \(Q^*(t)\) de la matrice \(Q(t)\). On définit
Cas général. Rappelons que l'équation de Hamilton-Jacobi (6) peut être résolue au moins localement par tracé de rayons, c'est-à-dire, en résolvant simultanément le système hamiltonien (4) et l'équation \[\frac{dz}{dt}=p(t) \frac{\partial H}{\partial p}(t,x(t),p(t)) - H(t,x(t),p(t))\] avec les conditions initiales \(x(0)=x_0\), \(p(0)=\frac{\partial S}{\partial x}(0,x_0)\), \(z(0)=S(0,x_0)\), de sorte que \(z(t)=S(t,x(t))\). En suivant (Assaf et coll., 2008), considérons de plus près le système hamiltonien (4). Dans le cas présent, \begin{align} \frac{\partial H}{\partial p}(t,x,p)&=a(t)x(1-x)e^p - b x e^{-p},\tag{14}\\ \frac{\partial H}{\partial x}(t,x,p)&=a(t)(1-2x)(e^p-1)+b(e^{-p}-1)\, .\nonumber \end{align}
Cherchons d'abord une solution non triviale périodique de période T, avec \(x\equiv 0\) et \[ \frac{dp}{dt} = - \frac{\partial H}{\partial x}(t,0,p)= - (a(t) - b\, e^{-p}) (e^p-1)\, . \] Avec \(p = \log (1+q)\,\), on obtient une équation différentielle de Bernoulli qui peut être facilement résolue. Cela donne la solution périodique de période T \[p^*(t)= \log \left ( 1 + \left [ \frac{e^{-bt +\int_0^t a(s)\, ds}}{e^{p^*(0)}-1} + \int_0^t a(s)\, e^{-b(t-s) + \int_s^t a(u)\, du} ds\right ]^{-1} \right )\, , \] avec \[p^*(0)=\log \left (1+\frac{1-e^{-bT+\int_0^T a(s)\, ds}}{\int_0^T a(s)\, e^{-b(T-s)+\int_s^T a(u)\, du} ds}\right )\, .\] La solution périodique \((0,p^*(t))\) est instable. En effet, avec \(x(t)=\tilde{x}(t)\) et \(p(t)=p^*(t)+\tilde{p}(t)\) et en linéarisant les équations, on obtient \[\left (\begin{array}{c} d\tilde{x}/dt \\ d\tilde{p}/dt \end{array} \right )= \left ( \begin{array}{ccc} a(t) e^{p^*(t)} - b e^{-p^*(t)} &\quad& 0 \\ 2a(t)(e^{p^*(t)}-1) &\quad& -a(t) e^{p^*(t)} + b e^{-p^*(t)} \end{array} \right ) \left ( \begin{array}{c} \tilde{x} \\ \tilde{p} \end{array} \right ).\] Les multiplicateurs de Floquet sont \[f=\exp \int_0^T [a(t) e^{p^*(t)}-b e^{-p^*(t)}] dt\] et \(1/f\,\), d'où l'instabilité. L'instabilité peut aussi être vue comme une conséquence du théorème de Liouville concernant l'invariance du « volume» dans l'espace de phase (x,p) sous l'action du flot hamiltonien.
Deuxièmement, cherchons une solution non triviale, périodique de période T, avec \(p\equiv 0\) et \[\frac{dx}{dt} = \frac{\partial H}{\partial p}(t,x,0) = a(t) x (1-x) - b x\, .\] C'est l'équation de champ moyen du modèle SIS. L'unique solution périodique non nulle est \[x^*(t)=\left ( \frac{1}{x^*(0)} \, e^{bt-\int_0^t a(s)\, ds} + \int_0^t a(u)\, e^{b(t-u)-\int_u^t a(s)\, ds} du \right )^{-1}\] avec \begin{equation}\tag{15} x^*(0)=\frac{1-e^{bT-\int_0^T a(s)\, ds}}{\int_0^T a(u)\, e^{b(T-u)-\int_u^T a(s)\, ds}\, du}\, . \end{equation} La solution périodique \((x^*(t),0)\) est également instable. En effet, avec \(x(t)=x^*(t)+\tilde{x}(t)\) et \(p(t)=\tilde{p}(t)\) et en linéarisant les équations, on obtient \[\left (\begin{array}{c} d\tilde{x}/dt \\ d\tilde{p}/dt \end{array} \right )= \left ( \begin{array}{ccc} a(t) (1-2x^*(t)) - b &\quad & a(t)x^*(t)(1-x^*(t))+b x^*(t) \\ 0 &\quad & -a(t) (1-2x^*(t)) + b \end{array} \right ) \left ( \begin{array}{c} \tilde{x} \\ \tilde{p} \end{array} \right ).\] Les multiplicateurs de Floquet sont une nouvelle fois inverses l'un de l'autre, d'où l'instabilité.
Rappelons de la section 1 que dans un environnement constant, il y a une orbite hétérocline dans le plan de phase (x,p) reliant les points stationnaires \((x^*,0)=(1-b/a,0)\) et \((0,p^*)=(0,\log(b/a))\) si \(a > b\). (Escudero et Rodríguez, 2008) a trouvé une orbite hétérocline semblable pour le modèle périodique de branchement et annihilation de particules identiques, au moins pour une petite amplitude de la perturbation périodique. Donc on peut espérer l'existence d'une orbite hétérocline \((\hat{x}(t),\hat{p}(t))\,\), qui relie les solutions périodiques \((x^*(t),0)\) et \((0,p^*(t))\). L'existence peut probablement être démontrée en utilisant une approche variationnelle (Rabinowitz, 1994). Cette orbite spéciale peut être obtenue numériquement par une méthode de tir. D'après (Assaf et coll., 2008, équation (20)), \begin{equation}\tag{16} C=\int_{-\infty}^{+\infty} \left [ \hat{p}(t) \frac{\partial H}{\partial p}(t,\hat{x}(t),\hat{p}(t)) - H(t,\hat{x}(t),\hat{p}(t))\right ] dt\, . \end{equation} Cette intégrale peut être évaluée numériquement.
Méthode de perturbation. Si la fonction \(a(t)\) est une constante \(a_0\,\), alors \((\hat{x}_0(t),\hat{p}_0(t))\) est l'orbite hétérocline reliant les points stationnaires \((x^*,0)=(1-b/a_0,0)\) et \((0,p^*)=(0,\log(b/a_0))\). Cette orbite est telle que \(a_0(1-x)e^p-b =0\), comme on peut le voir avec (2). En utilisant cette équation pour exprimer p en fonction de x et en insérant le résultat dans la première équation de (4), on obtient \[\frac{dx}{dt}=b\, x - a_0 x (1-x).\] La solution est \[x(t)=\left [ \frac{1}{x(t_0)} e^{(a_0-b)(t-t_0)} + \frac{a_0}{a_0-b} (1-e^{(a_0-b)(t-t_0)}) \right ]^{-1}.\] En choisissant par exemple \(x(t_0)=(1-b/a_0)/2\,\), on obtient \[\hat{x}_0(t)=\frac{1-b/a_0}{1+e^{(a_0-b)(t-t_0)}}\quad \mathrm{et}\quad \hat{p}_0(t)= \log \frac{1+e^{(a_0-b)(t-t_0)}}{1+e^{(a_0-b)(t-t_0)} a_0/b}\, .\]
Supposons maintenant que \[a(t)=a_0 (1+ \varepsilon\, \phi(t))\] avec \(a_0 > b\), \(\varepsilon\) petit et \(\phi(t)\) une fonction périodique avec \(\int_0^T \phi(t)\, dt=0\). L'hamiltonien peut être écrit sous la forme \[H(t,x,p)=H_0(x,p)+\varepsilon\, H_1(t,x,p).\] \(H_0(x,p)\) est identique à (2), sauf que \(a_0\) remplace \(a\,\). \[H_1(t,x,p)=a_0\, \phi(t)\, x (1-x) (e^p-1).\] Avec \(c_0=b/a_0-1-\log(b/a_0)\), \[C \simeq \min_{t_0} \Gamma(t_0),\quad \Gamma(t_0)=c_0 - \varepsilon \int_{-\infty}^{+\infty} H_1(t,\hat{x}_0(t),\hat{p}_0(t))\, dt,\quad \varepsilon\simeq 0\] (Assaf et coll., 2008, équation (24)). Dans le cas présent, \((1-\hat{x}_0)e^{\hat{p}_0} = b/a_0\). On a donc \begin{align*} \Gamma(t_0) &=c_0 - \varepsilon\, a_0 \int_{-\infty}^{+\infty} \phi(t)\, \hat{x}_0(t) \left [b/a_0 -1 +\hat{x}_0(t)\right ] dt \\ &= c_0+\varepsilon (1-b/a_0) \int_{-\infty}^{+\infty} \phi(t_0+u/(a_0-b)) \frac{e^u}{(1+e^u)^2}\, du\, . \end{align*} \(\Gamma(t_0)\) est ainsi une fonction périodique de \(t_0\) avec \(\int_0^T \Gamma(t_0)\, dt_0=0\). Considérons la décomposition de Fourier de \(\phi(t)\), \[\phi(t)=\sum_{k=-\infty}^{+\infty} \phi_k \, e^{ k\, \mathrm{i} \omega t},\] avec \(\omega=2\pi/T\), \(\phi_0=0\) parce que la moyenne de \(\phi(t)\) est nulle, et \(\phi_{-k}=\bar{\phi_k}\) (nombre complexe conjugué). On a alors \begin{align*} \Gamma(t_0)&= c_0+\varepsilon (1-b/a_0) \sum_{k=-\infty}^{+\infty} \phi_k \, e^{ k\, \mathrm{i} \omega t_0} \int_{-\infty}^{+\infty} \!\!\! e^{\frac{ k\, \mathrm{i} \omega u}{a_0-b}} \frac{e^u}{(1+e^u)^2}\, du\\ &= c_0+\varepsilon (1-b/a_0) \sum_{k=-\infty}^{+\infty} \phi_k \, e^{ k\, \mathrm{i} \omega t_0} \frac{\frac{ k \pi \omega}{a_0-b}}{\sinh \left (\frac{k \pi \omega}{a_0-b}\right )} \end{align*} (voir Appendice). En particulier si \(\phi(t)=\cos(\omega t)\,\), on a \(\phi_{\pm 1}=1/2\) et \(\phi_k=0\) sinon. On a donc \begin{equation}\tag{17} \Gamma(t_0)=c_0+\varepsilon \frac{\pi \omega \cos( \omega t_0)}{a_0 \sinh \left (\frac{\pi \omega}{a_0-b}\right )}\, . \end{equation}
Comme (Escudero et Rodríguez, 2008) et (Assaf et coll., 2008), le système perturbé est de la forme \begin{equation}\tag{18} \frac{dx}{dt} = \frac{\partial H_0}{\partial p}+\varepsilon \frac{\partial H_1}{\partial p},\quad \frac{dp}{dt} = -\frac{\partial H_0}{\partial x}-\varepsilon \frac{\partial H_1}{\partial x}\, . \end{equation} \(\hat{x}_0(t)\) et \(\hat{p}_0(t)\) ne dépendent que de \(t-t_0\). Donc la fonction de Melnikov est \begin{align*} \mathcal{M}(t_0)&=\int_{-\infty}^{+\infty} \! \left [ - \frac{\partial H_1}{\partial x} \frac{\partial H_0}{\partial p} + \frac{\partial H_1}{\partial p} \frac{\partial H_0}{\partial x} \right ]\!\!(t,\hat{x}_0(t),\hat{p}_0(t))\ dt\\ &=\int_{-\infty}^{+\infty} \! \left [ - \frac{\partial H_1}{\partial x} \frac{d\hat{x}_0}{dt} - \frac{\partial H_1}{\partial p} \frac{d\hat{p}_0}{dt} \right ]\!\!(t,\hat{x}_0(t),\hat{p}_0(t))\ dt\, \\ &=\int_{-\infty}^{+\infty} \! \left [ \frac{\partial H_1}{\partial x} \frac{d\hat{x}_0}{dt_0} + \frac{\partial H_1}{\partial p} \frac{d\hat{p}_0}{dt_0} \right ]\!\!(t,\hat{x}_0(t),\hat{p}_0(t))\ dt =-\frac{1}{\varepsilon}\, \frac{d\Gamma}{dt_0}\, . \end{align*} En utilisant (17), on obtient \[\mathcal{M}(t_0)= \frac{\pi \omega \sin( \omega t_0)}{a_0 \sinh \left (\frac{\pi \omega}{a_0-b}\right )}\, .\] \(\mathcal{M}(t_0)\) traverse 0 pour \(t_0=k\pi/\omega\) (k un nombre entier). Par conséquent, l'orbite hétérocline existe au moins pour \(\varepsilon\) petit.
Le minimum de \(\Gamma(t_0)\) dans (17) est obtenu pour \(t_0=T/2\) si \(\varepsilon > 0\) et pour \(t_0=0\) si \(\varepsilon < 0\). Dans les deux cas, on obtient \begin{equation}\tag{19} C\simeq c_0- \frac{\pi \omega |\varepsilon|}{a_0 \sinh \left (\frac{\pi \omega}{a_0-b}\right )}\, , \quad \varepsilon\simeq 0, \end{equation} comme annoncé dans l'introduction. Noter que (19) ressemble à l'équation (4.76) de (Kamenev, 2011) obtenue en partant d'un hamiltonien légèrement différent. Si ω est petit (T est grand) de sorte que \(\omega \ll a_0\), alors (19) montre que \begin{equation}\tag{20} C\simeq c_0-|\varepsilon|(1-b/a_0)\, , \end{equation} qui est indépendant de \(\omega\). Cette formule est la même que celle que l'on obtient dans (1) avec \(a=a_0(1-|\varepsilon|)\, :\) \[\frac{b}{a_0(1-|\varepsilon|)} -1 -\log \frac{b}{a_0 (1-|\varepsilon|)} = \frac{b}{a_0} - 1 - \log \frac{b}{a_0} -|\varepsilon|(1-b/a_0)+o(\varepsilon)\, ,\quad \varepsilon\simeq 0. \] Comme dans « l'approximation adiabatique» de (Assaf et coll., 2008, section IV), on s'attend à ce que la formule (20) soit valable non seulement pour \(\varepsilon\simeq 0\,\), mais aussi tant que \(\omega\ll a_0\) et que le côté droit de (20) est positif. Parce que \(\sinh(x)\geq x\ \forall x\geq 0\,\), on peut remarquer que la valeur approchée de Cdonnée par (20) est toujours inférieure à celle donnée par (19).
Limite haute fréquence. Supposons maintenant que \(\omega\gg a_0\), toujours avec \(\phi(t)=\cos(\omega t)\). Le système (18) s'écrit \begin{align*} \frac{dx}{dt} &= \frac{\partial H_0}{\partial p}(x,p) + a_0 \varepsilon \cos(\omega t) x (1-x) e^p\\ \frac{dp}{dt} &= -\frac{\partial H_0}{\partial x}(x,p) - a_0 \varepsilon \cos(\omega t) (1-2x) (e^p-1)\, . \end{align*} Avec la méthode de Kapitsa (Assaf et coll., 2008, §III.B), \[x(t)=X(t)+\xi(t),\quad p(t)=Y(t)+\eta(t),\] où X et Y sont des variables lentes, tandis que ξ et η sont de petites mais rapides oscillations. Les expressions qui oscillent rapidement donnent: \[\frac{d\xi}{dt}\simeq a_0 \varepsilon \cos(\omega t) X (1-X) e^Y,\quad \frac{d\eta}{dt} \simeq - a_0 \varepsilon \cos(\omega t) (1-2X) (e^Y-1)\, .\] On suppose que X et Y sont constants durant une courte oscillation, avec \(T=2\pi/\omega\). On obtient \[\xi(t)\simeq \frac{a_0 \varepsilon}{\omega} \sin(\omega t) X (1-X) e^Y,\quad \eta(t) \simeq - \frac{a_0 \varepsilon}{\omega} \sin(\omega t) (1-2X) (e^Y-1)\, .\] Ceci suggère la transformation \begin{align*} x&=X+\frac{a_0 \varepsilon}{\omega} \sin(\omega t) X (1-X) e^Y\\ p&=Y - \frac{a_0 \varepsilon}{\omega} \sin(\omega t) (1-2X) (e^Y-1) + \frac{a_0^2 \varepsilon^2}{\omega^2} \Phi(t,X,Y)\, . \end{align*} \(\Phi(t,X,Y)\) est choisi pour que la transformation soit presque canonique, c'est-à-dire pour que les crochets de Poisson satisfassent la condition \begin{equation}\tag{21} \{x,p\}=\frac{\partial x}{\partial X} \frac{\partial p}{\partial Y} - \frac{\partial x}{\partial Y} \frac{\partial p}{\partial X} =1+o(a_0^2/\omega^2)\,. \end{equation} Parce que \begin{align*} \{x,p\}&=\left [1+\frac{a_0 \varepsilon}{\omega} \sin(\omega t) (1-2X) e^Y \right ] \left [1-\frac{a_0 \varepsilon}{\omega} \sin(\omega t) (1-2X) e^Y+ \frac{a_0^2 \varepsilon^2}{\omega^2} \frac{\partial \Phi}{\partial Y} \right ]\\ &\quad - \left [ \frac{a_0 \varepsilon}{\omega} \sin(\omega t) X(1-X) e^Y \right ] \left [ 2 \frac{a_0 \varepsilon}{\omega} \sin(\omega t) (e^Y-1) + \frac{a_0^2 \varepsilon^2}{\omega^2} \frac{\partial \Phi}{\partial X} \right ], \end{align*} la condition (21) s'écrit \begin{align*} \{x,p\}&=1-\frac{a_0^2 \varepsilon^2}{\omega^2} \sin^2(\omega t) (1-2X)^2 e^{2Y} + \frac{a_0^2 \varepsilon^2}{\omega^2}\frac{\partial \Phi}{\partial Y} \\ &\quad - 2\frac{a_0^2 \varepsilon^2}{\omega^2} \sin^2(\omega t) X(1-X) e^{Y}(e^Y-1) + o(a_0^2/\omega^2) = 1+ o(a_0^2/\omega^2). \end{align*} On a donc \[\frac{\partial \Phi}{\partial Y} = \sin^2(\omega t) \left [(1-2X)^2 e^{2Y}+2X(1-X)e^Y (e^Y-1) \right ].\] Pour avoir \(\Phi(t,X,0)=0\,\), on doit choisir \[\Phi(t,X,Y)= \sin^2(\omega t) \left [(1-2X)^2 (e^{2Y}-1)/2+X(1-X)(e^Y-1)^2 \right ].\] La fonction génératrice \(F_2(t,x,Y)\) de cette transformation, avec \[\frac{\partial F_2}{\partial Y}=X+o(a_0^2/\omega^2),\quad \frac{\partial F_2}{\partial x}=p+o(a_0^2/\omega^2),\] est donnée par \begin{align*} F_2(t,x,Y)=xY&-\frac{a_0 \varepsilon}{\omega} \sin(\omega t) x(1-x)(e^Y-1) \\ &+ \frac{a_0^2 \varepsilon^2}{2 \omega^2} \sin^2(\omega t) x(1-x)(1-2x)(e^{2Y}-1)\, . \end{align*} Avec \(H(t,x,y)=h(t,X,Y)\,\), le nouveau hamiltonien est \[h(t,X,Y)+\frac{\partial F_2}{\partial t}.\] On a \(T=2\pi/\omega\). En prenant la moyenne de ce hamiltonien, la seconde expression s'annule parce que \[\int_0^T \frac{\partial F_2}{\partial t}\, dt=0\] et il ne reste que le hamiltonien effectif \[\bar{H}(X,Y)=\frac{1}{T} \int_0^T h(t,X,Y)\, dt.\] Un calcul laborieux utilisant le fait que \(\frac{1}{T} \int_0^T \sin^2(\omega t)\, dt=1/2\) conduit à \begin{align*} \bar{H}(X,Y)\simeq &X (1-e^{-Y}) \Bigl [ a_0(1-X)e^Y-b +\frac{ a_0^2 \varepsilon^2}{2\omega^2} \Bigl \{ -a_0 X(1-X)^2 e^{2Y}+\\ & + b(1-X)(1-2X)e^Y - bX(1-X)(e^Y-1)-b(1-2X)^2\Bigr \} \Bigr ]\, . \end{align*} On obtient l'orbite hétérocline perturbée en imposant que le terme entre crochets soit nul. Cette orbite relie \((X^*_\varepsilon,0)\) et \((0,Y^*_\varepsilon)\,\), avec \begin{align*} X^*_\varepsilon &\simeq (1-b/a_0) \left [1-\frac{b(a_0-b)\, \varepsilon^2}{2\omega^2} \right ] ,\quad Y^*_\varepsilon\simeq \log(b/a_0) + \frac{a_0 (a_0-b) \varepsilon^2}{2 \omega^2} . \end{align*} L'action le long de cette orbite hétérocline est \[C=\int_{X_\varepsilon^*}^0 Y\, dX.\] Un autre calcul fastidieux conduit finalement à \begin{equation}\tag{22} C\simeq c_0 - \frac{ (a_0-b)^2 \varepsilon^2}{12\ \omega^2} (1 + 2b/a_0)\, , \end{equation} comme annoncé dans l'introduction. Parce que la fonction \(z\mapsto (1-z)^2(1+2z)\) est inférieure à 1 sur l'intervalle \(0 < z < 1\,\), le terme correctif pour Cest toujours inférieur à \(\frac{a_0^2\, \varepsilon^2}{12\, \omega^2}\,\). C'est petit parce que \(\omega\gg a_0\) par hypothèse. Comme on pouvait s'y attendre, une population sujette à une perturbation haute fréquence dépend peu de l'amplitude de cette perturbation.
Multiplicateurs de Floquet. \(\lambda_1\) peut être estimé directement en calculant les multiplicateurs de Floquet de l'équation maîtresse en utilisant un logiciel tel que Scilab qui résout les équations différentielles ordinaires et calcule les valeurs propres des matrices numériquement. \(e^{\lambda_1 T}\) est la valeur propre avec la deuxième partie réelle la plus grande, la première étant 1. On peut alors tracer \(-\log(-\lambda_1)\) en fonction de N. La pente de cette courbe donne une valeur approchée de C.
Orbite hétérocline. Comme pour (Assaf et coll., 2008), on peut obtenir l'orbite qui relie \((x^*(t),0)\) et \((0,p^*(t))\) par une méthode de tir. On prend la condition initiale \(x^*(0)\) donnée par (15) et une toute petite valeur négative pour \(p(0)\). On varie cette valeur jusqu'à obtenir une solution \((x(t),p(t))\) qui tend à devenir périodique, c'est-à-dire avec \(x(t)\) proche de 0 et \(p(kT)\) proche de \(p^*(0)\) pour k grand (mais pas trop grand pour éviter l'instabilité numérique). On peut alors utiliser l'intégrale (16) pour calculer Cnumériquement.
L'équation aux dérivées partielles. Il est aussi possible de calculer une solution périodique \(S^*(t,x)\) de l'équation de Hamilton-Jacobi (6) en utilisant les méthodes numériques de la théorie des solutions de viscosité. On définit
Méthode de Monte-Carlo. Le temps moyen d'extinction peut aussi être estimé par une méthode de Monte-Carlo. On fait la moyenne des simulations stochastiques. Noter cependant que l'algorithme de Gillespie prenant avantage des temps d'attente distribués exponentiellement ne peut pas être utilisée parce que \(a(t)\) est périodique. Si N croît, le temps d'extinction peut devenir astronomique. On ne présente pas de résultats utilisant cette méthode.
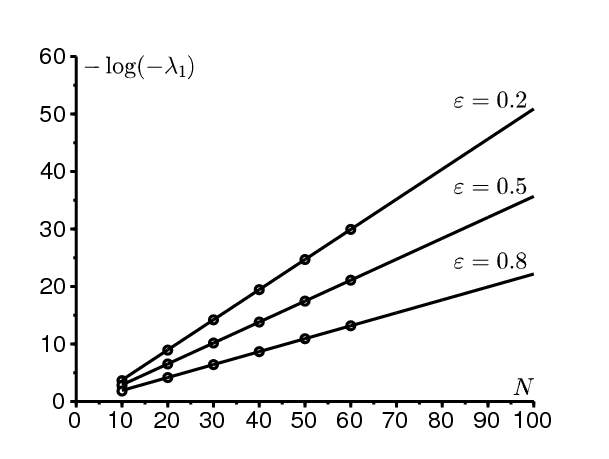
Exemples. On suppose \[a(t)=a_0(1+\varepsilon \cos(2\pi t/T))\] avec \(T=1\) semaine. Considérons d'abord le cas où \(a_0=20\) par semaine et \(b=5\) par semaine. La durée moyenne d'infection est \(1/b= \mbox{1,4}\) jours. On a ainsi \(R_0=a_0/b=4 > 1\) et \(c_0=b/a_0-1-\log(b/a_0)\simeq \mbox{0,636}\). La figure 1 montre \( -\log(-\lambda_1)\) en fonction de N pour \(\varepsilon\in \{0,2\ ;\ 0,5\ ;\ 0,8\}\) et \(N=10\), 20, \(\ldots\), 60, calculé en utilisant les multiplicateurs de Floquet. Les lignes correspondent à une régression linéaire des 3 derniers points \(N=40\), 50, 60. Les pentes de ces lignes, qui sont des estimations de C, sont \(\mbox{0,524}\), \(\mbox{0,364}\) et \(\mbox{0,225}\) pour \(\varepsilon= \mbox{0,2}\), \(\mbox{0,5}\) et \(\mbox{0,8}\).

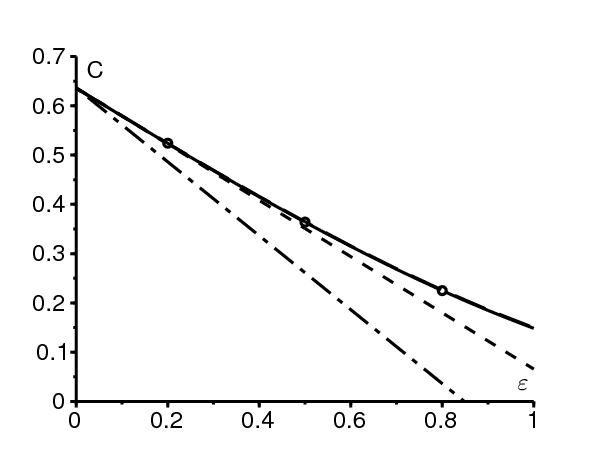
\(a_0\) et \(\omega=2\pi/T\) sont du même ordre de grandeur dans cet exemple. C'est un cas intermédiaire pour la fréquence. On s'attend donc à ce que (19) donne une bonne approximation pour C lorsque ε est petit. La figure 2 montre les courbes suivantes en fonction de ε pour \(0\leq \varepsilon \leq 1\) :
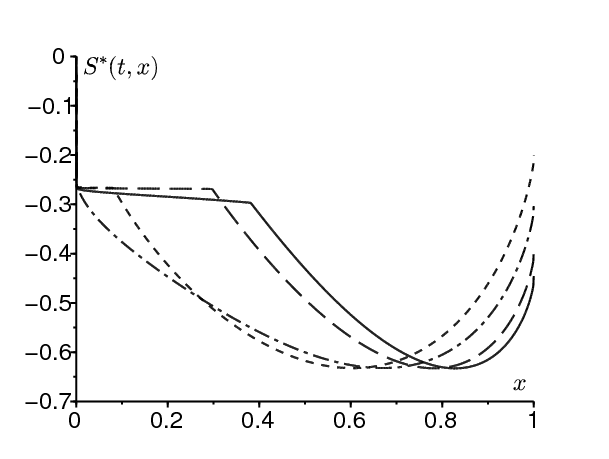
La figure 3 montre une solution périodique \(S^*(t,x)\) de l'équation de Hamilton-Jacobi, tracée en fonction de x pour différentes valeurs de t, lorsque \(\varepsilon= \mbox{0,5}\). Noter la discontinuité de la solution en \(x=0\). Un zoom près de \(x=0\) montrerait que \(S^*(t,0^+)\) est effectivement périodique en temps, de sorte que la condition au bord \(S^*(t,0)=0\) ne peut être satisfaite que dans un sens faible.
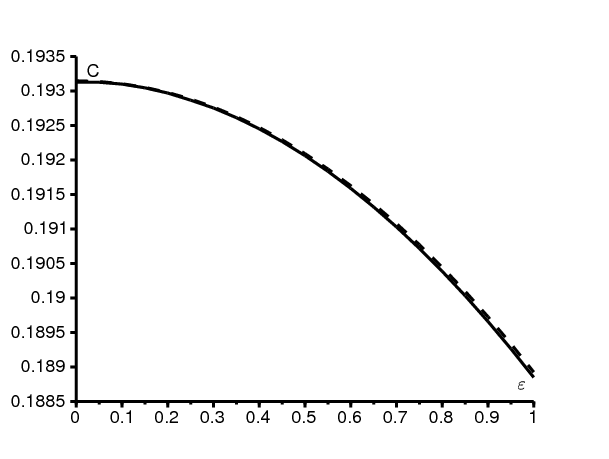
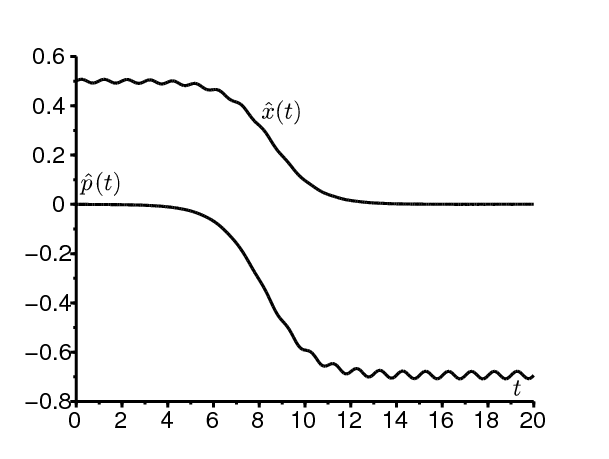
La figure 4 considère un exemple haute fréquence: \(a_0=2\) par semaine et \(b=1\) par semaine. On a ainsi \(R_0=2\) et \(c_0\simeq \mbox{0,1931}\). Dans ce cas \(\omega\simeq \mbox{6,28}\) par semaine est quelque peu supérieur à \(a_0\). Pour \(0\leq \varepsilon \leq 1\,\), on calcule le nombre C en utilisant l'orbite hétérocline et la formule haute fréquence (22). L'accord est bon sur toute la plage de valeurs. Enfin la figure 5 montre l'orbite reliant \((x^*(t),0)\) et \((0,p^*(t))\) pour les mêmes valeurs des paramètres avec \(\varepsilon= \mbox{0,1}\).
Démontrons que \[\int_{-\infty}^{+\infty} \!\!\! e^{\mathrm{i} \lambda u} \frac{e^u}{(1+e^u)^2}\, du = \frac{\pi \lambda}{\sinh (\pi \lambda)}\, .\] D'abord, \(e^u/(1+e^u)^2=1/(4\cosh^2(u/2))\) est une fonction paire. Ceci combiné avec une intégration par parties montre que \begin{align*} \int_{-\infty}^{+\infty} \!\!\! e^{\mathrm{i} \lambda u} \frac{e^u}{(1+e^u)^2}\, du&=2 \int_{0}^{+\infty} \!\!\! \cos(\lambda u) \frac{e^u}{(1+e^u)^2}\, du\\ &=2 \left [\frac{-\cos(\lambda u)}{1+e^u}\right ]_0^\infty - 2 \int_0^\infty \frac{\lambda \sin (\lambda u)}{1+e^u}\, du\\ &= 1 - 2 \lambda \int_0^\infty \frac{e^{-u} \sin (\lambda u)}{1+e^{-u}}\, du\, . \end{align*} En développant en série de puissance \(1/(1+e^{-u})\,\), on obtient \begin{align*} \int_{-\infty}^{+\infty} \!\!\! e^{\mathrm{i} \lambda u} \frac{e^u}{(1+e^u)^2}\, du&=1 - 2 \lambda \sum_{n=0}^\infty (-1)^n \int_0^\infty e^{-(n+1)u} \sin (\lambda u) \, du\\ &=1 + 2 \lambda^2 \sum_{n=0}^\infty \frac{(-1)^{n+1}}{\lambda^2 + (n+1)^2}\, . \end{align*} La somme de cette série peut être calculée avec la formule d'Euler \[\frac{1}{\sin z} = \frac{1}{z} + \sum_{n=1}^\infty (-1)^n \frac{2 z}{z^2-n^2\pi^2}\, ,\] qui est vraie pour tout nombre complexe z avec \(z\neq n\pi\) (n entier). On prend \(z=\mathrm{i} \pi\lambda\). Parce que \(\sin(\mathrm{i}\pi\lambda)=\mathrm{i} \sinh(\pi\lambda)\ \), on obtient \[\frac{\pi \lambda}{\sinh(\pi \lambda)} = 1 + 2\lambda^2 \sum_{n=1}^\infty \frac{(-1)^n}{\lambda^2+n^2}\] et le résultat s'en suit.
Cet article a été stimulé par une discussion avec Hans Metz concernant la taille de population effective dans un environnement périodique lors d'une conférence sur les modèles stochastiques en écologie, évolution et génétique à Angers en décembre 2013.