J. Math. Biol. 75 (2017) 85-108
http://dx.doi.org/10.1007/s00285-016-1079-0
Nicolas Bacaër
Institut de recherche pour le développement
Les Cordeliers, Paris, France
nicolas.bacaer@ird.fr
On obtient une formule explicite pour le taux d'extinction des processus linéaires de naissance et de mort sous-critiques dans un environnement aléatoire. On illustre cette formule en calculant numériquement la valeur propre de plus grande partie réelle pour la matrice tronquée de l'équation maîtresse. La fonction génératrice du vecteur propre associé vérifie un système singulier d'équations différentielles du type de Fuchs. Une attention particulière est portée au cas de deux environnements, qui conduit à une équation différentielle de Riemann.
Supposons que l'environnement oscille entre un nombre fini K d'états (\(K\geq 2\)) suivant une chaîne de Markov en temps continu homogène. \(Q=(Q_{i,j})\) est la matrice dont la transposée est le générateur infinitésimal de cette chaîne: \[Q_{i,j}\geq 0 \quad \forall i\neq j, \quad \sum_{i} Q_{i,j}=0 \quad \forall j.\] On suppose que la matrice Q est irréductible. Il existe un unique vecteur \(u=(u_i)\) avec \[Qu=0, \quad \sum_{i} u_i=1\] (Sericola, 2013, p. 152).
Le nombre d'individus qui évoluent dans cet environnement aléatoire est n. Dans l'environnement i (\(1\leq i \leq K\)), supposons qu'on ait un processus linéaire de naissance et de mort de paramètres
Supposons qu'au temps t=0 il y ait \(\,n_0\) individus (\(n_0\geq 1\)) et que l'environnement soit \(i_0\). La probabilité d'avoir n individus dans l'environnement i au temps t est \(\,p_{n,i}(t)\). On a donc \(\,p_{n,i}(0)=1\) si \((n,i)=(n_0,i_0)\) et \(p_{n,i}(0)=0\,\) sinon. L'équation maîtresse est \begin{equation} \frac{dp_{n,i}}{dt} = a_i (n-1) p_{n-1,i} + b_i(n+1) p_{n+1,i} -(a_i + b_i) n \, p_{n,i}+\sum_{j} Q_{i,j} p_{n,j}, \quad n\geq 0,\quad 1\leq i \leq K. \tag{1} \end{equation} Mais \(p_{n-1,i}\) est absent pour \(n=0\). Comme (Lotka, 1939), définissons \[R_0=\frac{\sum_{i=1}^K a_i\, u_i}{\sum_{i=1}^K b_i\, u_i}\, .\] On supposera toujours que \(R_0 < 1\) : la population va vers l'extinction presque sûrement (Cogburn et Torrez, 1981 ; Bacaër et Ed-Darraz, 2014). C'est le régime sous-critique. Avec \(\,t\to +\infty\,\), on a \[p_{0,i}(t)\to u_i,\quad p_{n,i}(t)\to 0, \quad \forall n\geq 1, \quad \forall i.\] Le taux d'extinction existe et ne dépend pas de n≥ 1 ou de i \begin{equation} \omega_1=\lim_{t\to +\infty} \frac{1}{t} \log p_{n,i}(t) \tag{2} \end{equation} (Collet et coll., 2013, section 4.5). Il ne dépend pas non plus de la condition initiale \(\,(n_0,i_0)\). Le problème est de déterminer explicitement ce taux.
On utilise quelques notations :
Dans la section 2, on utilise un résultat de (D'Souza et Hambly, 1997) concernant les processus de branchement en environnement aléatoire pour montrer que \begin{equation} \omega_1 = \Lambda\, :=\, \min_{0\leq \alpha\leq 1} s(Q+\alpha D)\, . \tag{3} \end{equation} On étudie aussi les variations de la fonction \(\alpha \mapsto \lambda_1(\alpha)=s(Q+\alpha D)\) et de la dérivée \(\lambda_1'(\alpha)\), ce qui conduit à distinguer trois cas:
Dans la section 3, on observe que la borne spectrale \(\mu_N\,\) de la matrice tronquée de l'équation maîtresse forme une suite croissante. Puis on calcule numériquement \(\,\mu_N\,\) dans une série d'exemples. On remarque en particulier la lenteur, sans doute logarithmique, avec laquelle \(\,\mu_N\) converge vers \(\omega_1\) dans le troisième cas évoqué ci-dessus.
À partir de la section 4, on s'intéresse aux autres valeurs propres et aux vecteurs propres associés, pour lesquels on n'obtient que des résultats très partiels. On transforme d'abord le problème de valeur propre \begin{equation} \omega\, \pi_{n,i} = a_i (n-1) \pi_{n-1,i} + b_i(n+1) \pi_{n+1,i} -(a_i + b_i) n \, \pi_{n,i} +\sum_{j} Q_{i,j} \pi_{n,j}\, , \tag{4} \end{equation} en un système différentiel singulier du type de Fuchs (Methée, 1959) \begin{equation} \omega\, G_i(x)+(1-x)(a_i x-b_i) G_i'(x) = \sum_j Q_{i,j} G_j(x) \tag{5} \end{equation} pour la fonction génératrice \begin{equation} G_i(x)=\sum_{n\geq 0} \pi_{n,i}\, x^n\, . \tag{6} \end{equation} Si le vecteur propre \((\pi_{n,i})\) décroît géométriquement par rapport à n, alors la valeur propre ω est nécessairement égale à la valeur propre d'une matrice \(\,Q+\nu D\) avec ν entier \(\geq 0\). Si m<0 et \(\,\omega=s(Q+\nu D)\,\), on construit effectivement des solutions analytiques du système (5) au voisinage de x=1. L'équation caractéristique du système fuchsien est \begin{equation} \mathrm{det}(Q+\alpha D-\omega I)=0\, ; \tag{7} \end{equation} autrement dit, \(\omega\) est une valeur propre de la matrice \(Q+\alpha D\). On obtient cette équation caractéristique en cherchant des solutions qui se comportent comme \((1-x)^\alpha\) au voisinage de \(x=1\).
Étudions le troisième cas : la fonction \(\lambda_1(\alpha)\, \) atteint son minimum à l'intérieur de \(]0,1[\). Si on suppose
Dans la section 5, on étudie directement le comportement asymptotique du vecteur propre limite \(\pi=(\pi_{n,i})\) associé à \(\omega_1\). La section 6 fait le lien lorsque K=2 avec une équation différentielle de Riemann. Dans la section 7, on s'intéresse à la chaîne de Markov incluse, cette dernière rentrant dans le cadre des travaux de (Dekking, 1988) et de (Geiger et coll., 2003). On remarque que le seuil entre les régimes faiblement et fortement sous-critiques n'est pas le même que celui où \(\Lambda \neq s(Q+D)\).
Pour mieux situer notre problème par rapport à quelques autres travaux, on note que le système (1) est un « processus non homogène de quasi naissance et de mort »; voir par exemple (Sericola, 2013, p. 350) ou (Latouche et Ramaswami, 1999, chapitre 12), qui discutent de la distribution stationnaire mais pas du taux de convergence vers celle-ci. Par ailleurs, dans un environnement constant avec \[a_i=a, \quad b_i=b > a, \quad \forall i,\] on a \(D=(a-b)I\,\) et \(\,I\,\) est la matrice identité. On a donc \(\,s(Q+\alpha D)=\alpha (a-b)\) et la formule (3) donne \(\omega_1=a-b\). Ceci est bien connu soit par un calcul direct (Hillion, 1986, chapitre V), soit comme cas particulier des résultats de Karlin et McGregor sur les processus de naissance et de mort (Collet et coll., 2013, section 5.9.2). Les généralisations de ces derniers résultats aux « quasi processus de naissance et de mort » (Clayton, 2010) ne concernent que des cas où le « spectre » est réel. Ce n'est pas le cas en général dans notre modèle. Enfin, le modèle (1) intervient comme linéarisation de certains modèles de population non linéaires, et notamment de modèles épidémiques (Bacaër, 2016).
\(\,M^\mathsf{T}\) est la transposée d'une matrice M (ou d'un vecteur). On choisit un petit pas de temps \(\,\delta > 0\). La matrice \[\,\mathcal{P}=e^{Q^\mathsf{T} \delta}\,\] est la matrice d'une chaîne de Markov en temps discret. On a \(\,\mathcal{P}_{i,j} > 0\ \forall i,\, \forall j,\,\) parce que la matrice Q est irréductible. L'environnement reste bloqué dans l'état i pendant un pas de temps δ. Puis l'environnement saute à l'état j, avec une probabilité \(\mathcal{P}_{i,j}\). Dans l'intervalle de temps de longueur δ, la population suit un processus linéaire de naissance et de mort de paramètres \(\,n\, a_i\) et \(n\, b_i\,\) si l'environnement est dans l'état i. Ainsi, un individu génère en moyenne \[\,m_i=e^{(a_i-b_i)\delta}\,\] individus. On a \(0 < m_i < +\infty\). On se trouve donc dans le cadre d'un processus de branchement en environnement markovien. Quelques notations :
On définit \begin{equation} \lambda_1(\alpha)=s(Q+\alpha D),\quad \Lambda=\min_{0\leq \alpha \leq 1} \lambda_1(\alpha),\quad m=\max_{1\leq i\leq K} (a_i-b_i)=\max_i d_i\, . \tag{11} \end{equation}
Proposition 1.
Preuve. Si v=\((v_i)\) est un vecteur,
Reprenons le raisonnement de la section 9 de (Bacaër, 2016) mais avec \(R_0 < 1\) au lieu de \(R_0 > 1\). La matrice \(\,Q+\alpha D\,\) est irréductible pour tout α parce que la matrice Q est irréductible et la matrice D diagonale. Ainsi \(\lambda_1(\alpha)\) est une valeur propre simple de la matrice \(Q+\alpha D\), \[\exists !\ w_1(\alpha)\gg 0,\quad (Q+\alpha D)\, w_1(\alpha) = \lambda_1(\alpha) \, w_1(\alpha),\quad \langle \mathbf{1}^\mathsf{T},w_1(\alpha)\rangle =1.\] \(\mathbf{1}=(1,\ldots,1)\) et \(\langle \cdot,\cdot \rangle\,\) désigne le produit scalaire usuel de vecteurs réels. \(\lambda_1(\alpha)\) est aussi une valeur propre simple de la matrice transposée \(Q^\mathsf{T}+\alpha D\), \[\exists !\ v_1(\alpha)\gg 0,\quad (Q^\mathsf{T}+\alpha D)\, v_1(\alpha) = \lambda_1(\alpha)\, v_1(\alpha),\quad \langle v_1(\alpha),w_1(\alpha) \rangle=1.\] D'après le théorème de perturbation des valeurs propres simples, on sait que la fonction \(\lambda_1(\alpha)\) est dérivable et \begin{equation} \lambda_1'(\alpha)=\langle v_1(\alpha),D\, w_1(\alpha)\rangle\, .\tag{12} \end{equation} En particulier pour \(\alpha=0\,\), on a \(\lambda_1(0)=s(Q)=0\), \(w_1(0)=u\), \(v_1(0)=\mathbf{1}^\mathsf{T}\) et \[\lambda_1'(0)=\langle \mathbf{1}^\mathsf{T},D\, u\rangle =\sum_{i=1}^K (a_i-b_i)u_i < 0\] parce que \(R_0 < 1\).
Si m≤0, la fonction \(\alpha \mapsto \lambda_1(\alpha)\) est décroissante parce que \(D\leq 0\). Considérons maintenant le cas où \(\,m > 0\). On a \(\,\lambda_1'(0) < 0\). La fonction \(\,\alpha\mapsto \lambda_1(\alpha)\,\) est convexe (Cohen, 1981). Donc \(\,\alpha \mapsto \lambda_1'(\alpha)\,\) est une fonction croissante. Par ailleurs, si \(\,\alpha \to +\infty\,\), on a \(\lambda_1(\alpha) \sim \alpha\, m \to +\infty\). La fonction \(\,\alpha\mapsto \lambda_1(\alpha)\,\) est dans ce cas strictement convexe puisqu'elle n'est pas affine (Nussbaum, 1986). Il existe donc un unique \(\,\alpha^* > 0\) avec \(\lambda_1'(\alpha^*)=0\).
Ainsi donc, trois cas se présentent:
On suppose \(K=2\). Avec \(\,Q_{i,i}=-q_i\) si \(i=1,2\,\), on a \[Q=\left (\begin{array}{cc} -q_1 & q_2 \\ q_1 & -q_2 \end{array}\right ),\quad u_1=\frac{q_2}{q_1+q_2}\, ,\quad u_2=\frac{q_1}{q_1+q_2}\, .\] L'équation caractéristique det}(Q+\alpha D - \omega I)=0\) s'écrit \[\omega^2-(-q_1+\alpha d_1 -q_2 +\alpha d_2) \omega + (-q_1+\alpha d_1)(-q_2+\alpha d_2)-q_1 q_2=0\, .\] Cette relation entre \(\omega\) et \(\alpha\) décrit une hyperbole dans le plan \((\omega,\alpha)\). Elle peut aussi s'écrire \begin{equation} \alpha^2 -\alpha \left (\frac{\omega+q_1}{d_1}+\frac{\omega+q_2}{d_2}\right )+\frac{(\omega+q_1)(\omega+q_2)-q_1 q_2}{d_1 d_2}=0. \tag{13} \end{equation} De plus, \(\lambda_1(\alpha)=s(Q+\alpha D)\) est tel que \[2\, \lambda_1(\alpha)=-q_1-q_2+\alpha(d_1+d_2)+\sqrt{[\alpha(d_1-d_2)+q_2-q_1]^2+4q_1 q_2}\, \] et \[2\, \lambda_1'(1)=d_1+d_2+\frac{(d_1-d_2)(d_1-d_2+q_2-q_1)}{\sqrt{(d_1-d_2+q_2-q_1)^2+4q_1 q_2}}\, .\] Si m≤0, ou si m>0 et \(\,\lambda_1'(1)\leq 0\,\), on a \(\Lambda =\lambda_1(1)\). Si m>0 et \(\,\lambda_1'(1) > 0\,\), on a forcément \(d_1d_2 < 0\). Supposons dans ce cas par exemple que \(\,d_1 > 0\) et \(d_2 < 0\). En annulant le discriminant de (13), on trouve après un petit calcul que \begin{equation} \Lambda = -\frac{\left (\sqrt{-q_1 d_2}-\sqrt{q_2 d_1}\right )^2}{d_1-d_2} \, ,\quad \alpha^*=\frac{1}{2}\left [\frac{\Lambda+q_1}{d_1}+\frac{\Lambda+q_2}{d_2} \right ] . \tag{14} \end{equation} Remarquer que \(\Lambda=0\) et \(\alpha^*=0\) si \(q_1d_2+q_2d_1=0\), c'est-à-dire si \(R_0=1\).
Avec \(\,p=(p_{0,1},\ldots,p_{0,K},\ldots,p_{n,1},\ldots,p_{n,K},\ldots)^\mathsf{T}\,\), l'équation maîtresse s'écrit \(\frac{dp}{dt}=\mathcal{M}p\). \(\,\mathcal{M}\,\) est une matrice infinie. Tronquons la matrice \(\,\mathcal{M}\,\) \[\mathcal{M}^{(N)}= \left (\begin{array}{cccccc} Q & B & 0 & 0 &\cdots & 0\\ 0 & Q-S & 2B & 0&\cdots& 0\\ 0 & A & Q-2S & 3B& & 0\\ 0 & 0 & 2A & Q-3S& & 0\\ \vdots & \vdots &\ddots && \ddots& \\ 0 &0 &0&0 & &Q-NS \end{array} \right )=\left ( \begin{array}{c|c} Q & \ast \\ \hline 0 & \, \mathcal{U}^{(N)} \end{array}\right )\] avec \(S=A+B\). On définit \(\,\mu_N=s(\mathcal{U}^{(N)})\).
Proposition 2. Pour tout entier \(\,N\geq 1\,\), on a \(\mu_N < \mu_{N+1} < 0\). \(\,(\mu_N)\) a donc une limite si \(N\to +\infty\,\), qui est \(\omega_1\).
Preuve. Une matrice de Metzler est une matrice dont tous les coefficients hors diagonale sont ≥ 0. La matrice \(\,\mathcal{U}^{(N)}\,\) est une matrice de Metzler irréductible parce que Q est irréductible, \(\,a_i > 0\) et \(b_i > 0\ \forall i\). On peut donc utiliser les corollaires du théorème de Perron et Frobenius concernant la borne spectrale des matrices de Metzler; voir par exemple (Nkague Nkamba, 2012, théorème 30). Avec \(\,e=(1,\ldots,1)^\mathsf{T}\,\) on a \[(\mathcal{U}^{(N)})^\mathsf{T}e=(-b_1,\ldots,-b_K,0,\ldots,0,-Na_1,\ldots,-Na_K) < 0=0\cdot e.\] Parce que \(e\gg 0\,\), on en déduit que \(s((\mathcal{U}^{(N)})^\mathsf{T}) < 0\). On a donc \[\mu_N=s(\mathcal{U}^{(N)}) =s((\mathcal{U}^{(N)})^\mathsf{T}) < 0.\]
\(\mu_N\) est une valeur propre de la matrice \(\mathcal{U}^{(N)}\) \[\exists\, \mathcal{W}^{(N)}\gg 0,\quad \mathcal{U}^{(N)}\mathcal{W}^{(N)}=\mu_N \, \mathcal{W}^{(N)}.\] Le vecteur \(\,\mathcal{W}^{(N)}\,\) est composé de N blocs de taille K, \(\mathcal{W}^{(N)}=(\mathcal{W}^{(N)}_1,\ldots,\mathcal{W}^{(N)}_N)\). Considérons le vecteur \[\,\widetilde{\mathcal{W}}=(\mathcal{W}^{(N)},\, 0)\] 0 est aussi de taille K. On a alors \[\mathcal{U}^{(N+1)}\widetilde{\mathcal{W}}=\left (\begin{array}{ccc|c} & & & \vdots\\ &\mathcal{U}^{(N)} & &0\\ & & &(N+1)B\\ \hline \cdots &0& NA &Q-(N+1)S \end{array}\right ) \left ( \begin{array}{c} \\ \mathcal{W}^{(N)}\\ \\ \hline 0 \end{array}\right )=\left (\begin{array}{c} \\ \mu_N \, \mathcal{W}^{(N)}\\ \\ \hline NA\, \mathcal{W}^{(N)}_N \end{array}\right ). \] Parce que \(NA\, \mathcal{W}^{(N)}_N\gg 0\,\), on a \(\,\mathcal{U}^{(N+1)}\widetilde{\mathcal{W}} > \mu_N \widetilde{\mathcal{W}}\). Parce que \(\widetilde{\mathcal{W}} > 0\,\), on en déduit que \(\mu_{N+1} > \mu_N\).
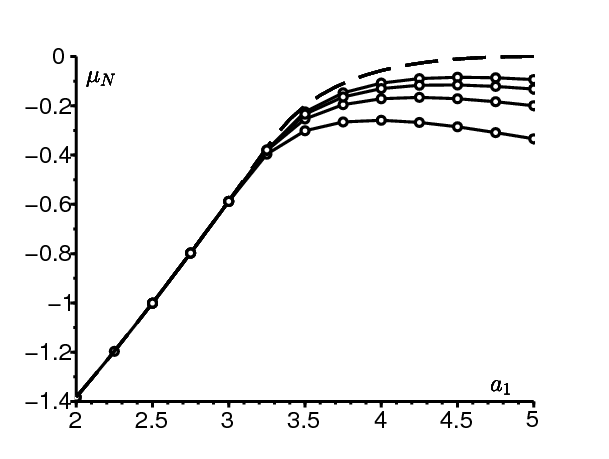
Comme valeurs numériques, prenons \begin{equation} q_1=q_2=1,\quad a_2=1,\quad b_1=b_2=3\, . \tag{15} \end{equation} On a alors \(u_1=u_2= \mbox{0,5}\). Le paramètre \(a_1\) varie par exemple entre 2 et 5; cette limite supérieure correspond à \(\,R_0=1\). Pour des petites valeurs de N, typiquement jusqu'à \(\,N=10^3\ \), un logiciel tel que Scilab calcule le spectre complet de la matrice \(\mathcal{U}^{(N)}\,\). Sinon on calcule la plus petite valeur propre de \(\,-\mathcal{U}^{(N)}\) et le vecteur propre correspondant par une méthode itérative appliquée à la matrice inverse. On tire avantage de la structure tridiagonale par bloc pour l'inversion à chaque itération (Artalejo et coll., 2013). Avec cet algorithme, on peut aller jusqu'à \(\,N=10^6\) sans trop de problèmes.
La figure 1 montre \(\mu_N\) en fonction de \(a_1\) pour N fixé mais grand. L'algorithme itératif est arrêté lorsque deux estimations consécutives de \(\,\mu_N\) diffèrent de moins que \(10^{-4}\). La figure montre aussi en pointillé et en fonction de \(\,a_1\) le nombre Λ donné par la formule (3), qui vaut \(\lambda_1(1)\) si \(\lambda_1'(1)\leq 0\) et qui est donné par la formule (14) lorsque \(\lambda_1'(1) > 0\). On a \(\,\lambda_1'(1) < 0\) si \(a_1 < a_1^*\) et \(\lambda_1'(1) > 0\) si \(a_1 > a_1^*\ \), avec \(a_1^*\simeq \mbox{3,2829}\). L'accord entre Λ et la limite des \(\,(\mu_N)\) semble probable. Néanmoins, la convergence est extrêmement lente, peut-être logarithmique, lorsque \(\,R_0\) se rapproche de 1, en particulier lorsque \(a_1 > a_1^*\).

On s'intéresse désormais à la limite \(N\to \infty\) du vecteur propre associé à \(\mu_N\,\) ainsi qu'aux autres valeurs et vecteurs propres. À ce sujet, on n'obtiendra que des résultats très partiels.
\(\mathbb{K}=\{1,2,\ldots,K\}\), \(\mathbb{N}=\{0,1,2,\ldots\}\), \(\mathbb{C}\) est l'ensemble des nombres complexes et \('\) la dérivée par rapport à la variable \(x\).
Proposition 3.
\(G_i(x)\) est solution du système (5) pour \(x\in \mathbb{C}\), \(|x| < R\) et \(1\leq i\leq K\).
Preuve. On a \[G_i'(x)=\sum_{n\geq 1} n\, \pi_{n,i}\, x^{n-1},\quad \forall |x| < R.\] Comme dans le cas classique avec environnement constant (Hillion, 1986), on multiplie (4) par \(\,x^n\). La sommation sur tous les n≥ 0 donne \[\omega\, G_i(x) = a_i \, x^2\, G'_i(x) + b_i\, G'_i(x) -(a_i + b_i) x\, G'_i(x) +\sum_{j} Q_{i,j} G_j(x).\] Ceci équivaut à (5).
Remarques.
Proposition 4.
Preuve. Raisonnons par l'absurde. Supposons que pour tout ν≥0, ω ne soit pas une valeur propre de \(\,Q+\nu D\). Les fonctions \(\,G_i(x)\) sont analytiques dans un disque \(|x| < R\) avec \(R > 1\). Si x converge vers 1 dans (5) : \[\omega \, G_i(1)=\sum_j Q_{i,j}\, G_j(1)\, .\] Mais ω n'est pas une valeur propre de Q. Donc \(G_i(1)=0\ \forall i\).
Soit un entier \(\nu\geq 1\). Par récurrence, supposons que l'on ait prouvé \(\,G_i^{(\nu-1)}(1)=0\). On dérive ν fois l'équation (5) par rapport à x et on utilise la formule de Leibniz pour le produit de \(\,(1-x)(a_ix-b_i)\) et \(G_i'(x)\). On a \[\omega\, G_i^{(\nu)}(x)+\sum_{k=0}^\nu \binom{\nu}{k} [(1-x)(a_ix-b_i)]^{(k)} G_i^{(\nu-k+1)}(x)=\sum_j Q_{i,j}\, G_j^{(\nu)}(x)\, .\] \(\binom{\nu}{k}\,\) désigne le coefficient du binôme. Le polynôme \(\,(1-x)(a_ix-b_i)\,\) est de degré 2 en x. Seuls les expressions avec \(\,0\leq k\leq 2\) sont non nuls dans la somme de gauche: \begin{align*} \omega\, G_i&^{(\nu)}(x)+(1-x)(a_ix-b_i)G_i^{(\nu+1)}(x) \\ &+\nu [a_i(1-2x)+b_i]G_i^{(\nu)}(x)-a_i \nu (\nu-1) G_i^{(\nu-1)}(x)=\sum_j Q_{i,j}\, G_j^{(\nu)}(x)\, . \end{align*} On fait converger x vers 1 et on trouve avec l'hypothèse de récurrence \[\omega G_i^{(\nu)}(1) - \nu (a_i-b_i) G_i^{(\nu)}(1)=\sum_j Q_{i,j} G_j^{(\nu)}(1)\, .\] Cependant ω n'est pas une valeur propre de la matrice \(\,Q+\nu D\). Donc \(\,G_i^{(\nu)}(1)=0\ \forall i\).
Ainsi, on a démontré que \(G_i^{(\nu)}(1)=0\ \forall i\) et pour tout nombre entier ν≥0. Parce que la fonction \(\,G_i(x)\) est analytique, on a \(G_i(x)=0\) dans un voisinage de \(x=1\,\), et même \(G_i(x)=0\) dans tout le disque \(|x| < R\ \) d'après le principe du prolongement analytique. On a donc \(\,\pi_{n,i}=G_i^{(n)}(0)/n!=0\ \forall n\geq 0\) et \(1\leq i\leq K\). Ceci contredit l'hypothèse \(\,\pi \neq 0\).
Remarques.
Exemple. Reprenons les valeurs numériques (15) avec \(a_1= \mbox{2,5}\). Dans ce cas, on a \(\,m < 0\). Pour \(N=1000\), les vingt premières valeurs propres de la matrice \(\mathcal{M}^{(N)}\) sont à peu près données par le tableau suivant:
\[ \begin{array}{lllll} 0& -1& -\mbox{1,6972244}& -2& -\mbox{2,2877855}\\ -\mbox{2,8377223} & -\mbox{3,3689563} & -\mbox{3,5} & -\mbox{3,8902278} & -\mbox{4,4056104}\\ -\mbox{4,9172375}& -\mbox{5,3027756} & -\mbox{5,426328} & -\mbox{5,933627}& -\mbox{6,4396149}\\ -\mbox{6,9446154} & -\mbox{7,2122145}& -\mbox{7,448851}& -\mbox{7,9524836}& -\mbox{8,4556214}. \end{array} \]
Or les valeurs propres de \(Q\) sont 0 et \(-2\), celles de \(Q+D\) sont \(-1\) et \(-\mbox{3,5}\), celles de \(Q+2D\) sont \(-\mbox{1,6972244}\) et \(-\mbox{5,3027756}\), celles de \(Q+3D\) sont \(-\mbox{2,2877855}\) et \(-\mbox{7,2122145}\), celles de \(Q+4D\) sont \(-\mbox{2,8377223}\) et \(-\mbox{9,1622777}\,\), etc. On les retrouve dans le tableau ci-dessus. Il semble donc que les valeurs propres de \(\,\mathcal{M}^{(N)}\) convergent quand \(N\to +\infty\) vers les valeurs propres des matrices \(Q+\nu D\) pour \(\nu=0,1,2\ldots\) et \(\mu_N\) converge vers \(s(Q+D)\). Rappelons qu'ici \(\,s(Q+D)=\Lambda\) parce que \(m < 0\).
On suppose \(m < 0\). Cherchons formellement une solution au voisinage de x=1 du système (5) de la forme \begin{equation} \sum_{n=0}^\infty c_{n,i} (1-x)^n\, . \tag{17} \end{equation} On a \[ \omega \sum_{n=0}^\infty c_{n,i} (1-x)^n - (a_i x-b_i)\sum_{n=0}^\infty n\, c_{n,i} (1-x)^n =\sum_j Q_{i,j} \sum_{n=0}^\infty c_{n,j} (1-x)^n. \] On a \(a_ix-b_i=a_i-b_i-a_i(1-x)\,\). On identifie les coefficients de \(\,(1-x)^n\). On obtient \[[\omega -(a_i-b_i)n]c_{n,i}+a_i(n-1)c_{n-1,i}=\sum_j Q_{i,j} c_{n,j},\quad \forall n\geq 0.\] \(c_{n-1,i}\) est absent si \(n=0\). Avec \(\,c_n=(c_{n,1},\ldots,c_{n,K})\), (17) est une solution de (5) si \begin{equation} [Q-\omega I]c_0=0\, ,\quad [Q+nD-\omega I]c_n = (n-1)Ac_{n-1} \, ,\quad n\geq 1. \tag{18} \end{equation}
Un premier type de solution s'obtient en choisissant \(\omega\) parmi les valeurs propres de \(Q\) et \(c_0\,\) un vecteur propre correspondant. La relation (18) permet de calculer \(\,c_n\) pour \(n\geq 1\), pourvu que la matrice \(Q+nD-\omega I\) soit toujours inversible.
Un deuxième type de solution s'obtient en choisissant \(c_0=c_1=\cdots=c_{\nu-1}=0\) avec \(\nu\geq 1\), \(\omega\) une valeur propre de \(Q+\nu D\) et \(c_\nu\,\) un vecteur propre associé. Puis on calcule \(\,c_n\) pour \(n\geq \nu+1\) avec l'équation (18), pourvu encore que la matrice \(Q+nD-\omega I\) soit toujours inversible.
Prenons en particulier \(\omega=s(Q+\nu D)\) avec un nombre entier \(\,\nu\geq 0\). Parce que \(\,a_i < b_i\ \forall i\), on a \(D < 0\). De plus, \(\,Q+\nu D\ \) est irréductible. Donc pour tout nombre entier n>ν, on a \[s(Q+nD) < s(Q+\nu D)=\omega.\] On a donc \(\,s(Q+nD-\omega I) < 0\). La matrice \(\,Q+nD-\omega I\) est une matrice de Metzler inversible et \((Q+nD-\omega I)^{-1}\ll 0\). On a \[c_n=[Q+nD-\omega I]^{-1}(n-1)Ac_{n-1},\quad \forall n\geq 1.\] Avec \(\,n\to +\infty\), \[[Q+nD-\omega I]^{-1}(n-1)A\to D^{-1}A\] et \[\,c_{n,i}/c_{n-1,i}\to a_i/(a_i-b_i).\] La série (17) est convergente pour \(\,|1-x| < |\frac{b_i}{a_i}-1|\). Les séries (17) pour \(\,1\leq i \leq K\) sont toutes convergentes pour \(|1-x| < \min_i |\frac{b_i}{a_i}-1|\).
Dans les deux sections précédentes, il était question des valeurs propres des matrices Q+ν D pour un nombre entier ν ≥ 0. Cependant (Bacaër et Ed-Darraz, 2014) ont déjà mis en évidence un exemple où \(\,R_0 < 1\) mais où la valeur propre \(s(Q+D)\) de la matrice \(Q+D\) est strictement positive: il suffit de prendre \(q_1=q_2=1\), \(a_1= \mbox{2,7}\), \(a_2= \mbox{0,8}\), \(b_1=b_2=2\) (donc \(a_1 > b_1\)). Or notre problème initial ne peut avoir de valeur propre positive. On en conclut en particulier que les séries génératrices \(\,G_i(x)\) n'ont pas toujours un rayon de convergence \( > 1\). La proposition suivante lie le comportement de \(\,G_i(x)\) près de \(x=1\) avec le paramètre \(\alpha\).
Proposition 5.
Preuve. On a \begin{align*} G'_i(x)=& (1-x)^\alpha \sum_{j=0}^J \bigl [\log(1-x)\bigr ]^j g_{i,j}'(x)\\ &+(1-x)^{\alpha-1} \sum_{j=0}^J \Bigl \{-\alpha \bigl [\log(1-x)\bigr ]^j - j \bigl [\log(1-x)\bigr ]^{j-1}\Bigr \} g_{i,j}(x)\, . \end{align*} \(G_i(x)\) est solution de l'équation (5) pour \(|x| < 1\). On divise par \(\,(1-x)^\alpha \bigl [\log(1-x)\bigr ]^J\). On a \begin{align*} &\omega \sum_{j=0}^J \bigl [\log(1-x)\bigr ]^{j-J} g_{i,j}(x) +(1-x)(a_ix-b_i) \sum_{j=0}^J \bigl [\log(1-x)\bigr ]^{j-J} g_{i,j}'(x)\\ & +(a_i x-b_i) \sum_{j=0}^J \Bigl \{-\alpha \bigl [\log(1-x)\bigr ]^{j-J} - j \bigl [\log(1-x)\bigr ]^{j-1-J}\Bigr \} g_{i,j}(x)\\ &=\sum_j Q_{i,j} \sum_{h=0}^J \bigl [\log(1-x)\bigr ]^{h-J} g_{j,h}(x) \, . \end{align*} Avec \(x\to 1\,\), on obtient \[\omega g_{i,J}(1)-\alpha (a_i-b_i)g_{i,J}(1) = \sum_j Q_{i,j} g_{j,J}(1)\, . \] Donc ω est une valeur propre de la matrice \(Q+\alpha D\).
Remarque. La forme de la fonction \(\,G_i(x)\) dans la proposition 5, qui combine fonction puissance et un polynôme en logarithme, est celle que l'on peut attendre d'une solution d'un système de Fuchs au voisinage d'une singularité (Gantmacher, 1966, p. 159).
Proposition 6.
On suppose : \(\,m > 0\) et \(\lambda_1'(1) > 0\). Dans ce cas, \(\Lambda=\lambda_1(\alpha^*)\) avec \(\alpha^*\in ]0,1[\). On suppose : α > 0 et \(\,\omega=s(Q+\alpha D)\).
alors α=\(\alpha^*\) et ω=Λ.
Preuve. En effet, \[G_i'(x)=-\sum_{j=0}^J \sum_{n=0}^\infty g_{i,j,n} \bigl [ j+(n+\alpha) \log(1-x) \bigr ] \bigl [ \log(1-x) \bigr ]^{j-1} (1-x)^{n+\alpha-1} \, . \] On a \(a_ix-b_i=a_i-b_i-a_i(1-x)\). Parce que \(\,G_i(x)\) est une solution de (5) sur \(|x| < 1\,\), on a \begin{align*} &\omega \sum_{j=0}^J \sum_{n=0}^\infty g_{i,j,n} \bigl [ \log(1-x) \bigr ]^j (1-x)^{n+\alpha}\\ & -(a_i-b_i) \sum_{j=0}^J \sum_{n=0}^\infty g_{i,j,n} \bigl [ j+(n+\alpha) \log(1-x) \bigr ] \bigl [ \log(1-x) \bigr ]^{j-1} (1-x)^{n+\alpha}\\ &+a_i \sum_{j=0}^J \sum_{n=0}^\infty g_{i,j,n} \bigl [ j+(n+\alpha) \log(1-x) \bigr ] \bigl [ \log(1-x) \bigr ]^{j-1} (1-x)^{n+\alpha+1}\\ &=\sum_{k=1}^K Q_{i,k} \sum_{j=0}^J \sum_{n=0}^\infty g_{k,j,n} \bigl [ \log(1-x) \bigr ]^j (1-x)^{n+\alpha}\, . \end{align*} Les expressions en \((1-x)^\alpha [\log(1-x)]^J\) et en \((1-x)^\alpha [\log(1-x)]^{J-1}\) doivent chacunes s'annuler: \begin{align*} \omega g_{i,J,0} -\alpha(a_i-b_i)g_{i,J,0}&=\sum_k Q_{i,k} \, g_{k,J,0}\ ,\\ \omega g_{i,J-1,0} -(a_i-b_i) \bigl [J g_{i,J,0}+\alpha g_{i,J-1,0}\bigr ]&=\sum_k Q_{i,k} g_{k,J-1,0}\ . \end{align*} On définit \(\gamma_j=(g_{i,j,0})_{1\leq i \leq K}\,\). On a \[ (Q+\alpha D-\omega I)\gamma_J=0\, ,\quad (Q+\alpha D-\omega I) \gamma_{J-1}+J D \gamma_J=0\, . \] Parce que \(\omega=s(Q+\alpha D)\) et \(\gamma_J\neq 0\,\), la première équation montre que \(\gamma_J\) est un vecteur propre de la matrice \(Q+\alpha D\) associé à la valeur propre \(s(Q+\alpha D)\). Avec les notations de la section 2.2, on en déduit qu'il existe une constante \(\,\kappa \neq 0\) avec \(\gamma_J=\kappa\, w_1(\alpha)\). De plus, on voit que la deuxième équation prend la forme \begin{equation} [Q+\alpha D-\lambda_1(\alpha) I]\gamma_{J-1}+J \kappa\, Dw_1(\alpha)=0\, .\tag{19} \end{equation} La matrice \([Q+\alpha D-\lambda_1(\alpha) I]\) a un noyau de dimension 1, dirigé par \(w_1(\alpha)\). Toujours avec les notations de la section 2.2, la matrice transposée \(\,[Q^\mathsf{T}+\alpha D-\lambda_1(\alpha) I]\) a un noyau de dimension 1, dirigé par \(v_1(\alpha)\). On prend le produit scalaire de (19) avec \(\,v_1(\alpha)\) \[\langle v_1(\alpha),Dw_1(\alpha)\rangle = 0.\] D'après (12), ceci équivaut à \(\lambda_1'(\alpha)=0\). Avec \(\,m > 0\) et \(\lambda_1'(1) > 0\,\), on a \(\alpha=\alpha^*\). On a donc \(\,\omega=\Lambda\).
Étudions maintenant le comportement pour n grand d'un vecteur propre \(\,(\pi_{n,i})\) associé à la valeur propre \(\omega_1\). Essayons directement une solution de (4) avec \[ \pi_{n,i}= \Pi^n \left (\frac{k_i}{n^{\beta}}+\frac{h_i}{n^{\beta+1}}+\cdots \right ), \quad n\to +\infty. \] Pour n grand, on a \[(n+1)^{-\delta}=n^{-\delta} (1+1/n)^{-\delta} \simeq n^{-\delta} (1-\delta/n) \simeq n^{-\delta} - \delta\, n^{-\delta-1}\] et \[(n-1)^{-\delta}\simeq n^{-\delta}+\delta\, n^{-\delta-1}.\] On a donc \begin{align*} n\, \pi_{n,i} &\simeq \Pi^n \left (\frac{k_i}{n^{\beta-1}}+\frac{h_i}{n^{\beta}}+\cdots \right ),\\ (n\pm 1)\pi_{n\pm 1,i} &\simeq \Pi^{n\pm 1} \left (\frac{k_i}{n^{\beta-1}}\pm \frac{(1-\beta)k_i}{n^{\beta}}+\frac{h_i}{n^{\beta}}+\cdots \right ), \end{align*} pour n grand. On voit que les expressions en \(\ \Pi^n/n^{\beta-1}\) dans (4) donnent \[0 = -(a_i+b_i)k_i + b_i \, k_i\, \Pi + a_i\, k_i / \Pi\, .\] On a ainsi \[(\Pi-1)(b_i-a_i/\Pi)k_i=0,\quad \forall i.\] Avec \(\,a_1/b_1=\max_i a_i/b_i\,\), on prend \(\Pi=a_1/b_1\), \(k_1\neq 0\) et \(k_i=0\) si \(i\neq 1\). Avec \(\,q_i=-Q_{i,i}\,\), les expressions en \(\,\Pi^n/n^\beta\) dans (4) sont \begin{equation} \omega_1\, k_i = (b_i \Pi + a_i/\Pi -a_i -b_i) h_i + (a_i/\Pi - b_i \Pi)(\beta-1) k_i + \sum_j Q_{i,j} k_j\, . \tag{20} \end{equation} On a ainsi \[\omega_1\, k_1=(b_1-a_1)(\beta-1)k_1-q_1\, k_1\] et \[0 = (a_1-b_1)(b_i/b_1-a_i/a_1)h_i + Q_{i,1} k_1,\quad \forall i\neq 1.\] On en déduit \begin{align} \beta&=1+\frac{\omega_1+q_1}{b_1-a_1}\, ,\quad h_i = \frac{Q_{i,1}}{(b_1-a_1)(b_i/b_1-a_i/a_1)}\, k_1\quad \forall i\neq 1.\tag{21} \end{align}
Alternativement, on étudie le système (5) au voisinage de \(x=b_1/a_1\). On a \[G_1(x) \sim ( x-b_1/a_1)^{(\omega_1+q_1)/(b_1-a_1)}.\] Pour la valeur propre \(\omega_1\,\), on peut choisir le vecteur propre associé de sorte que \(\pi_{n,i} > 0\) pour \(n\geq 1\). Pour la série entière \(\,G_i(x)\,\), considérons le point singulier le plus proche de 0 dans le plan complexe. Ce point se trouve sur l'axe x > 0, d'après un théorème de A. Pringsheim (Queffélec et Zuily, 2013, p. 54). D'après (Flajolet et Sedgewick, 2009), on a alors \[\pi_{n,1}\sim (a_1/b_1)^n / n^{1+(\omega_1+q_1)/(b_1-a_1)},\quad n\to +\infty,\] à une constante multiplicative près. C'est bien ce que l'on a trouvé.
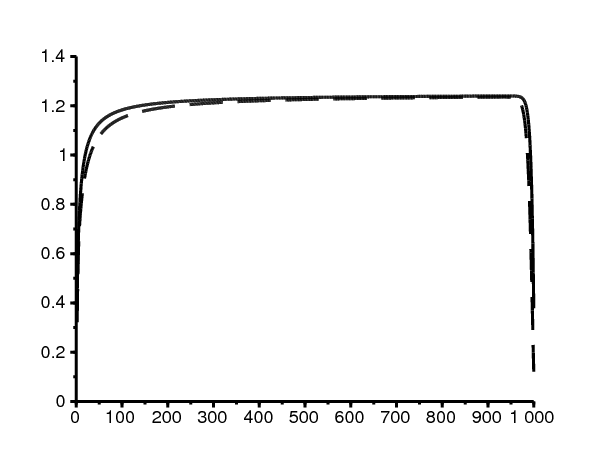
Exemple numérique. Reprenons notre exemple numérique (15), avec \(\,a_1= \mbox{2,5}\). La figure 2 montre le comportement asymptotique du vecteur propre associé à la valeur propre \(\,\mu_N\), pour \(N=1000\). Ici on a \(\,\Lambda=-1\). On a donc \(\,\beta=1\) et \(k_1/h_2= \mbox{0,3}\). La figure semble bien confirmer les résultats asymptotiques obtenus, vu qu'il ne faut pas tenir compte de l'effet de bord près de n=N.
On soupçonne \(\pi_{n,i}\simeq k_i/n^\beta\) ou \(\pi_{n,i}\simeq k_i (\log n)/n^\beta\). Dans les deux cas, les expressions dominantes dans (4) donnent \begin{equation} \omega\, k_i = (\beta-1)(a_i-b_i) k_i + \sum_j Q_{i,j} k_j\, .\tag{22} \end{equation} Autrement dit, \(\omega\) est une valeur propre de la matrice \(Q+(\beta-1)D\). En effet, dans le cas où l'on cherche une solution de la forme \(\,\pi_{n,i}\simeq k_i/n^\beta\,\), on est comme dans (20) avec \(\Pi=1\). Quant au cas où \[\pi_{n,i}\simeq (\log n) \left [\frac{k_i}{n^\beta}+\frac{h_i}{n^{\beta+1}}+\cdots\right ],\] on a \begin{align*} (n\pm 1) \pi_{n\pm 1,i} &\simeq \left (\log n \pm \frac{1}{n} \right ) \left [\frac{k_i}{(n\pm 1)^{\beta-1}} + \frac{h_i}{(n\pm 1)^\beta} \right ] +\cdots\\ &\simeq (\log n) \left [\frac{k_i}{n^{\beta-1}} + \frac{h_i \pm (1-\beta)k_i}{n^\beta}\right ] +\cdots\, , \end{align*} ce qui conduit à nouveau à l'équation (22). Ceci suggère que \(\,\beta=1+\alpha^*\) si \(\lambda_1'(1) > 1\) et \(\beta=2\) si \(\lambda_1'(1)\leq 0\). Dans les deux cas, le rayon de convergence des \(\ G_i(x)\) serait égal à 1.
On peut considérer l'équation différentielle d'ordre 2 satisfaite par \(G_1(x)\) plutôt que le système différentiel d'ordre 1 pour \(G_1(x)\) et \(G_2(x)\). On obtient \begin{align*} &(1-x)^2 (a_1 x-b_1)(a_2 x-b_2) \frac{d^2G_1}{dx^2}\\ &+ (1-x)\Bigl \{\bigl [\omega+q_1+a_1(1-2x)+b_1\bigr ](a_2x-b_2)+(\omega+q_2)(a_1x-b_1)\Bigr \}\frac{dG_1}{dx}\\ &+\Bigl [(\omega+q_1)(\omega+q_2)-q_1 q_2\Bigr ] G_1=0\, . \end{align*} En divisant par \((1-x)^2 (a_1 x-b_1)(a_2 x-b_2)\) et en décomposant en éléments simples la fraction rationnelle, on obtient \begin{align*} 0=&\frac{d^2G_1}{dx^2}+ \left [ \frac{1-\frac{\omega+q_1}{a_1-b_1}-\frac{\omega+q_2}{a_2-b_2}}{x-1}+ \frac{1+\frac{\omega+q_1}{a_1-b_1}}{x-\frac{b_1}{a_1}} + \frac{\frac{\omega+q_2}{a_2-b_2}}{x-\frac{b_2}{a_2}} \right ] \frac{dG_1}{dx}\\ & + \left [\frac{(\omega+q_1)(\omega+q_2)-q_1 q_2}{(a_1-b_1)(a_2-b_2)}\, \frac{(1-\frac{b_1}{a_1})(1-\frac{b_2}{a_2})}{x-1}\right ] \frac{G_1}{(x-1) (x-\frac{b_1}{a_1})(x-\frac{b_2}{a_2}) }\, . \end{align*} Supposons que les nombres \(b_1/a_1\), \(b_2/a_2\,\) et 1 soient tous distincts. On reconnaît une équation différentielle de la forme \begin{align*} \frac{d^2G_1}{dx^2}&+ \left [ \frac{1-k_0-k_0'}{x-x_0} + \frac{1-k_1-k_1'}{x-x_1} + \frac{1-k_2-k_2'}{x-x_2} \right ] \frac{dG_1}{dx}\\ & + \Biggl [ \frac{k_0 k'_0 (x_0-x_1)(x_0-x_2)}{x-x_0}+\frac{k_1 k'_1 (x_1-x_2)(x_1-x_0)}{x-x_1}\\ &\quad \quad + \frac{k_2 k'_2 (x_2-x_1)(x_2-x_0)}{x-x_2} \Biggr ] \frac{G_1}{(x-x_0)(x-x_1)(x-x_2)} = 0, \end{align*} c'est-à-dire une équation différentielle de Riemann (Roseau, 1997, p. 229) avec trois points singuliers \(x_0=1\), \(x_1=b_1/a_1\) et \(x_2=b_2/a_2\). Les exposants caractéristiques de cette équation sont respectivement \[(k_0,k'_0)=(\alpha_+,\alpha_-),\quad (k_1,k'_1)=\left (0,-\frac{\omega+q_1}{d_1}\right ), \quad (k_2,k'_2)=\left (0,1-\frac{\omega+q_2}{d_2}\right ), \] avec \(\alpha_+\) et \(\alpha_-\,\) solutions de (13). L'ensemble des solutions peut donc s'écrire avec la notation de Riemann \[G_1(x)=P \left \{ \begin{array}{ccccccc} 1&\quad & \frac{b_1}{a_1} &\quad & \frac{b_2}{a_2} &\quad & \\ \alpha_+ && 0 && 0 && x \\ \alpha_- && -\frac{\omega+q_1}{d_1} && 1-\frac{\omega+q_2}{d_2} && \end{array} \right \}.\] D'après (Roseau, 1997, p. 229), on peut écrire \[G_1(x)=\left (\frac{x-1}{x-\frac{b_1}{a_1}}\right )^{\alpha_+}\! P \left \{ \begin{array}{ccccccc} 1&\quad& \frac{b_1}{a_1} &\quad& \frac{b_2}{a_2} &\quad& \\ 0 && \alpha_+ && 0 && x \\ \alpha_- - \alpha_+ && \alpha_+-\frac{\omega+q_1}{d_1} && 1-\frac{\omega+q_2}{d_2} && \end{array} \right \}.\] On définit \[\mathcal{A}=\alpha_+,\quad \mathcal{B}=\alpha_+-\frac{\omega+q_1}{d_1},\quad \mathcal{C}=1+\alpha_+-\alpha_-.\] On se ramène au cas de l'équation différentielle hypergéométrique \[y=\frac{x-1}{x-\frac{b_1}{a_1}}\ \frac{\frac{b_2}{a_2}-\frac{b_1}{a_1}}{\frac{b_2}{a_2}-1}\, ,\] ce qui traduit l'égalité \((y,0;\infty,1)=(x,1;b_1/a_1,b_2/a_2)\,\) entre quotients anharmoniques. On a ainsi \[G_1(x)=\left (\frac{x-1}{x-\frac{b_1}{a_1}}\right )^{\alpha_+}\! P \left \{ \begin{array}{ccccccc} 0&\quad& \infty &\quad & 1 &\quad& \\ 0 && \mathcal{A} && 0 & & y \\ 1-\mathcal{C} && \mathcal{B} && \mathcal{C}-\mathcal{A}-\mathcal{B} && \end{array} \right \}.\] La fonction hypergéométrique est \[F(\alpha,\beta;\gamma;z)=\sum_{n\geq 0} \frac{(\alpha)_n (\beta)_n}{(\gamma)_n}\, \frac{z^n}{n!}, \quad |z| < 1\] avec la notation \((\alpha)_n=\alpha (\alpha+1)\ldots (\alpha+n-1)\). Si x est au voisinage de 1, la variable y est au voisinage de 0. D'après la théorie de l'équation différentielle hypergéométrique, il existe des constantes \(\,\kappa_1\) et \(\kappa_2\) avec \begin{align*} G_1(x)=\left (\frac{x-1}{x-\frac{b_1}{a_1}}\right )^{\alpha_+} \Bigl [&\kappa_1 F\left (\mathcal{A}, \mathcal{B} ; \mathcal{C}; y\right )\\ &+\kappa_2\, y^{1-\mathcal{C}}\, F(\mathcal{A}-\mathcal{C}+1,\mathcal{B}-\mathcal{C}+1;2-\mathcal{C};y) \Bigr ], \end{align*} pourvu que \(\mathcal{C}\neq 1\,\), c'est-à-dire \(\alpha_-\neq \alpha_+\). Les solutions avec un exposant fuchsien \(\,\alpha_+\,\) en x=1 correspondent à \(\kappa_2=0\) \begin{equation} G_1(x)=\kappa_1 \left (\frac{x-1}{x-\frac{b_1}{a_1}}\right )^{\alpha_+} F\left (\mathcal{A}, \mathcal{B} ; \mathcal{C}; y\right ).\tag{23} \end{equation}
On suppose par exemple \(\,a_2/b_2 < a_1/b_1 < 1\,\). On prend \(\,\alpha_+=1\) pour la fonction propre associée à \(\omega_1=s(Q+D)\). On choisit \(\kappa_1\) pour que \(G_1(0)=1\). On a alors \[\alpha_-=\frac{\omega_1+q_1}{d_1}+\frac{\omega_1+q_2}{d_2}-1\] d'après (13). On définit \[\xi= \frac{\frac{b_2}{a_2}-2\frac{b_1}{a_1}+\frac{b_1 b_2}{a_1 a_2}}{2\frac{b_2}{a_2}-\frac{b_1}{a_1}-1}\, .\] C'est la valeur de x pour laquelle \(\ y=-1\). On a \(\,1 < \xi < b_1/a_1\). La variable y décroît si 0 < x < ξ avec des valeurs \[\frac{\frac{a_1}{b_1}\, \frac{b_2}{a_2} - 1}{\frac{b_2}{a_2}-1}\in ]0,1[ \quad \searrow \quad -1.\] Dans le cas \(\,\xi < x < b_1/a_1\), l'expression (23) doit être remplacée \begin{align} G_1(x)&=\kappa_1 \left (\frac{x-1}{x-\frac{b_1}{a_1}}\right )^{\alpha_+} (1-y)^{-\mathcal{A}}\, F\left (\mathcal{A}, \mathcal{C}-\mathcal{B} ; \mathcal{C}; \frac{y}{y-1}\right )\nonumber \\ &=\kappa_1 \left (\frac{x-1}{x-\frac{b_2}{a_2}}\ \frac{\frac{b_2}{a_2}-1}{\frac{b_1}{a_1}-1}\right )^{\alpha_+} F\left (\mathcal{A}, \mathcal{C}-\mathcal{B} ; \mathcal{C}; \frac{y}{y-1}\right ),\tag{24} \end{align} qui est l'expression (18) du §182 de (C. Jordan, 1896), dans laquelle l'argument \(\frac{y}{y-1}\) croît de 1/2 jusqu'à 1.
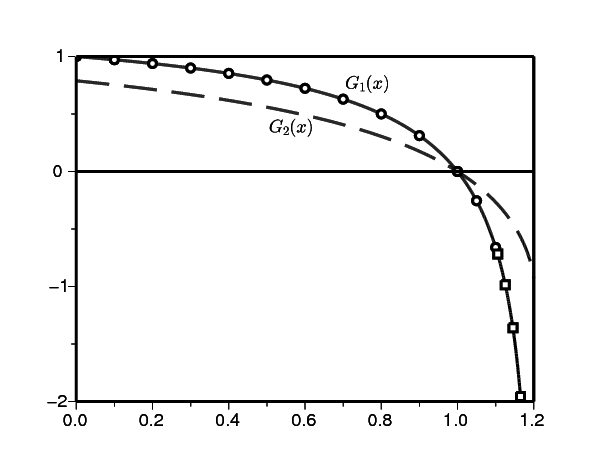
Reprenons notre exemple numérique (15), avec \(a_1=\mbox{2,5}\). La figure 3 montre les fonctions génératrices \(\,G_1(x)\) et \(G_2(x)\) construites avec le vecteur propre associé à \(\mu_N\). Ici \(N=4000\,\) avec la normalisation \(G_1(0)=1\). On utilise la méthode de Horner pour évaluer les séries génératrices. On les compare avec les formules (23) et (24). Ici on a \(\,\xi\simeq \mbox{1,105}\). Le facteur multiplicatif de normalisation a été choisi de sorte que les fonctions obtenues par les deux méthodes soient superposables.
On suppose par exemple \(\,a_1/b_1 > 1 > a_2/b_2\). On a maintenant \[\,0 < b_1/a_1 < \xi < 1.\] L'expression (23) ne convient plus car la variable \(y\) diverge en \(x=b_1/a_1 < 1\). Avec \(\,0 < x < \xi\,\), \(y^{-1}\) est une fonction décroissante qui varie d'un nombre compris entre 0 et 1 jusqu'à −1. On prend sur cet intervalle l'expression (32) de (C. Jordan, 1896, §182), \begin{align} G_1(x) &= \kappa_1 \left (\frac{x-1}{x-\frac{b_1}{a_1}}\right )^{\alpha_+} y^{-\mathcal{A}}\, F\left (\mathcal{A},\mathcal{A}+1-\mathcal{C}; \mathcal{A}+1-\mathcal{B} ; y^{-1}\right )\nonumber\\ &=\kappa_1 \left (\frac{\frac{b_2}{a_2}-1}{\frac{b_2}{a_2}-\frac{b_1}{a_1}}\right )^{\alpha_+} F\left (\mathcal{A},\mathcal{A}+1-\mathcal{C}; \mathcal{A}+1-\mathcal{B} ; y^{-1}\right ),\tag{25} \end{align} avec \(\alpha_+=1\), \(\omega_1=s(Q+D)\) et \(\kappa_1\) de sorte que \(G_1(0)=1\). En revanche, sur l'intervalle \(\,\xi < x < 1\,\), on prend l'expression (34) de (C. Jordan, 1896, §182), dans laquelle l'argument \((1-y)^{-1}\) croît de 1/2 à 1: \begin{align} G_1(x) &= \kappa_1 \left (\frac{x-1}{x-\frac{b_1}{a_1}}\right )^{\alpha_+} y^{-\mathcal{A}} (1-1/y)^{-\mathcal{A}}\, F\left (\mathcal{A},\mathcal{C}-\mathcal{B}; \mathcal{A}+1-\mathcal{B} ; (1-y)^{-1}\right )\nonumber\\ &=\kappa_1 \left ( \frac{x-1}{x-\frac{b_2}{a_2}} \ \frac{\frac{b_2}{a_2}-1}{1-\frac{b_1}{a_1}} \right )^{\alpha_+} F\left (\mathcal{A},\mathcal{C}-\mathcal{B}; \mathcal{A}+1-\mathcal{B} ; (1-y)^{-1}\right ) . \tag{26} \end{align}
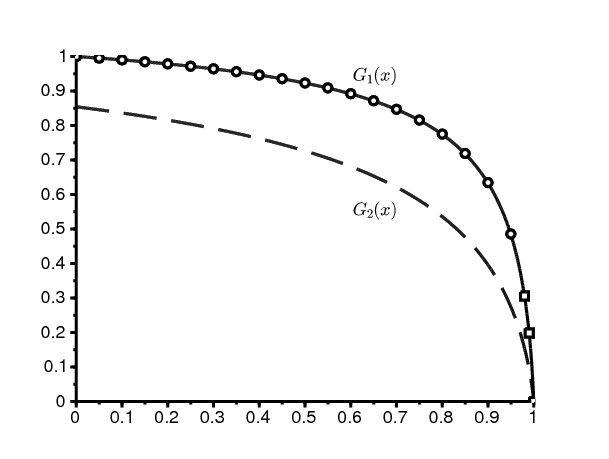
Reprenons notre exemple numérique (15), avec \(a_1=\mbox{3,2}\). La figure 4 montre les formules (25) et (26). Elles coïncident bien avec la fonction génératrice construite avec le vecteur propre. Ici on a \(\xi\simeq \mbox{0,97}\).
Les expressions (25) et (26) ne sont probablement plus valables, même si \(\alpha_+=\alpha_-=\alpha^*\). Elles doivent être remplacées par des expressions contenant un terme logarithmique. Avec \(\,a_1=\mbox{3,5}\,\), on a \(\Lambda=-\mbox{0,2}\) et \(\alpha^*=\mbox{0,6}\,\) d'après les formules (14). On n'est pas parvenu à obtenir un graphique suggestif dans ce cas.
Pour un processus de branchement sous-critique dans un environnement aléatoire avec des environnements indépendants identiquement distribués, \((Z_n)_{n=0,1,\ldots}\), on a \begin{equation} \lim_{n\to \infty} \left [\mathbb{P}(Z_n > 0) \right ]^{1/n} = \min_{0\leq \alpha \leq 1} \mathbb{E} ( f'(1)^\alpha)\, . \tag{27} \end{equation} \(f(x)\,\) désigne la fonction génératrice (Dekking, 1988 ; Geiger et coll., 2003). Soit μ le minimum dans le côté droit de (27). Dans le cas « faiblement sous-critique» où \[\mathbb{E} (f'(1) \log f'(1)) > 0,\] on a \[\mathbb{P}(Z_n > 0)\sim c\, n^{-3/2} \mu^n,\quad n\to \infty\] pour une constante \(c > 0\). Dans le cas « fortement sous-critique» où \[\mathbb{E} (f'(1) \log f'(1)) < 0,\] on a \(\mu=\mathbb{E} (f'(1))\) et \[\mathbb{P}(Z_n > 0)\sim c\, \mu^n,\quad n\to \infty\] pour une constante \(c > 0\). Le processus est sous-critique si \(\,\mathbb{E}(\log f'(1)) < 0\).
Retournons à notre processus de naissance et de mort. Limitons nous au cas particulier de deux environnements: \(\,K=2\). On définit \[\phi_{i,t}(x)=\frac{b_i(1-x)e^{(a_i-b_i)t}+a_ix-b_i}{a_i(1-x)e^{(a_i-b_i)t}+a_ix-b_i}\, .\] Avec \(\,a_i\neq b_i\,\), c'est la fonction génératrice du nombre d'individus au bout d'un temps \(t\) partant d'un individu au temps 0 dans l'environnement \(i\,\) (Hillion, 1986). Dans tous les cas, \[\phi_{i,t}'(1)=e^{(a_i-b_i)t}=e^{d_i\, t}.\] Au bout d'un temps \(t_1\,\), l'environnement bascule de l'état 1 vers l'état 2. Au bout d'un temps \(t_2\,\), l'environnement bascule de nouveau vers l'état 1. Les densités de probabilités associées sont \(\,q_1 e^{-q_1 t_1}\) et \(q_2 e^{-q_2 t_2}\). Considérons alors la chaîne de Markov incluse ne regardant que le changement entre le temps 0 et le temps \(t_1+t_2\), \((Z_n)_{n=0,1,\ldots}\). Appelons cela une génération. La fonction génératrice est \[f(x)=\phi_{2,t_2}(\phi_{1,t_1}(x)).\] En particulier, \(f'(1)=e^{d_1 t_1+d_2 t_2}\). Ce processus de branchement est sous-critique. En effet, on a \begin{align*} \mathbb{E}(\log f'(1))&=\int_0^\infty \!\!\!\int_0^\infty \!\!\!q_1 e^{-q_1t_1} q_2 e^{-q_2 t_2} [d_1 t_1+d_2 t_2] dt_1\, dt_2 =\frac{d_1}{q_1}+\frac{d_2}{q_2} < 0\, \end{align*} parce que \(R_0 < 1\). Le processus est fortement sous-critique lorsque \begin{align} \mathbb{E}(f'(1)\log f'(1)) &=\int_0^\infty \!\!\!\int_0^\infty \!\!\! q_1 e^{-q_1t_1} q_2 e^{-q_2 t_2} e^{d_1 t_1} e^{d_2 t_2} [d_1 t_1+d_2 t_2] dt_1\, dt_2\nonumber\\ &=\frac{q_1 q_2}{(q_1-d_1)(q_2-d_2)} \left [ \frac{d_1}{q_1-d_1}+\frac{d_2}{q_2-d_2}\right ] < 0\, .\tag{28} \end{align} Dans ce cas, on a \begin{align*} \mu=\mathbb{E}(f'(1))&=\int_0^\infty \!\!\!\int_0^\infty \!\!\! q_1 e^{-q_1t_1} q_2 e^{-q_2 t_2} e^{d_1 t_1} e^{d_2 t_2} dt_1\, dt_2=\frac{q_1 q_2}{(q_1-d_1)(q_2-d_2)}\, . \end{align*} Noter que si \(d_1 < 0\) et \(d_2 < 0\,\), alors le processus est fortement sous-critique. Dans le cas faiblement sous-critique, on a \begin{align*} \mathbb{E} (f'(1)^\alpha)&= \frac{q_1 q_2}{[q_1-\alpha d_1][q_2-\alpha d_2]}\, \end{align*} et un petit calcul montre \[\mu=-4\, \frac{\frac{q_1}{d_1}\, \frac{q_2}{d_2}}{\left (\frac{q_1}{d_1} -\frac{q_2}{d_2}\right )^2}\, . \] Noter que ce nombre est \( < 1\) si et seulement si \(R_0 < 1\).
Pour notre exemple numérique, la formule (28) montre que la chaîne de Markov incluse est fortement sous-critique lorsque \(a_1 < \mbox{3,4}\). Curieusement, ce seuil diffère de celui séparant les cas \(\,\Lambda=s(Q+D)\) et \(\Lambda=s(Q+\alpha^* D)\) avec \(0 < \alpha^* < 1\,\) pour le processus linéaire de naissance et de mort. Ce dernier seuil était \(\,\simeq \mbox{3,2829}\) d'après la section 3. Cependant le taux auquel la chaîne de Markov incluse converge vers l'extinction n'a pas grand-chose à voir avec le taux auquel le processus en temps continu en fait de même.
De nombreux points restent à éclaircir concernant le comportement des valeurs propres et vecteurs propres. Parmi les généralisations possibles, on peut penser que si les coefficients \(\,a_i\), \(b_i\) et \(Q_{i,j}\,\) sont des fonctions périodiques du temps t, alors \(\,\omega_1\) sera égal à \(\min \{f(Q(\cdot)+\alpha D(\cdot));\ 0\leq \alpha \leq 1\}\). \(\,f(\cdot)\,\) désigne l'exposant de Floquet dominant et remplace la borne spectrale.
On remercie Vincent Bansaye, Anne Duval et Bruno Sericola pour leurs remarques et suggestions.