N. Bacaër: La taille finale des épidémies dans un environnement périodique. C. R. Biol. 342 (2019) p. 119-123.
doi : 10.1016/j.crvi.2019.07.001
Nicolas Bacaër
Institut de recherche pour le développement
Les Cordeliers, Paris, France
nicolas.bacaer@ird.fr
Il est difficile de prédire la taille finale d'une épidémie comme celle de dengue qui sévit actuellement à La Réunion, d'autant qu'il faut tenir compte de la saisonnalité. Dans cet article, on se propose d'étudier d'un point de vue théorique comment, dans le cadre d'un modèle très simple de type S-I-R pour une maladie à transmission directe, un environnement saisonnier périodique modifie la taille finale d'une épidémie. On obtient des résultats analytiques en supposant que l'amplitude de la saisonnalité est faible.
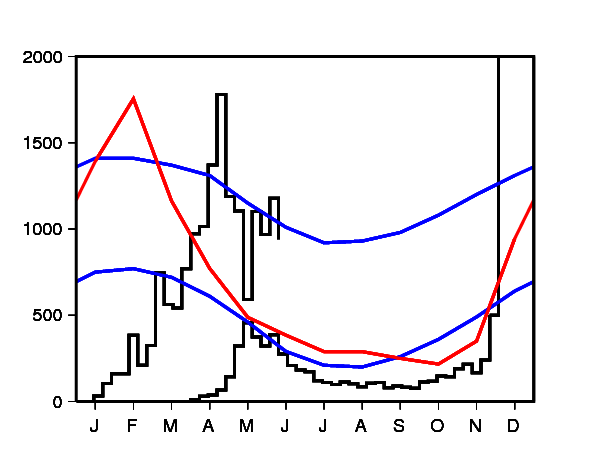
Une épidémie de dengue sévit actuellement sur l'île de La Réunion, dans l'océan Indien. Plus de 5000 cas ont été confirmés biologiquement entre janvier et juin 2018, et plus de 16000 cas évocateurs de la dengue ont été signalés (figure 1). Fin juin, du fait de l'arrivée de l'hiver austral mais aussi de la lutte antivectorielle, l'épidémie recule. Cependant il est difficile de prévoir si le nombre d'infections diminuera suffisamment pour empêcher une seconde vague épidémique à la fin 2018, lorsque les conditions climatiques seront plus favorables aux moustiques vecteurs de la maladie. C'est cette deuxième vague qui en 2006 avait infecté presque un tiers de la population avec le chikungunya.

Il serait tentant de modéliser mathématiquement la propagation de la dengue de manière réaliste tout en limitant la complexité du modèle pour n'avoir que quelques paramètres inconnus, comme on a essayé de le faire pour le chikungunya dans (Bacaër, 2007). Mais les incertitudes qui pèsent sur ces paramètres et sur leur dépendance par rapport aux variables climatiques sont si grandes que les résultats numériques risquent fort d'être assez douteux (Raoult, 2016). On se contentera ci-dessous d'un modèle épidémique extrêmement simplifié à transmission directe et non vectorielle, qui ne prétend donc pas pouvoir être appliqué au cas de la dengue à La Réunion. Cela n'aurait pas vraiment de sens de vouloir ajuster ses paramètres aux données épidémiques. L'objectif est plutôt d'attirer l'attention sur la question de la taille finale d'une épidémie dans un environnement saisonnier périodique. Cette question qui a été peu étudiée d'un point de vue théorique.
Même les modèles mathématiques les plus simples qui tiennent compte de la saisonnalité présentent de nombreuses difficultés. On sait depuis longtemps que pour les modèles de maladies endémiques, un coefficient périodique peut engendrer des oscillations avec une période différente, voire des oscillations chaotiques (Choisy et Cazelles, 2009). Dans (Bacaër, 2007) inspirée de l'épidémie de chikungunya à La Réunion, on a vu par ailleurs que même la notion classique de reproductivité, introduite par Lotka (1939), devait être définie avec quelques précautions dans les modèles périodiques. En effet, l'inégalité \[\mathbf{R_0} > 1\] doit traduire l'instabilité de la situation sans épidémie. La difficulté apparaît notamment pour les modèles avec au moins deux compartiments d'infectés.
Dans (Bacaër et Gomes, 2009), on a abordé le modèle S-I-R périodique, simple généralisation du modèle classique de Kermack et McKendrick (Hillion, 1986, p. 75) : \begin{equation} \frac{dS}{dt} = -a(t) \frac{S I}{N},\quad \frac{dI}{dt} = a(t) \frac{S I}{N} - b\, I,\quad \frac{dR}{dt}=b\, I. \tag{1} \end{equation}
En combinant méthodes numériques et méthodes analytiques, on étudie ici plus attentivement la taille finale de l'épidémie dans le cas particulier où \[a(t)=a_0(1+\varepsilon \, \phi(t))\] avec
Dans le cas \(\phi(t)=\cos(\omega t)\), si le nombre de personnes infectées au départ est petit devant la taille de la population (\(i\ll N\)), si \(\mathbf{R_0}=a_0/b > 1\) avec \(\mathbf{R_0}\) proche de 1, et si \(i/N \ll (\mathbf{R_0}-1)^2\,\), alors on détermine analytiquement le coefficient correcteur c en fonction des paramètres \(N\), \(i\), \(a_0\), \(b\), \(t_0\) et ω du modèle. On trouve que l'environnement périodique augmente la taille finale de l'épidémie (c>0) si \[a(t_0+\tau) > a_0.\] \(t_0+\tau\) est le moment où l'épidémie atteindrait son pic dans un environnement constant.
(Bacaër et Gomes, 2009) montre, à partir du système différentiel (1), que :
On peut évaluer numériquement cette intégrale. On utilise d'abord le logiciel de calcul numérique Scilab et sa fonction ode, voir http://www.scilab.org/fr, pour résoudre le système différentiel (1) avec ε=0. On obtient ainsi \((S_0(t),I_0(t),R_0(t))\) pour un ensemble discret de valeurs de t, avec un petit pas de temps. On en déduit en particulier la valeur \(R_0(\infty)\). Puis on calcule l'intégrale avec cette même discrétisation du temps. On en déduit la valeur du coefficient c.
Prenons un exemple :
\[\phi(t)=\cos (\omega t),\quad \omega=2\pi/T, \quad N=10\, 000, \quad i=1,\]
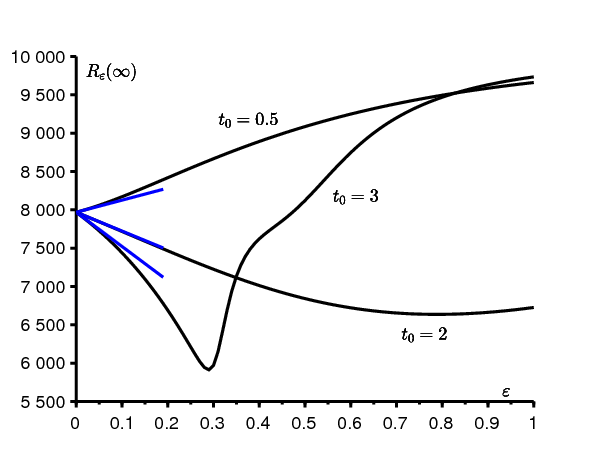
\(T=12\) mois, \(a_0=10\)/mois et \(b=5\)/mois. Alors la reproductivité est \(\mathbf{R_0}=2\). La taille finale de l'épidémie dans un environnement constant est \(R_0(\infty)\simeq 7\, 968\). La figure 2 montre la fonction \(\varepsilon \mapsto R_\varepsilon(\infty)\), \(0\leq \varepsilon \leq 1\). \(t_0\) prend trois valeurs différentes, qui correspondent à trois moments différents d'introduction du premier cas infecté dans la population : 0,5 mois, 2 mois ou 3 mois. La figure montre aussi l'approximation \(R_0(\infty)+N c\, \varepsilon\) pour ε petit. Le coefficient correcteur c est calculé selon la formule (3). On observe que le coefficient c peut être positif ou négatif, de sorte que la taille finale de l'épidémie peut être plus grande ou plus petite que dans un environnement constant. On observe aussi que pour \(t_0=3\) mois, la fonction \(R_\varepsilon(\infty)\) varie en fonction de ε de manière plus compliquée que pour les deux autres valeurs de \(t_0\). En particulier, cette fonction n'est décroissante que tant que ε<0,3 .
Kermack et McKendrick ont trouvé une approximation pour la courbe épidémique à partir de l'équation exacte suivante \[\frac{dR_0}{dt} = b(N-s \, e^{-a_0R_0/(Nb)}-R_0).\] Voir par exemple (Bacaër, 2012, §2) ou (Gani, 1975, p. 235). L'approximation \(e^{-x}= 1-x+x^2/2+o(x^2)\) conduit à une équation de Ricatti résoluble et à une courbe en cloche symétrique pour \(I_0(t)\), \[I_0(t) \simeq \frac{N\, X}{\mathrm{ch}^2(Y (t-t_0)-Z)},\quad \forall t > t_0,\] avec \[ X=\frac{b^2 N\, W^2}{2\, a_0^2\, s},\quad Y=\frac{b\, W}{2}, \quad \mathrm{th}(Z) = \frac{\frac{a_0\, s}{b\, N}-1}{W},\] et \[W=\sqrt{\left (\frac{a_0\, s}{b\, N}-1\right )^2+2\, \frac{s\, i}{N^2} \, \frac{a_0^2}{b^2}} \, .\] Ici, \(\mathrm{ch}(\cdot)\) et \(\mathrm{th}(\cdot)\) désignent le cosinus hyperbolique et la tangente hyperbolique et \(s=N-i\). L'approximation pour \(I_0(t)\) est d'autant meilleure que \(a_0R_0(\infty)/(Nb)\), la valeur maximale du terme dans l'exponentielle, est petit par rapport à 1. On a alors \begin{equation} c\simeq \frac{a_0 X }{\frac{N}{N-R_0(\infty)}-\frac{a_0}{b}} \, \int_{t_0}^\infty \frac{\phi(t)}{\mathrm{ch}^2(Y (t-t_0)-Z)}\, dt\, . \tag{4} \end{equation}
Supposons plus précisément que \[\mathbf{R_0}=a_0/b\to 1,\quad \mathbf{R_0} > 1,\quad (i/N)/(\mathbf{R_0}-1)^2\to 0.\] Autrement dit, \(\mathbf{R_0}\) est proche de 1 et \(i/N \ll (\mathbf{R_0}-1)^2\). On a alors \(i\to 0\) et \(R_0(\infty)\to 0\) d'après l'équation (2) avec \(\varepsilon=0\). On a aussi \(i/N \ll (\mathbf{R_0}-1)\,\), \[W\sim \frac{a_0}{b}-1,\quad X\sim \frac{(1-b/a_0)^2}{2},\quad Y\sim \frac{a_0-b}{2}\] et \(1-\mathrm{th}(Z)\sim\frac{i/N}{(b/a_0-1)^2}\). On a donc \(Z\to +\infty\), \(1-\mathrm{th}(Z)\sim 2\, e^{-2Z}\) et \[Z\sim \frac{1}{2} \log \frac{2(b/a_0-1)^2}{i/N}\, .\] Avec \(\tau=Z/Y\), c'est en \(t=t_0+\tau\) que l'approximation de \(I_0(t)\) atteint son pic. On a \(Y\to 0\) et \(\tau\to +\infty\). Après le changement de variable \(t=t_0+\tau+u\,\), on remarque que la fonction \(1/\mathrm{ch}^2(Yu)\) est presque nulle en dehors du voisinage de \(u=0\). Par conséquent, \[ \int_{-\tau}^\infty \frac{\phi(t_0+\tau+u)}{\mathrm{ch}^2(Y u)}\, du \simeq \int_{-\infty}^\infty \frac{\phi(t_0+\tau+u)}{\mathrm{ch}^2(Y u)}\, du \, . \]
Cette dernière intégrale se calcule explicitement lorsque \(\phi(t)=\cos(\omega t)\). En effet, \[\int_{-\infty}^\infty \frac{\cos(\omega (t_0+\tau+u))}{\mathrm{ch}^2(Y u)}\, du = \cos(\omega (t_0+\tau)) \int_{-\infty}^\infty \frac{\cos(\omega u)}{\mathrm{ch}^2(Y u)}\, du\] puisque l'intégrale avec la fonction impaire \(\sin(\omega u)\) est nulle. D'après la formule dans l'appendice de (Bacaër, 2015), on a \[\int_{-\infty}^{\infty} \frac{\cos(\omega u)}{\mathrm{ch}^2(Y u)}\, du = \frac{\frac{\pi \omega}{Y^2}}{\mathrm{sh}(\frac{\pi \omega}{2Y})}\, .\] \(\mathrm{sh}(\cdot)\) désigne le sinus hyperbolique. Avec les équivalents de X et Y déjà obtenus, on arrive finalement à \begin{equation} c \simeq \frac{\cos(\omega (t_0+\tau))}{\frac{N}{N-R_0(\infty)}-\frac{a_0}{b}} \, \frac{\frac{2\pi \omega}{a_0}}{\mathrm{sh}(\frac{\pi \omega}{a_0-b})}\, . \tag{5} \end{equation} On voit que le signe de \(c\) est le même que celui de \(\cos(\omega (t_0+\tau))\). Donc l'environnement périodique augmente la taille finale de l'épidémie si \(a(t_0+\tau) > a_0\). \(t_0+\tau\) est le moment où l'épidémie atteindrait son pic dans un environnement constant.
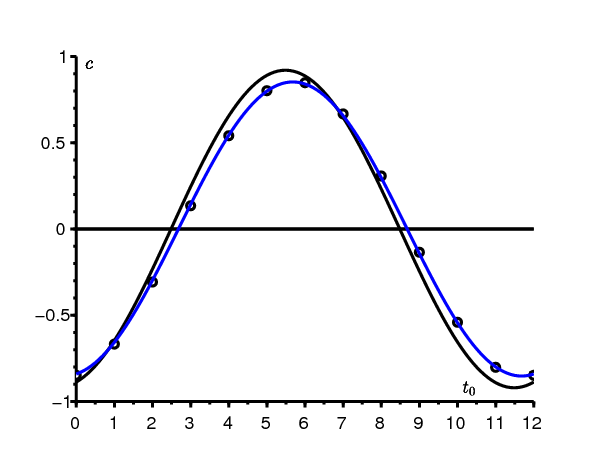
Comme exemple, prenons les mêmes valeurs des paramètres que dans la figure 2 sauf que \(a_0=6\)/mois pour avoir une reproductivité plus proche de 1 : \(\mathbf{R_0}=\mbox{1,2}\,\). (Gani, 1975, p. 240) indique d'ailleurs que l'approximation en cloche symétrique de Kermack et McKendrick n'est satisfaisante que si la reproductivité est inférieure à 1,5. La figure 3 compare l'expression exacte (3) du coefficient correcteur c avec les approximations (4) et (5). Avec nos valeurs numériques, ces deux dernières approximations sont indiscernables. Elles sont d'autant plus proches de la valeur exacte que la reproductivité est proche de 1. Notons qu'ici \(i/N=10^{-4}\ll (\mathbf{R_0}-1)^2=\mbox{0,04}\). La figure s'interprète comme ceci : si l'épidémie démarrait au temps 0, les valeurs des paramètres conduiraient à un pic de l'épidémie environ τ≈6,3 mois plus tard dans un environnement constant. Mais l'environnement périodique sera défavorable à ce moment car on sera dans le creux du cosinus. La taille finale de l'épidémie sera donc moindre et \(c < 0\).
On peut adapter la formule exacte (3) pour le coefficient correcteur c à des modèles plus complexes. Supposons par exemple que l'épidémie se propage entre deux populations (comme des hommes et des vecteurs) suivant le schéma S-I-R, avec \(N_1=S_1(t)+I_1(t)+R_1(t)\) et \(N_2=S_2(t)+I_2(t)+R_2(t)\) \[\frac{dS_1}{dt} = -a(t) S_1 \frac{I_2}{N_2},\quad \frac{dI_1}{dt} = a(t) S_1 \frac{I_2}{N_2} - b_1\, I_1,\quad \frac{dR_1}{dt}=b_1\, I_1\, ,\] \[\frac{dS_2}{dt} = -a(t) I_1 \frac{S_2}{N_2},\quad \frac{dI_2}{dt} = a(t) I_1 \frac{S_2}{N_2} - b_2\, I_2,\quad \frac{dR_2}{dt}=b_2\, I_2\, .\] Supposons aussi que \(a(t)=a_0(1+\varepsilon\, \phi(t))\) comme précédemment. \(S_{1,\varepsilon}(t)\), \(I_{1,\varepsilon}(t)\,\), etc., sont les solutions. Avec \(i_1=I_1(t_0)\) et \(i_2=I_2(t_0)\,\), on trouve facilement le système qui remplace l'équation (2) \[\log \frac{N_1-R_{1,\varepsilon}(\infty)}{N_1-i_1} +\frac{a_0}{b_2} \frac{R_{2,\varepsilon}(\infty)}{N_2} + \frac{a_0}{N_2}\, \varepsilon \int_{t_0}^\infty I_{2,\varepsilon}(t)\, \phi(t)\, dt=0 \] \[\log \frac{N_2-R_{2,\varepsilon}(\infty)}{N_2-i_2} +\frac{a_0}{b_1} \frac{R_{1,\varepsilon}(\infty)}{N_2} + \frac{a_0}{N_2}\, \varepsilon \int_{t_0}^\infty I_{1,\varepsilon}(t)\, \phi(t)\, dt=0 .\] Ce système a des solutions de la forme \[R_{k,\varepsilon}(\infty)=R_{k,0}(\infty)+N_k\, c_k\, \varepsilon + o(\varepsilon),\quad k\in \{1;\, 2\}.\] Avec le théorème des fonctions implicites, on a \[\left (\begin{array}{c} N_1\, c_1\\ \\ N_2\, c_2\end{array} \right ) = \left ( \begin{array}{ccc} \frac{1}{N_1-R_{1,0}(\infty)} && -\frac{a_0}{b_2 N_2} \\ && \\ -\frac{a_0}{b_1 N_2} && \frac{1}{N_2-R_{2,0}(\infty)} \end{array}\right )^{-1} \left ( \begin{array}{c} \frac{a_0}{N_2} \int_{t_0}^\infty I_{2,0}(t)\, \phi(t)\, dt\\ \\ \frac{a_0}{N_2} \int_{t_0}^\infty I_{1,0}(t)\, \phi(t)\, dt \end{array} \right ). \] Il n'est cependant pas possible de poursuivre comme dans la section 3. On n'a pas de formules approchées explicites pour \(I_{1,0}(t)\) et \(I_{2,0}(t)\).
On a déterminé de manière analytique comment la taille finale de l'épidémie était influencée par un taux de contact infectieux périodique de faible amplitude si \(\mathbf{R_0}\simeq 1\). Il s'agit d'un petit progrès par rapport aux études précédentes qui étaient soient qualitatives comme dans (Bacaër et Gomes, 2009), soit purement numériques comme dans (Bacaër et Ait Dads, 2011, figure 1). Les hypothèses sont néanmoins assez restrictives. Elles évitent en particulier les cas où plusieurs pics épidémiques se produisent. On reste proche de la situation avec un seul pic, comme dans les environnements constants. Ce sont justement ces cas qui risquent de se présenter avec l'épidémie de dengue à La Réunion.