Nicolas Bacaër
Institut de recherche pour le développement
Unité de modélisation mathématique et informatique des systèmes complexes
Les Cordeliers, Paris, France
nicolas.bacaer@ird.fr
Résumé
On aborde deux problèmes en dynamique des populations dans un environnement périodique lent ou rapide. Dans un premier temps, on obtient une approximation pour la probabilité de non-extinction d'un processus linéaire de naissance et de mort à coefficients périodiques, lorsque la période est grande ou petite. Si le taux de naissance est inférieur à la mortalité pendant une partie de la période et si la période tend vers l'infini, alors la probabilité de non-extinction converge vers une limite discontinue liée à un « canard » dans un système lent-rapide.
Dans un deuxième temps, on étudie un modèle épidémique non linéaire de type S-I-R lorsque le taux de contact oscille rapidement. La taille finale de l'épidémie est proche de celle que l'on obtient en remplaçant le taux de contact par sa moyenne. On calcule analytiquement une approximation de la correction lorsque la reproductivité de l'épidémie est proche de 1. La correction, qui peut être positive ou négative, est proportionnelle à la fois à la période des oscillations et à la fraction initiale de personnes infectées.
Dans un travail publié il y a quelque temps (Bacaër, 2015), on avait étudié la limite d'un modèle de dynamique des populations, le modèle stochastique S-I-S, dans un environnement périodique lorsque la période tendait vers 0 ou l'infini. On se propose ici d'étudier de la même manière deux modèles en apparence plus simples : un processus linéaire de naissance et de mort et un modèle épidémique déterministe de type S-I-R. Ces deux modèles peuvent être vus comme des approximations d'un même modèle S-I-R stochastique. Le processus de naissance et de mort sert d'approximation au début de l'épidémie. Les nouvelles infections jouent le rôle des naissances. Les guérisons jouent le rôle des décès. Le modèle déterministe sert d'approximation quand le nombre de personnes infectées est déjà assez grand.
Considérons donc dans un premier temps un processus linéaire de naissance et de mort dans un environnement variable avec un taux de naissance \(a(t)\) et une mortalité \(b(t)\). Le processus démarre à \(\,t=t_0\,\) avec un seul individu. La probabilité de non-extinction est \begin{equation} p(t_0)=\frac{1}{1+\int_{t_0}^\infty b(t) \exp\left [\int_{t_0}^t [b(s)-a(s)]\, ds\right ] dt}\, , \tag{1} \end{equation} que l'intégrale au dénominateur soit finie ou infinie (Gani, 1975, p. 220). Ceci s'applique en particulier au cas où les fonctions \(\,a(t)\) et \(b(t)\) sont périodiques avec la même période T. On suppose \[a(t)=A(t/T),\quad b(t)=B(t/T).\] \(A(\tau)\) et \(B(\tau)\) sont des fonctions périodiques de période 1. Considérons les moyennes \[ \bar{a}=\int_0^1 A(\tau)\, d\tau,\quad \bar{b}=\int_0^1 B(\tau)\, d\tau\, .\] \(p(t_0)\) est identiquement égal à 0 si \(\,\bar{a} \leq \bar{b}\). C'est une fonction périodique de période T, strictement positive, et strictement inférieure à 1 si \(\bar{a} > \bar{b}\,\). Voir (Bacaër, 2007, §5.2) et (Bacaër et Ait Dads, 2014). On suppose désormais \(\bar{a} > \bar{b}\). C'est le cas surcritique.
La formule (1) se simplifie lorsque la période T est soit très petite, soit très grande, comme l'a remarqué récemment (Carmona et Gandon, 2019). Avec \(\,t_0/T=\tau_0\in [0,1]\) constant et si \(T\to 0\,\), on a \(p(t_0)\approx 1-\bar{b}/\bar{a}\). Avec \(\,t_0/T=\tau_0\) constant et si \(T\to +\infty\,\), on a \(p(t_0)\approx 1-B(\tau_0)/A(\tau_0)\,\), au moins pour certaines valeurs de \(\tau_0\) avec \(A(\tau_0)>B(\tau_0)\).
L'objectif ci-dessous est de préciser ces observations en proposant une approximation de la probabilité d'extinction. La limite \(\,T\to 0\) est la plus simple : on a \begin{equation} p(t_0)=\left (1-\frac{\bar{b}}{\bar{a}}\right )\left \{1-\frac{\bar{b}\, T}{2}+\frac{T}{\bar{a}} \left [\int_0^1 \!\!\! B(\tau_0+u) \int_{\tau_0}^{\tau_0+u} \!\!\! A(v)\, dv \, du\right ] +o(T) \right \}. \tag{2} \end{equation}
Dans le cas \(T\to +\infty\,\), on suppose que les fonctions \(A(\tau)\) et \(B(\tau)\) sont régulières (disons dérivables avec une dérivée continue) et envisageons deux cas :
On montre dans la section 2 que dans le premier cas pour \(\tau_0\in [0,1]\), et dans le deuxième cas pour \(\tau_0 \not\in [\tau^*,\tau_2]\), \begin{equation} p(t_0)=\left (1-\frac{B(\tau_0)}{A(\tau_0)}\right )\left \{1 - \frac{A(\tau_0)B'(\tau_0)-A'(\tau_0)B(\tau_0)}{T A(\tau_0) [A(\tau_0)-B(\tau_0)]^2} +o(1/T)\right \}. \tag{4} \end{equation} Dans le deuxième cas avec \(\tau_0\in ]\tau^*,\tau_2[\), \begin{equation} p(t_0) \sim \frac{\sqrt{2 [A'(\tau_2)-B'(\tau_2)]}}{B(\tau_0) \sqrt{\pi T}} \, \mathrm{e}^{T\, \int_{\tau_0}^{\tau_2} [A(v)-B(v)]\, dv}\, . \tag{5} \end{equation} Cette dernière probabilité converge exponentiellement vite vers 0 quand \(T\to +\infty\). À la limite, il y a donc une discontinuité en \(\,\tau_0=\tau^*\). La limite est nulle non seulement dans \(\,]\tau_1,\tau_2[\) mais aussi dans \(]\tau^*,\tau_2[\). Ceci est lié à un phénomène de « canard » dans un système lent-rapide, comme on l'explique dans la section 2.6.
Considérons dans un deuxième temps le modèle épidémique S-I-R déterministe. On définit
Dans un travail récent (Bacaër, 2019), on s'est intéressé à l'influence qu'aurait une oscillation périodique de faible amplitude du taux de contact sur la taille finale de l'épidémie. On va s'intéresser ici au cas où l'amplitude est quelconque mais où la période des oscillations est petite par rapport à la durée typique de l'épidémie. Pour une épidémie qui durerait quelques semaines, cela représenterait par exemple l'alternance rapide entre le jour et la nuit. Pour une épidémie qui durerait quelques mois, cela représenterait l'alternance entre les jours ouvrés et les fins de semaines, notamment pour les épidémies en milieu scolaire. Pour une épidémie qui durerait plusieurs années voire plusieurs décennies, cela représenterait l'alternance entre les hivers et les étés. Il faudrait alors tenir compte des naissances et des décès.
La période des oscillations est \(T>0\). Ce paramètre est destiné à converger vers 0. On suppose que \[a(t)=\bar{a}(1+ \phi(t/T))\] avec
La section 3.1 montre des simulations de ce modèle. On constate sur des exemples que la taille finale de l'épidémie est remarquablement proche de celle que l'on obtient en remplaçant le taux de contact par sa moyenne. Dans la section 3.2, on propose une explication de cette proximité en faisant quelques hypothèses supplémentaires sur les paramètres du modèle, notamment en supposant que la fraction initiale de personnes infectées est petite et que la reproductivité de l'épidémie reste proche de 1. On obtient une formule approchée pour la correction à apporter à la taille finale de l'épidémie. Cette correction est proportionnelle à la fois à la période des oscillations et à la fraction initiale de personnes infectées, d'où sa petitesse.
Intéressons-nous tout d'abord au processus linéaire de naissance et de mort. Considérons l'intégrale au dénominateur de la formule (1) \[J=\int_{t_0}^\infty b(t) \exp\left [\int_{t_0}^t [b(s)-a(s)]\, ds\right ] dt\, .\] Par définition, on a \[ J=\int_0^\infty B((t_0+t)/T) \, \exp\left [\int_{t_0}^{t_0+t} [B(s/T)-A(s/T)]\, ds\right ] dt\, . \] On a \(t_0/T=\tau_0\). On définit \(u=t/T\) et \(v=s/T\). Alors, en utilisant la périodicité des fonctions \(\,A(\tau)\) et \(B(\tau)\), on obtient \begin{eqnarray*} J&=& T \int_0^\infty B(\tau_0+u) \, \exp\left [T \int_{\tau_0}^{\tau_0+u} [B(v)-A(v)]\, dv\right ] du\\ &=& T \sum_{n=0}^\infty \int_n^{n+1} B(\tau_0+u) \, \exp\left [T \int_{\tau_0}^{\tau_0+u} [B(v)-A(v)]\, dv\right ] du\\ &=& T \sum_{n=0}^\infty \int_0^{1} B(\tau_0+u) \, \exp\left [T \int_{\tau_0}^{\tau_0+u+n} [B(v)-A(v)]\, dv\right ] du\\ &=& T \sum_{n=0}^\infty \exp [nT(\bar{b}-\bar{a})] \int_0^{1} B(\tau_0+u) \, \exp\left [T \int_{\tau_0}^{\tau_0+u} [B(v)-A(v)]\, dv\right ] du\, . \end{eqnarray*} On a ainsi \begin{equation} J= \frac{T}{1- \exp [T(\bar{b}-\bar{a})]} \int_0^{1} B(\tau_0+u) \, \exp\left [T \int_{\tau_0}^{\tau_0+u} [B(v)-A(v)]\, dv\right ] du\, . \tag{7} \end{equation}
Avec l'approximation \(\exp(x)=1+x+x^2/2+o(x^2)\) pour \(x\to 0\) dans le facteur devant l'intégrale, et plus simplement \(\exp(x)=1+x+o(x)\) dans l'intégrale, on obtient \[ J=\left (\frac{1}{\bar{a}-\bar{b}}+\frac{T}{2}+o(T)\right )\left ( \bar{b}+T \left [\int_0^{1} B(\tau_0+u) \int_{\tau_0}^{\tau_0+u} [B(v)-A(v)]\, dv\, du\right ]+o(T) \right ).\] On a \[\int_0^{1} B(\tau_0+u) \int_{\tau_0}^{\tau_0+u} B(v)\, dv\, du = \frac{1}{2} \left [ \left (\int_{\tau_0}^{\tau_0+u} B(v)\, dv\right)^2 \,\right ]_0^1=\frac{\bar{b}^2}{2}\, .\] On en déduit que \begin{eqnarray*} J&=& \frac{\bar{b}}{\bar{a}-\bar{b}}+\frac{\bar{b}\, T}{2}+\frac{\bar{b}^2\, T}{2(\bar{a}-\bar{b})} -\frac{T}{\bar{a}-\bar{b}} \int_0^{1} B(\tau_0+u) \int_{\tau_0}^{\tau_0+u} A(v)\, dv\, du+o(T). \end{eqnarray*} Avec \(p(t_0)=1/(1+J)\,\), on en déduit la formule (2).
Reprenons la formule (7). L'intégrale est de la forme \[\int_0^1 G(u) \, \mathrm{e}^{-T\, F(u)}\, du\] avec \[G(u)=B(\tau_0+u),\quad F(u)=\int_{\tau_0}^{\tau_0+u} [A(v)-B(v)]\, dv\, .\] On a \[F'(u)=A(\tau_0+u)-B(\tau_0+u),\quad F''(u)=A'(\tau_0+u)-B'(\tau_0+u).\]
On suppose d'abord \(A(\tau)>B(\tau)\ \forall \tau \in [0,1]\). On a alors \(\,F'(u)>0\ \forall u\in [0,1]\), F atteint son minimum en \(\,u=0\) et \(F(0)=0\). De plus, \(F(u)=\phi_0\, u+\phi_1\, u^2+o(u^2)\) si \(u\to 0\,\), avec \(\phi_0=A(\tau_0)-B(\tau_0)\) et \(\phi_1=[A'(\tau_0)-B'(\tau_0)]/2\). Par ailleurs, \(G(u)=\psi_0+\psi_1\, u+o(u)\) si \(u\to 0\,\), avec \(\psi_0=B(\tau_0)\) et \(\psi_1=B'(\tau_0)\). D'après un théorème d'Erdélyi (Olver, 1974, p. 85), \begin{equation} \int_0^1 G(u) \, \mathrm{e}^{-T\, F(u)}\, du = \mathrm{e}^{-T\, F(0)} \left ( \frac{c_0}{T} + \frac{c_1}{T^2} + o\left (\frac{1}{T^2}\right ) \right ) \tag{8} \end{equation} avec \(c_0=\psi_0/\phi_0\) et \(c_1 = (\phi_0 \psi_1-2 \phi_1 \psi_0)/\phi_0^3\). Parce que \(\,\exp[T(\bar{b}-\bar{a})]\) est exponentiellement petit, la formule (7) donne \[ J = \frac{B(\tau_0)}{A(\tau_0)-B(\tau_0)} + \frac{A(\tau_0)B'(\tau_0)-A'(\tau_0)B(\tau_0)}{T [A(\tau_0)-B(\tau_0)]^3}+o(1/T). \] Avec \(p(t_0)=1/(1+J)\,\), on en déduit la formule (4).
On suppose maintenant \(\exists \, \tau_1\), \(\exists \, \tau_2\) avec \(0 < \tau_1 < \tau_2 < 1\) et
\(A(\tau) < B(\tau)\ \forall \tau\in ]\tau_1,\tau_2[\),Parce que \(\int_0^1 (A(\tau)-B(\tau)) d\tau = \bar{a}-\bar{b}>0\,\), on a deux possibilités : \begin{equation} \int_0^{\tau_2} (A(\tau)-B(\tau)) d\tau>0 \quad , \quad \int_{\tau_2}^1 (A(\tau)-B(\tau)) d\tau>0. \tag{9} \end{equation} On suppose que la première inégalité est vraie, quitte à décaler dans le temps les fonctions \(A(\tau)\) et \(B(\tau)\).
\(A(\tau)> B(\tau) \ \forall \tau \in ]0,\tau_1[ \cup ]\tau_2,1[\).
Il existe alors un unique \(\tau^*\in [0,\tau_1]\) avec \[\int_{\tau^*}^{\tau_2} (A(u)-B(u))\, du=0.\] En effet, si \[h(\tau)=\int_\tau^{\tau_2} (A(u)-B(u))\, du\, ,\quad \tau \in [0,\tau_1], \] on a \(\,h'(\tau)=B(\tau)-A(\tau) < 0\ \forall \tau \in [0,\tau_1]\). De plus, \(\,h(0)>0\) d'après la première inégalité (9) et \(h(\tau_1) < 0\). Il existe donc un unique \(\,\tau^* \in [0,\tau_1]\) avec \(h(\tau^*)=0\).
Considérons d'abord le cas où \(0 < \tau_0 < \tau_1\). La fonction \(\,F(u)\) est croissante si \(u\in [0,\tau_1-\tau_0]\). Elle est décroisssante si \(\,u\in [\tau_1-\tau_0,\tau_2-\tau_0]\). Elle est à nouveau croissante si \(\,u\in [\tau_2-\tau_0,1]\). La fonction \(\,F(u)\) a donc un minimum local en \(\tau_2-\tau_0\). On a aussi \(\,F(0)=0\).
Dans le cas \(\tau_0 \in ]0,\tau^*[\,\), on a \(F(\tau_2-\tau_0)>0\). \(\,u=0\) reste le minimum global de \(F(u)\) sur l'intervalle \([0,1]\). Le développement asymptotique (8) reste valide et la formule (4) aussi.
Si en revanche \(\tau\in ]\tau^*,\tau_1[\,\), on a \(\,F(\tau_2-\tau_0) < 0\). Le minimum global de \(\,F(u)\) sur l'intervalle \([0,1]\) est en \(u=\tau_2-\tau_0\), \(F'(\tau_2-\tau_0)=0\), \(F''(\tau_2-\tau_0)=A'(\tau_2)-B'(\tau_2)\) et \[\int_0^1 G(u) \, \mathrm{e}^{-T\, F(u)}\, du \sim \frac{B(\tau_0) \sqrt{\pi}}{\sqrt{2T [A'(\tau_2)-B'(\tau_2)]}} \, \mathrm{e}^{-T\, F(\tau_2-\tau_0)},\quad T\to +\infty, \] d'après la méthode de Laplace (Ovaert et Verley, 1997). On a ainsi \[J \sim \frac{B(\tau_0) \sqrt{\pi T}}{\sqrt{2 [A'(\tau_2)-B'(\tau_2)]}} \, \mathrm{e}^{-T\, \int_{\tau_0}^{\tau_2} [A(v)-B(v)]\, dv} \] et \(p(t_0)=1/(1+J)\sim 1/J\,\) si \(\,T\to +\infty\), ce qui donne la formule (5).
Considérons maintenant le cas où \(\tau_1 < \tau_0 < \tau_2\). \(\,F(u)\,\) est une fonction décroissante sur l'intervalle \([0,\tau_2-\tau_0]\) puis une fonction croisssante sur l'intervalle \([\tau_2-\tau_0,1]\). Son minimum dans \([0,1]\) est donc atteint en \(u=\tau_2-\tau_0\), comme dans le cas précédent. Ainsi, la formule (5) est toujours valable.
Considérons enfin le cas où \(\tau_2 < \tau_0 < 1\). \(\,F(u)\,\) est une fonction croissante sur l'intervalle \(\,[0,1+\tau_1-\tau_0]\,\) puis une fonction décroisssante sur l'intervalle \(\,[1+\tau_1-\tau_0,1+\tau_2-\tau_0]\), puis une fonction croissante sur l'intervalle \(\,[1+\tau_2-\tau_0,1]\). Cette fonction a donc un minimum local en \(\,1+\tau_2-\tau_0\) et \[F(1+\tau_2-\tau_0)\geq \int_1^{1+\tau_2} (A(\tau)-B(\tau)) \, d\tau>0\] d'après la première inégalité (9). Son minimum global dans \([0,1]\,\) est donc atteint en u=0. Ainsi, c'est la formule (4) qui s'applique.
On prend \(\,B(\tau)=\bar{b}>0\) constant et \[A(\tau)=\bar{a}(1+k\cos(2\pi \tau))\] avec \(\bar{a}>\bar{b}\) et \(0\leq k\leq 1\). Le cas fortement surcritique correspond à \(\,\bar{a}(1-k)>b\). Si au contraire \(\bar{a}(1-k) < b\,\), alors les deux solutions dans \([0,1]\) de l'équation \(\cos(2\pi\tau)=-(1-\bar{b}/\bar{a})/k\,\) sont \[\tau_1=\frac{\arccos(-(1-\bar{b}/\bar{a})/k)}{2\pi}\in ]0,1/2[,\quad \tau_2=1-\tau_1.\] Le seuil \(\tau^*\) est la solution dans \([0,\tau_1]\) de l'équation \[(\bar{a}-b)(\tau_2-\tau^*)+\bar{a}k\frac{\sin(2\pi\tau_2)-\sin(2\pi \tau^*)}{2\pi} = 0\, .\] La formule (2) donne \[p(t_0)=\left (1-\frac{\bar{b}}{\bar{a}}\right ) \left (1- \frac{\bar{b}\, k\, T}{2\pi} \sin (2\pi \tau_0)+o(T) \right ),\quad T\to 0.\] Dans le cas \(\,\bar{a}(1-k)>b\) ou dans le cas avec \(\bar{a}(1-k) < b\) et \(\tau_0\not\in [\tau^*,\tau_2]\,\), alors la formule (4) donne \[p(t_0)=\left (1-\frac{\bar{b}}{A(\tau_0)}\right ) \left (1- \frac{2\pi\, \bar{a}\, \bar{b}\, k \, \sin(2\pi \tau_0)}{T A(\tau_0) [A(\tau_0)-\bar{b}]^2} +o(1/T)\right ),\quad T\to +\infty. \] Dans le cas avec \(\,\bar{a}(1-k) < b\) et \(\tau_0\in ]\tau^*,\tau_2[\,\), La formule (5) donne \[p(t_0) \sim \frac{2\sqrt{-\bar{a} k \sin(2\pi \tau_2)}}{\bar{b} \sqrt{ T}} \exp\left [T(\bar{a}-\bar{b})(\tau_0-\tau_2)+\bar{a}kT \frac{\sin(2\pi\tau_0)-\sin(2\pi\tau_2)}{2\pi}\right ],\quad T\to +\infty.\]
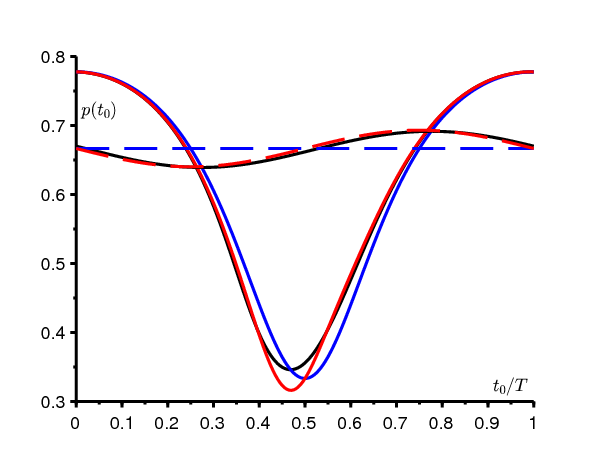
Prenons en particulier \(\bar{b}=1\), \(\bar{a}=3\) et \(k=\mbox{0,5}\). On a alors \(\, \bar{a}(1-k)>\bar{b}\). La figure 1 montre les résultats pour deux valeurs de la période : T=0,5 et T=50. La probabilité de non-extinction \(\,p(t_0)\), donnée par la formule (1), est estimée par intégration numérique avec le logiciel Scilab. On voit que les formules approchées (2) et (4) donnent de meilleures approximations. On notera cependant que pour \(\,T\to +\infty\), l'approximation (4) s'écarte un peu de \(p(t_0)\) au voisinage du minimum de \(p(t_0)\).

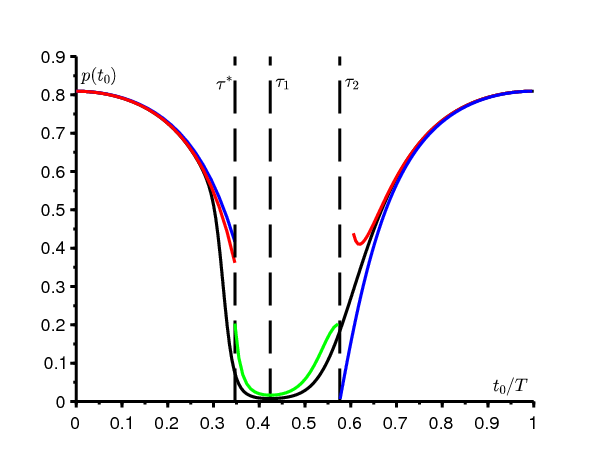
Prenons maintenant \(\bar{b}=1\), \(\bar{a}=3\), \(k=\mbox{0,75}\) et \(T=100\). On a alors \(\,\bar{a}(1-k) < \bar{b}\), \(\tau^*\simeq \mbox{0,347}\), \(\tau_1\simeq \mbox{0,424}\) et \(\tau_2\simeq \mbox{0,576}\). Les diverses formules approchées sont représentées dans la figure 2, notamment la formule (5) en vert. La probabilité de non-extinction converge vers une limite discontinue. Pour \(\,\tau < \tau^*\) et \(\tau>\tau_2\,\), la limite est en bleu. Pour \(\,\tau^* < \tau < \tau_2\,\), la limite est égale à 0. Il y a un petit problème de raccordement des approximations au niveau de \(\tau_0=\tau_2\), ce qui nous conduit à regarder de plus près ce qui se passe en ce point.
Comme dans le cas où \(\tau_2 < \tau_0 < 1\) dans la section 4.2, \(\,F(u)\,\) a son maximum global dans \([0,1]\) en \(u=0\) dans le cas spécial où \(\tau_0=\tau_2\). Mais cette fois-ci, \(\,F'(0)=A(\tau_2)-B(\tau_2)=0\). D'après le même théorème d'Erdélyi (Olver, 1974, p. 85), \[ J\sim T \int_0^1 G(u) \, \mathrm{e}^{-T\, F(u)}\, du \sim \frac{B(\tau_2) \sqrt{\pi T}}{\sqrt{2[A'(\tau_2)-B'(\tau_2)]}}\, \] de sorte que \(p(\tau_2 T)=1/(1+J)\sim 1/J\,\) si \(T\to +\infty\). La formule (5) reste valable quand \(\,\tau_0=\tau_2\). La décroissance exponentielle vers 0 lorsque \(\,\tau_0\in ]\tau^*,\tau_2[\) est remplacée par une décroissance en \(1/\sqrt{T}\) au point \(\tau_2\).
La formule (1) pour la probabilité d'extinction \(p(t_0)\) au temps \(t_0\) s'obtient en fait de la manière suivante : si \(u>t_0\,\), la probabilité d'extinction au temps u du processus qui part d'un individu au temps \(\,t_0\) est donnée par \(z(u-t_0)\) avec \(z(0)=0\) et \begin{equation} \frac{dz}{dt}=[b(u-t)-a(u-t)z(t)](1-z(t)),\quad \forall t\in [0,u-t_0] \tag{10} \end{equation} (Bacaër et Ait Dads, 2014). C'est parce que cette équation de Riccati est résoluble explicitement qu'on obtient la formule (1) pour la probabilité de non-extinction \[p(t_0)=1-\lim_{u\to +\infty} z(u-t_0).\] Prenons par exemple \(u=t_0+nT\,\) avec n entier strictement positif. L'équation (10) s'écrit alors \[\frac{dz}{dt}=\left [B \left (\frac{t_0+nT-t}{T}\right )-A\left (\frac{t_0+nT-t}{T}\right )z(t)\right ](1-z(t)).\] Avec \(s=t/T\) et \(z(t)=x(s)\,\), on a \[\frac{dx}{ds}=T \left [B(\tau_0+n-s)-A(\tau_0+n-s)x(s)\right ](1-x(s))\] sur l'intervalle \(s\in [0,n]\). Ceci peut s'écrire comme un système autonome lent-rapide : \(\,\forall s\in [0,n]\), \begin{align*} \frac{dx}{ds}&=T \left [B(\tau_0+n-y(s))-A(\tau_0+n-y(s))x(s)\right ](1-x(s)),\\ \frac{dy}{ds}&=1 \end{align*} avec \(x(0)=0\) et \(y(0)=0\). Enfin \[p(t_0)=1-\lim_{n\to +\infty} x(n).\] Avec \(T\to \infty\), on voit sur ce système lent-rapide que \(x(n)\to 1\) ou \(x(n)\to B(\tau_0)/A(\tau_0)\). Le fait que \(\,x(n)\) reste sur la branche instable \(1\) pour \(\tau^* < \tau_0 < \tau_1\,\) est donc le même phénomène que ce qui est appelé « canard » dans l'étude des systèmes lents-rapides . Rappelons la définition (Lobry, 2018, p. 182) :
« Dans un champ lent-rapide de \(\mathbb{R}^2\,\), il peut exister des trajectoires qui restent infiniment proches de la courbe lente pendant un temps significatif (non infiniment petit) le long d'un arc attractif, suivi d'un temps significatif passé le long d'un arc répulsif. Une telle trajectoire s'appelle [...] un canard. »Verhulst (2014) a également remarqué l'apparition de tels canards en lien avec une équation logistique périodique. La relation (3) qui lie \(\,\tau^*\) et \(\tau_2\) est la « relation entrée-sortie » correspondante (Benoît, 1981 ; De Maesschalck et Schecter, 2016).
Ces remarques s'étendent sans doute au cas des processus de naissance et de mort à plusieurs types (Bacaër et Ait Dads, 2014) avec des matrices de naissance \(\mathcal{A}(\tau)\) et des matrices de transition ou mort \(\mathcal{B}(\tau)\), qui conduisent à un système lent-rapide de la forme \begin{align*} \frac{dx}{ds}&=T \left [\mathcal{B}^*(\tau_0+n-y(s))-\mathrm{diag}(x(s))\, \mathcal{A}^*(\tau_0+n-y(s))\right ]\, \mathrm{colonne}(1-x(s)),\\ \frac{dy}{ds}&=1. \end{align*} \(^*\,\) désigne la matrice transposée. Dans ce cas, la relation entrée-sortie reste à déterminer.
Considérons maintenant le modèle S-I-R (6). Les paramètres sont choisis pour être plausibles :
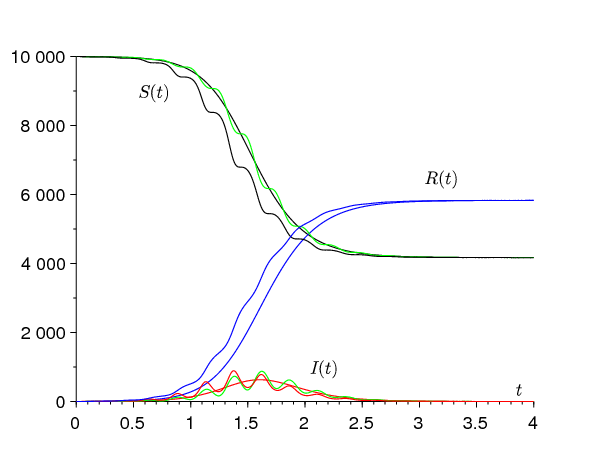
La figure 3 montre deux simulations typiques du modèle : l'une avec \(k=0\) (le taux de contact est constant), l'autre avec \(k=1\,\) (le taux de contact oscille). Quoique les courbes pour \(\,k=1\) s'éloignent notablement de celles pour \(k=0\) pendant l'épidémie, il est remarquable que les tailles finales \(R(\infty)\) dans les deux simulations soient presque indiscernables graphiquement. Ceci sera expliqué dans la section suivante.
En réduisant la période des oscillations (par exemple avec \(T=1/8\) de mois), on verrait les courbes \((S(t),I(t),R(t))\) pour \(k=1\) conserver leurs oscillations mais se rapprocher de la solution avec \(k=0\), que l'on note \((\bar{S}(t),\bar{I}(t),\bar{R}(t))\) car elle correspond à \(a(t)=\bar{a}\). C'est d'ailleurs une conséquence du théorème de moyennisation de Fatou (Françoise, 2005, théorème 42). En effet, si \(\,\tau=t/T\,\), le système s'écrit \begin{equation} \frac{dS}{d\tau}=-T\, \bar{a}(1+\phi(\tau)) \frac{S I}{N},\quad \frac{dI}{d\tau} = T\left [ \bar{a}(1+\phi(\tau)) \frac{S I}{N} - b\, I\right ],\quad \frac{dR}{d\tau}=T\, b\, I, \tag{11} \end{equation} avec \(\phi(\tau)=\cos(2\pi \tau+\psi)\). Le théorème assure que, lorsque \(\,T \to 0\), \[Z(\tau)-\bar{Z}(\tau):=(S(\tau)-\bar{S}(\tau),I(\tau)-\bar{I}(\tau),R(\tau)-\bar{R}(\tau))=O(T)\] pendant un temps \(\tau\) de l'ordre de \(1/T\). On a ainsi \(\,Z(t)-\bar{Z}(t)=O(T)\,\) pendant un temps t de l'ordre de 1. Plus précisément, il existe des constantes \(\,c_1\), \(c_2\), \(c_3\) et \(T_0\) toutes positives, avec pour \(0 < T < T_0\) et pour \(t>0\) \[\|Z(t)-\bar{Z}(t)\| \leq T \left [c_1 e^{c_2 t} + c_3\right ].\]
On peut calculer une approximation au second ordre. Écrivons le système (11) sous la forme \(\,dZ/d\tau = T f(\tau,Z)\), avec \(Z=(S,I,R)\). \(\,f(\tau,Z)\,\) est une fonction périodique de période 1 par rapport à τ. On a alors \[f_0(Z):=\int_0^1 f(\tau,Z)\, d\tau = \left (\begin{array}{c} -\bar{a}SI/N\\ \bar{a}SI/N-b\, I\\ b\, I \end{array}\right ),\] \[\int_0^\tau [f(\sigma,Z)-f_0(Z)] d\sigma = \left (\begin{array}{c} -\bar{a}\, k \frac{\sin(2\pi\tau+\psi)-\sin(\psi)}{2\pi}\, \frac{S \, I}{N}\\ \\ \bar{a}\, k\, \frac{\sin(2\pi\tau+\psi)-\sin(\psi)}{2\pi}\, \frac{S \, I}{N}\\ \\ 0\end{array}\right ).\] Il faut retrancher l'expression en \(\sin(\psi)\,\) pour que ces dernières fonctions soient de moyenne nulle. D'après (Françoise, 2005, théorème 44), on a \[S(\tau)= \bar{S}(\tau)-T \, \frac{\bar{a}\, k\, \sin(2\pi\tau+\psi)}{2\pi}\, \frac{\bar{S}(\tau) \, \bar{I}(\tau)}{N}+O(T^2),\] \[ I(\tau)= \bar{I}(\tau)+T \, \frac{\bar{a}\, k\, \sin(2\pi\tau+\psi)}{2\pi}\, \frac{\bar{S}(\tau) \, \bar{I}(\tau)}{N}+O(T^2)\] et \(R(\tau) = \bar{R}(\tau)+O(T^2)\) sur un intervalle de temps \(\tau\) de l'ordre de \(1/T\). Autrement dit, \[S(t)= \bar{S}(t)-\frac{\bar{a}\, k\, \sin(\omega t+\psi)}{\omega}\, \frac{\bar{S}(t) \, \bar{I}(t)}{N}+O(1/\omega^2),\] \[ I(t)= \bar{I}(t)+\frac{\bar{a}\, k \, \sin(\omega t+\psi )}{\omega}\, \frac{\bar{S}(t) \, \bar{I}(t)}{N}+O(1/\omega^2)\] et \(R(t) = \bar{R}(t)+O(1/\omega^2)\) sur un intervalle de temps \(t\) de l'ordre de \(1\). Ces approximations de \(\,S(t)\) et \(I(t)\) sont représentées en vert dans la figure 3.
Remarquons qu'avec une période du taux de contact qui est petite, on n'observe pas de courbe épidémique avec plusieurs grandes vagues, contrairement aux simulations de (Bacaër et Gomes, 2009). C'est que le système se rapproche de plus en plus du cas où le taux de contact est moyenné, qui ne donne qu'une seule vague épidémique.
En écrivant la première équation (6) sous la forme \( \frac{d}{dt}(\log S)= -a(t) I/N\,\), en intégrant entre \(t=0\) et \(t=+\infty\,\), en tenant compte des conditions initiales et de \(\int_0^\infty I(t)\, dt = R(\infty)/b\), on trouve facilement comme dans (Bacaër, 2019) que \begin{equation} \log \frac{N-R(\infty)}{N-i} +\frac{\bar{a}}{b} \frac{R(\infty)}{N} + \frac{\bar{a}}{N} \int_{0}^\infty I(t)\, \phi(t/T)\, dt=0\, . \tag{12} \end{equation} L'intégrale oscillante \(\int_{0}^\infty I(t)\, \phi(t/T)\, dt\) converge sans doute vers 0 quand \(T \to 0\). En effet, on sait d'une part que \(\,I(t)\simeq \bar{I}(t)\). D'autre part, du moins lorsque \(\,\phi\) est un cosinus, l'intégrale \(\int_{0}^\infty \bar{I}(t)\, \phi(t/T)\, dt\) converge vers 0 quand \(T \to 0\). En effet, la fonction \(\,\bar{I}(t)\) est positive et intégrable, car \(\int_0^\infty \bar{I}(t)\, dt = \bar{R}(\infty)/b\). La transformée de Fourier d'une fonction intégrable converge vers 0 à l'infini.
Il en résulte que \(R(\infty)\to \bar{R}(\infty)\) si \(T \to 0\). La question est de savoir à quelle vitesse ceci se produit. En première approximation, l'équation (12) donne \[R(\infty)\simeq \bar{R}(\infty)+ \frac{\bar{a} }{N/(N-\bar{R}(\infty))-\bar{a}/b} \, \int_{0}^\infty \bar{I}(t)\, \phi(t/T)\, dt\, \] comme dans (Bacaër, 2019).
Puis on utilise pour \(\bar{I}(t)\,\) l'expression analytique approchée en forme de cloche symétrique obtenue par Kermack et McKendrick (voir par exemple (Bacaër, 2019) ou (Gani, 1975)). Avec \(\bar{a}/b>1\,\), \(\bar{a}/b \simeq 1\,\) et \(i/N \ll 1\,\), on a \begin{equation} \bar{I}(t) \simeq \frac{N\, X}{\mathrm{ch}^2[Y (t-W)]}\, . \tag{13} \end{equation} \(\mathrm{ch}(\cdot)\) désigne le cosinus hyperbolique et \begin{equation} W \simeq \frac{\log\left [2(N/i)(1-b/\bar{a})^2\right ]}{\bar{a}-b},\quad X\simeq \frac{(1-b/\bar{a})^2}{2},\quad Y\simeq \frac{\bar{a}-b}{2} \tag{14} \end{equation} sous l'hypothèse supplémentaire vraisemblable \(i/N \ll (\bar{a}/b-1)^2\). \(W\) est une approximation du temps qui s'écoule avant le pic de l'épidémie dans un environnement constant.
Supposons enfin que \(\phi(\tau)=k \cos(2\pi \tau+\psi)\) comme dans la figure 3. Notons \(\mathrm{Re}(\cdot)\) la partie réelle d'un nombre complexe et \(\mathrm{i}\) le nombre imaginaire habituel (à ne pas confondre avec \(i\,\), la population infectée initialement). On a alors, en utilisant un résultat classique sur le calcul asymptotique des intégrales complexes avec une phase qui n'est pas stationnaire de sorte que le terme principal vient du bord de l'intervalle d'intégration (Ovaert et Verley, 1997, théorème 3), \begin{eqnarray*} \int_{0}^\infty \bar{I}(t)\, \phi(t/T)\, dt& \simeq & N\, X\, k \int_{0}^\infty \frac{\cos(\omega t+\psi)}{\mathrm{ch}^2[Y (t-W)]}\, dt \\ &= & N\, X\, k\ \mathrm{Re}\left (\mathrm{e}^{\mathrm{i}\psi} \int_{0}^\infty \frac{\mathrm{e}^{\mathrm{i}\omega t}}{\mathrm{ch}^2[Y (t-W)]}\, dt \right ) \\ & \simeq & - N\, X\, k\, \mathrm{Re}\left (\frac{\mathrm{e}^{\mathrm{i}\psi}}{\mathrm{i}\, \omega\, \mathrm{ch}^2(-Y W)}\right )\\ &=& - \frac{N\,X\, k\, \sin(\psi)}{\omega \, \mathrm{ch}^2(Y W)}\, . \end{eqnarray*} Avec les approximations (14), on voit en plus que \[\mathrm{ch}^2(Y W) \simeq \mathrm{e}^{2YW}/4 \simeq (N/i) (1-b/\bar{a})^2/2\simeq (N/i) X,\] ce qui donne finalement pour \(\omega \to +\infty\) \begin{equation} R(\infty)\simeq \bar{R}(\infty)- \frac{\bar{a}\, k\, \sin(\psi) }{N/(N-\bar{R}(\infty))-\bar{a}/b}\ \frac{i\, }{ \omega}\, \, . \tag{15} \end{equation}
La taille finale \(\bar{R}(\infty)\) dans un environnement constant est l'unique solution strictement positive de l'équation \[1-\frac{\bar{R}(\infty)}{N}=(1-i/N)\exp \left (-\frac{\bar{a}}{b} \frac{\bar{R}(\infty)}{N}\right ),\] ce que l'on retrouve facilement à partir de l'équation (12). Avec \(\,i\ll N\), la taille finale \(\bar{R}(\infty)\) ne dépend que très peu de la condition initiale \(i\). C'est de manière approchée la solution strictement positive de \[1-\frac{\bar{R}(\infty)}{N}\simeq \exp \left (-\frac{\bar{a}}{b} \frac{\bar{R}(\infty)}{N}\right ).\] Le terme correcteur dans l'équation (15) peut être positif ou négatif ; cela dépend du signe de \(\,\sin(\psi)\). Il est à la fois proportionnel à \(\, 1/\omega\), c'est-à-dire à T, et à la fraction i/N de personnes initialement infectées. C'est pourquoi, comme annoncé, la taille finale de l'épidémie est remarquablement proche de celle que l'on obtient en remplaçant le taux de contact par sa moyenne.
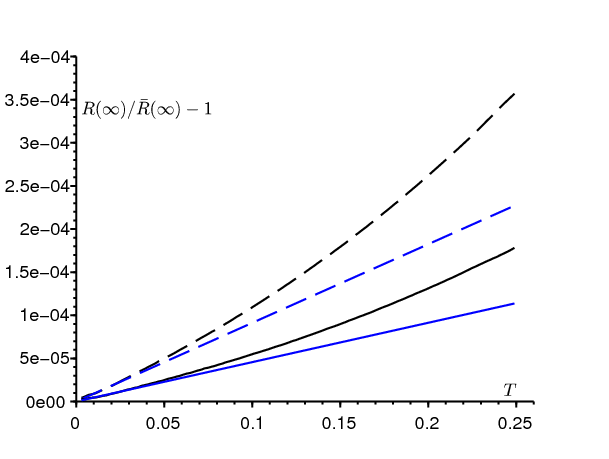
Ceci est illustré dans la figure 4 avec des valeurs des paramètres identiques à celles de la figure 3 pour k=1. La période T varie. On a aussi essayé deux conditions initiales : \(\,i=1\) et \(i=2\). La courbe pour \(\,R(\infty)\,\) est tangente à l'approximation (15) si \(\,T\to 0\). On remarque sur l'échelle verticale la petitesse de la différence relative \(\,[R(\infty)-\bar{R}(\infty)]/\bar{R}(\infty)\). Avec N=10000, cela se traduit pour la taille finale de l'épidémie au maximum par une différence de 1 ou 2 personnes (la taille devrait en principe être un nombre entier). Avec \(\,\bar{a}/b=\mbox{1,5}\,\), l'approximation (13) de Kermack et McKendrick est encore relativement bonne (Gani, 1975, p. 240).
Si ψ est nul ou un multiple entier du nombre π, le terme correcteur dans l'équation (15) est nul. Mais comme il s'agit d'un cas exceptionnel, il ne vaut peut-être pas la peine de trouver un nouvel équivalent pour l'intégrale \(\,\int_{0}^\infty \bar{I}(t)\, \phi(t/T)\, dt\) ci-dessus.
En conclusion, on peut dire que la proximité des tailles finales \(R(\infty)\) et \(\bar{R}(\infty)\) justifie d'une certaine manière le fait que dans beaucoup de modèles épidémiques, on néglige les oscillations de courte période pour ne considérer que des taux de contacts moyens.