Le pic épidémique dans un modèle S-I-R

Résumé

On étudie une épidémie modélisée par un système différentiel de type S-I-R. Lorsque la population N est grande, le pic épidémique est au temps T, avec \(\,T\sim (\ln N)/(a-b)\).  \(\,a\)  est le taux de contact effectif.  \(\,b\) est le taux auquel les personnes infectieuses guérissent.

Introduction

    Considérons comme par exemple dans [1, 2, 6, 7, 8] le modèle S-I-R de Kermack et McKendrick pour une épidémie \[\frac{dS}{dt} = -a \frac{S I}{N},\quad \frac{dI}{dt} = a \frac{S I}{N} - b I,\quad \frac{dR}{dt}=b I.\] \(S(t)\) est le nombre de personnes saines. \(I(t)\) est le nombre de personnes infectées. \(R(t)\) est le nombre de personnes retirées de la transmission par suite d'un isolement, d'une guérison ou d'un décès. \(N=S(t)+I(t)+R(t)\,\) est la population totale. Cette population totale est supposée constante et suffisamment grande pour qu'il soit raisonnable de modéliser l'épidémie par un système différentiel plutôt que par un processus stochastique. Considérons les conditions initiales \[S(0)=N-1,\quad I(0)=1,\quad R(0)=0,\] qui correspondent au démarrage de l'épidémie à partir d'un seul « patient zéro ».

    Le paramètre \(a\) (avec \(a > 0\)) est en fait le produit de deux nombres : le nombre de contacts par unité de temps et la probabilité de transmission lors d'un contact entre une personne non infectée et une personne infectée. Les contacts ont lieu au hasard. \(\,I/N\,\) est la probabilité pour une personne d'être dans le compartiment I. Ceci explique le terme quadratique en \(\,SI/N\,\) dans le système différentiel. \(\,b>0\,\) est le taux auquel les personnes quittent le compartiment I. L'hypothèse sous-jacente est donc que le temps passé dans le compartiment I est distribué selon une loi exponentielle de paramètre b. On supposera a>b pour qu'une véritable épidémie ait lieu.

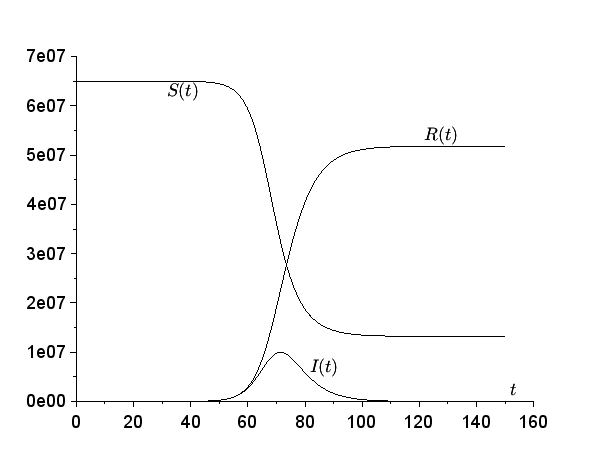
    Un exemple est détaillé à la figure 1. On a utilisé le logiciel Scilab et sa fonction de résolution des systèmes différentiels. Cette fonction implémente un schéma prédicteur-correcteur d'Adams pour les systèmes qui ne sont pas raides. On a choisi \(\,N=65\times 10^6\) (la population de la France),  \(a=1/2\) par jour et \(b=1/4\,\) par jour. Au début de l'épidémie, une personne infectée infecte donc en moyenne une personne tous les deux jours. La durée moyenne d'infection \(\,1/b\,\) est de 4 jours. Cela correspond à une reproductivité \(\,\mathcal{R}_0=a/b=2\,\) (le terme et la notation proviennent de [9, p. 102]). \(\,\mathcal{R}_0\,\) est donc le nombre moyen de cas secondaires qu'une personne infectée infecte au début de l'épidémie. Sans prétendre être réaliste, il s'agit de valeurs du même ordre de grandeur que ce qu'on peut trouver pour l'épidémie de coronavirus de 2020 dans le cas hypothétique où il n'y aurait aucune intervention pour limiter l'épidémie [5].

Le pic épidémique

    En combinant la première et la troisième équation du système S-I-R, il est bien connu [8, p. 76] qu'on trouve une intégrale première : \[ \frac{1}{S} \frac{dS}{dt} = -a\, \frac{I}{N} = - \frac{a}{bN} \frac{dR}{dt}. \] On a donc \[\ln [S(t)/S(0)] = -\frac{a}{bN} R(t).\] En reportant dans la première équation, on trouve \[\frac{dS}{dt}=-a \frac{S}{N} (N-S-R) =-a \frac{S}{N} \left (N-S+\frac{bN}{a} \ln [S(t)/S(0)]\right ).\] Le pic épidémique de la figure 1 correspond à \(dI/dt=0\), ce qui arrrive d'après la deuxième équation quand \(S(t)=Nb/a\). \(\,S(t)\) est une fonction décroissante parce que \(dS/dt \leq 0\,\) d'après la première équation. On en déduit que si T est l'instant du pic épidémique, c'est-à-dire si \[I(T)=\max_{t>0} I(t),\] on a alors \[T=\int_0^T dt = \int_{S(0)}^{bN/a} \frac{dS}{-a \frac{S}{N} \left (N-S+\frac{bN}{a} \ln [S/S(0)]\right )}.\] On définit \(s=S/N\). On a alors \begin{equation}\tag{1} T=\frac{1}{a} \int_{b/a}^{1-1/N} \frac{ds}{ s \left (1-s+\frac{b}{a} \ln [s/(1-1/N)]\right )}. \end{equation}

    On cherche un majorant de T. Pour tout \(\ b/a < s < 1-1/N\), on a \[\frac{1}{s \left (1-s+\frac{b}{a} \ln [s/(1-1/N)] \right )}\leq \frac{1}{s \left (1-s+\frac{b}{a} \ln s \right )}.\] Au voisinage de \(s=1\), on a \[ \frac{1}{s \left (1-s+\frac{b}{a} \ln s \right )} \sim \frac{1}{(1-s)(1-b/a)}\, .\] L'intégrale \[\int_{b/a}^1 \frac{ds}{1-s}\] est divergente. Avec \(\,N\to +\infty\), on obtient \[T \leq \frac{1}{a} \int_{b/a}^{1-1/N} \frac{ds}{s \left (1-s+\frac{b}{a} \ln s \right )} \sim \frac{1}{a} \int_{b/a}^{1-1/N} \frac{ds}{(1-s)(1-b/a)}\sim \frac{\ln N}{a-b}\, .\]

    On cherche un minorant de T. On a \(\ln s \leq s-1\) pour tout  \(\,s > 0\,\). On a par ailleurs \(\,\ln(1-1/N) \geq -2/N\) pour tout entier \(N\geq 2\). On a donc pour \(\,s\in ]b/a,1-1/N[\,\) et pour tout nombre entier N≥2, \begin{eqnarray*} 1-s+\frac{b}{a} \ln [s/(1-1/N)] &=& 1-s+\frac{b}{a} \ln s - \frac{b}{a} \ln(1-1/N)\\ &\leq& 1-s+\frac{b}{a}(s-1)+\frac{2b}{aN}. \end{eqnarray*} On a donc \[T\geq \frac{1}{a} \int_{b/a}^{1-1/N} \frac{ds}{s[1-\frac{b}{a}+\frac{2b}{aN}-(1-b/a)s]}. \] On tombe sur une fraction rationnelle de la forme \(\frac{1}{s(u-vs)}\) avec \[u=1-\frac{b}{a}+\frac{2b}{aN},\quad v=1-b/a.\] Elle se décompose en éléments simples \[\frac{1}{s(u-vs)}=\frac{1}{u} \left (\frac{1}{s}+\frac{v}{u-vs} \right ).\] Une primitive est \[\frac{1}{u} [\ln s - \ln(u-vs)]=\frac{1}{u} \ln \frac{s}{u-vs}.\] On a donc \begin{eqnarray*} T &\geq& \frac{1}{a(1-\frac{b}{a}+\frac{2b}{aN})} \ln \left \{ \frac{1-1/N}{b/a} \ \frac{1-\frac{b}{a}+\frac{2b}{aN} - (1-b/a)b/a}{1-\frac{b}{a}+\frac{2b}{aN} - (1-b/a)(1-1/N)} \right \}\\ &=&\frac{1}{a-b+2b/N} \ln \left \{\frac{1-1/N}{b/a} \ \frac{(1-b/a)^2+\frac{2b}{aN} }{(1+b/a)/N} \right \}\\ &=&\frac{1}{a-b+2b/N} \left [\ln N + \ln \left \{\frac{1-1/N}{b/a} \ \frac{(1-b/a)^2+\frac{2b}{aN} }{(1+b/a)} \right \} \right ]. \end{eqnarray*} Le membre de droite est  \(\sim (\ln N)/(a-b)\)  si  \(N\to +\infty\). Comme c'est le même équivalent que celui du majorant obtenu ci-dessus, on en conclut que \(T\sim (\ln N)/(a-b)\)  si  \(N\to +\infty\).

    Dans l'exemple de la figure 1, on a  \(T\simeq \mbox{71,4}\)  jours tandis que  \((\ln N)/(a-b)\simeq \mbox{72,0}\,\) jours. L'approximation semble assez bonne. Dans la figure 2, on fait varier la taille N de la population ainsi que le paramètre \(\,a\,\), avec b fixé. On remarque \((\ln N)/(a-b)\,\) tantôt surestime, tantôt sous-estime T.

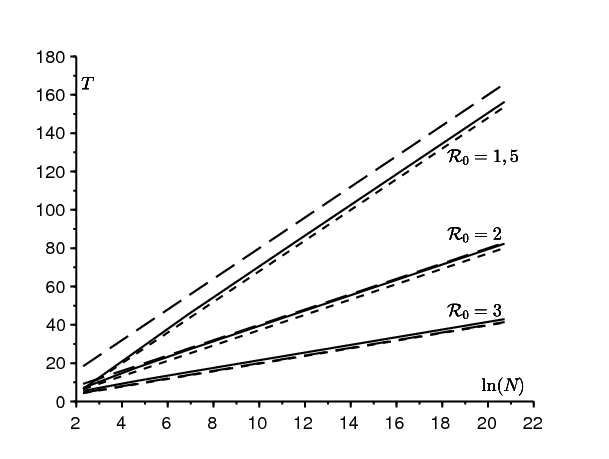
    \(a-b\,\) est le taux de croissance initial de l'épidémie. On a alors pour N grand, \(\,S(t)\simeq N\)  et  \(dI/dt \simeq (a-b)I\). Ce taux peut être estimé à partir des données épidémiologiques. La population N est connue. On peut donc prévoir la date du pic de l'épidémie. En pratique, l'hypothèse sous-jacente au modèle d'un mélange homogène de la population reste néanmoins douteuse pour un pays entier, un peu moins pour une ville.

    Historiquement, Kermack et McKendrick avaient résolu de manière approchée le système S-I-R en supposant que la reproductivité était proche de 1, ce qui conduit à une petite épidémie. Avec l'approximation \(\,e^{x}\simeq 1+x+x^2/2\,\), ils étaient parvenus à une équation de Riccati résoluble explicitement, de sorte que \begin{equation}\tag{2} I(t)\simeq \frac{X}{\mathrm{ch}^2(Yt-Z)}. \end{equation} X, Y et Z sont des fonctions compliquées des paramètres N, a et b. Voir par exemple [3]. Le pic épidémique est \(\,T \simeq Z/Y\). Notons au passage qu'à notre connaissance l'approximation (2) n'a jamais été démontrée rigoureusement, ce pourquoi on utilise ci-dessus et ci-dessous le signe informel \(\simeq\). On suppose maintenant en plus \(1/N\ll (\mathcal{R}_0-1)^2\). Dans ce cas, \[Y\simeq \frac{a-b}{2},\quad Z\simeq \frac{1}{2} \ln [2N(b/a-1)^2]\] (voir par exemple [4]), de sorte que \[T \simeq \frac{\ln [2N(b/a-1)^2]}{a-b}\, .\] Cette approximation est également représentée dans la figure 2 ; elle semble particulièrement proche de la vraie valeur de T si \(\,\mathcal{R}_0\,\) est proche de 1, comme on pourrait s'y attendre. Avec N qui converge vers l'infini, on a néanmoins \(T \simeq \frac{\ln N}{a-b}\,\). On retrouve le même comportement asymptotique. Notre analyse basée sur la formule (1) est valable cependant pour tout \(\,\mathcal{R}_0 > 1\)  et pas seulement pour  \(\mathcal{R}_0\,\) proche de 1. De plus, notre preuve est rigoureuse.

Conclusion

    On a trouvé que le pic de l'épidémie avait lieu à un temps \(T \sim (\ln N)/(a-b)\)  si N converge vers l'infini. Ce résultat semble nouveau malgré sa simplicité. Dans la littérature scientifique, on n'a trouvé que des informations sur la hauteur du pic, qui se détermine facilement grâce à l'intégrale première du système. En effet, Avec \[S(T)=\frac{N\, b}{a},\quad \ln \frac{S(T)}{S(0)} = -\frac{a}{bN} R(T),\quad N=S(T)+I(T)+R(T),\] on obtient \[\frac{I(T)}{N}=1-\frac{b}{a}+\frac{b}{a} \ln \left (\frac{N}{N-1}\ \frac{b}{a} \right ) \simeq 1-\frac{b}{a}+\frac{b}{a} \ln \frac{b}{a}\] (voir par exemple [1, équation 7.26]). Dans certaines références comme [7, p. 238], il y a des inversions où le temps t est une fonction des variables monotones R ou S, ce qui conduit à des intégrales comme (1) à un changement de variable près. Mais le système différentiel S-I-R y était écrit sous la forme \(\,dS/dt = - \alpha S I\,\). L'idée n'était probablement pas venue de prendre \(\,\alpha = a/N\), ce qui est d'une certaine manière plus réaliste et nécessaire pour que la limite d'une grande population donne des résultats intéressants.

    Pour une épidémie comme celle de coronavirus, le modèle S-I-R manque un peu de réalisme. Cela conduit à considérer des modèles avec plus de compartiments, par exemple avec un compartiment supplémentaire pour les personnes dans la phase latente qui sont infectées mais pas encore contagieuses. Voir à ce sujet [5], qui essaie aussi d'estimer les paramètres à partir de la courbe épidémique. L'étude analytique du pic épidémique dans ce cadre-là est sans doute plus difficile.

Remerciements

    On remercie Hisashi Inaba pour ses commentaires sur le texte.

Références bibliographiques