Un modèle mathématique pour une transition démographique partielle

Résumé

On étudie un modèle mathématique pour la transition démographique. Il y a deux classes d'âge et deux niveaux de fécondité. Les adultes avec une fécondité élevée imitent les adultes avec une fécondité faible. Lorsque le coefficient d'imitation augmente, la population traverse deux seuils entre lesquels la population croît ou décroît exponentiellement avec un mélange stable des deux fécondités. Cette transition démographique partielle rappelle la situation dans certains pays d'Afrique subsaharienne.

Mots-clés : modèle mathématique, transition démographique, croissance exponentielle

1     Introduction

    La transition démographique est un phénomène qui s'étend sur des décennies. La population voit d'abord sa mortalité baisser. Puis, avec un certain retard, la fécondité baisse aussi. À cause de ce décalage, la population croît souvent de manière considérable, avec d'importantes conséquences économiques et sociales [3].

    L'hypothèse bien connue de la modernisation insiste sur le fait que le faible taux de fécondité est le résultat d'une adaptation individuelle à des environnements modernisés : industrialisation, urbanisation, changements de normes éducatives et familiales. Il est néanmoins difficile d'établir un lien direct entre la baisse de la fécondité et de nombreux indices du niveau de développement social. On cherche par conséquent un mécanisme dynamique pour comprendre l'écart entre le changement d'attitude individuel et les données statistiques macroscopiques.

    Si l'on suit le découpage en « trois démographies » de [9], on peut dire que la transition démographique peut être envisagée sous trois angles : statistique, politique ou mathématique. C'est sous ce dernier angle, illustré notamment par les travaux de Verhulst ou de Lotka [19, 12] et résumé par exemple par [14], que l'on va considérer le problème.

    Du point de vue de la modélisation mathématique, la transition démographique peut être présentée soit comme exogène, soit comme endogène. Dans le premier cas, la population est supposée homogène mais la modernisation des conditions de vie fait que les paramètres démographiques varient dans le temps. Cela conduit à des modèles non autonomes [1].

    L'approche endogène consiste au contraire à utiliser des modèles autonomes, c'est-à-dire dont les coefficients ne dépendent pas du temps, avec une population hétérogène. Les changements qualitatifs résultent alors de l'interaction entre les sous-populations. La transition démographique est un peu analogue à une épidémie. Des normes culturelles novatrices qui réduisent le nombre de naissances peuvent être transmises par des individus à faible fécondité (les « infectés ») à des individus traditionnels à fécondité élevée (les personnes « saines »), comme dans la théorie de la diffusion [18, 13]. Ce processus de transmission peut être déclenché par des changements socio-économiques et environnementaux.

    [8] a récemment développé ce point de vue épidémique pour la théorie de la diffusion de la transition de la fécondité. Le déclin de la fécondité est décrit comme le résultat de la diffusion de la tendance à avoir moins d'enfants. Leur premier modèle divisait la population entre individus avec une fécondité élevée et individus avec une fécondité faible, \(\,P_1(t)\) et \(P_2(t)\). Leurs nombres évoluaient selon un système différentiel homogène de degré un \begin{equation*} \frac{dP_1}{dt}=r_1\, P_1-b\, \frac{P_1\, P_2}{P_1+P_2}\, , \quad \frac{dP_2}{dt}=r_2\, P_2+b \, \frac{P_1\, P_2}{P_1+P_2}\, . \end{equation*} \(r_1\) et \(r_2\) sont les taux de croissance des populations isolées, avec \(r_1 > r_2\). \(\,b\,\) est un coefficient d'imitation indiquant le taux maximum auquel les individus avec une fécondité élevée adoptent une fécondité faible. Ce taux est supposé dépendre linéairement de la fraction de la population avec une fécondité faible : \(\,f(t)=P_2(t)/(P_1(t)+P_2(t))\). En termes écologiques, c'est un système proies-prédateurs à la manière de Lotka et Volterra [20] mais avec un taux de prédation non linéaire qui ne dépend que du rapport des deux populations, comme dans le modèle d'Arditi et Ginzburg [11, § 2.3]. L'analyse mathématique est très simple. Il suffit d'observer que \(\,f(t)\) est solution d'une équation logistique. Selon que \(\,b < r_1-r_2\) ou \(b > r_1-r_2\,\), la population totale tend à croître exponentiellement avec un taux \(r_1\) ou \(r_2\,\) et c'est la fraction de la population avec une fécondité faible ou celle avec une fécondité élevée qui converge vers 0. En partant d'une population avec une fécondité élevée et quelques individus avec une fécondité faible, la transition démographique a donc lieu si et seulement si \(\,b > r_1-r_2\).

    Dans un deuxième temps, [8] étudie une version structurée par âge du même modèle. Comme l'âge x était une variable continue, cela conduisait à un système d'équations aux dérivées partielles du type de McKendrick et von Foerster : \begin{eqnarray*} \frac{\partial P_1(t,x)}{\partial t}+\frac{\partial P_1(t,x)}{\partial x}&=&-m(x) P_1(t,x) -\pi(t,x) P_1(t,x),\\ \frac{\partial P_2(t,x)}{\partial t}+\frac{\partial P_2(t,x)}{\partial x}&=&-m(x)P_2(t,x)+\pi(t,x)P_1(t,x),\\ P_1(t,0)&=&\int_{0}^{\infty}a_1(x)\, P_1(t,x)\, dx,\\ P_2(t,0)&=&\int_{0}^{\infty}a_2(x)\, P_2(t,x)\, dx, \end{eqnarray*} avec \[ \pi(t,x):=\frac{\int_{0}^{\infty}b(x,y)\, P_2(t,y)\, dy}{\int_{0}^{\infty}[P_1(t,y)+P_2(t,y)]\, dy}. \] Dans ce modèle, \(m(x)\) est le taux de mortalité, \(a_1(x)\) et \(a_2(x)\,\) sont les taux de fertilité. L'analyse mathématique du modèle est alors plus compliquée et seuls des résultats très partiels ont été obtenus. Il n'existe en général plus un seul seuil mais deux. Sous le premier seuil et au-dessus du second seuil, il existe une unique solution exponentielle triviale localement stable (au sens de la théorie des systèmes homogènes) composée d'individus avec une fécondité élevée dans le premier cas, avec une fécondité faible dans le second cas. Entre les deux seuils, au moins pour certaines valeurs des paramètres (c'est-à-dire avec certaines conditions supplémentaires certainement non optimales), il a été possible de prouver l'existence d'une solution exponentielle non triviale avec des individus qui ont des fécondités différentes. L'unicité et la stabilité de cette solution non triviale n'ont pas été abordées. Pour cette solution, le taux de croissance de la population est intermédiaire entre les deux cas extrêmes. Il y a une transition démographique partielle. Cette différence qualitative avec le premier modèle n'était pas évidente a priori.

    Le régime entre les deux seuils semblait anecdotique dans [8], puisque la motivation provenait de la démographie du Japon. La transition démographique y est si avancée que le taux de croissance de la population est devenu négatif. On se trouve au-delà du second seuil. En revanche, il se pourrait que le régime intermédiaire présente un intérêt dans le cas de certains pays d'Afrique subsaharienne. La fécondité moyenne y a effectivement baissé un peu mais bien moins que ce que prévoyaient les démographes [10]. Par ailleurs, les difficultés d'analyse du système d'équations aux dérivées partielles poussent à chercher un modèle plus simple pour une transition démographique partielle.

    On étudie donc ci-dessous un modèle avec seulement deux classes d'âge (jeunes et adultes) au lieu d'un âge qui varie continûment. L'intérêt est qu'il conserve le même phénomène de transition à deux seuils. Ceci permet de faire une étude plus complète. On montre notamment que la solution non triviale est unique et que son domaine d'existence coïncide exactement avec le domaine d'instabilité des solutions triviales. On parvient aussi à prouver la stabilité locale de la solution non triviale.

    On présente le modèle dans la section 2 avec ses solutions exponentielles triviales et non triviales. On étudie la stabilité des solutions exponentielles dans la section 3 en utilisant notamment le critère de Routh-Hurwitz et la théorie des systèmes différentiels homogènes de degré un. Pour cette théorie, voir [6, p. 638] et les livres [5, chap. 5], [7, chap. 4] et [16, chap. 4]. Comme le système est de dimension 4, la stabilité de la solution exponentielle non triviale présente une difficulté qui était absente des exemples des références ci-dessus, et qui a nécessité l'utilisation d'un logiciel de calcul formel. La section 4 présente un exemple numérique qui se veut représentatif de quelques pays d'Afrique subsaharienne. La section 5 propose une conjecture pour le comportement asymptotique global faute d'avoir trouvé une fonction de Liapounov convenable. Quoique plus simple que celle du système d'équations aux dérivées partielles, l'analyse de notre modèle est donc encore incomplète.

2     Le modèle et ses solutions exponentielles

    On définit

• \(X_1(t)\) le nombre de jeunes de familles fécondes
• \(Y_1(t)\) le nombre d'adultes de familles fécondes
• \(X_2(t)\) le nombre de jeunes de familles avec une fécondité réduite
• \(Y_2(t)\) le nombre d'adultes de familles avec une fécondité réduite.

    On définit \(\,Z=(X_1,Y_1,X_2,Y_2)\,\). Le système différentiel ci-dessus peut s'écrire sous la forme suivante \begin{equation} \frac{dZ}{dt}=F(Z) \tag{3} \end{equation} avec une fonction F qui est une fonction vectorielle homogène de degré un. L'existence globale et la positivité des solutions du système (3) se montrent comme dans les modèles démographiques avec mariage. Voir par exemple [16, chap. 4]. La positivité résulte de ce que \(\,dX_1/dt\geq 0\) si \(X_1=0\), \(dY_1/dt\geq 0\) si \(Y_1=0\), etc. Avec une condition initiale dont les composantes sont toutes strictement positives, chaque composante reste même strictement positive pour tout t>0. L'existence globale résulte de l'inégalité à laquelle obéit la population totale \[P=X_1+Y_1+X_2+Y_2,\quad \frac{dP}{dt} \leq (a_1-m) P.\]

    \(Z(t)= e^{\lambda t} z\) est une « solution exponentielle positive » du système (3) si

• \(z=(z_i)\) est un vecteur avec \(z_i\geq 0\, \forall \, i\)
• \(\sum_i z_i > 0\)
• \((\lambda,z)\) est une solution du problème de valeur propre non linéaire \(\lambda z=F(z).\)

Proposition 1 . Il existe une unique solution exponentielle positive normalisée de la forme \(\,e^{\lambda_1 t} (x_1,y_1,0,0)\) \[\lambda_1= \frac{ -c+ \sqrt{c^2+4a_1 c} }{2}-m,\quad x_1=\frac{-c+\sqrt{c^2+4a_1 c}}{c+\sqrt{c^2+4a_1 c}},\quad y_1=\frac{2c}{c+\sqrt{c^2+4a_1 c}} .\] De même, il existe une unique solution exponentielle positive normalisée de la forme \(e^{\lambda_2 t} (0,0,x_2,y_2)\) \[\lambda_2= \frac{ -c+ \sqrt{c^2+4a_2 c} }{2}-m,\quad x_2=\frac{-c+\sqrt{c^2+4a_2 c}}{c+\sqrt{c^2+4a_2 c}},\quad y_2=\frac{2c}{c+\sqrt{c^2+4a_2 c}} .\] Dans le cas \(\,b_1 < b < b_2\) avec \[ b_1=\frac{2(a_1-a_2)}{1+\sqrt{1+4a_1/c}}, \quad b_2=\frac{2(a_1-a_2)}{1+\sqrt{1+4a_2/c}},\] alors il existe une unique solution exponentielle positive normalisée de la forme \(e^{\lambda^* t}(x_1^*,y_2^*,x_2^*,y_2^*)\) avec \(x_1^* > 0\), \(y_1^* > 0\), \(x_2^* > 0\) et \(y_2^* > 0\) \[\lambda^* = c \left ( \frac{a_1-a_2}{b}-1 \right )-m,\] \[x_1^*=\frac{a_1}{a_1-a_2} \left [ 1 - \frac{b}{a_1-a_2} - \frac{a_2 b^2}{c(a_1-a_2)^2} \right ] ,\quad y_1^*=\frac{c}{b}-\frac{c}{a_1-a_2} - \frac{a_2 b}{(a_1-a_2)^2}\, ,\] \[x_2^* =\frac{a_2}{a_1-a_2} \left [ \frac{b}{a_1-a_2} - 1+ \frac{a_1 b^2}{c(a_1-a_2)^2} \right ] ,\quad y_2^*=\frac{c}{a_1-a_2}-\frac{c}{b}+ \frac{a_1 b}{(a_1-a_2)^2}\, .\]

    Preuve. Pour la première solution, \[(x_1,y_1)\neq (0,0),\quad (\lambda+m)\, x_1 = a_1 y_1- c\, x_1,\quad (\lambda+m)\, y_1 = c\, x_1.\] D'où l'équation quadratique pour λ \[(\lambda+m) (c+\lambda+m)- a_1 c=0.\] Les deux racines sont \[ \frac{ -c\pm \sqrt{c^2+4a_1 c} }{2}-m\] mais seule celle avec un + conduit à des solutions positives \((x_1,y_1)\).

    La deuxième solution s'obtient de la même manière en remplaçant l'indice 1 par l'indice 2.

    Pour la troisième solution, \begin{eqnarray} (\lambda+m) x_1 &=& a_1 \, y_1 - c\, x_1\, ,\quad (\lambda+m) y_1 = c\, x_1 - b\, \frac{y_1\, y_2}{y_1+y_2}\, ,\tag{4}\\ (\lambda+m) x_2 &=& a_2 \, y_2 - c\, x_2\, ,\quad (\lambda+m) y_2 = c\, x_2 + b \, \frac{y_1\, y_2}{y_1+y_2}\, .\tag{5} \end{eqnarray} On ne peut pas avoir \(c+\lambda+m=0\) car sinon \(y_1=0\). On a donc \(\,x_1=a_1 y_1/(c+\lambda+m)\) et \(x_2=a_2 y_2/(c+\lambda+m)\). D'où, en remplaçant dans les deux autres équations et en divisant par \(\,y_1\) ou \(y_2\), \[ \lambda+m = c \, \frac{a_1}{c+\lambda+m} - b\, \frac{y_2}{y_1+y_2}\, ,\quad \lambda+m = c \, \frac{a_2}{c+\lambda+m} + b\, \frac{y_1}{y_1+y_2}\, . \] En soustrayant ces deux équations, on obtient \begin{equation} \lambda = c \left ( \frac{a_1-a_2}{b}-1 \right )-m\, ,\quad \frac{y_1}{y_2} = \frac{1}{\frac{a_1}{a_1-a_2}+\frac{c}{b}-c\, \frac{a_1-a_2}{b^2}}-1:=\frac{1}{Q}-1\, .\tag{6} \end{equation} Le membre de droite dans la formule pour \(y_1/y_2\,\) doit être strictement positif. On a \[\frac{1}{Q}-1 \mathop{\longrightarrow}_{b\to 0^+} -1,\quad \quad \frac{1}{Q}-1 \mathop{\longrightarrow}_{b\to +\infty} -\frac{a_2}{a_1} < 0,\] et \[\frac{dQ}{db}=-\frac{c}{b^2} +\frac{2c(a_1-a_2)}{b^3}.\] On définit \(b_3=2(a_1-a_2)\). On a \[\frac{dQ}{db}(b) > 0\quad \forall b \in ]0,b_3[,\quad \quad \frac{dQ}{db}(b_3) = 0,\quad \quad \frac{dQ}{db} < 0\quad \forall b > b_3.\] Par ailleurs, un petit calcul montre que \(Q(b_1)=0\) et \(Q(b_2)=1\). On a aussi \(\,b_1 < b_2 < b_3\). On en conclut que

• sur l'intervalle \(]0,b_1[\), \(1/Q-1\) est une fonction décroissante qui décroît de −1 à −∞,
• sur l'intervalle \(]b_1,b_2[\), \(1/Q-1\) est une fonction décroissante qui décroît de +∞ à 0,
• sur l'intervalle \(]b_2,b_3[\), \(1/Q-1\) est encore une fonction décroissante et \(1/Q-1<0\),
• sur l'intervalle \(]b_3,+\infty[\) \(1/Q-1\) est une fonction croissante et on a encore \(1/Q-1<0\).

    Remarquons que \(b_1 < b_2\). Le taux de croissance \(\,\lambda^*\) donné par (6) décroît de \(\lambda_1\) jusqu'à \(\lambda_2\) sur l'intervalle \(b_1 < b < b_2\).

    Lorsque c converge vers +∞, le modèle avec deux groupes d'âges se réduit au modèle dans l'introduction avec un seul groupe d'âges. On constate bien que les deux seuils \(\,b_1\) et \(b_2\) convergent alors vers un seuil unique égal à \(a_1-a_2\).

3     La stabilité des solutions exponentielles

    Avec \(i\in \{1,2\}\), on définit \[{\cal X}_i=\frac{X_i}{X_1+Y_1+X_2+Y_2},\quad {\cal Y}_i=\frac{Y_i}{X_1+Y_1+X_2+Y_2}\, .\] On a \(\,{\cal X}_1+{\cal Y}_1+{\cal X}_2+{\cal Y}_2=1\). Un calcul assez simple à partir du système (1)-(2) donne \begin{eqnarray} \frac{d{\cal X}_1}{dt} &=& a_1 {\cal Y}_1 - c {\cal X}_1 - {\cal X}_1 \left [a_1 {\cal Y}_1 + a_2 {\cal Y}_2 \right ]\, ,\tag{7}\\ \frac{d{\cal Y}_1}{dt} &=& c {\cal X}_1 - b\, \frac{{\cal Y}_1\, {\cal Y}_2}{{\cal Y}_1+{\cal Y}_2}- {\cal Y}_1 \left [a_1 {\cal Y}_1 + a_2 {\cal Y}_2 \right ]\, ,\tag{8}\\ \frac{d{\cal X}_2}{dt} &=& a_2\, {\cal Y}_2 - c\, {\cal X}_2- {\cal X}_2 \left [a_1 {\cal Y}_1 + a_2 {\cal Y}_2 \right ]\, ,\tag{9}\\ \frac{d{\cal Y}_2}{dt} &=& c\, {\cal X}_2 + b\, \frac{{\cal Y}_1\, {\cal Y}_2}{{\cal Y}_1+{\cal Y}_2}- {\cal Y}_2 \left [a_1 {\cal Y}_1 + a_2 {\cal Y}_2 \right ] .\tag{10} \end{eqnarray}

    Soit une solution exponentielle normalisée du système (1)-(2), \(e^{\lambda t} z\) avec \(z=(x_1,y_1,x_2,y_2)\). On a les équations (4)-(5). En additionnant les quatre équations, on obtient \[a_1 y_1+a_2 y_2=\lambda+m.\] On en déduit que z est un point d'équilibre du système (7)-(10). On dit que la solution \(\,e^{\lambda t} z\ \) est « asymptotiquement stable » (respectivement instable) si z est un point d'équilibre asymptotiquement stable (resp. instable) du système (7)-(10). Il résulte du théorème d'Euler pour les fonctions homogènes vectorielles (ici de degré un) que λ est toujours une valeur propre de la matrice jacobienne de la fonction F définie par (3) au point z : \(J_F(z)\). En effet, \[J_F(z) z=F(z)=\lambda\, z.\] D'après [6, p. 638], le point d'équilibre z est asymptotiquement stable si les trois valeurs propres de cette matrice jacobienne, autres que λ, ont une partie réelle strictement inférieure à λ. Le point d'équilibre est instable si l'une de ces trois valeurs propres a une partie réelle strictement supérieure à λ. C'est ce que l'on va utiliser dans la proposition suivante.

Proposition 2

• La solution exponentielle normalisée de la proposition 1, \(\,e^{\lambda_1 t} (x_1,y_1,0,0)\,\), est asymptotiquement stable si \(b < b_1\), instable si \(b > b_1\).
• La solution exponentielle normalisée de la proposition 1, \(\,e^{\lambda_2 t} (0,0,x_2,y_2)\,\), est asymptotiquement stable si \(b > b_2\), instable si \(b < b_2\).
• La solution exponentielle normalisée de la proposition 1, \(\,e^{\lambda^* t} (x_1^*,y_1^*,x_2^*,y_2^*)\,\), est asymptotiquement stable pour \(b_1 < b < b_2\).

    Preuve. De manière générale, si \(\,z=(x_1,y_1,x_2,y_2)\) avec \(y_1+y_2 > 0\) et si \(p=y_2/(y_1+y_2)\), on a alors \begin{equation} J_F(z) = \left (\begin{array}{cccc} -c-m & a_1 & 0 & 0\\ c &-b\, p^2-m & 0 & - b (1-p)^2\\ 0 & 0 & -c-m & a_2\\ 0 & b\, p^2 & c & b (1-p)^2-m \end{array} \right ).\tag{11} \end{equation}

    Dans le premier cas, on a p=0, donc \[ J_F(z)=\left (\begin{array}{cc|cc} -c-m & a_1 & 0 & 0\\ c & -m & 0 & -b \\ \hline 0 & 0& -c-m & a_2\\ 0 & 0 & c & b-m \end{array} \right ).\] La plus grande valeur propre du bloc supérieur gauche est \(\lambda_1\). La plus grande valeur propre du bloc inférieur droit est \[\mu_2= \frac{ b-c+\sqrt{(b+c)^2+4a_2c}}{2}-m.\] C'est une fonction croissante de b. Après quelques calculs, on obtient \(\,\mu_2 > \lambda_1\) si \(b > b_1\) et \(\mu_2 < \lambda_1\) si \(b < b_1\).

    Dans le deuxième cas, on a p=1, donc \[ J_F(z)= \left (\begin{array}{cc|cc} -c-m & a_1 & 0 & 0\\ c & -b-m & 0 & 0 \\ \hline 0 & 0& -c-m & a_2\\ 0 & b & c & -m \end{array} \right ) .\] La plus grande valeur propre du bloc inférieur droit est \(\lambda_2\). La plus grande valeur propre du bloc supérieur gauche est \[\mu_1= \frac{ -b-c+\sqrt{(b-c)^2+4a_1c}}{2}-m.\] C'est une fonction décroissante de b parce que \[2 \, \frac{d\mu_1}{db} = -1+ \frac{b-c}{\sqrt{(b-c)^2+4a_1c}} < 0.\] Après quelques calculs, on obtient \(\,\mu_1 > \lambda_2\) si \(b < b_2\) et \(\mu_1 < \lambda_2\) si \(b > b_2\).

    Dans le troisième cas, on a \(0 < p < 1\). Il résulte alors de l'équation (6) que \[p = \frac{y_2^*}{y_1^* + y_2^*}= \frac{a_1}{a_1 - a_2} + \frac{c}{b} - c\, \frac{a_1 - a_2}{b^2}\, .\] On sait déjà que \(\lambda^*\) est une valeur propre de la matrice \(J_F(z)\,\) définie par (11). La question est de savoir si les trois autres valeurs propres ont une partie réelle strictement inférieure à \(\,\lambda^*\). Autrement dit, la matrice \(\,M=J_F(z)-\lambda^* I\) a une valeur propre nulle et il s'agit de savoir si les autres valeurs propres ont une partie réelle strictement négative. On a \[ M=\left ( \begin{array}{cccc} -c\frac{a_1-a_2}{b} & a_1 & 0 & 0 \\ c & -bp^2-c\frac{a_1-a_2}{b}+c & 0 & -b(1-p)^2\\ 0 & 0 & -c\frac{a_1-a_2}{b} & a_2 \\ 0 & b p^2 & c & b(1-p)^2-c\frac{a_1-a_2}{b}+c \end{array} \right ).\] Le polynôme caractéristique est donc de la forme \[ \chi(\xi)=\mathrm{d\acute{e}t}(M-\xi I)=\xi(\xi^3+k_2 \xi^2 + k_1 \xi + k_0).\] Avec un développement selon la première colonne, on trouve \begin{eqnarray*} \chi(\xi)&= &- \left [c\frac{a_1-a_2}{b}+\xi \right ] \Biggl \{ \left [bp^2+c\frac{a_1-a_2}{b}-c+\xi \right ] \left [ c\frac{a_1-a_2}{b} +\xi \right ] \left [b(1-p)^2-c\frac{a_1-a_2}{b}+c-\xi \right ]\\ &&\quad \quad \quad \quad \quad \quad \quad \quad -b^2 p^2 (1-p)^2 \left [ c \frac{a_1-a_2}{b} +\xi \right ] +a_2 c \left [bp^2+c\frac{a_1-a_2}{b}-c+\xi \right ] \Biggr \} \\ &&-c \Biggl \{ - a_1 \left [ c \frac{a_1-a_2}{b} +\xi \right ] \left [b(1-p)^2-c\frac{a_1-a_2}{b}+c-\xi \right ] -a_1 a_2 c \Biggr \}. \end{eqnarray*} Pour le coefficient de \(\xi^3\), on trouve \[k_2=4c \frac{a_1-a_2}{b} -2c -b (1-2p),\] et après simplification \[k_2= \frac{(a_1+a_2) b^2+2(a_1-a_2)^2 c}{(a_1-a_2)b}.\] Pour le coefficient de \(\xi^2\), on trouve \begin{eqnarray*} k_1 &= & \left [ -3 c \frac{a_1-a_2}{b} - bp^2+c\right ] \left [b(1-p)^2-c\frac{a_1-a_2}{b}+c \right ] + c^2 \frac{(a_1-a_2)^2}{b^2} \\ & &+ 2 c\frac{a_1-a_2}{b} \left [bp^2+c\frac{a_1-a_2}{b}-c \right ] + b^2 p^2 (1-p)^2 -a_1 c - a_2 c, \end{eqnarray*} et après une simplification laborieuse \[k_1= c \, \frac{[2(a_1-a_2)-b] [ (a_1+a_2)b+(a_1-a_2)c ]}{(a_1-a_2)b}.\] Enfin, pour le coefficient de ξ, on a utilisé le logiciel de calcul formel Xcas (https://www.xcasenligne.fr) pour obtenir \[k_0 =-c\, \frac{[a_1b^2+(a_1-a_2)bc-(a_1-a_2)^2c] [a_2b^2+(a_1-a_2)bc-(a_1-a_2)^2c]}{(a_1-a_2)b^3}.\] \(k_0\) peut aussi s'écrire sous la forme \begin{eqnarray*} k_0 &=& - k (b-b_1)(b-b_2) \, , \\ k &=& \frac{a_1 a_2 c}{b^3 (a_1-a_2)} \left (b+\frac{2(a_1-a_2)}{\sqrt{1+4a_1/c}-1} \right )\left (b+\frac{2(a_1-a_2)}{\sqrt{1+4a_2/c}-1} \right )\, . \end{eqnarray*} Pour que les trois racines du polynôme \(\xi^3+k_2 \xi^2 + k_1 \xi + k_0\) aient une partie réelle strictement négative, il faut et il suffit d'après le critère de Routh-Hurwitz que \(k_2 > 0\), \(k_1 > 0\), \(k_0 > 0\) et \(k_1 k_2-k_0 > 0\) [17, p. 134]. On a \(\,k_2 > 0\). D'autre part, \(k_1 > 0\) si \(0 < b < 2(a_1-a_2)\) et donc en particulier pour \(b_1 < b < b_2\) parce que \(b_2 < a_1-a_2\). On a aussi \(\,k_0 > 0\) si \(b_1 < b < b_2\). Il ne reste donc qu'à prouver que \(\,k_1 k_2-k_0 > 0\) si \(b_1 < b < b_2\). En développant le produit \(\,k_1k_2\,\) et en rangeant le numérateur comme un polynôme en la variable b, on obtient \begin{eqnarray*} k_1k_2-k_0&=& \Bigl \{ (a_1-a_2)^5 c^2 +2(a_1-a_2)^4 c^2 b\\ &&+\bigl [-(a_1-a_2)^3 c^2 + 3(a_1+a_2)(a_1-a_2)^3 c\bigr ]\, b^2\\ &&+(a_1-a_2)^2(a_1+a_2)c\, b^3\\ &&+\bigl [-(a_1-a_2)(a_1+a_2)c+a_1a_2(a_1-a_2)+2(a_1+a_2)^2(a_1-a_2)\bigr ] b^4\\ &&-(a_1+a_2)^2 b^5 \Bigr \} \frac{c}{(a_1-a_2)^2 b^3}. \end{eqnarray*} On regroupe certaines parties : \begin{eqnarray*} k_1k_2-k_0&=& \Bigl \{ (a_1-a_2)^5 c^2 +(a_1-a_2)^3 c^2 b \bigl [2(a_1-a_2)-b\bigr ]\\ &&+ 3(a_1+a_2)(a_1-a_2)^3 c\, b^2 +(a_1^2-a_2^2)c\, b^3 \bigl [(a_1-a_2)-b\bigr ]\\ &&+a_1a_2(a_1-a_2) b^4 +(a_1+a_2)^2 b^4 \bigl [2(a_1-a_2)-b\bigr ] \Bigr \} \frac{c}{(a_1-a_2)^2 b^3}. \end{eqnarray*} Les termes entre crochets sont tous strictement positifs parce que \(\,b < b_2 < a_1-a_2\). On a ainsi \(\,k_1 k_2 - k_0 > 0\). La troisième solution est donc bien asymptotiquement stable pour \(\,b_1 < b < b_2\).

4     Exemple

    Prenons \(a_1=10\%\,\) par an. Rappelons que ce paramètre est égal au nombre de naissances dans les familles avec une fécondité élevée divisé par la population adulte avec une fécondité élevée, et non le taux de natalité employé habituellement en démographie, qui divise par la population totale. Prenons aussi : \(a_2=4\%\) par an, \(c=5\%\) par an, de sorte que \(1/c=20\) ans, et \(m=2\%\,\) par an. L'espérance de vie à la naissance est donc \(\,1/m=50\,\) ans. Rappelons qu'en 2017, les espérances de vie pour les hommes et pour les femmes étaient par exemple égales à 52 et 55 ans en Côte d'Ivoire, à 51 et 54 ans au Tchad, à 50 et 53 ans en Centrafique [15].

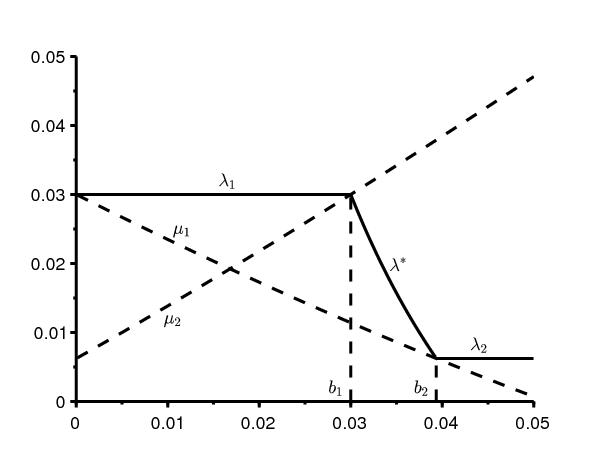
    Avec ces valeurs des paramètres, on obtient \(\lambda_1=3\%\) par an et \(\lambda_2\simeq \mbox{0,62}\%\) par an, \(b_1= 3\%\) par an et \(b_2\simeq 3,9\%\,\) par an. La figure 1 montre les différents taux de croissance \(\lambda_1\), \(\lambda^*\) et \(\lambda_2\,\) en fonction de b. On a une transition démographique partielle si \(\,b_1 < b < b_2\,\), avec un taux de croissance \(\lambda^*\). Par comparaison, le taux d'accroissement naturel est de 2,4% en Côte d'Ivoire, de 3,3% au Tchad et de 2,2% en Centrafique. Le Tchad serait donc plutôt dans le cas où \(\,b < b_1\), tandis que les deux autres pays seraient dans la situation intermédiaire avec \(b_1 < b < b_2\).

    Pour ce modèle, on peut calculer la proportion de « jeunes » dans la population. Cette proportion est \[x_1/(x_1+y_1)=1/(1+c/(\lambda_1+m))=50\%\] si \(\,b < b_1\). Cette proportion est \[x_2/(x_2+y_2)=1/(1+c/(\lambda_2+m))\simeq 34\%\] si \(b > b_2\). Néanmoins, étant donnée la structure du modèle, ces « jeunes » auraient une moyenne d'âge \(\,1/(c+m)\simeq \mbox{14,3}\,\) ans. Il est donc difficile de comparer avec les statistiques démographiques. D'après [15], la proportion des moins de 15 ans est de 43% en Côte d'Ivoire, de 48% au Tchad et de 44% en Centrafique.

    Le taux de natalité est

• \(a_1 y_1/(x_1+y_1)=a_1 c/(\lambda_1+m+c)=50\) pour 1000 habitants si \(b < b_1\),
• \(a_2 y_2/(x_2+y_2)=a_2 c/(\lambda_2+m+c)=26\) pour 1000 habitants si \(b > b_2\).

    Ainsi donc, les valeurs choisies pour les paramètres ne sont pas trop irréalistes.

5     Le comportement asymptotique

    L'étude de stabilité n'était jusqu'ici que locale. Le système est de dimension 4 et se ramène au mieux à un système de dimension 3. Il ne semble pas possible d'utiliser le théorème de Poincaré-Bendixson pour déterminer le comportement asymptotique global. Dans le modèle démographique avec des mariages de [16, chap. 4], le système était de dimension deux.

    Il est également difficile de trouver une fonction de Liapounov convenable. Notre système homogène peut certes se transformer en un système avec uniquement des termes linéaires ou quadratiques si l'on prend comme nouvelles inconnues \(\,X_1/(Y_1+Y_2)\), \(Y_1/(Y_1+Y_2)\), \(X_2/(Y_1+Y_2)\) et \(Y_2/(Y_1+Y_2)\). Mais la fonction de Liapounov avec des termes logarithmiques utilisée par exemple par [2] pour une classe particulière de pareils systèmes ne semble pas convenir.

    En s'inspirant du modèle linéaire de population de [4, p. 80], on obtient cependant la proposition suivante.

Proposition 3. La fonction \[V(t)=\frac{1}{2} [e^{-\lambda_1 t} X_1(t)]^2 +\frac{1}{2} \frac{a_1}{c} [e^{-\lambda_1 t} Y_1(t)]^2\] est toujours positive et décroissante.

    Preuve. On définit plus généralement \(\,V(t)=\frac{1}{2} [e^{-\lambda t} X_1(t)]^2 +\frac{1}{2} k [e^{-\lambda t} Y_1(t)]^2\) avec \(k > 0\). On a alors \begin{eqnarray*} \frac{dV}{dt}&=&e^{-2\lambda t} X_1 [-\lambda X_1 + a_1 Y_1 -(c+m)X_1] \\ &&+ k\, e^{-2\lambda t} Y_1 \left [-\lambda Y_1 +c X_1 - mY_1 - b \frac{Y_1Y_2}{Y_1+Y_2}\right ]\, . \end{eqnarray*} \(Y_1(t) > 0\) et \(Y_2(t) > 0\). Le terme avec b en facteur est donc négatif \begin{eqnarray*} \frac{dV}{dt}&\leq& e^{-2\lambda t} \left [ (-\lambda-c-m) X_1^2 + (a_1+kc) X_1 Y_1 -(\lambda+m)k\, Y_1^2\right ]. \end{eqnarray*} Pourvu que \(\lambda+c+m\neq 0\), on obtient \begin{eqnarray*} \frac{dV}{dt}&\leq& e^{-2\lambda t} \Biggl \{-(\lambda+c+m) \left [X_1-\frac{a_1+kc}{2(\lambda+c+m)} Y_1 \right ]^2\\ & & \quad \quad \quad + \left [ \frac{(a_1+kc)^2}{4(\lambda+c+m)} -(\lambda+m)k \right ] Y_1^2\Biggr \}. \end{eqnarray*} Le coefficient de \(Y_1^2\) est égal à 0 si on choisit \[\lambda=\frac{-c \pm \sqrt{c^2+2a_1 c +a_1^2/k + kc^2}}{2}-m.\] On ne conserve que la racine avec un + dans \(\pm\), de sorte que \(\lambda+c+m > 0\). Cette racine, qui dépend de k, est minimale si \(\,a_1^2/k + kc^2\) est minimum, c'est-à-dire si \(k=a_1/c\). Avec ce choix, on a \(\lambda=\lambda_1\) et \begin{eqnarray*} \frac{dV}{dt}&\leq& - e^{-2\lambda_1 t} \, \frac{c+\sqrt{c^2+4a_1c}}{2}\, \left [X_1 - \frac{\lambda_1+m}{c}\, Y_1\right ]^2 \leq 0. \end{eqnarray*}

    \(V(t)\,\) converge vers une limite ≥0. En particulier, il existe une constante \(\,K > 0\) avec \(\forall \, t > 0, \ X_1(t)\leq K\, e^{\lambda_1 t}\) et \(Y_1(t)\leq K\, e^{\lambda_1 t}\).

Proposition 4. La fonction \[W(t)=\frac{1}{2} [e^{-\lambda t} X_2(t)]^2 +\frac{1}{2} \frac{a_2}{c} [e^{-\lambda t} Y_2(t)]^2\] avec \begin{equation} \lambda=\frac{b-c+\sqrt{(b+c)^2+4a_2 c}}{2}-m \tag{12} \end{equation} est toujours positive et décroissante.

    Preuve. On définit plus généralement \(\,W(t)=\frac{1}{2} [e^{-\lambda t} X_2(t)]^2 +\frac{1}{2} k [e^{-\lambda t} Y_2(t)]^2\) avec \(k > 0\). On a alors \begin{eqnarray*} \frac{dW}{dt}&=&e^{-2\lambda t} X_2 [-\lambda X_2 + a_2 Y_2 -(c+m)X_2] \\ &&+ k\, e^{-2\lambda t} Y_2 \left [-\lambda Y_2 +c X_2 - mY_2 + b \frac{Y_1Y_2}{Y_1+Y_2}\right ]\, . \end{eqnarray*} Avec \(Y_1/(Y_1+Y_2)\leq 1\) \begin{eqnarray*} \frac{dW}{dt}&\leq &e^{-2\lambda t} \left [ -(\lambda+c+m) X_2^2 +(a_2 + k c) X_2 Y_2 + k (b-\lambda-m) Y_2^2 \right ]. \end{eqnarray*} Pourvu que \(\lambda+c+m\neq 0\,\), on a \begin{eqnarray*} \frac{dW}{dt}&\leq &e^{-2\lambda t} \Biggl \{ -(\lambda+c+m) \left [ X_2 - \frac{a_2+kc}{2(\lambda+c+m)} Y_2 \right ]^2 \\ &&\quad \quad \quad + \left [ k (b-\lambda-m) + \frac{(a_2+kc)^2}{4(\lambda+c+m)}\right ] Y_2^2 \Biggr \}. \end{eqnarray*} Le coefficient de \(Y_2^2\) est égal à 0 si on choisit \[\lambda=\frac{b-c \pm \sqrt{(b+c)^2+2a_2 c +a_2^2/k + kc^2}}{2}-m.\] On ne conserve que la racine avec un + dans \(\pm\), de sorte que \(\lambda+c+m > 0\). Cette racine, qui dépend de k, est minimale si \(\,a_2^2/k + kc^2\) est minimum, c'est-à-dire si \(k=a_2/c\). Alors λ est donné par la formule (12) et on a \(\,dW/dt \leq 0\).

    Ces résultats ne permettent pas néanmoins de distinguer les différents régimes selon la valeur de b. On conjecture que :

• si \(b < b_1\), on a \[e^{-\lambda_1 t } (X_1,Y_1,X_2,Y_2) \mathop{\longrightarrow}_{t\to +\infty} (x_1,y_1,0,0)\] avec \(x_1 > 0\), \(y_1 > 0\) et \((\lambda_1+m) y_1=c\, x_1\). C'est la population avec une fécondité élevée qui en proportion finit par dominer.
• si \(b_1 < b < b_2\), on a \[e^{-\lambda^* t } (X_1,Y_1,X_2,Y_2) \mathop{\longrightarrow}_{t\to +\infty} (x_1,y_1,x_2,y_2)\] et il existe une constante \(\alpha > 0\) avec \((x_1,y_1,x_2,y_2)=\alpha (x_1^*,y_1^*,x_2^*,y_2^*)\), ce dernier vecteur étant celui de la proposition 1. Il y a coexistence dans les proportions des sous-populations avec des fécondités différentes ;
• si \(b > b_2\), on a \[e^{-\lambda_2 t } (X_1,Y_1,X_2,Y_2) \mathop{\longrightarrow}_{t\to +\infty} (0,0,x_2,y_2)\] avec \(x_2 > 0\), \(y_2 > 0\) et \((\lambda_2+m) y_2 = c\, x_2\). C'est la population avec une fécondité basse qui en proportion finit par dominer.

    Ainsi donc, la transition démographique partielle observée dans certains pays d'Afrique subsaharienne pourrait correspondre au cas intermédiaire où \(b_1 < b < b_2\).

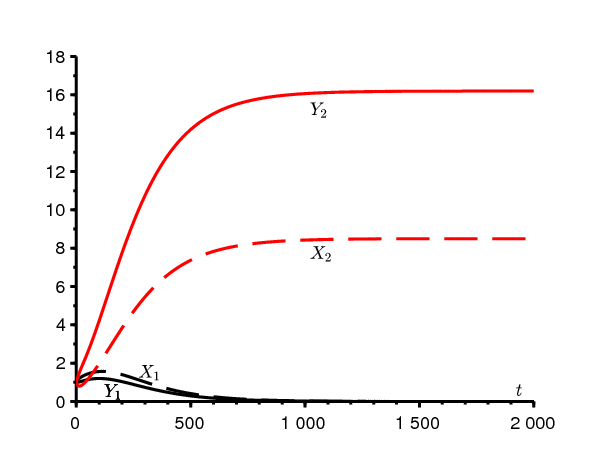
    Pour soutenir cette conjecture, considérons l'exemple numérique de la section précédente. Prenons une condition initiale quelconque, par exemple \(\,X_1(0)=Y_1(0)=X_2(0)=Y_2(0)=1\,\) (comme le système est homogène, on peut penser à 1 million). La figure 2 montre comment le système se comporte selon la position de b par rapport aux deux seuils. Si la conjecture semble bien se confirmer, on notera cependant dans le cas où \(\,b_1 < b < b_2\,\) que le temps caractéristique de convergence est assez long. La deuxième valeur propre de la matrice jacobienne \(\,J_F(z)\) est proche de \(\lambda^*\).

Références bibliographiques